叶轮出口环量非线性分布条件下混流泵性能研究
王梦成 李彦军 袁建平 陈加琦 郑云浩 杨平辉
(1.江苏大学国家水泵及系统工程技术研究中心, 镇江 212013; 2.武汉特种工业泵厂有限公司, 武汉 430058)
0 引言
混流泵性能介于轴流泵与离心泵之间,具有良好的综合性能,被广泛应用于工农业领域。然而,相比于离心泵,混流泵设计理论体系尚不成熟[1-2]。目前,关于混流泵的设计优化方法主要有两种,分别为正问题设计(以叶片几何参数作为设计参数)和反问题设计(以叶片载荷或压力作为设计参数)[3]。相比正问题设计,反问题设计的设计参数与水力性能联系更为紧密,其有效性已在各种涡轮机械的设计优化中得到证明[4-8]。

为研究叶轮出口翼展方向环量分布形式对混流泵性能的影响,本文以应用于南水北调东线工程中比转数为510的混流泵叶轮为基础模型,在不改变其轴面投影图和叶片厚度分布规律的基础上,保持流线方向载荷控制参数不变,对比分析17种不同翼展方向环量分布形式对混流泵外特性及内流场的影响规律,以期为混流泵的反问题设计提供参考。
1 反问题设计
1.1 反问题设计理论基础
全三维反问题设计最早由文献[16-17]提出,文献[18-20]基于势流理论对其进行了进一步发展,并通过引入阻塞因子提出了一种考虑粘性作用的全三维反问题设计方法。本文研究采用ZANGENEH[18,20]提出的全三维反问题设计方法。
在该方法中,假定流体定常、无粘、不可压缩,叶片形状满足叶片微分方程
(1)
式中f——包角m——沿轴面流线位移
ω——叶轮旋转角速度
Vm——轴面相对速度
叶轮中流体速度可分解为周向平均速度与周期脉动速度,公式为
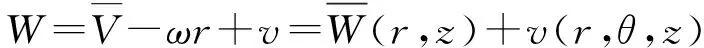
(2)
式中W——相对速度
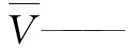

v——周期速度
θ、z——圆柱坐标系切向、轴向坐标值
对于不可压缩流体,考虑到叶片的阻塞效应,周向平均绝对速度满足方程
(3)

(4)
式中Bf——阻塞因子
tθ——叶片切向厚度
B——叶片数
根据式(3),定义流函数Ψ(r,z)满足条件
(5)

(6)
式中α——叶片角
周向平均涡量的切向分量为
(7)
将式(5)、(6)代入式(7)得
(8)
式(8)的求解需要壁面与上下游边界条件,在壁面处,流函数为定值,上下游边界条件由给出的平均速度条件确定,满足
(9)
式中s——沿上下游边界的距离

式(8)结合边界条件即可求解出周向平均绝对速度。
根据Clebsh公式,周期速度可被分解为势流部分与旋转部分,即
(10)

(11)
式中φ(r,θ,z)——周期速度的势函数
S(α)——周期脉动函数
将式(10)、(11)代入连续性方程可得
(12)
由于流动具有周期性特征,因此势函数φ(r,θ,z)可以在切向进行傅里叶级数展开,即
(13)
将式(13)代入式(12)可得
(14)
通过引入上下游处周期速度为零和壁面处周期速度法向矢量为零的向量,即可由式(14)求解出周期速度。
叶片形状由叶片处不可穿透条件和无滑移条件确定,即
(15)
式中Wbl——轴面相对速度

O——零向量
结合式(2),可将式(15)展开为
(16)
式中vzbl、vrbl、vθbl——轴向、径向、周向周期速度分量
式(1)、(8)、(14)、(16)共同构成反问题设计控制方程组,在此基础上给定约束条件(设计参数),即可通过迭代计算得到对应的叶片形状。
1.2 反问题设计流程
本文原始模型为南水北调工程中比转数为510的混流泵,其额定流量Q=420.7 kg/s,额定扬程H=12.6 m,额定转速n=1 450 r/min,叶片数B=4,直径D=320 mm。反问题设计中,需要给定条件如下:
(1)轴面投影图:轴面投影图由轮毂、轮缘和叶片进口边与出口边组成,由水力计算确定。本研究为探究翼展环量分布形式对混流泵性能的影响,对原始模型轴面投影图不作任何更改。
(2)叶片厚度分布:保持与原始模型相同的叶片厚度分布。
(3)额定转速与额定流量:保持额定转速、额定流量与原始模型一致。
(4)进、出口边翼展方向环量分布:与初始模型类似,假定叶轮进口边环量为零。出口边环量由叶轮设计点扬程决定,分布形式由控制点处环量确定。

(17)
式中p+——叶片压力面静压
p-——叶片吸力面静压
ρ——流体密度


图1 轴面流线方向载荷分布Fig.1 Loading distribution along meridional streamlines
2 CFD数值模拟及准确性验证
2.1 计算设置
采用商业软件CFX对计算域进行数值计算。文中所有计算均采用SSTk-ω湍流模型,其有效地综合了k-ω模型在近壁面处计算优点与k-ε模型在湍流充分发展区计算优点;泵段进口与出口分别采用总压进口与质量流量出口条件;旋转域与静止域之间的交界面采用冻结转子条件;对流项求解采用高精度模式;对于旋转机械,综合考虑计算收敛性与计算资源消耗,时间步长选定为1/ω;收敛精度设置为10-5。
2.2 模型建立及网格无关性计算
计算域由进水直管、叶轮、导叶和出水弯管组成,如图2所示。使用结构化网格对计算域进行离散,并对壁面处进行加密处理,其中进水管道与出水管道网格划分使用ICEM完成,叶轮与导叶网格划分使用Turbogrid完成,如图3所示。

图2 计算域Fig.2 Calculation field1.进水直管 2.叶轮 3.导叶 4.出水弯管

图3 各部件网格图Fig.3 Meshes for different parts
综合考虑各部件网格数对计算结果的影响,设计了9种不同网格数组合,如表1所示。以泵段效率和扬程作为外特性网格无关性检测标准,叶轮出

表1 网格数Tab.1 Grid number
口边翼展方向轴向速度与总压分布作为内流场网格无关性检测标准,计算结果如图4所示。由图可知,当网格数由460万增加到849万时,网格数对外特性和内流场计算结果基本无影响,综合考虑计算精度与计算资源消耗,最终选定网格数为460万。
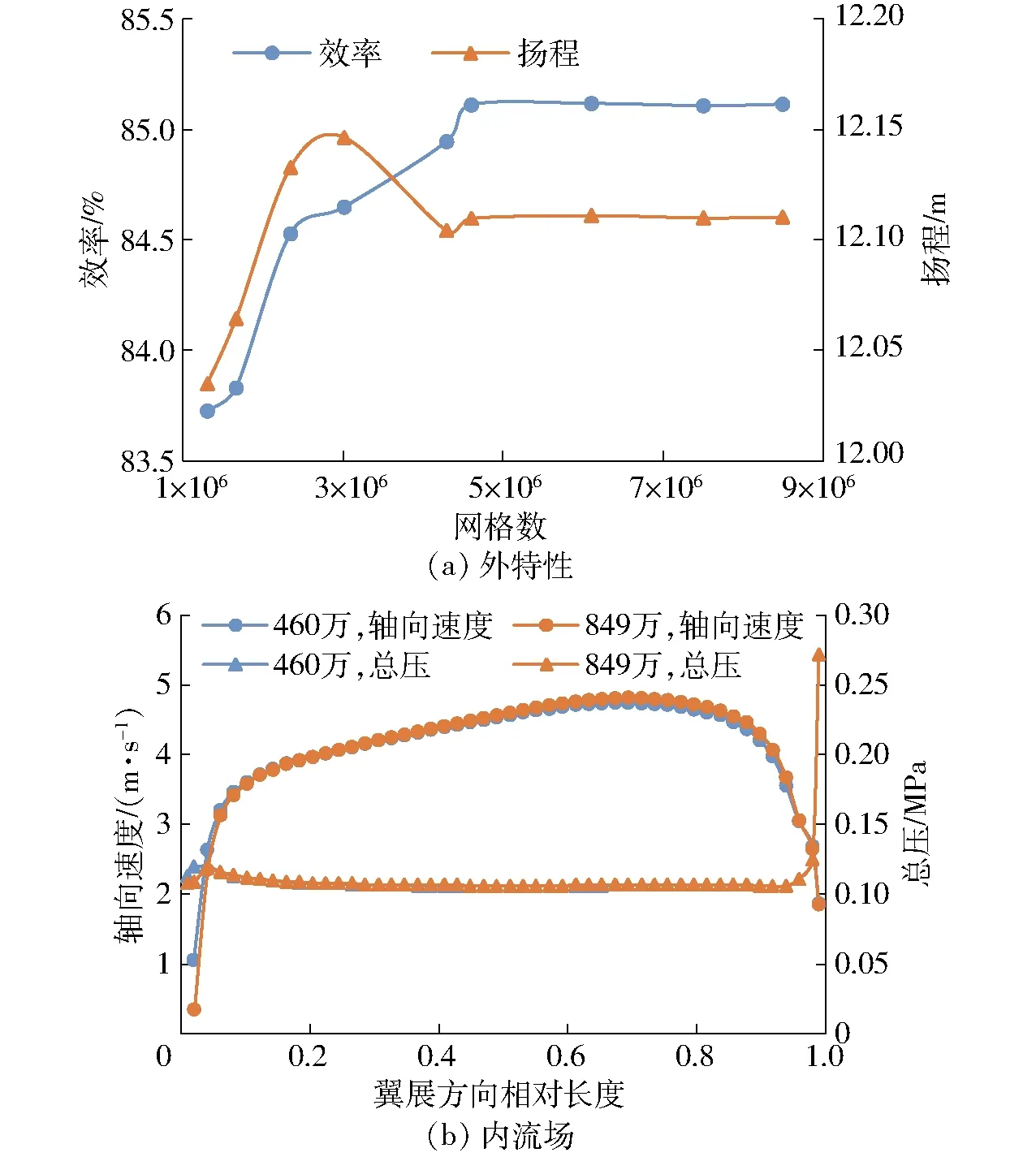
图4 网格无关性测试结果Fig.4 Result of mesh independence test
2.3 试验验证
原始模型试验由南水北调天津同台测试完成并在江苏大学试验台完成复核,两者结果吻合性良好。文中所有计算均采用2.1节所述计算设置与2.2节所述网格划分,将原始模型外特性计算结果与试验值进行对比并将原始模型与下文环量组合1(即各控制点取环量最大值与最小值之和的1/2)计算结果进行对比以确保下文数值模拟可行性,结果如图5所示。在整个流量范围内,原始模型试验值与模拟值变化趋势基本一致,最大误差不超过3%而环量组合1所对应混流泵与原始模型泵性能相近,因此本文所用数值模拟方法满足计算精度要求。

图5 模拟验证Fig.5 Simulation verification
3 翼展方向环量分布控制方法
在过往研究中,设计人员通过给定轮毂与轮缘处环量,其它位置线性插值的方法来确定翼展方向环量分布形式,其所有可能的分布形式只有3种,分别为均匀分布、递增分布与递减分布[24-25]。为详细探究翼展方向环量的分布形式与叶轮性能之间的关系,特别是各种非线性环量分布对叶轮性能的影响,本文通过自编文件增加控制点的方法控制翼展方向环量分布形式。由微积分概念可知,当增加的控制点足够多时,可以实现任意形式的环量分布,然而,所需计算量也随之急剧增加。综合考虑环量分布形式的多样性与所需计算量,最终确定控制点个数为5个,分别位于叶片出口边轮毂、25%翼展位置、50%翼展位置、75%翼展位置和轮缘处。
为便于表述,下文中使用展向相对位置代替展向位置,定义展向相对位置
(18)
式中ra——翼展方向无量纲化半径
rh——轮毂半径rs——轮缘半径
记轮毂到轮缘处5个控制点环量值分别为X1~X5,在反问题设计中,当翼展方向环量最大值与最小值相差较大时,叶片过度扭曲易造成计算失败,故对其施加约束条件
(19)

Xmax——控制点处环量最大值
Xmin——控制点处环量最小值
为使各环量分布形式具有对比性且性能差异更加明显,参照正交设计试验方法,将各控制点处环量设定为3个水平且满足方程
(20)
记Xmax为1,(Xmax+Xmin)/2为0,Xmin为-1。则所有具有代表性的环量分布组合如表2所示。
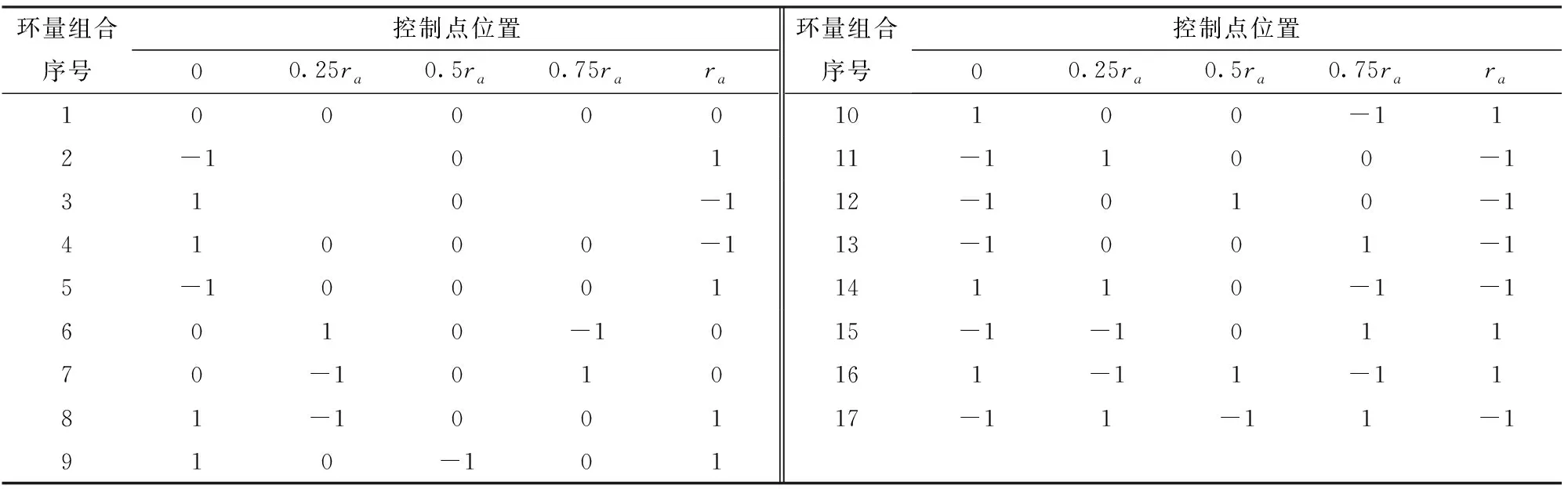
表2 环量分布形式Tab.2 Circulation distribution form

图6 代表性环量分布形式Fig.6 Typical circulation distribution forms

环量组合1对应叶片形状如图7a所示,环量组合1与环量组合2、3、5、12、17对应叶片对比图如图7b~7f所示,图7中所有灰色叶片均为环量组合1对应叶片。由图7可知,当流线方向载荷控制参数保持不变时,控制叶轮出口翼展方向环量分布形式可有效控制叶片形状,因此,研究翼展方向环量分布形式对混流泵性能的影响是有必要的。

图7 不同环量分布对应叶片形状Fig.7 Blade shapes for diffident circulation forms
4 环量分布形式对混流泵性能的影响分析
4.1 效率及扬程
混流泵优点之一为具有广阔的高效区,若只关注设计点性能与环量分布形式间的关系,则难以满足后续混流泵参数化设计要求,故取0.8Qdes、Qdes和1.2Qdes(Qdes表示设计流量)3个工况点处性能参数作为目标函数。
为使结果更加直观具有代表性,以被广泛采用的环量分布1作为参考,定义
(21)
(22)
式中H1——环量组合1对应的扬程
Hi——相同工况下环量组合i对应的扬程
ΔHi——扬程相对提升百分比
η1——环量组合1对应的效率
ηi——相同工况下环量组合i对应的效率
Δηi——效率相对提升百分比
计算结果如表3(表中ΔAi表示叶片空化面积相对提升百分比)所示。由表3可知,通过简单调整叶轮出口处翼展方向平均环量值,可在改变环量分布形式的前提下保持设计工况处叶轮扬程波动小于2%,此时,小流量工况处最大扬程波动为2.41%,大流量工况处最大扬程波动为5.96%。因此,在保持设计工况处扬程基本不变的前提下,通过控制出口处翼展方向环量分布形式,可对大流量工况处扬程进行微弱调整。
分析表3中小流量工况处效率改变规律可知,当环量分布形式改变时,小流量工况处效率基本不变。分析环量组合4、7、11、12、13、15、17可知,当轮缘处环量较小、0.75ra处环量较大时,大流量工况处效率有较大的提升,设计工况处效率有微弱的提升;对比环量组合7、11、13和15可知,相较于轮缘处环量,0.75ra处环量对大流量工况处效率提升起主导作用。
因此,在保持叶轮设计工况处扬程基本不变的前提下,环量分布形式对大流量工况叶轮效率和扬程具有较大影响,而对设计工况与小流量工况叶轮效率和扬程的影响较小。为进一步拓宽混流泵叶轮优化设计空间,考虑翼展方向环量非线性分布是有必要的,一种较为理想的环量分布形式是给予0.75ra处较大环量并给予轮缘处较小的环量。
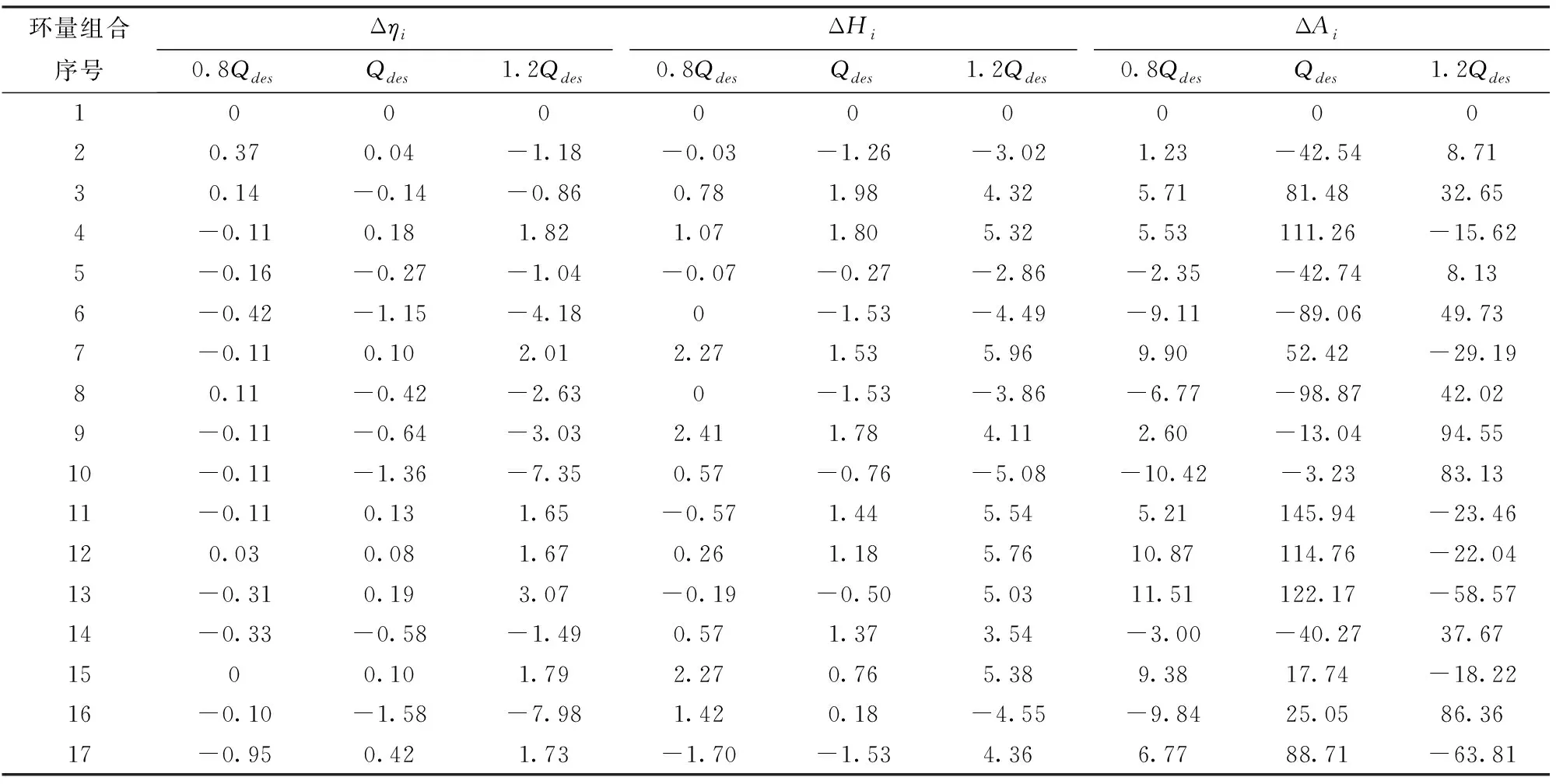
表3 环量分布对混流泵叶轮性能的影响Tab.3 Effect of circulation distribution on performance of mixed flow pump impeller %
4.2 空化性能
为节省计算时间,本文所有计算均采用单相流模型,假定叶片表面静压低于常温下水体所对应的气化压力处发生空化[26-27],则可以此面积作为叶片空化性能的判别标准。与4.1节类似,定义
(23)
式中A1——环量组合1对应的叶片空化面积
Ai——相同工况下环量组合i对应的叶片空化面积
计算结果如表3所示。由表可知当轮缘处环量较大,0.75ra处环量较小时,可有效提升小流量工况和设计工况处空化性能,但会降低大流量工况处空化性能,如环量组合5、6、8和10;当轮毂处与轮缘处环量较小,0.75ra处环量较大时,可有效提升大流量工况处空化性能,如环量组合7、11、12、13和17。
因此,在保持叶轮设计工况处扬程基本不变的前提下,叶轮在各个工况下空化性能均对环量分布形式极为敏感,特别是大流量工况与设计流量工况。在混流泵的设计中,需根据实际需求谨慎选择叶轮出口处翼展方向环量的分布形式。
4.3 内流场
由于环量组合数目较多,若对比所有组合,则所需篇幅过大,为说明环量分布形式对内流场的影响,选取其中具有代表性的环量组合1、2、3、14和15进行内部流场对比分析。
5种环量组合对应的叶轮出口翼展方向轴面速度与总压分布如图8所示,由图可知由于轮毂和轮缘处受壁面影响,压力梯度与速度梯度变化较大,影响范围约为总翼展长度的10%。在叶片出口其它位置,对比环量组合1,可以看出环量分布对轴面速度的影响十分明显,当某处环量较小时,该处轴面速度随之减小,反之亦然,且越靠近轮毂侧,该影响越强烈。其对叶轮出口总压分布具有相似影响,环量值较大处,总压随之增大,如环量组合1对应的翼展方向近似于等压分布,而环量组合15所对应的翼展方向总压分布则明显表现出轮缘侧大于轮毂侧,环量组合14与之相反。
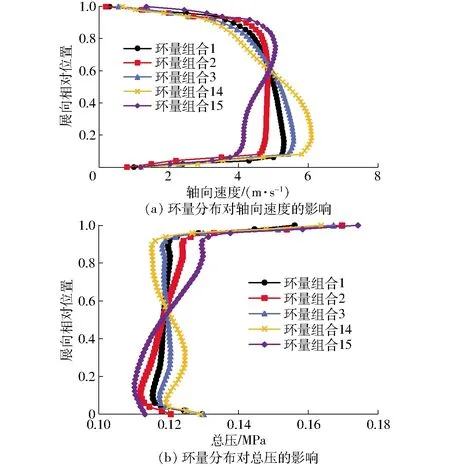
图8 环量分布对内流场的影响Fig.8 Influence of circulation distribution on inner flow field
因此,通过改变翼展方向环量分布形式,可以有效改变叶轮做功能力与内部流场,进而影响叶轮下游部件的性能,且相较于线性环量分布,非线性环量分布具有更大的改变空间。
5 结论
(1)在反问题设计中,叶轮出口翼展方向环量分布形式对混流泵叶轮性能存在较大影响,且对不同工况点、不同目标参数呈现不同作用,因此在混流泵的多工况、多目标设计优化中,叶轮出口翼展方向环量分布可起到重要作用。
(2)叶轮出口翼展方向环量分布对叶轮内部流动状态具有较大影响,在对应位置处,环量与轴向速度和总压成正比,通过改变环量分布形式可有效改变叶轮出口处的流动状态,进而影响叶轮下游部件性能。
(3)针对不同工况点和不同目标参数,相较于翼展方向环量线性分布,存在更优的非线性分布形式。为有效提升叶轮效率,应给予翼展中后部较大的环量和轮缘处较小的环量;为提升小流量点和设计点的空化性能,应给予0.75ra处较小环量和轮缘处较大环量;为提升大流量点空化性能,应给予轮毂、轮缘处较小环量以及翼展0.75ra处较大环量。

