环量控制扑翼式获能器气动特性的数值研究

倪思彤，史方锐，孙晓晶

（上海理工大学 能源与动力工程学院/上海市动力工程多相流动与传热重点实验室，上海 200093）

作为无污染的可再生能源，风能和水流能的开发和应用目前得到越来越广泛的重视［1-2］。扑翼作为一种可以从流体（风或水流）中提取能量的获能装置，因其能量转换效率不高长期以来没有得到广泛应用，探索提升其获能特性的有效途径已经成为新能源开发利用的热点之一。主动流动控制技术可根据实际需要灵活调节激励参数以控制流场，该技术通常比被动控制技术对效率的提升效果更好，因而受到研究人员的青睐。目前应用在扑翼上的主动控制技术主要集中在摆动式格尼襟翼及柔性变形两类。柔性扑翼通过主动控制翼型产生变形影响其前缘涡的发展演化，提高上、下翼面的相对压力差，从而可以产生更高的推力或升力［3-5］。而在扑翼尾缘安装主动式格尼襟翼则是利用襟翼的摆动改变翼型弯度，改善翼型的气动特性，增强其做功性能，使扑翼的获能效率最高可提升22%［6-8］。

环量控制（circulation control）是一种常见的主动流动控制技术。该技术通过在翼型圆弧后缘两侧表面设置切向射流，利用流体在曲面外表面流动时产生的柯恩达效应，推迟边界层流动分离，增加翼型环量，进而提高翼型的升力［9］。Frith等［10］尝试用环量控制器替代传统飞机的操纵舵面进行试验，探究应用环量控制技术操纵飞机的可行性。齐万涛等［11］发现双射流环量控制器在较低的动量系数下可实现飞机姿态控制功能，增加其纵向稳定性，并能够显著提高升力，并改善飞行器的短距起降性能。目前环量控制方法开始逐渐被应用于提升风力机翼型的气动特性。郑无计等［12］探究了环量控制技术对超临界翼型气动特性的影响，结果表明在合适的动量系数下，环量控制方法可使翼型在较小的迎角工况下产生更高的升力，从而具有更好的气动特性。乔晨亮等［13］针对实施环量控制后的钝尾缘翼型性能进行研究，发现翼型的气动特性明显改善，且具有比传统翼型更高的升阻比。雷玉昌等［14］对环量控制翼型的气动力迟滞效应进行了数值模拟，研究了其在非定常运动状态下的性能，发现在小迎角下提高环量动量系数有助于减小气动力迟滞效应，而在大迎角下使用高动量系数环量控制则可能导致翼型表面动态失速提前。此外，雷玉昌等［15］还探究了采用脉冲射流影响环量控制翼型气动性能的规律，结果表明，与定常射流相比，采用脉冲射流提高环量控制翼型在大迎角下的气动特性的效果更为显著，且所需射流的质量流量更小。杜海等［16］设计了一种多级环量控制翼型，并采用粒子图像测速（PIV）技术对其增升效果进行了实验测试，发现采用多级环量比单级环量控制技术在增升效果和降低能耗方面更有优势。Shires等［17］对具有不同尾缘的环量控制叶片的垂直轴风力机气动性能进行了对比分析，结果表明：在低动量系数下，椭圆弧尾缘翼型的升阻比系数更大。Wilhelm等［18］采用数值方法探究了动态环量控制对垂直轴风力机性能的影响，发现动态环量控制系统可在提升垂直轴风力机风能利用率的同时降低射流动量需求。Gorle等［19］对采用环量控制技术的升力型直叶片垂直轴风力机和水轮机的获能效率进行了分析，发现与连续环量控制相比局部可变环量控制提升风力机功率输出的效果更为明显。而将环量控制方法用于提高扑翼型装置获能效率的研究尚未见报道。

本文提出一种新型环量控制扑翼型获能器，采用数值模拟方法对这种扑翼的气动性能进行了分析，并将其获能效率与传统扑翼及表面施加协同射流控制扑翼进行对比，以验证新型扑翼的获能特性。此外，还在四种射流速度变化模型即连续式、方波式、正弦式和三角波式下对新型扑翼获能性能进行数值模拟，探究不同射流喷射模式在能耗需求和提升扑翼气动性能方面的不同。

1 数值方法

为方便研究，扑翼运动模式可简化为升沉运动和绕某点的俯仰运动的合运动。扑翼运动简化模型示意图如图1所示，其中：c为扑翼弦长；U∞为来流速度；H(t)为翼片在垂直方向上的位移；t为时间；H0为升沉幅值，表示翼片在垂直方向上最大位移的绝对值；θ(t)为俯仰角度，表示来流方向与翼型弦线方向的夹角；θ0为俯仰幅值，表示最大俯仰角度；d为扑翼扫掠面积，在二维中即为扑翼尾缘扫掠高度。

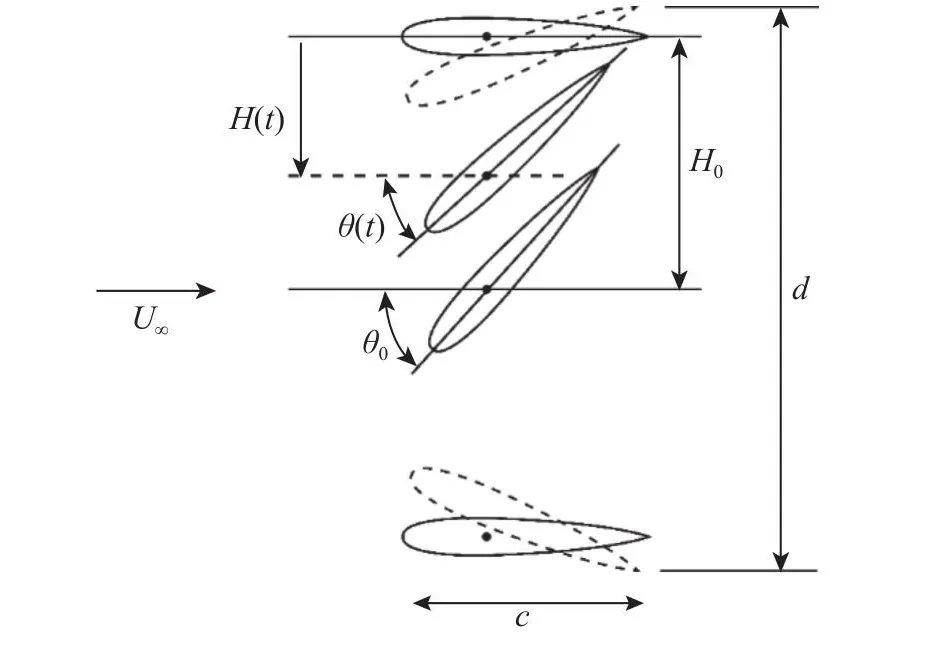
图1 扑翼运动简化模型示意图Fig.1 Heaving and pitching motion of a flapping wing

升沉运动和俯仰运动的运动方程定义为

式中：f为翼型扑动频率；φ为升沉运动与俯仰运动之间的相位角，取φ=90°。

对式（1）、式（2）求导得到扑翼的升沉速度与俯仰角速度分别为

式中：Vy(t)为扑翼瞬时升沉速度；ω(t)为扑翼瞬时俯仰角速度。

扑翼运动时可将流体作用于扑翼的力分解为升沉力Fy和俯仰力矩M，升沉力做功Py(t)和俯仰力矩做功Pθ(t)之和为获能总功率P，即

式中：和分别为时均升沉功率系数和时均俯仰功率系数；CY为 升沉力系数，CY(t)=为密度；CM为俯仰力矩系数，为翼型扑动周期。

环量控制射流功率Pj为

式中：vj为 射流出口流速；Aj为射流口面积。

射流介质和来流介质相同，所以来流介质密度ρ∞和射流介质密度ρj相同。因此射流能量系数Cj为

一个周期内平均射流耗能系数为

环量控制扑翼的净获能效率ηnet计算式为

2 网格及模型验证

本文研究所用的环量控制翼型是在NACA0012的基础上修改而来，在距离前缘75%弦长处(l=75%c)的翼型尾缘两侧分别开设高度h为0.2%c的射流口，并生成半圆弧形柯恩达尾缘。环量控制扑翼翼型示意图如图2所示。采用Pointwise网格划分软件绘制扑翼网格，并利用Fluent软件中用户自定义函数(UDF) 计算动网格，将内部非结构网格域设置为变形域（deforming），通过给定的运动方程与控制参数实现计算过程中的网格重构。计算域及边界条件和扑翼表面局部网格放大图如图3所示，其中：I为内部计算域；II为外部计算域。内部计算域I为动网格域，半径为3c，采用非结构网格组成，对翼型前缘及射流口附近网格进行加密，并且第一层网格高度为1×10-4，满足描述壁面网格厚度的无量纲数Y+≈1；外部计算域II为结构网格域，半径为30c，计算域I与II通过交界面（interface）连接。翼型表面设置为无滑移壁面，进、出口边界条件分别为速度入口与压力出口。

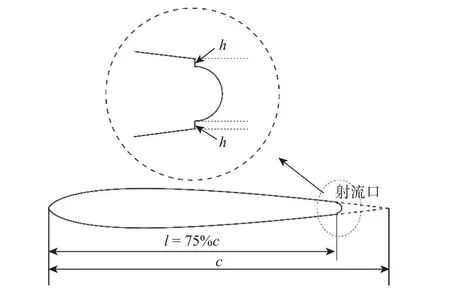
图2 环量控制扑翼翼型示意图Fig.2 Schematic diagram of a circulation controlled flapping wing

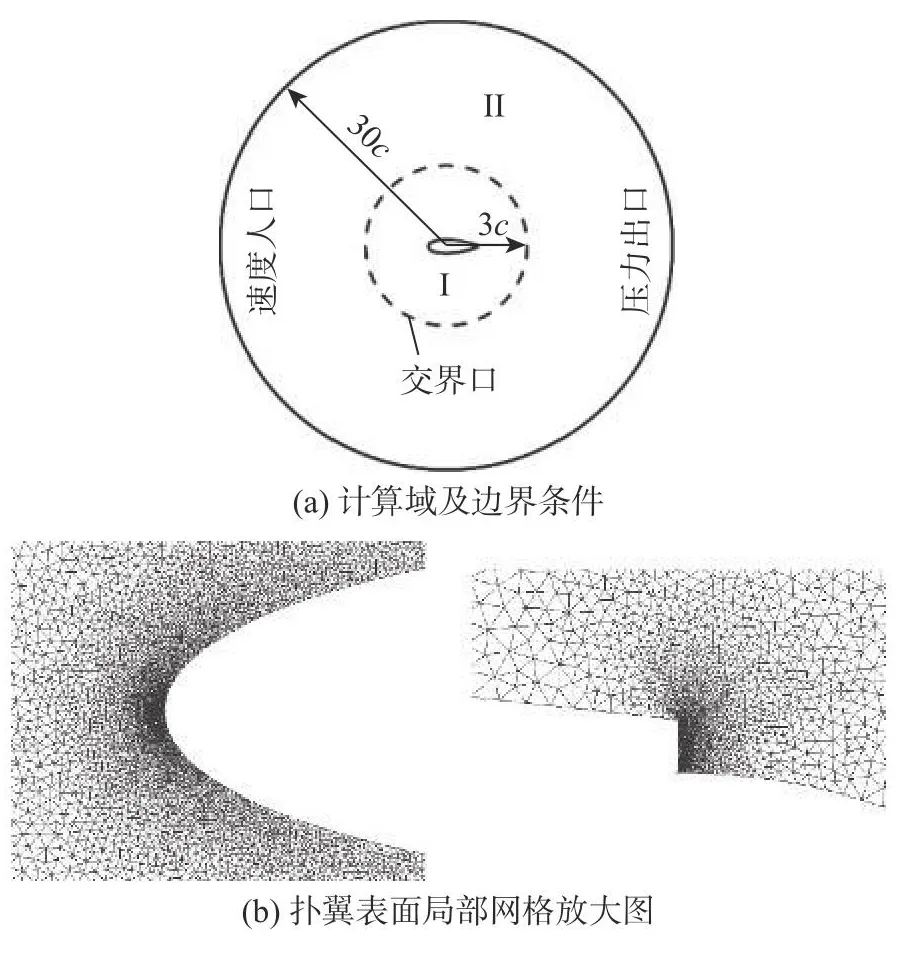
图3 计算域及边界条件和扑翼表面局部网格放大图Fig.3 Computational domain,boundary conditions and enlarged view of the mesh

为保证数值模拟的时间精度与空间精度，在三组工况参数下分别对时间步长与网格数量的变化对计算结果的无关性进行验证。经过一系列计算，并综合考虑计算精度及资源消耗，选择中网格（网格数量约为120 000）和时间步长T/2 000作为后续计算的基准参数。

为了验证数值模拟的可信度，将模拟结果与文献中的实验值[20]和模拟值[21]进行了对比，结果如图4所示。根据文献[20]中的实验数据，选取NACA0012翼型为模拟对象，雷诺数Re=13 800，折合频率f*=0.16，升沉幅值H0=1.23c，俯仰幅值θ0=85.9°。以空气为工质，选择Spalart-Allmaras湍流模型进行数值模拟计算。本文采用的二维模拟方法忽略了受翼型三维展向长度的影响导致计算得到的升力系数偏大于实验值，但两者整体变化趋势具有较好的一致性，且与文献[21]中的模拟值吻合良好，从而验证了本文数值方法的可靠性。

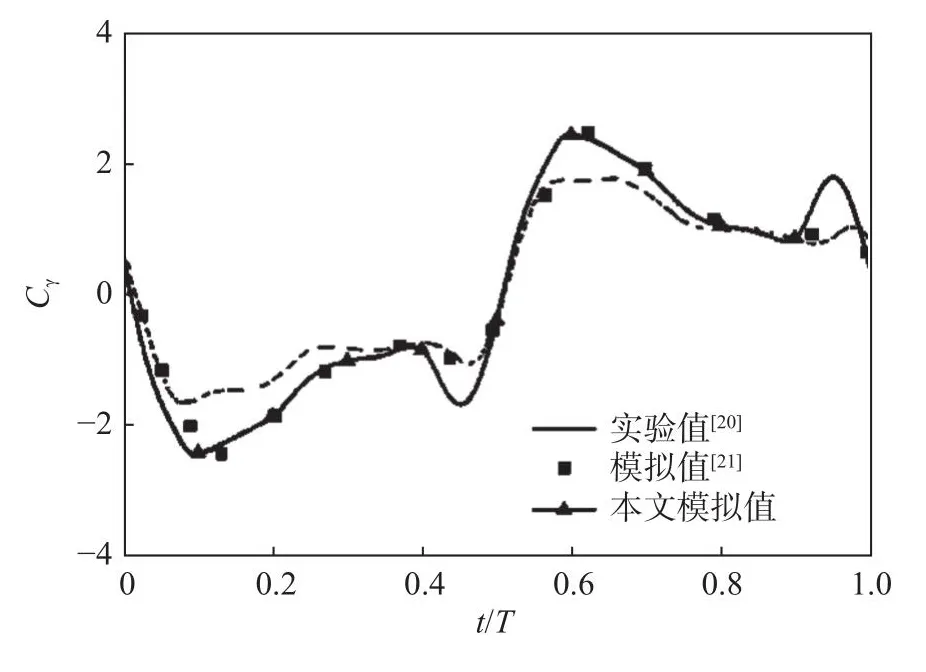
图4 本文模拟得到的升沉力系数与文献中实验值和模拟值的对比Fig.4 Comparison of the coefficient of heaving force between the obtained results and the results in the literatures

3 结果与讨论

3.1 环量控制扑翼与协同射流控制扑翼获能效率的对比

对翼型尾缘采用环量控制的扑翼的气动性能进行数值模拟，升沉幅值H0/c= 1.23，俯仰幅值θ0=70°，并将结果与采用协同射流控制的扑翼获能效果进行对比。协同射流控制扑翼翼型示意图如图5所示，据文献[22]中的研究结果，将前缘喷气口设置在翼型吸力面距离前缘 3%c处，高度为0.6%c，尾缘吸气口设置在翼型吸力面距离前缘85%c处，高度为1.2%c。

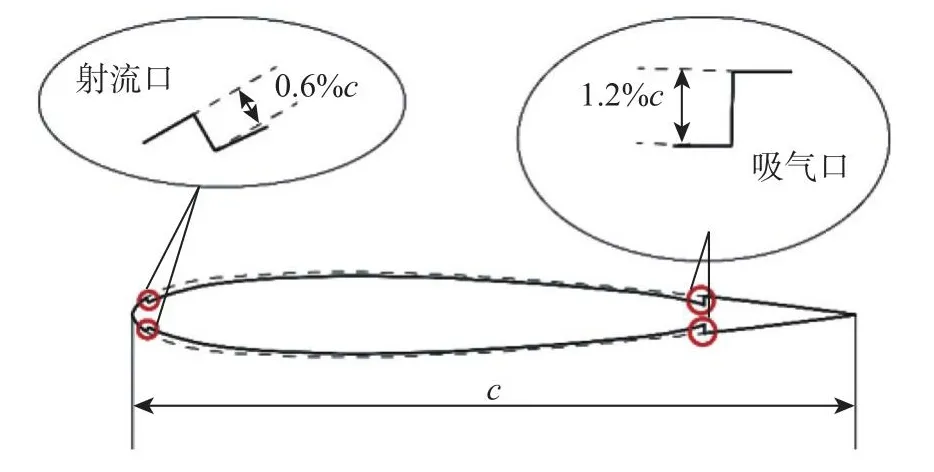
图5 协同射流控制扑翼翼型示意图Fig.5 Schematic diagram of a co-flow jet control flapping wing

图6为动量系数Cμ= 0.20时传统扑翼、环量控制扑翼（CC）和协同射流控制扑翼（CFJ）获能效率的对比。可以看到，与传统扑翼相比，采用环量控制方法在所有折合频率下对获能效率均有明显的提升效果，且当射流的动量系数即能耗相同时，环量控制扑翼获能效率的提升幅度显著高于协同射流控制扑翼，表明该方法在降低能耗、提升获能效率方面具有一定的优势。

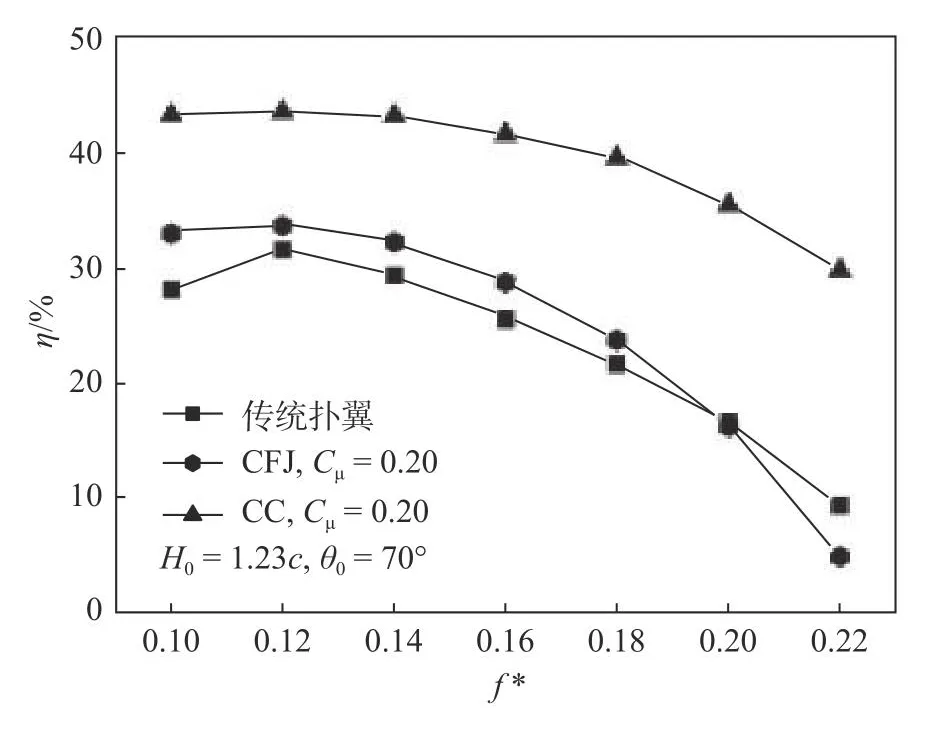
图6 相同动量系数下传统扑翼、环量控制扑翼和协同射流控制扑翼获能效率的对比Fig.6 Comparison of energy harvesting efficiency between the baseline，circulation control flapping wing and co-flow jet flapping wing

图7为当f *= 0.12、Cμ=0.20时，传统扑翼与施加主动控制扑翼的升沉力系数CY、俯仰力矩系数CM、升沉力做功系数CPY和俯仰力矩做功系数CPθ在一个周期内的变化。在整个运动周期内，传统扑翼和环量控制扑翼的升沉力系数曲线均在t=0.45T时出现第二个峰值，且与升沉速度的同步性较好；而协同射流控制扑翼的升沉力系数曲线仅存在一个峰值，在t=0.30T～ 0.50T时升沉力骤降，因此在一个周期内，升沉力在部分时刻做负功。协同射流控制扑翼的俯仰力矩在一个周期内始终与其速度的同步性较差，导致俯仰力矩始终做负功。虽然传统扑翼和环量控制扑翼的俯仰力矩与其速度在近半个周期内同步性较好，而施加环量控制增大了俯仰力矩幅值，因此环量控制扑翼俯仰力矩所做正功与负功皆高于传统扑翼。总体而言，尾缘采用环量控制大大提高了扑翼上受到的升沉力，使翼型做功能力显著增强。

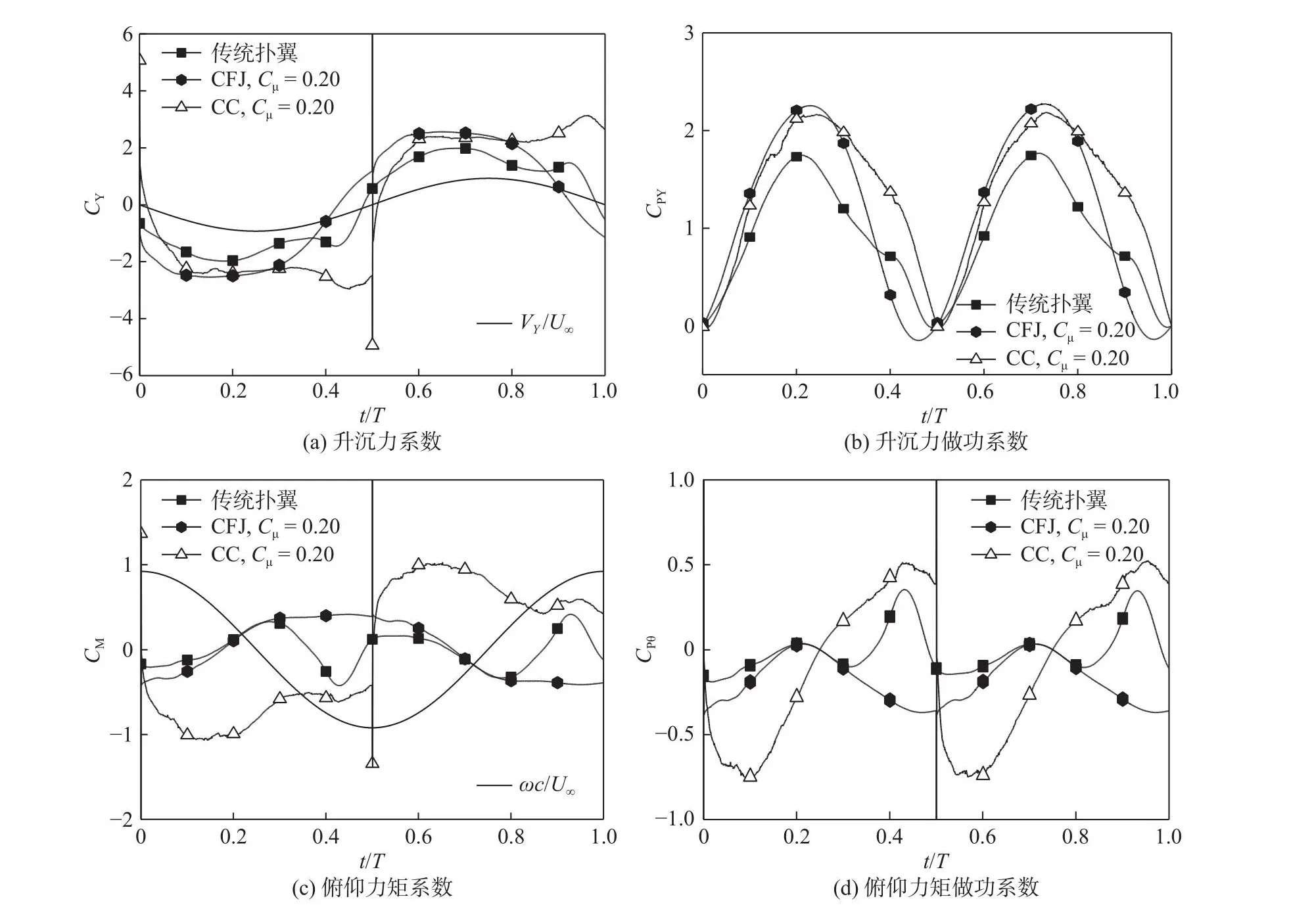
图7 传统扑翼与施加主动控制扑翼的CY、CPY、CM 和CPθ 在一个周期内的变化Fig.7 Variations of CY, CPY，CM and CPθ curves of the baseline and active flow controlled flapping wing in one period

图8、图9为传统扑翼、环量控制扑翼和协同射流控制扑翼在不同时刻绕流流场瞬时压力云图和涡量云图。在t=0.25T时，与传统扑翼相比，环量控制扑翼与协同射流控制扑翼两侧压差均大幅增加，且升沉速度达到峰值，与升沉力同步性较好，因此升沉力做功最为显著。在t=0.45T时，俯仰力矩做功占功率输出的主要部分，传统扑翼和环量控制扑翼吸力面均存在负压区，但环量控制扑翼的负压区范围更广，且强度高于传统扑翼，因而此时环量控制扑翼升沉力幅值最高。环量控制吸力面负压区的存在同时阻碍了翼型前缘的上仰运动趋势，因此产生了阻碍翼型运动的俯仰力矩，使俯仰力矩做负功。协同射流的喷气口位于翼型前缘，吸气口位于翼型尾缘，协同射流的存在完全抑制了一个周期内前缘涡的产生与发展，导致扑翼在运动周期内不能合理利用前缘涡与升沉-俯仰耦合运动相匹配所获得较高的获能效率。此外，协同射流控制扑翼吸力面尾缘为正压区，会产生阻碍尾缘下俯运动的俯仰力矩，使俯仰力矩对扑翼整体获能的贡献变成负值。

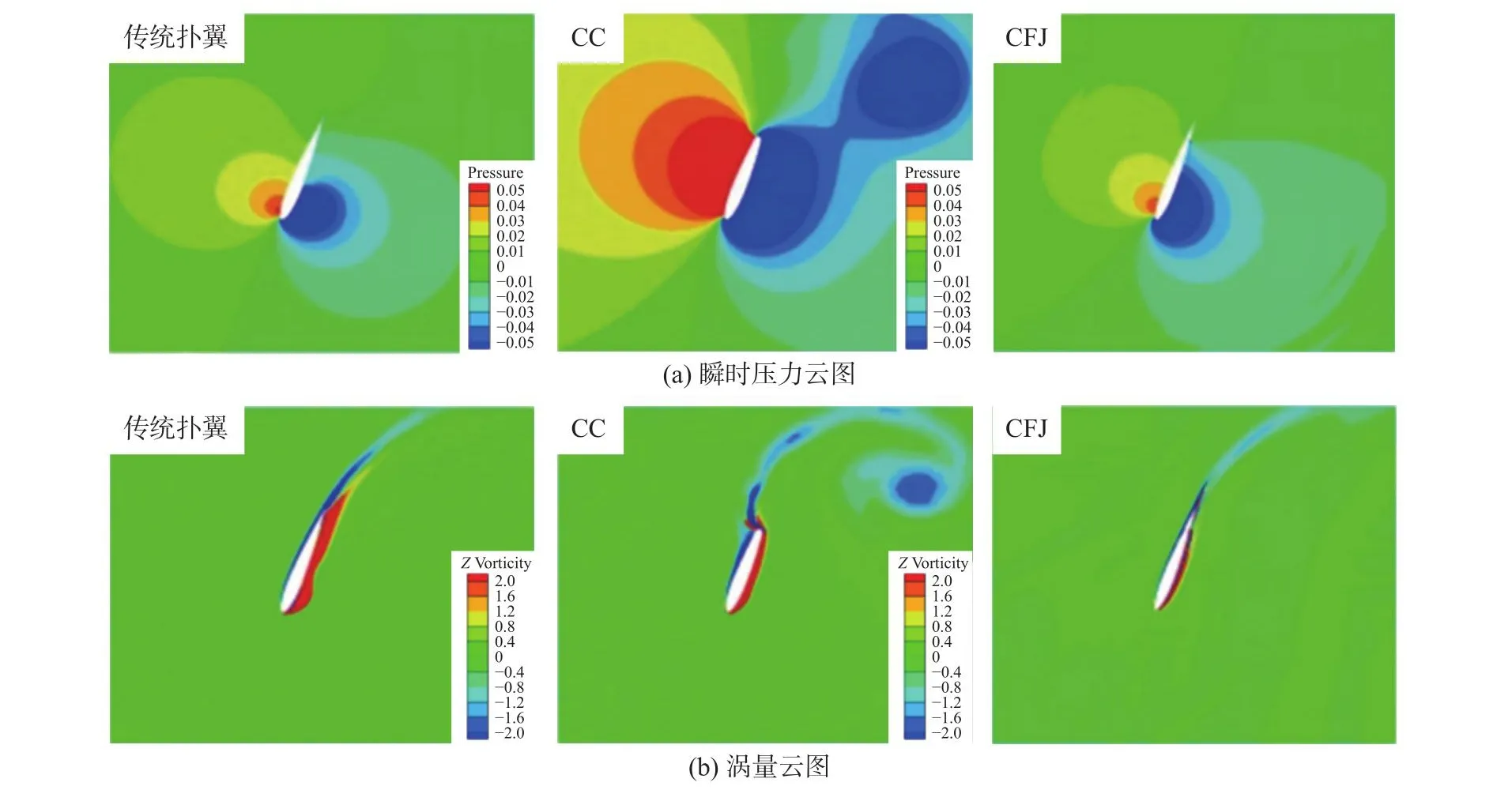
图8 t=0.25T时传统扑翼、环量控制扑翼和协同射流控制扑翼绕流流场对比Fig.8 Comparison of the flow field around a flapping wing among the baseline, circulation controlling and co-flow jet controlling at t=0.25T

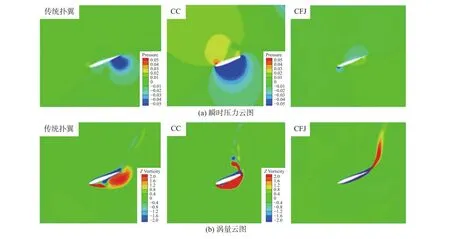
图9 t=0.45T时传统扑翼、环量控制扑翼和协同射流控制扑翼绕流流场对比Fig.9 Comparison of the flow field around a flapping wing among the baseline , circulation controlling and co-flow jet controlling at t=0.45T

3.2 射流喷射模式对环量控制扑翼性能的影响

为了进一步降低环量控制中施加射流所需的能耗，对不同环量控制方法对扑翼性能的影响进行了研究。图10为不同射流模式下射流速度变化。对四种射流模式（连续式、方波式、正弦式和三角波式）下该新型扑翼获能性能进行数值模拟，探究不同射流模式在能耗需求和提升扑翼气动性能效果方面的不同。

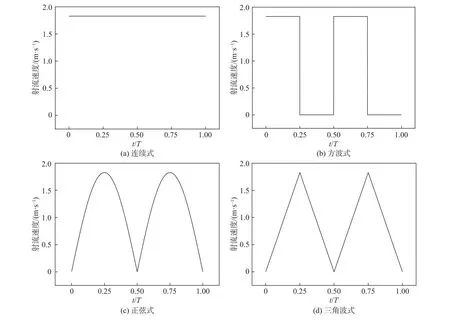
图10 不同喷射模式的射流速度变化Fig.10 Evolution of the jet velocity under different jet patterns

图11(a) 为不同射流模式下的环量控制扑翼在不同折合频率下的获能效率对比。方波式环量控制扑翼的获能效率整体最高，连续式环量控制扑翼的次之，正弦式和三角波式的相近，其中在低频及高频工况下，三角波式环量控制扑翼的获能效率均低于正弦式。与传统扑翼相比，环量控制扑翼的获能效率最高可达到47.51%（方波式环量控制扑翼，f*=0.12,l=75%c,θ0=70°,Cμ=0.20），但环量控制作为主动控制方法，能耗问题不可忽视，各射流控制模式的能耗可根据式(10)～(12)计算得出。

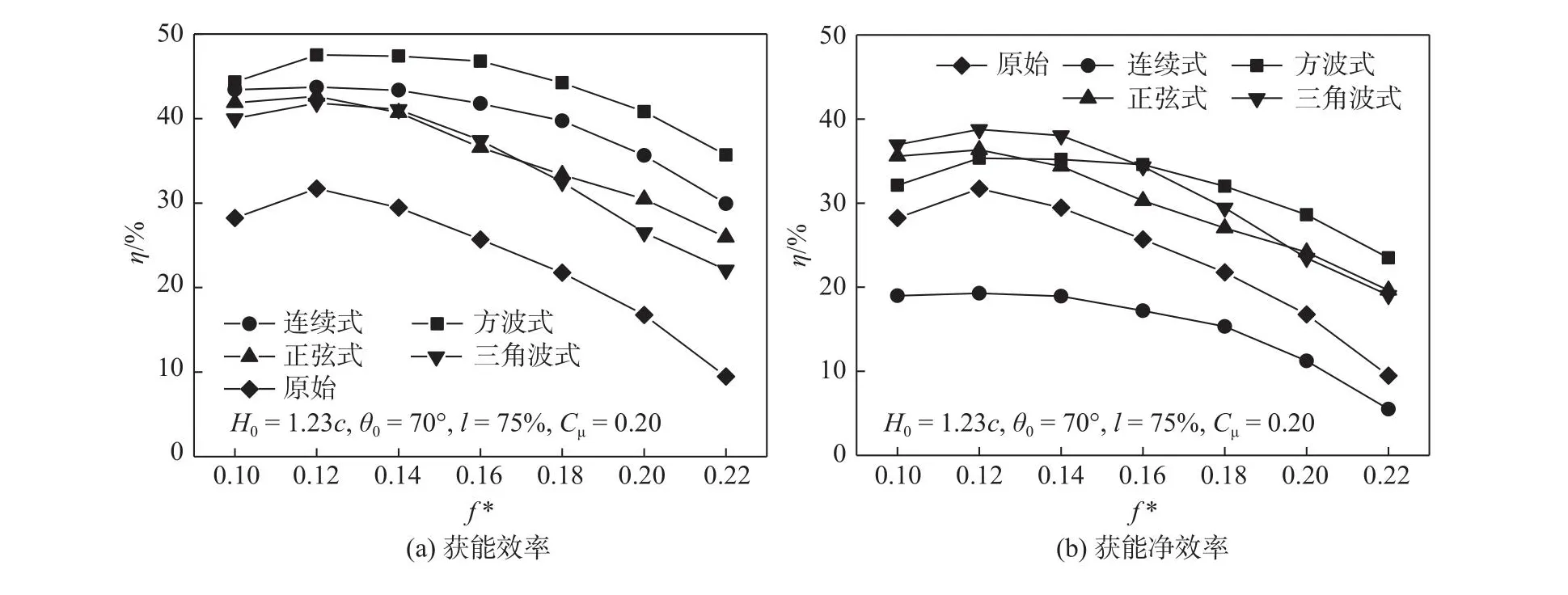
图11 不同射流模式下环量控制扑翼的获能效率与获能净效率对比Fig.11 Comparison of the energy harvesting efficiency and net energy harvesting efficiency of a circulation controlled flapping wing with different jet patterns

图11(b) 为不同射流模式下环量控制扑翼在不同折合频率下考虑射流能耗后得到的净获能效率。从图中可知，由于连续式环量控制扑翼的射流速度在整个周期内均保持峰值，方波式环量控制扑翼能耗为连续式的一半，而正弦式与三角波式环量控制扑翼的射流速度仅在某些时刻保持较高水平，因此连续式扑翼的能耗最高，方波式、正弦式和三角波式的能耗依次降低，其中三角波式环量控制扑翼的获能净效率最高，在f*=0.12工况下可达38.77%。

选择f*= 0.12典型工况下的流场对不同射流模式影响扑翼获能效率的规律进行深入分析。扑翼的升沉力系数CY、 俯仰力矩系数CM、升沉力做功系数CPY和 俯仰力矩做功系数CPθ在f*=0.12时的变化如图12示。从升沉力系数来看，低频时升沉力方向与运动方向始终保持一致，升沉力做正功。连续式和方波式扑翼在运动前期升沉力较大，当正弦式和三角波式扑翼的射流速度逐渐增大至峰值后，除方波式扑翼外其余三种扑翼的升沉力大小几乎一致。在0.25T～0.50T及0.75T～ 1T时方波式扑翼射流速度为0，三角波式和正弦式扑翼的射流速度从峰值逐渐减小至0，因此这三种扑翼产生的升沉力相近且均小于连续式扑翼。从俯仰力矩的角度来看，其方向在大部分时间内都与俯仰角速度方向相反，导致俯仰力矩在一个周期内负功输出较多。表1为一个周期内不同射流模式下环量控制扑翼的平均升沉力做功系数、平均俯仰力矩做功系数、平均功率系数和获能效率的对比。总体来说，虽然方波式和连续式扑翼的俯仰力矩输出负功较多，但幅值均较小，且方波式扑翼上受到的升沉力输出正功远高于其他三种扑翼，因此采用方波式射流的环量控制扑翼的获能效率最高。

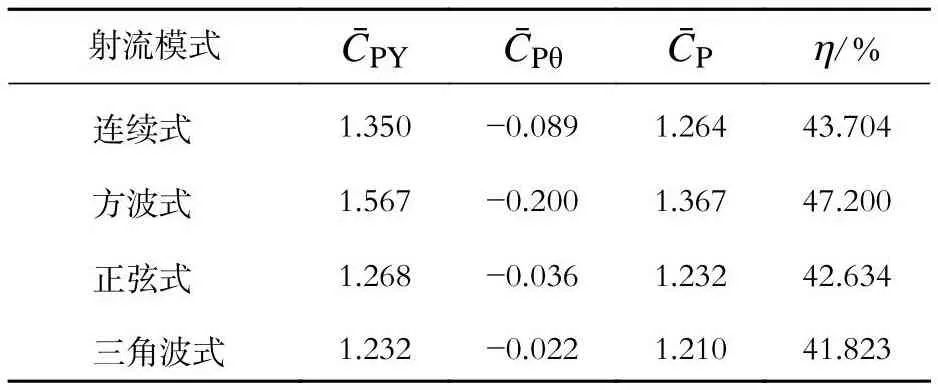
表1 不同射流模式下环量控制扑翼的获能效率对比（f＊ =0.12）Tab.1 Comparison of the energy harvesting efficiency of a circulation controlled flapping wing with different jet patterns at f＊ = 0.12

图12 不同射流模式下环量控制扑翼的CY、CPY 、CM和CPθ在一个周期内的变化Fig.12 Variations of CY, CPY, CM and CPθ of a circulation controlled flapping wing with different jet patterns in one period

图13为当f*=0.12时，采用不同射流控制模式下环量控制扑翼分别在t=0.25T和0.55T时绕流流场瞬时压力云图及涡量云图。当扑翼运动至t=0.25T时，与其他三种射流方式相比，采用方波式射流模式的扑翼前缘明显产生了沿翼型吸力面运动的前缘涡，其诱导产生的负压区会增大吸力面负压区的范围，增大翼型环量，促使扑翼产生较大的升沉力。从瞬时压力云图可看出，采用方波式射流模式的扑翼两侧存在较大的压差，而此时扑翼升沉速度达到最值，故升沉力做功最为显著。当t=0.55T时翼型处于顺时针运动状态时，升沉速度较低，而俯仰角速度位于峰值附近，故升沉力做功较少，功率输出主要由俯仰力矩贡献，但俯仰力矩方向与俯仰角速度方向相反，因此此时俯仰力矩做负功。扑翼从水平位置开始运动，翼型吸力面与压力面相互交替。受射流产生的负压区影响，此时连续式射流扑翼翼型的下翼面正压与负压相抵消，表现为仅在压力面尾部存在小范围的正压区。而方波式射流扑翼因在0.25T～ 0.50T和0.75T～T时无射流，吸力面不存在大范围的负压区，因此在交替后的压力面存在较大范围的正压区，因此在t=0.55T时连续式射流扑翼产生的升沉力小于方波式射流扑翼。而正是由于压力面尾缘正压区的存在，其与上翼面的负压区相结合产生了使扑翼逆时针旋转的俯仰力矩，从而削弱了方波式射流扑翼俯仰力矩做正功的效果。正弦式和三角波式射流扑翼吸力面射流速度较低，因而产生的负压区范围较小，翼型两侧相对压差较小，同时俯仰力矩输出负功较少。

图13 t=0.25T、t=0.55T时不同射流控制模式下环量控制扑翼绕流流场的瞬时压力云图和涡量云图 (f＊ =0.12)Fig.13 Comparison of the instantaneous pressure contour and vorticity contour of a circulation controlled flapping wing with different jet patterns at t=0.25T, 0.55T and f＊ =0.12

4 结 论

本文提出了一种在翼型尾缘处施加环量控制以提高扑翼获能器气动性能的新方法，采用数值模拟对该方法的实际效果进行了评估。此外，为了降低射流能耗，设计了四种射流喷射策略，并对不同环量控制下扑翼获能效率和能耗进行了对比分析，主要结论为：

(1) 在扑翼上施加不同射流模式的环量控制后扑翼获能效率与传统扑翼相比均得到不同程度的提升。从获能效率方面看，施加方波式射流的环量控制扑翼的获能效率最高，可达47.51%，比传统扑翼的获能效率高49.8%，连续式射流扑翼次之，正弦式和三角波式扑翼获能效率较低。

(2) 对不同射流模式下环量主动控制所需能耗进行了分析，结果表明：连续式环量控制扑翼能耗最多，方波式能耗为连续式的一半，正弦式和三角波式射流能耗依次减小。因此，由于三角波式环量控制扑翼的能耗最低，在原获能效率的基础上扣除主动环量控制所需能耗后得到的获能净效率最高可达38.77%，比传统扑翼相比提升幅度达22.2%。

本文研究结果表明，环量控制方法具有调控灵活、低能耗、实用性强且提升获能效果明显的优点，具有实际应用潜力。然而本文工作都是基于二维非定常数值模拟，未考虑实际叶片表面的三维流动对其气动性能的影响，在后续研究中拟采用高精度的数值模拟方法如分离涡模拟（DES）进行三维数值模拟，对叶片表面流动细节进行深入分析，探讨采用环量流动控制方法提高扑翼获能效率的流动机理，为这种新型扑翼样机的研制与开发提供理论指导。此外，在后续工作中还将进行小型实验模型的设计与加工，开展相关性能试验，以验证数值结果的可靠性。