封闭腔体排液孔的流量系数研究*

胡仁强，张 涛，卢柳韵，许常悦

（南京航空航天大学 飞行器环境控制与生命保障工业和信息化部重点实验室，南京 210016）

引言

封闭腔体排液流动有诸多的应用场景，如航空发动机短舱排液、管路排液以及飞机燃油箱串油等.封闭腔体排液孔的流动本质上属于小孔流动.通过调研发现，近年来有关小孔流量系数的研究较为广泛.目前，人们关于小孔流量系数的研究主要聚焦于如下两个方面：一是小孔流量系数的影响因素研究；二是小孔流量系数的经验公式研究.

小孔流动的流量系数受到诸多因素影响，如小孔几何参数、小孔形状、小孔加工工艺（孔口倒角）等.聂俊领[1]研究了小孔几何参数对流量系数的影响，当小孔的长度与直径的比值趋于一个较大值时，小孔的流量系数趋于一个定值.吴进军等[2]对鳞片状孔的流量系数进行了研究，结果表明孔的直径越大，鳞片状孔的流量系数也越大.Ding 等[3]研究了飞机起落架减震器中的小孔几何参数（小孔长度与直径比l/d、小孔直径与管道直径比d/D）及Reynolds 数对小孔流量系数的影响.他们指出Reynolds 数对小孔流量系数的影响较为复杂，l/d的值越大，小孔的流量系数越小.曹睿等[4]对垂直锐边小孔的流量系数进行了研究，他们发现，小孔直径和小孔厚度对流量系数存在耦合影响.郭成富等[5]利用实验手段研究了倒角圆孔的流量系数，分析了不同倒角的小孔流量系数.研究发现，倒斜角和倒圆角的小孔流量系数均大于垂直锐边孔的流量系数.史维祥和葛思华[6]也对小孔流量系数开展了实验研究，结果表明在不同油压差下，小孔直径增加，流量系数显著上升.此外，基于对实验数据的分析，他们还提出了计算小孔流量系数的经验公式.Webster 等[7]研究了流体的可压缩性对带倒角和不带倒角的小直径比锐边孔板流量系数的影响，结果表明，压缩性对倒角和未倒角孔的流量系数影响均很大；与不可压流体相反，倒角孔的流量系数比未倒角孔的流量系数小.

人们在研究小孔流量系数的厚径比尺寸影响时还发现，小孔存在薄孔和厚孔两种类型[8].当厚径比小于1.5 时，小孔流量系数变化非常剧烈；当厚径比在2 ～ 10 范围之内，且Reynolds 数大于2 × 104时，小孔的流量系数会保持一个恒定值[9].虽然人们发现了薄孔和厚孔的流量系数不同，但是对其流动机理的差异分析较少.

为了便于工程应用，需要建立小孔流动的流量系数计算公式.例如，Abd 等[10]利用实验手段研究了孔径和Reynolds 数对小孔流量系数的影响，得到了大量的实验数据，并建立了计算小孔流量系数的经验公式.Fu 等[11]试验研究了堰孔的流量系数，通过量纲分析推导了流量系数与四个无量纲参数的关系式，并对流量系数经验公式进行了优化和验证.Eghbalzadeh 等[12]通过试验获取了渠道侧壁孔的流量系数，提出了考虑孔形状影响的侧壁孔流量系数计算公式.Werth 等[13]提出了用小孔的投影面积和表面积来确定小孔流量系数的方法，并给出了这两种方法的计算公式.除此之外，黄一帆等[14]根据数值模拟结果得到了一种新的经验公式，该经验公式可以预测T 型微通道内幂律流体液滴破裂的不同流型.虽然人们已经得到了一些经验公式，但是这些公式普适性较差.

流量系数是表征小孔流动性能的重要参数，但小孔的流量系数受诸多因素的影响.虽然近年来可以见到不少有关对小孔流量系数的研究报道，但是仍缺乏对小孔流量系数影响因素的系统研究.此外，工程上希望能够有一类应用广泛、可靠度高的小孔流量系数计算公式.本文采用两相流数值方法对排液孔流动进行模拟，以此得出大量工况下的小孔流量系数.基于对大量数据的分析，借助量纲分析方法获取适用于不同工况的小孔流量系数预测公式，旨在为工程上小孔的流量系数计算提供理论参考.

1 物理模型和数值计算方法

1.1 物理模型

在当前计算中，需要对封闭腔体进行建模，并在其底部中心开圆形小孔.建立的计算模型为圆弧状旋成体.为了模拟液体从封闭腔体内部的排出过程，在小孔下方设置一个圆柱形计算域，图1 给出了计算模型的示意图以及排液孔局部的网格拓扑结构，第一层网格高度为5 × 10−5m，总网格数约为40 万.

需要说明的是，本文采用控制变量法来开展相关研究工作，分析水头高度h、水力直径d、厚度l等对小孔流量系数的影响.表1 给出了圆形小孔的几何参数.

表1 圆形排液孔的几何参数Table 1 Geometric parameters of circular drain orifices

1.2 数值计算方法

封闭腔体的排液过程属于不可压缩的气液两相流动.该流动过程不考虑传热影响，故流动的控制方程仅包含连续性方程和动量方程.在直角坐标系下，封闭腔体排液孔的流动控制方程可以写成如下形式：

在控制方程(1)和(2)中，ui表示速度分量，p为流体静压，F为体积力，ρ和 τij分别为混合介质密度和黏性应力项：

其中，α为气相体积分数，ρl为液相密度，ρg为气相密度，Sij=0.5(∂ui/∂xj+∂uj/∂xi)为应变率张量，µ为流体黏性系数.气液两相的界面捕捉可采用基于level-set 的volume of fluid（VOF）方法，王金城等[15]曾采用VOF 方法研究水滴撞击壁面形成气泡群的问题，尹强等[16]也曾采用VOF 方法研究了液滴的对心碰撞过程.由于本文研究的封闭腔体排液孔流动的Reynolds 数最大约为O(104)，故需要考虑湍流影响.这里采用Reynolds 平均Navier-Stokes（RANS）方法进行湍流计算，黏性应力项的计算公式需进行如下改写：

其中，µL为分子黏性系数，µT为湍流黏性系数.µT需要通过湍流模型进行求解，本文采用的湍流模型是文献[17]提出的realizablek-ε 两方程模型.

控制方程(1)和(2)的求解采用基于交错网格的Simple 算法，动量方程和湍流模型方程的离散采用二阶迎风格式，本文的数值模拟工具采用的是商用软件FLUENT.图1所示的计算域入口和出口边界处设为定压条件，即一个大气压，固壁为无滑移无穿透的黏性壁面.

图1 封闭腔体简化模型及排液孔局部的网格拓扑结构Fig.1 The simplified model for the closed cavity and the mesh topology of the drain orifice

1.3 排液孔流量系数的量纲分析

量纲分析方法常用于构建物理量之间的相关关系.为了获取封闭腔体排液孔流量系数的计算公式，首先需要获取影响流量系数的物理量.在工程上，小孔的流量系数有如下定义[18]：

其中，Q=vA为流经小孔的体积流量，A为小孔的横截面积，g为重力加速度，h为水头高度.我们知道，影响排液孔出流速度的因素有水头高度h、排液孔水力直径d、小孔厚度l、流体密度ρ、动力黏度µ以及重力加速度g.因此，可以构建如下隐函数：

根据π定理，选取d，v和ρ 为3 个基本量，可以用这3 个基本量组成如下4 个无量纲量：

其中，ai，bi和ci(i=1,2,3,4)为待定系数.根据量纲一致性原则可以得出这些待定系数的值，从而可以得出4 个无量纲量的具体形式如下：

依据π定理并结合式(7)和(9)，不难得出利用函数φ表达出的小孔出流速度v的计算式：

根据式(6)，小孔的流量系数计算公式可以写成如下形式：

2 结果与讨论

2.1 算例验证与计算细节

为了验证当前数值计算方法的可靠性，本文对锥形漏斗底部无厚度圆孔的排液流动进行计算，并与已有试验数据[19]进行对比.依据不同的小孔直径d和水头高度h，文献[19]给出了66 组试验数据.这里，随机选取四组工况下的小孔流量系数进行对比，如表2所示，表中exp 表示文献中的实验数据，num 表示数值计算的数据.可以看出，当前计算结果与试验数据吻合较好，这说明当前数值计算方法具有较好的可靠性.

表2 数值与试验结果对比Table 2 Comparison of numerical and experimental results

为了开展网格无关性验证，选取三种不同分辨率的网格对圆孔排液流动进行数值计算，即20 万(grid 1)、40 万(grid 2)和100 万(grid 3).用于验证的圆孔排液流动工况为：水头高度h= 50 mm、水力直径d= 10 mm、小孔厚度l= 2 mm.图2 给出了沿小孔中轴线上的流向速度分布，可以看出，网格数量40 万的计算结果与网格数量100 万的计算结果几乎完全吻合.因此，为了节省计算量，本文采用40 万的网格完成其余全部算例的数值计算.

图2 网格无关性验证结果Fig.2 Grid independence verification results

2.2 单一几何参数对排液孔流量系数的影响

由上述分析可知，影响小孔流量系数的几何参数有水头高度h、小孔水力直径d以及小孔厚度l.为了分析单一几何参数对小孔流量系数的影响，这里采用控制变量法研究流量系数随某一几何参数的变化规律.所谓控制变量法是在研究小孔流量系数随某一个影响因素的变化规律时，其他影响因素要保持一致.

图3 给出了小孔流量系数随孔厚度的变化，由图可知小孔流动存在薄孔和厚孔两种流动特性.这里选取的小孔水头高度为200 mm，小孔直径d取为5 mm.当小孔厚度呈现为薄孔特性时，流量系数约为0.61；当小孔厚度为厚孔特性时，流量系数约为0.8.

图3 小孔流量系数随孔厚度的变化Fig.3 Evolution of the discharge coefficient with the orifice thickness

图4 给出了小孔流量系数随小孔上方水头高度h的变化.这里选取的水头高度范围为10 ～ 500 mm，小孔直径d取为5 mm.考虑到薄孔和厚孔特性的影响，小孔厚度l取为2 mm 和20 mm 两种规格.当h<200 mm时，小孔流量系数随水头高度的增加而减小，此时的液位称为低液位；当h≥200 mm时，小孔流量系数几乎保持一个定值，约为0.61，此时的液位称为高液位.由此可以看出，低液位时的小孔排液较快，而高液位时的小孔流量系数直接影响小孔排液的速率.

图4 小孔流量系数随水头高度的变化Fig.4 Evolution of the discharge coefficient with the head height

不同的工程问题对排液孔尺寸有不同的要求[20]，故需要研究小孔水力直径对流量系数的影响.图5 给出了圆形小孔流量系数随水力直径d的变化.这里，选取的小孔水力直径为5 ～ 20 mm，水头高度h为200 mm，厚度l取2 mm 和20 mm 两种规格.当l=2 mm时，水力直径对小孔流量系数几乎不存在影响.当l=20 mm时，水力直径较小的小孔Cd值较大，而水力直径较大的小孔Cd值则较小，且与l=2 mm时的Cd值几乎相同，这意味着l=20 mm的小孔呈现明显的薄孔和厚孔两种特性.

图5 小孔流量系数随水力直径的变化Fig.5 Evolution of the discharge coefficient with the hydraulic diameter

2.3 薄孔和厚孔两种特性分析

通过上述分析可以看出，小孔排液呈现薄孔和厚孔两种特性.为了深入分析这两种特性的影响，这里对小孔流量系数几何参数的综合影响和流动机理进行讨论.我们知道，影响小孔流量系数的三个几何参数（水头高度h、厚度l和水力直径d）并未独立，而是存在耦合影响.事实上，从量纲分析得出的小孔流量系数计算公式(11)可以看出，利用h/d，l/d和Re这三个无量纲数更能反映这些耦合影响.

从图4 可知，当h≥200 mm(l/d≈2)时，小孔流量系数可以认为不受水头高度影响.此时，小孔流量系数Cd仅与l/d和Re这两个无量纲数有关，如图6所示.为了便于讨论，这里的水头高度取为200 mm.可以认为，小孔的流量系数以l/d≈2或Reynolds 数Re≈9 600为界限取为两种定值，即

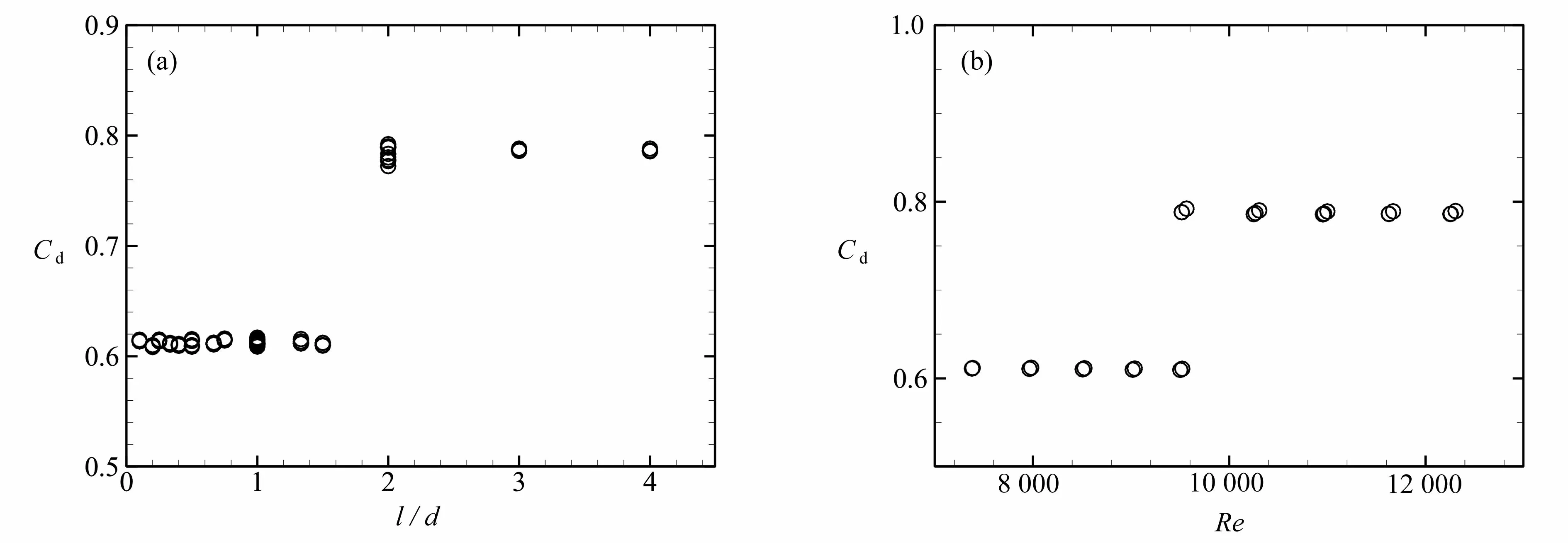
图6 h/d≥40时小孔流量系数随厚径比l /d和Reynolds 数R e 的变化：（a）厚径比l/d；（b）ReFig.6 Evolution of the discharge coefficient with thickness to diameter ratio l /d and Reynolds number R e for h/d≥40:（a）thickness to diameter ratio l/d；（b）Re

在重力作用下，液体进入排液孔时压力下降.在锐角小孔入口处，流体发生流动分离，产生分离剪切层，进而在拐角下游形成回流区.当厚径比l/d较小时，如l/d=0.4的薄孔，小孔内部的压力未得到恢复，液体便流出小孔，如图7(a)所示；当厚径比较大时，如l/d=2的厚孔，沿着小孔侧壁的压力得到恢复，液体发生再附现象，如图7(b)所示.这里，水头高度取为200 mm.对比图7(a)和图7(b)可以看出，当液体流经厚径比较小的排液孔时，压力损失较大，流量系数较小；当液体流经厚径比较大的排液孔时，压力损失则较小，流量系数较大.

图7 利用流线和压力云图描述的小孔附近流动拓扑结构：(a)l/d=0.4；(b)l/d=2Fig.7 The flow topology near the orifice of plotted streamlines and contours of pressure:(a)l/d=0.4;(b)l/d=2

为了深入认识薄孔和厚孔内部压力损失差异的机理，有必要对小孔入口处的分离剪切层失稳过程进行分析.剪切层的失稳过程与剪切层的增长密切相关，剪切层增长率可以用其涡量厚度δω来描述[21].这里，δω的定义为

其中，U1和U2分别为剪切层两侧的平均流向速度，(∂U/∂r)max表示沿排液孔径向的最大流向速度梯度.图8 给出了薄孔和厚孔中分离剪切层的涡量厚度分布.可以看出，在剪切层的初始演化阶段，厚孔的剪切层增长较快，增长率约为0.16.由于剪切层的快速增长，使得厚孔内部的分离剪切层失稳早于薄孔，进而导致厚孔内部的压力得到恢复.

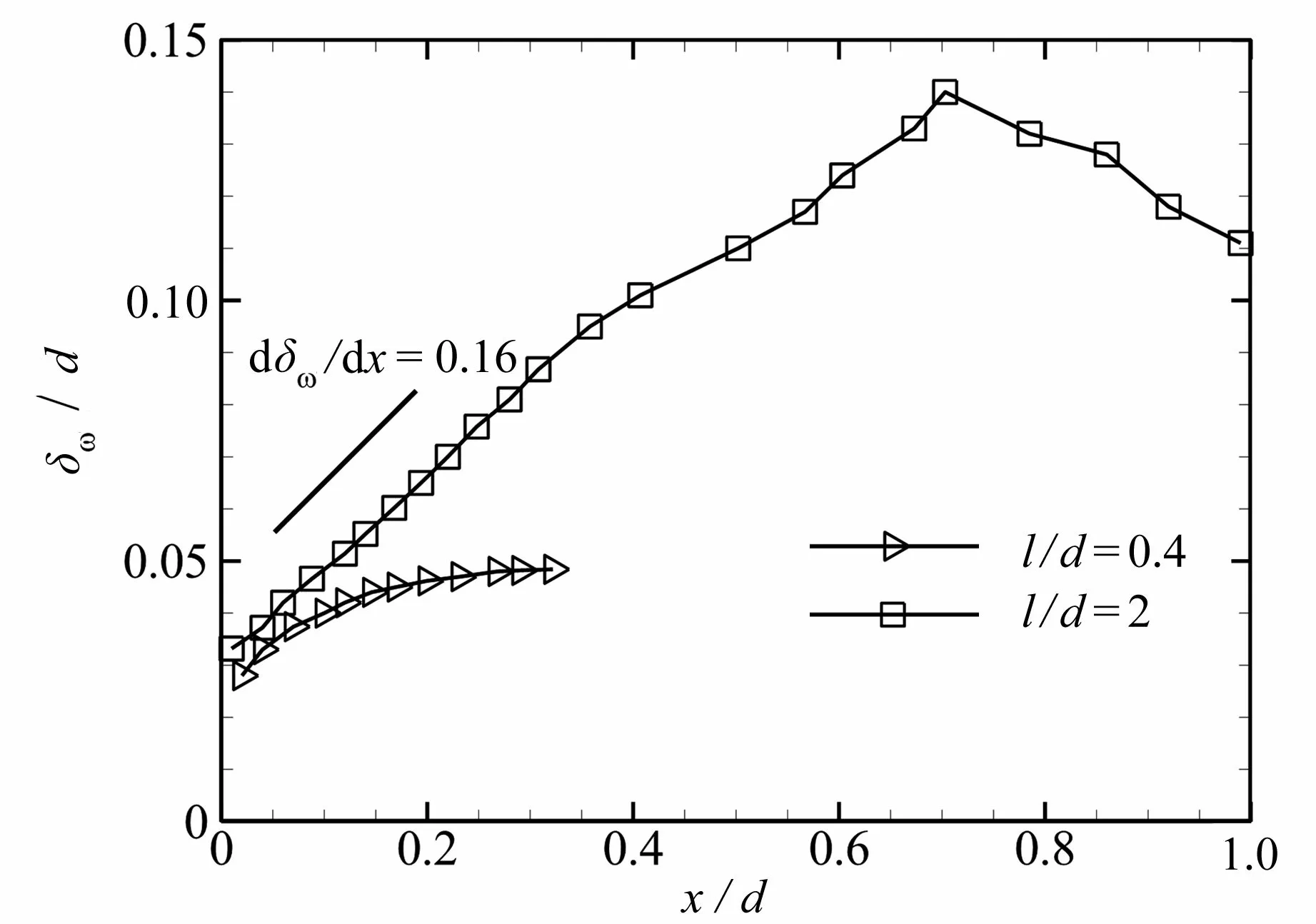
图8 涡量厚度沿分离剪切层的分布Fig.8 Distribution of the vorticity thickness along the separated shear layer

2.4 小孔流量系数的预测公式

上文已经得到了排液孔流量系数与三个无量纲参数的关系式(11).这里，利用数值模拟数据对不同工况下的排液孔流量系数进行公式拟合.由于影响排液孔流量系数的因素较多，也就是说流量系数公式中的自变量较多.因此，小孔流量系数的计算公式采用非线性曲线拟合较为合适：

式中，αi和βi(i=1,2,3)均为待定系数，这些系数可以由本文数值计算的数据求出.当l/d<2，且水头高度h<200 mm 时，根据数值计算数据可以求得

因此，式(14)可以写成

当l/d<2，且水头高度h≥ 200 mm 时，根据数值计算数据可以得出

式(14)可以写成

为了对式(18)进一步分析，这里对公式右边第一、二和三项分别标记为Iterm1，Iterm2，Iterm3，显然这些项均大于零.需要注意的是，本文考察的小孔直径最大为20 mm.结合式(18)的适用条件，即h≥ 200 mm，l/d<2，可以得出h/d>10.因此，这三项具有如下关系：

因此，可以合理把式(18)改写成Cd≈0.61，这与上文给出的结论一致，见式(12).

3 结论

本文利用VOF 方法对封闭腔体流动进行模拟，获取了排液孔的流量系数.采用控制变量法研究了水头高度、水力直径、小孔厚度对小孔流量系数的影响，并拟合了计算小孔流量系数的经验公式.通过对数值结果的分析与讨论，得出了如下结论：

1)当h<200 mm时，小孔流量系数随水头高度的增加而减小；当h≥200 mm 时，小孔流量系数几乎保持一个定值，约为0.61.

2)小孔流动存在薄孔和厚孔两种流动特性：当l/d<2时，小孔厚度呈现为薄孔特性，流量系数约为0.6；当l/d≥2时，小孔厚度为厚孔特性，流量系数约为0.8.

3)当h≥200 mm时，小孔流量系数不受水头高度影响.此时，小孔流量系数Cd仅与l/d和Re这两个无量纲数有关，小孔的流量系数以l/d≈2或Re≈9 600为界限取为两种定值.