高Re数层流管道中颗粒聚集特性的数值研究*

刘唐京，王企鲲，邹 赫

（上海理工大学 能源与动力工程学院，上海 200093）

引言

均匀的稀释悬浮液以层流方式通过直圆管时，流体中的刚性球形颗粒最终会迁移到半径约为0.6R（R为管道半径）的圆环上，这个环也被称为Segre-Silberberg 环[1].这表明颗粒在随流体运动时，除受到主流方向的驱动力外，在径向上还受到一个升力使得颗粒发生迁移.这个径向上的升力是由于运动流体的惯性引起的，因此又被称为“惯性升力”，由其“惯性升力”而引发的颗粒聚集现象称为“惯性聚集”[2-3].

这种现象是在低Re数（Re为Reynolds 数）下管道流中发现的，之后有学者在高Re数流中也发现了颗粒的惯性聚集现象.Matas 等[4]对高Re数下悬浮粒子在Poiseuille 流中的“惯性聚集”进行实验研究，得到了不同Re数下管道直径与颗粒直径比在8～42 范围内颗粒的聚集位置.Morita 等[5]通过实验发现，Re数在1 000范围内的稀释悬浮液通过直圆管时，只有一个稳定的聚集点.由于实验很难获取流场中的各项力学参数，随着数值模拟（CFD）在流体力学中的广泛运用[6-8]，一些学者为了揭示颗粒所受惯性升力的形成特性，通过数值计算方法对颗粒的“惯性聚集”进行了研究[9-10].但由于流动是非定常的，计算模型的数学描述比较困难，Carlo 等[11]首次提出“相对运动模型”，将原本的非定常问题转化为准定常问题.基于相对运动模型，王企鲲[12-13]对方管中颗粒的受力特性进行了数值研究，揭示了颗粒聚集的力学成因并归纳出颗粒稳定聚集点的水动力学判据.

相对运动模型的提出，极大地简化了计算模型.但采用相对运动模型进行数值模拟时，为了使流动达到充分发展状态，一般需要预留L=0.058Re·D（D为管径）[14]的管长以消除入口段的影响.这在计算高Re数工况时就需要非常长的管道，造成网格数量大，使得数值计算变得困难.考虑到管内流动属于周期性流动，因此本文对管道进、出口设置周期性边界条件，解决了高Re数工况下管道较长的问题，同时计算高Re数管流中颗粒惯性聚集的受力特性.

1 计算模型与计算方法

1.1 计算模型

本文考虑单个刚性球形颗粒在直圆管Poiseuille 流中运动，管道直径为D，长度为L，小球直径为d，如图1所示.目前比较常用的模型是6 自由度模型，然而这种计算模型是非定常的，模型的数学描述比较复杂，并且计算过程繁琐也很耗时，此外6 自由度模型虽然能获得颗粒的运动轨迹，但无法获取颗粒升力在通道内的空间分布规律.本文采用的相对运动模型是在6 自由度模型的基础上进行简化，它虽然无法获得颗粒的运动轨迹，但能计算出颗粒在通道内的受力特性.通过分析受力特性来确定颗粒的聚集点，这在文献[11-13]中给出了比较详细的讨论.

图1 计算模型示意图Fig.1 The sketch for the numerical model

相对运动模型是通过创建一个惯性坐标系将颗粒的平移速度转移给管壁，使得计算时的流场为准定常，从而简化计算.即将计算坐标系设置在颗粒的中心（如图1所示）并随颗粒一同平移，则在此惯性坐标系下，颗粒的平移速度为零，仅存在以原点为中心的旋转速度，管壁则以颗粒的速率反向移动.

1.2 计算方法

本文基于有限体积法进行三维数值模拟，求解稳态Navier-Stokes 方程，其控制方程如式（1）所示.流动介质为常温常压液态水，考虑到颗粒是悬浮颗粒，取其密度与水相同，为ρ=1 000 kg/m3.在CFD 计算中，采用双精度来进行计算，压力与速度的耦合采用coupled 算法，压力方程的离散采用二阶格式，动量方程的离散采用三阶精度的QUICK 格式[14-15]：

式中，u为平移坐标系Oxyz中流体的相对速度，p为压强，ρ 和υ 分别为流体的密度和运动黏度.

在CFD 计算中，颗粒的平移速度UP被转化为管壁运动的边界条件，这里需要通过试凑的方式来获得颗粒在该位置的最终恒定运动速度.首先假定一个速度UP0进行试算，输出颗粒在沿流动方向（x方向）上的合力Fx0，在一定精度内，判断合力是否为零（零指的是零量阶，不是数值上为零）；若不为零则需不断地迭代更新壁面速度，直到颗粒在流动方向上合力为零.同时，颗粒的旋转速度也用同样的方式进行试凑，直到颗粒在所有方向上转矩为零.此时，颗粒在y方向上所受的力便为径向升力.

为了提高计算效率，平移速度的初始参考值为UP=2U[1−(r+)2]，旋转速度的初始参考值为对于UP和ω 的更新，本文利用具有超线性收敛性的“割线法”更新下一步迭代数据，分别由式（2）、（3）计算，采用这种方法通常试凑3 至4 次就能得到结果，而试凑一次也只需迭代150 次左右：

式中，UPn和ωPn分别为平移速度和旋转速度，Fxn和MPn分别为阻力和转矩，n=0,1,2.

颗粒的升力Fy和阻力Fx分别按式（4）、（5）计算：

式中，i和j分别为x方向和y方向的单位向量，P为应力张量，n为颗粒表面外法线单位向量，dS为面积微元，Σ 为颗粒表面.

颗粒的转矩按式（6）计算：

式中，r为由颗粒中心指向颗粒表面的矢径.

在CFD 计算中，当对管道进、出口采用周期性边界条件时，计算区域内的每一处压力分为周期性压力和线性压力，而在CFD 实际的计算过程中只显现出周期性压力少了线性压力，因此真实的压力应为：preal=p+β∆x（p为周期性压力，β为一个周期内的平均压力梯度，∆x=x1−x2）[14].那么，式(4)～ (6)在计算颗粒的升力、阻力以及转矩时未包含线性压力提供的那部分力.线性压力对颗粒贡献的升力、阻力及转矩由式(7)、(8)计算，从中可以发现，线性压力对颗粒提供的力只在流动方向上，并且对转矩的贡献为零，也就是说线性压力只对颗粒的阻力有影响：

式中，I为单位二阶张量.因此颗粒在流向上的实际阻力为

为了方便下文的讨论与分析，本文定义如下无量纲参数：

升力系数CFL为

式中，d为颗粒直径，D为管道直径.颗粒的无量纲直径为

颗粒无量纲径向位置为

式中，r为管中心与颗粒球心的距离，R为管道半径.Re数为

式中U为管内流体的平均速度，µ为流体的动力黏度.扰动强度为

式中，v和w分别为y方向和z方向的流速分量.

2 结果与讨论

2.1 网格无关性验证

本文采用结构化网格对计算域进行网格划分，如图2（a）所示.为了提高计算的稳定性和精度，在流体与颗粒间的边界层网格进行了加密处理，如图2（b）所示.为了保证计算的准确性和经济性，以及获得颗粒的真实受力，本文先对网格无关性进行了验证.本次验证的计算工况为：a+=1/9，颗粒的径向位置r+=0.1，管长L=4D.

图2 网格示意图：（a）管道网格；（b）颗粒周围网格Fig.2 Schematic diagrams of the grids:a）pipeline grid;b）grids around particle

从图3 中可看出，当网格数量达到50 万左右时，颗粒的升力系数基本保持不变，考虑到在满足计算精度的同时尽可能节约计算时间，本文最终确定计算域的网格数量控制在60 万左右.对于下文采用不同管长计算的工况，网格划分将以本次验证的管道网格为基准，网格尺寸保持一致.

图3 网格无关性验证Fig.3 Grid independence verifications

2.2 周期性边条的可行性分析

在低Re数下，文献[2-13]基于相对运动模型，边界条件为进口给定均匀的相对速度，出口为压力出口.而在高Re数下，这种边界条件通常需要很长的管道才能计算出可靠的结果，因此考虑采用周期性边界条件来减小管长.为了验证周期性边界条件的可行性，本文对Re=350，a+=1/9 的工况进行了数值模拟.本次模拟分别选取管长L=4D和L=50D的管道，L=4D的管道对进、出口采用周期性边界条件，L=50D的管道则与文献[13]采用相同的边界条件，模拟结果如图4所示.

由图4 可知，两种边界条件得到的升力系数曲线完全重合，升力系数为零且该点一阶导数小于零的点即为颗粒的稳定聚集点，因此Re=350 时a+=1/9 的颗粒主要聚集在r+≈0.76 处.而文献[4]的实验结果为r+≈0.77，两者比较吻合，这说明周期性边界条件是可行的.当Re=350 时，对进、出口采用周期性边界条件只需4 倍管径长度的管道便可计算出结果，而用文献[13]中的边界条件却需要50 倍管径长度.因此在求解高Re数流中颗粒的惯性聚集时，采用周期性边界条件可以有效地减小管长，降低计算量.

图4 不同边界条件的模拟结果Fig.4 Simulation results under different boundary conditions

2.3 周期长度的确定

当计算高Re数工况采用周期性边界条件时，需知道管长L（周期长度）为多少时，获得的计算结果才真实可靠.针对这个问题，本文采用不同周期长度的管道对无量纲直径a+=1/9 的颗粒进行了模拟分析，Re=350.

从图5 中可看出，当L≥3D时，随着周期长度的增加，计算结果将保持不变，并且与实验结果是吻合的（2.2 小节中已做对比），这从力的角度来看L=3D的管道便可以得到稳定的计算结果.在相对运动模型中，颗粒是相对静止的，这会对管中的流体产生扰动，而较短的周期长度有可能会使这种扰动延伸到边界上，影响计算结果.而且这有可能会出现不同周期长度得到相同的升力分布，但流场却不一定是相同的情况.为了确保计算结果的可靠性，本文对不同周期长度颗粒附近以及靠近进、出口处的扰动强度进行了对比，如图6所示.考虑到越靠近壁面，颗粒对流体造成的扰动越强，因此本文选取颗粒靠近壁面（r+=0.8）的工况进行对比.

图5 不同周期长度下的升力分布Fig.5 The lift distribution under different period lengths

从图6 中可以发现，随着周期长度的增加，靠近管道进、出口处的扰动强度是不断减小的，当L≥4D时，靠近进、出口处的扰动基本可以忽略不计.这说明当周期长度大于4D时，流场将不会在发生变化，结合上文升力分布结果，对于Re=350 的工况，L=4D是可行的计算周期.而对更高的Re数，本文也进行了验证，结果如图7所示.当Re数达到800 时，计算结果也符合：1）靠近管道进、出口处扰动强度为零；2）颗粒的聚集点与文献[4]的实验结果相符.因此，对于Re<1 000、a+≤1/9 的工况，本文确定4D为计算周期.

图6 不同周期长度下的扰动强度对比：（a）L=2D；（b）L=3D；（c）L=4D；（d）L=5DFig.6 Comparisons of disturbance intensities under different period lengths:a）L=2D;b）L=3D;c）L=4D;d）L=5D

图7 Re=800 的计算结果：（a）升力分布；（b）扰动强度Fig.7 Calculation results for Re=800:a）lift distribution;b）disturbance intensity

2.4 周期性边条的应用

2.4.1Re<1 000

前文对周期性边条的可行性进行了验证，并对Re<1 000 工况给出了一个可行的计算周期为L=4D.在此基础上，本文在这里对不同粒径的颗粒进行了数值模拟，研究不同Re数下颗粒的受力特性以及对颗粒聚集点的影响.

如图8所示，在低Re数下，颗粒在径向上升力分布是类抛物线，不同大小的颗粒主要聚集在r+=0.6 ～0.7 之间，与管壁有一定的距离.而随着Re数的增大，颗粒的升力分布以及聚集点都出现了明显的变化.主要表现如下：高Re数下颗粒的升力不再呈类抛物线分布，颗粒受到的升力具有一定的波动，在r+=0.5 ～ 0.7 之间出现一段升力相对较小区域，而在这个区域内有出现第二个聚集点（内环）的趋势.此外，随着Re数的增大，颗粒主要聚集在r+=0.75 ～ 0.85 之间（外环），向着壁面靠近.即Re数越大，颗粒的聚集位置越靠近壁面；而与颗粒粒径的关系则与之相反，粒径越大，聚集位置越向着管中心迁移.

图8 不同Re 下颗粒的升力分布：（a）Re=50；（b）Re=350；（c）Re=500；（d）Re=800Fig.8 The lift distribution of particles under different values of Re:a）Re=50;b）Re=350;c）Re=500;d）Re=800

在本次的计算结果中，只发现了一个稳定聚集点，这与Morita 等[5]的实验结果是一致的，当Re<1 000 时，如果管道足够长，内环将消失，所有的粒子都将聚集在外环上.而在Matas 等[4]的实验中，他们在管道的上游区域发现了内环的存在，但在下游区域观察到内环上的颗粒有向外环迁移的趋势.本文认为这可能是Matas 等[4]实验的管道不够长，颗粒的迁移未完全发展，颗粒要脱离r+=0.5 ～ 0.7 这个升力相对较小的区域需要较长的时间.

2.4.2Re≥1 000

从图8 的升力分布来看，在更高Re数下有可能出现第二个稳定聚集点.为了探究Re≥1 000 时是否有第二个稳定聚集点的出现，本文选用了a+=1/17 的颗粒进行模拟.

本次模拟仍是用L=4D的管道进行计算，首先对周期长度的可靠性进行验证，结果如图9（a）所示.从其扰动强度来看，4 倍管径周期长度符合计算精度，且颗粒的升力分布与上文中高Re数的分布特征一样.因此本文认为对于Re≤1 600，a+=1/17 的工况，L=4D的管道依然是可行的.

从图9（b）颗粒的升力分布可以发现，当Re数达到1 200 时，a+=1/17 的颗粒在径向上有三个聚集点，其中有两个是稳定聚集点，分别在r+≈0.63，0.87 处.这说明当Re>1 000 时，对于小粒径的颗粒是有可能存在两个稳定聚集点的.由于大粒径的颗粒在Re数达到1 000 时计算不稳定，所以对于更大粒径的颗粒本文没有继续进行深入研究.

图9 a + =1/17，Re≥1 000 的计算结果：（a）Re=1 600 时的扰动强度；（b）升力分布Fig.9 The calculation results of a+ =1/17,Re≥1 000:a）the disturbance intensity at Re=1 600;b）the lift distribution

2.5 流场分析

为了探究低Re数和高Re数下管内颗粒惯性升力分布不同的原因，本文对颗粒所在横截面（即x=0 截面）的流场进行了分析，以a+=1/9 的颗粒为例，如图10 ～ 12所示.图10 ～ 12 分别为r+=0.4，0.6，0.8 时不同Re数下z方向的速度云图和该截面上的速度矢量图，对z方向的速度无量纲化为.

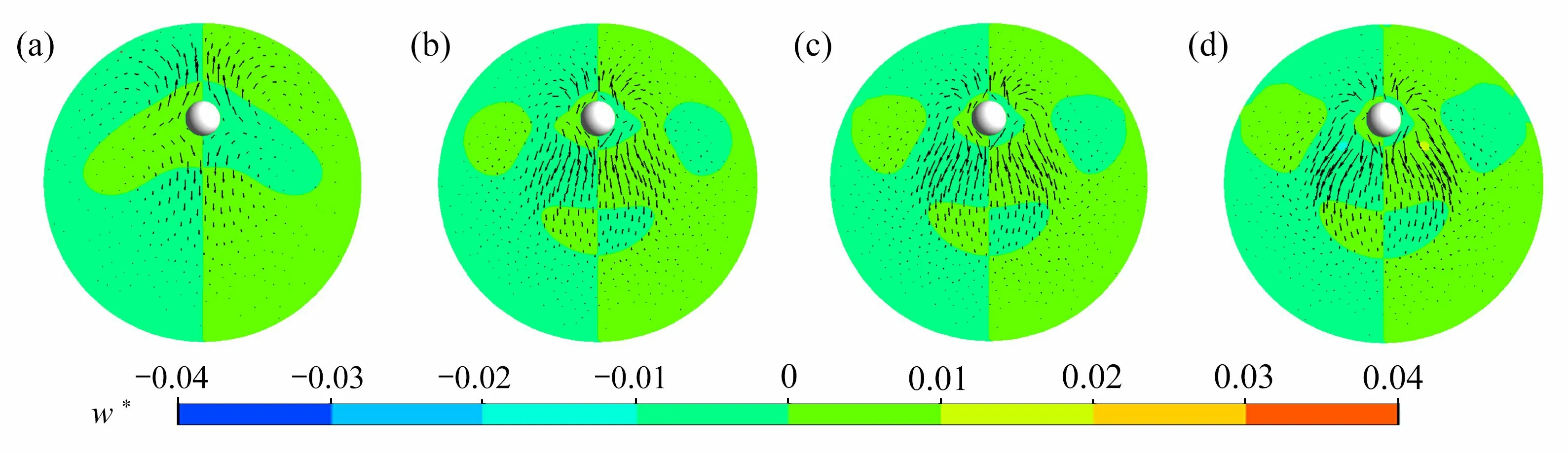
图10 x=0 截面的速度云图和矢量图（r+ =0.4）：（a）Re=50；（b）Re=350；（c）Re=500；（d）Re=800Fig.10 Velocity contours and velocity vectors of section x = 0r+ =0.4）:a）Re=50;b）Re=350;c）Re=500;d）Re=800

图12 x=0 截面的速度云图和矢量图（r+ =0.8）：（a）Re=50；（b）Re=350；（c）Re=500；（d）Re=800Fig.12 Velocity contours and velocity vectors of section x = 0r+ =0.8）:a）Re=50;b）Re=350;c）Re=500;d）Re=800

从图11、12 可以明显地看出，在颗粒的周围有二次流产生，而二次流可能会对颗粒的升力造成影响.从速度云图及矢量图来看，当Re=50 时，颗粒周围并没有明显的二次流动，尤其是颗粒更靠近通道中心时，但随着颗粒向壁面靠近，可以发现有微弱的二次流产生.然而当Re≥350 时，即使颗粒更靠近通道中心也会有微弱的二次流产生，且随着Re数的增大以及颗粒向壁面靠近，二次流变得越来越强烈.此外从速度矢量图可以发现：在低Re数时，二次流主要向着颗粒的下方流动；而在高Re数时，二次流在颗粒靠近通道中心时先是向颗粒下方流动，而后随着颗粒向壁面靠近以及Re数的增大，其逐渐向颗粒左右两侧流动.

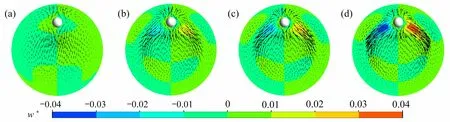
图11 x=0 截面的速度云图和矢量图（r+ =0.6）：（a）Re=50；（b）Re=350；（c）Re=500；（d）Re=800Fig.11 Velocity contours and velocity vectors of section x = 0（r+ =0.6）:a）Re=50;b）Re=350;c）Re=500;d）Re=800

对此本文认为，由于颗粒周围二次流的影响，颗粒在径向上的升力分布才出现图8所示的变化.在低Re数时，二次流主要向颗粒下方流动且其强度随着颗粒靠近壁面而增大，这会给颗粒一个向下的力，而在图8中也能明显地看到在靠近壁面时升力下降得更快，这说明二次流对颗粒的升力是有影响的.在高Re数时，颗粒所受升力在r+=0.4 ～ 0.7 之间相对平缓且升力系数较小，这与前文所说的二次流强度随颗粒径向位置变化相对应.而在Re≥500，r+=0.75 时升力出现回升，本文认为这是由于二次流流向变化所引起的，在r+=0.8 时，二次流主要向颗粒两侧成对称流动，这使得其对升力的影响减弱.

3 结论

Carlo[2]提出的相对运动模型在求解低Re数下颗粒的惯性聚集是比较成熟的.但在高Re数下，如果仍对进口给定均匀流，为了消除入口段的影响需要很长的管道，造成网格数量大，计算成本高，因此本文尝试对管道进、出口采用周期性边界条件以减小计算域管长.本文主要对周期性边界条件的可行性进行了验证并求解了高Re数下颗粒受力特性，得到了以下结论：

1）在求解高Re数流的惯性聚集，周期性边界条件的使用可以有效地减小管长，这很大程度上提高了数值计算的效率以及经济性.当Re<1 000 时，a+≤1/9 的颗粒用4D周期就可以计算出可靠的结果.对于粒径细小的颗粒，如文中a+=1/17 的颗粒，4D周期可计算的Re数高达1 600.

2）在低Re数下，颗粒在径向上的升力呈抛物线分布，且颗粒主要聚集在离壁面较远的区域.随着Re数的不断增大，颗粒的聚集位置向着壁面靠近，且其升力分布出现了较大的波动，它将不再呈类抛物线分布，在r+=0.5 ～ 0.7 之间出现了一段升力相对较小的区域，而在这个区域内有出现新聚集点的趋势.

3）当Re≤1 000 时，本文只发现了一个聚集点，新的聚集点并没有出现.但当Re>1 000 时，本文用a+=1/17 的颗粒进行计算得到了两个稳定的聚集点，这说明在高Re数流中小粒径的颗粒有可能出现两个稳定的聚集点.

4）颗粒周围有二次流的产生，其强度随着Re数的增大而增大，且随着颗粒越靠近壁面，二次流的强度也会增加.在低Re数时，二次流主要向着颗粒的下方流动；而在高Re数时，二次流在颗粒靠近通道中心时先是向颗粒下方流动，而后随着颗粒向壁面靠近以及Re数的增大，其逐渐向颗粒左右两侧流动.而受二次流的影响，颗粒所受升力在高Re数和低Re数呈现不同的空间分布规律.