高速列车车顶–升力翼组合体气动特性

高建勇，张军,*，倪章松，周鹏，朱彦，王成强，高广军

1.成都流体动力创新中心，成都 610072

2.中车长春轨道客车股份有限公司，长春 130062

3.中南大学交通运输工程学院 轨道交通安全教育部重点实验室，长沙 410075

0 引言

中国高速列车运行速度不断提高，目前“复兴号”运行速度已达350 km/h。若高速列车在400～500 km/h 速度区间运行，还能进一步缩短城市群通行的时空距离。为在提升列车运行速度的同时降低整体能耗和全生命周期成本，有学者提出在列车车顶布置升力翼提供升力，以达到等效减重的目的。

王瑞东等[1]针对升力翼进行了翼型的优化设计及布局初步设计，使翼型升力系数上升了14.06%。国内外学者对翼型的气动特性开展了大量研究。Sheldahl 等[2]通过风洞试验测试了7 种标准翼型在0°～180°迎角下的气动力，给出各翼型升力系数随迎角的变化情况。McAlister 等[3]在风洞中对二维和三维NACA0015 翼型表面压力分布、速度分布等进行了研究。Joslin 等[4]对风洞环境下的NACA0015 翼型进行了数值仿真研究，并与试验结果进行了对比，指出两者的差异主要是由翼型的气流分离位置差异所导致。Lee 等[5]对不同迎角下NACA0015 翼型的气动特性进行了数值仿真研究，发现该翼型在10°以上迎角即出现失速现象，还讨论了数值仿真中y+值对升力、压力的影响。Ahmed 等[6]在风洞中对二维NACA4412 翼型在不同迎角、不同飞高（升力翼与车顶之间的距离）时的升力和阻力变化规律进行了研究，发现翼型在各迎角下靠近地面都会导致上表面的吸力损失。Singh[7]采用JavaFoil 对几种翼型在来流马赫数Ma=1 条件下的气动特性进行了研究，得到了气动特性较优的翼型。Gerakopulos 等[8]对低雷诺数下NACA0018 翼型的气动特性进行了试验研究，详细分析了不同迎角下的翼型升力线变化。

升力翼气动特性直接影响高速列车等效减重效果。本文采用数值仿真方法对飞高、来流速度、迎角等设计参数，以及车–翼连接杆对升力翼气动性能的影响进行研究，为高速列车升力翼设计及其风洞试验方案提供参考。

1 数值计算模型

1.1 流动控制方程

在直角坐标系中，三维可压缩黏性流体运动可由控制方程描述[9-12]。连续性方程为：

动量方程：

能量方程：

湍动能方程：

湍动能耗散率方程：

式中：µt=ρcµε2/k 为湍流黏性系数；cµ、c1、c2、σk、σε为常数；ρ为气体密度；µ为动力黏性系数；k 为湍动能；ε为湍动能耗散率；U为模型周围流场速度矢量；ui、uj为速度分量；Gk=0.5(∂ui/∂xj+∂uj/∂xi）；R 为摩尔气体常数；焓h=e+0.5U2+p/ρ，e 为内能，p 为压强。

1.2 气动仿真模型

仿真模型由翼型、车–翼连接杆和简化车顶组成。翼型弦长C=500 mm，展长为7C。简化车顶模型高1.2C，长9.6C，前后缘为圆角；车–翼连接杆为等截面直杆，横截面采用NACA0012 翼型，宽0.5C；升力翼和车顶之间的距离定义为飞高H。图1 和2 分别给出了模型的主要尺寸和计算域几何参数。计算域宽44C，高18C；其入口距离模型12C，出口距离模型18C，两侧距离模型9C。

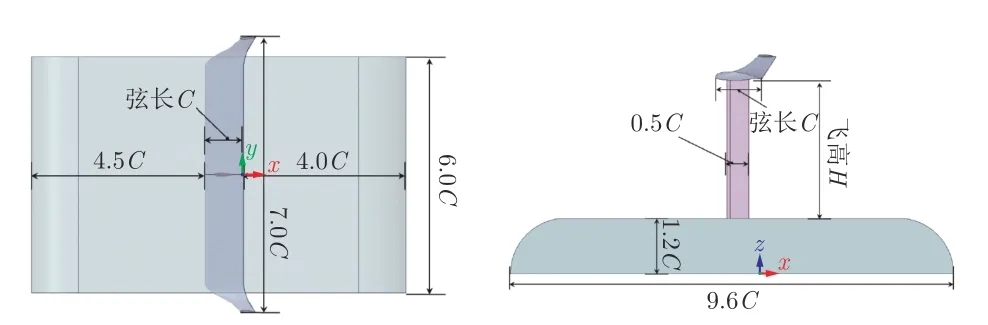
图1 模型尺寸Fig.1 The size of model

图2 计算域Fig.2 Computational domain

计算域内网格尺寸在0.1～500.0 mm 范围内，升力翼和车–翼连接杆表面网格尺寸在0.2～8.0 mm范围内；车顶面网格最大尺寸为40 mm，地面网格最大尺寸为100 mm；计算域入口和出口网格最大尺寸为250 mm，两侧和顶面网格最大尺寸为500 mm。图3 为网格分布示意图。

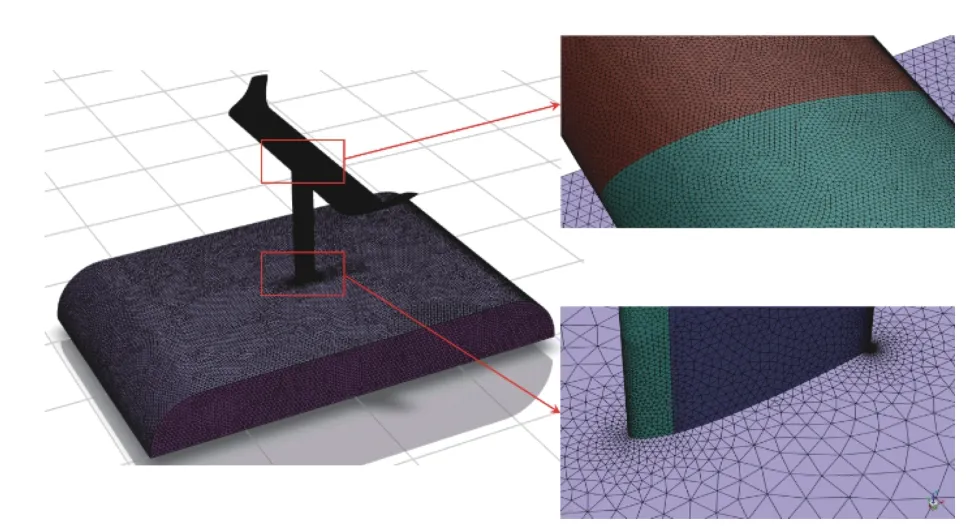
图3 网格分布Fig.3 Mesh distribution

为获得准确的气动数据，在升力翼、车–翼连接杆和地面附近分别建立密度盒，并建立一个包裹升力翼和车–翼连接杆的大密度盒，如图4所示。空间网格最大尺寸为500 mm，在计算域地面、简化车顶、车–翼连接杆和升力翼的表面添加10 层边界层网格，网格第一层高度为0.3 mm，增长率为1.2；空间体采用六面体网格。计算域入口和出口采用压力远场，给定马赫数；为模拟真实风洞环境，计算域地面、两侧和顶面均采用固定壁面；车顶、升力翼和车–翼连接杆同样采用固定壁面。

图4 空间密度盒Fig.4 Density box

采用压力基求解稳态流场，湍流模型选择Realizable k–ε模型，增强壁面函数。求解方法中，速度压力耦合选择SIMPLE 格式；空间离散格式中，压力选择Standard 格式，密度、动量、湍动能、湍流耗散率及能量采用Second Order Upwind 格式[13-14]。

在自由来流条件下，本文对单个翼型在不同迎角下的气动力进行了数值仿真，并与NASA 风洞试验结果[15]进行对比。具体研究工作可参阅文献[1]。

1.3 空间网格无关性验证

为保证计算结果不受网格影响，通过改变空间密度盒内网格的最大尺寸，建立了粗、中、细等3 种不同尺寸的网格模型，其网格量分别为3.16×106、4.57×106和7.56×106。网格模型具体数据见表1。

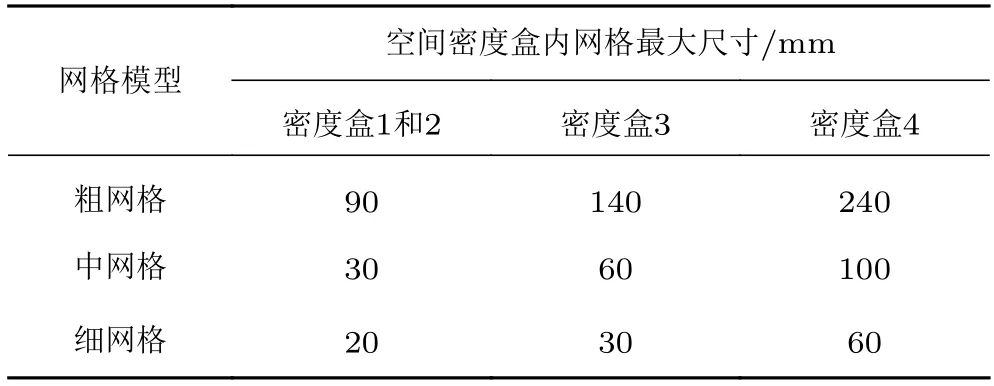
表1 密度盒网格尺寸Table 1 Density box mesh size

来流速度v=110 m/s 时，以数值方法分析各网格模型下的升力翼气动力。在粗、中、细网格模型下，升力翼升力分别为10 144.4、10 859.1 和10 862.5 N。与细网格模型相比，中、粗网格模型计算升力的误差分别约为6.61%和0.03%，故后文均采用中网格模型进行升力翼气动特性研究。

2 仿真结果与分析

使用有车–翼连接杆模型和无车–翼连接杆模型（无车–翼连接杆模型即移除车–翼连接杆、仅保留升力翼及简化车顶的模型），对不同迎角α、不同来流速度v、不同飞高H 的升力翼气动特性进行仿真研究，研究工况如表2所示（共计54 组工况）。

表2 仿真工况Table 2 Numerical simulation case

2.1 升力翼周围的流场特征

为分析升力翼基本流场特征，图5 和6 给出了模型纵向对称面的速度和压力分布云图（v=140 m/s，H=3C，α=12°）。在简化车顶的上游和下游，流场表现为高压低速；而在简化车顶的前缘和后缘倒角位置，流场表现为低压高速，前缘产生的低压高速气流还会使升力翼和连接杆局部区域的流场速度较来流速度偏大。升力翼上表面空间流场表现为低压高速，而下表面空间流场表现为高压低速；升力翼上表面气流在后缘附近分离，使后缘附近压力逐渐增大。

图5 纵向对称面速度云图Fig.5 Velocity nephogram of longitudinal symmetry plane

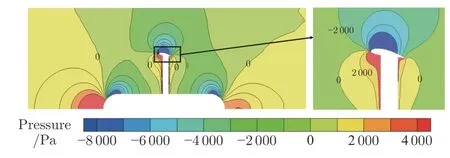
图6 纵向对称面压力云图Fig.6 Pressure nephogram of longitudinal symmetry plane

车–翼连接杆连接升力翼和简化车顶，同样对流场结构有较大影响。为明确车–翼连接杆对周围流场的扰动规律，将车顶上方1C、2C 和2.8C 处的水平面分别命名为Z1、Z2 和Z3，这3 个水平面内车–翼连接杆周围的速度和压力如图7所示（v=140 m/s，H=3C，α=12°）。

图7 车–翼连接杆不同高度的流场Fig.7 Flow field of train-wing connection rod at different heights

车–翼连接杆是横截面为NACA0012 翼型的等截面直杆，其周围流场受到升力翼和简化车顶的共同影响。连接杆两侧流场表现为低压高速，而其上游和下游则表现为高压低速。结合图5～7 可以看出：从Z1 平面至Z3 平面，车–翼连接杆周围的气流速度逐渐减小，一方面是由于简化车顶前缘上方的高速气流团的速度随着高度增大而减小，另一方面是由于升力翼下方出现一个低速气流团；在压力分布上，由于简化车顶上方表现为低压，升力翼下方表现为高压，故随着高度增大，连接杆两侧的压力逐渐增大，而连接杆上游和下游的低压区逐渐减小。

2.2 车–翼连接杆与升力翼的相互干扰

车–翼连接杆将升力翼的气动力传递至列车上，是升力翼系统的关键组成部分。但车–翼连接杆暴露在自由来流中，不可避免地会对升力翼气动特性产生一定影响。图8 为有/无车–翼连接杆工况下的模型纵向对称面速度流场，图9 为有/无车–翼连接杆的升力翼表面压力云图对比（v=140 m/s，H=3C，α=12°）。车–翼连接杆对升力翼的影响集中于升力翼下表面，由于车–翼连接杆周围气流速度比自由来流低，车–翼连接杆两侧空间表现为高压，使得升力翼和车–翼连接杆的连接位置周边压力局部增强。气流在车–翼连接杆后缘分离，车–翼连接杆后缘区域表现为正压；同时，在升力翼下表面高压区影响下，连接杆后缘区域尤其是靠近升力翼的部分表现为高压，而车–翼连接杆后缘中部区域则表现为低压。

图8 纵向对称面速度分布Fig.8 Velocity nephogram of longitudinal symmetry plane

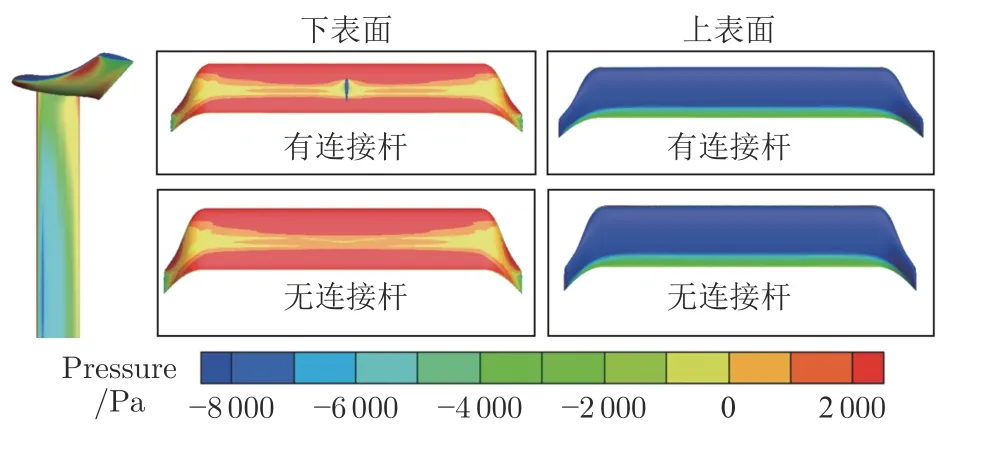
图9 模型压力云图对比Fig.9 Model pressure nephogram comparison

表3 和4 给出了H=3C 时不同迎角和来流速度下的升力翼升力系数和阻力系数。气动系数Cp为：

表3 升力翼升力系数Table 3 Lift wing lift coefficient

式中：F 表示相应的升力或阻力，v 为来流速度，ρ为空气密度，A 为参考面积。计算升力系数时，A 取垂直方向投影面积，约1.604 m2；计算阻力系数时，A 取来流方向的投影面积，约0.473 m2。

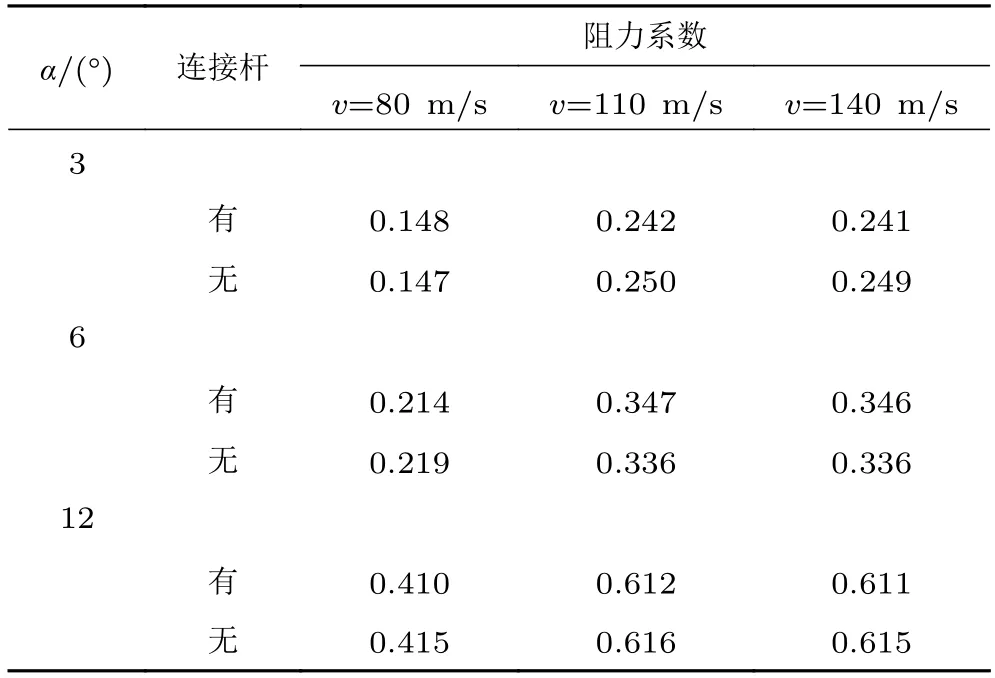
表4 升力翼阻力系数Table 4 Lift wing drag coefficient

从表3 和4 可以看出，车–翼连接杆对升力翼升力系数影响最大约0.03，对应的升力影响在3.7%左右；车–翼连接杆对阻力系数影响最大约0.01，对应的阻力影响在3.4%左右。这表明车–翼连接杆对升力翼气动性能影响很小，在对升力翼气动参数进行研究时，可不考虑车–翼连接杆的影响。在升力翼飞高为2C 和1C 时，车–翼连接杆对升力翼气动性能的影响类似。

2.3 升力翼飞高对气动特性的影响

表5 给出了α=12°时不同飞高和来流速度下的升力翼升力。从表5 可以看出，在不同来流速度下，随着升力翼飞高增大，升力有减小的趋势。与H=1C 时相比，H=3C 时的升力仅减小约3%，表明单个升力翼升力受飞高影响较小。从图7 可以看出，H=1C 时，升力翼周围气流速度比H=3C 时高，使得飞高较低的升力翼升力更大。升力翼上表面负压和下表面正压是升力的主要来源。图10 给出了不同飞高（1C 和3C）下的流场纵向对称面压力分布云图（v=110 m/s）。与H=3C 时的压力分布相比，当H=1C 时，升力翼上表面负压区和车顶负压区相连接，升力翼下表面正压区面积明显增大。

表5 升力翼升力Table 5 Lift force of lift wing

图10 不同飞高下的流场纵向对称面压力云图Fig.10 Pressure nephogram of longitudinal symmetry plane at different fly heights

2.4 来流速度对升力翼气动特性的影响

取来流速度v 在60～140 m/s 范围内，对有车–翼连接杆、H=3C、α=12°时的升力翼气动力进行仿真研究，得到气动系数随v 的变化规律。图11 为不同来流速度下的升力翼升力系数和阻力系数变化情况。随着v 增大，升力系数先增大后减小，当v 达到90 m/s 以上时，升力系数稳定在1.62 左右；阻力系数随速度增大而增大，当v 达到90 m/s 以上时，阻力系数稳定在0.61 左右。

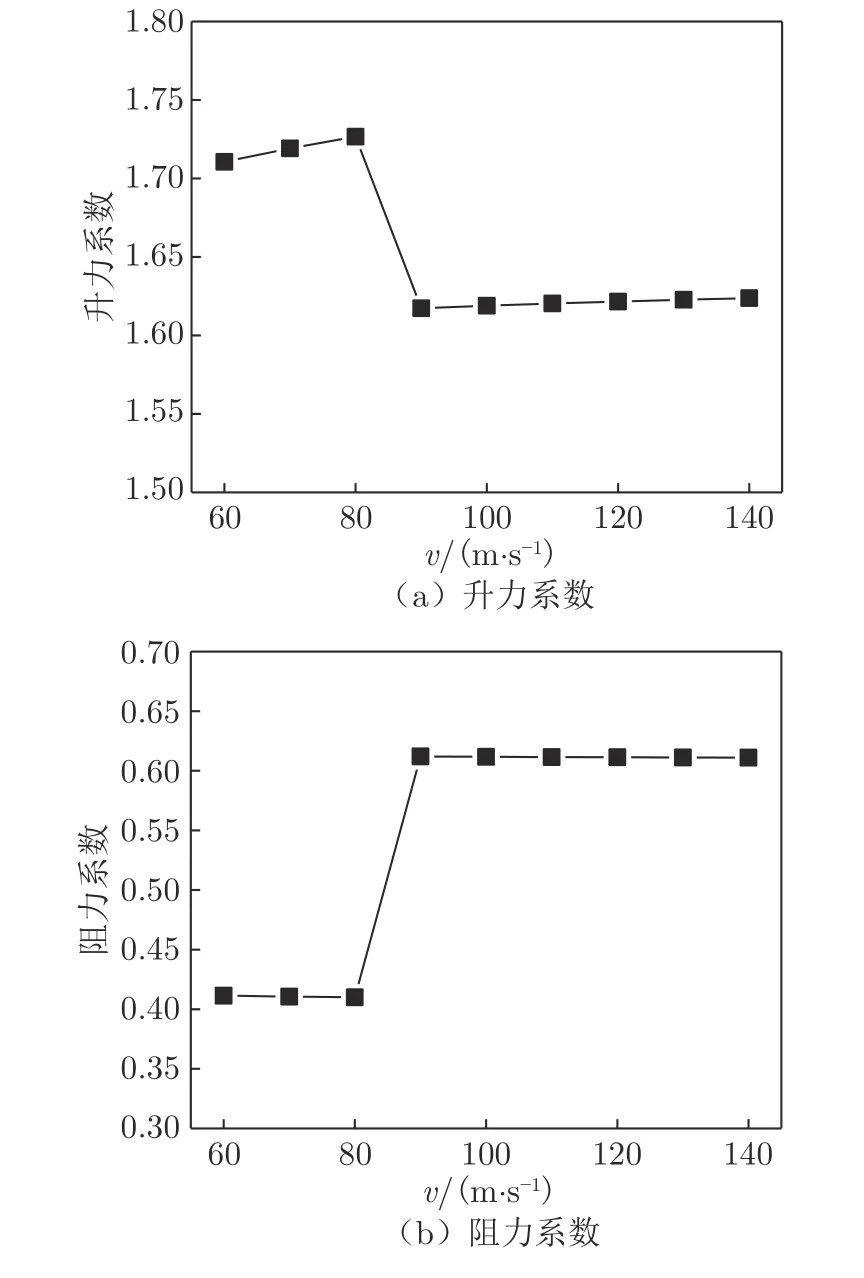
图11 升力翼气动系数随速度的变化Fig.11 Variation of aerodynamic coefficients of lift wing with velocity

值得注意的是，当v 从80 m/s 增大至90 m/s，升力系数迅速减小，而阻力系数迅速增大。为分析气动系数变化原因，在图12 中进行了升力翼气流分离点对比：当v=90 m/s 时，升力翼上表面尾缘的气流分离点比v=80 m/s 时有所提前。气流提前分离，使该区域出现吸力损失，从而导致升力翼升力系数减小和阻力系数增大。

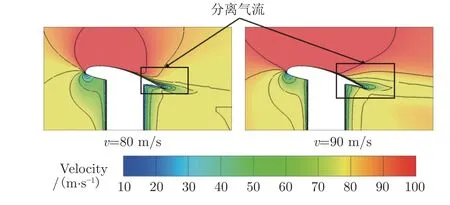
图12 升力翼气流分离点对比Fig.12 Comparison of lift wing air flow separation points

受风洞试验最大风速限制，通常无法模拟真实条件下的风速。本节研究表明，升力翼模型在v=90 m/s 以上时进入自模拟区，以弦长C 为特征长度计算的雷诺数约为3.1 × 106，可为风洞试验设计提供参考。

2.5 迎角对气动特性的影响

在有车–翼连接杆、H=3C、v=110 m/s 条件下，对不同迎角的升力翼进行数值仿真。图13（a）为迎角定义示意图，取翼型截面前缘A 点和尾缘B 点，定义A、B 两点之间连线和水平面的夹角为迎角α。图13（b）和（c）分别为不同迎角下的升力翼升力系数和阻力系数变化情况，升力系数和阻力系数采用式（6）计算。从图13 可以看出：随着迎角增大，升力系数先增大后减小，最大值出现在α=22°时，即该翼型在α=22°以上时出现失速。

图13 迎角对气动系数的影响Fig.13 Influence of attack angle on aerodynamic coefficient

3 结论

本文采用数值仿真方法研究了车–翼连接杆、来流速度、升力翼飞高及迎角对升力翼气动特性的影响，得到如下结论：

1）车–翼连接杆和升力翼的流场存在相互影响，但车–翼连接杆对升力翼的升力和阻力影响较小，分别在3.7%和3.4%以内。

2）在车顶前缘引起的高速气流影响下，在3 倍弦长飞高范围内，当升力翼飞高增大时，升力有减小的趋势。当迎角为12°时，升力翼在1 倍弦长飞高和3 倍弦长飞高的升力差在3%以内。

3）随着来流速度增大，升力翼升力系数先增大后减小，当来流速度达到90 m/s 以上时，升力系数稳定在1.62 左右；阻力系数不断增大，当来流速度达到90 m/s 以上时，阻力系数稳定在0.61 左右。

4）迎角在0°～22°时，升力翼升力系数随迎角增大而增大；迎角达到22°以上时，升力系数开始下降。