600km/h磁浮列车隧道交会车体压力载荷特征研究

魏康，来积伟，梅元贵

兰州交通大学 甘肃省轨道交通力学应用工程实验室，兰州 730070

0 引言

我国磁浮技术已经实现了从跟跑到领跑的历史跨越，高速磁浮列车弥补了铁路和航空领域之间的速度空白，但随着列车速度进一步提升，气动噪声、空气阻力和微气压波等问题日益严峻[1-3]。

磁浮系统和高速铁路系统的空气动力学经典研究方法和原理是相似的[4]。从1997年日本完成山梨试验线的建设开始，日本学者开展了多次实车试验，研究了空气动力学特性、舒适性、噪声和隧道内的气动载荷[5-9]。Saito 等[10]开发了一维流动模型来计算隧道中的压力变化和风速，并与日本旋成体动模型500 km/h 下的实验结果吻合良好。Huang 等[11]研究了列车明线交会时，列车的压力瞬态变化和滑流分布。梅元贵等[12-14]采用一维流动模型，研发了国内首套高速铁路隧道压力波源代码程序，构建了完整的数值仿真平台，并基于CFD 软件N–S 方程、SST k–ω湍流模型和动网格方法研究了高速磁浮列车初始压缩波特征。梅元贵与张志超等[15]还采用一维流动模型，研究了单列车通过隧道时，各种参数对车体压力载荷的影响。毕海权等[16]对磁浮列车的外流场进行了数值计算，得到列车风场特性。梁习锋等[17]采用动网格技术对不同环境风下的列车气动性能进行数值计算。焦齐柱等[18]结合压力舒适性标准，给出了磁浮列车最优隧道净空面积。关于磁浮列车的气动载荷，当前国内研究主要针对单列车通过隧道时车体和隧道壁面的气动载荷、缓冲结构对压力梯度的影响，以及声屏障压力载荷等[19-22]。而对于高速列车的气动载荷，目前研究主要关于多种工况下编组、线间距等列车及隧道参数对车体和隧道壁面的气动载荷影响等[23-29]。

《磁浮铁路技术标准（试行）》在隧道空气动力学方面，结合舒适性相关规定给出了600km/h下单、双线隧道的最小有效净空面积，但并未给出车体压力载荷建议值[30]。车体压力载荷反复作用会降低车体的使用寿命，严重时甚至会危害列车安全，磁浮列车交会工况下的车体压力载荷问题亟待解决。本文系统分析列车在交会工况下的车体压力载荷，研究成果可为列车的气动疲劳设计提供指导。

1 研究方法和验证

1.1 研究方法

一维可压缩非定常不等熵流动模型方法（简称一维流动模型方法）能够准确模拟任意工况下的隧道压力波及其他列车空气动力学相关问题。一维流动模型方法计算成本低，耗时短且经过多年发展完善，计算精度可满足工程应用。该方法对相关系数取值的准确度要求较高。

列车通过隧道时，引起的空气流动是三维可压缩非定常流动。当隧道长度远大于隧道断面水力直径，列车长度也远大于列车壁面与隧道壁面所形成环形空间横截面的当量水力直径时，可将三维流动合理简化为一维流动。本文研究的隧道为等截面且无竖井等辅助结构的零坡道简单结构隧道，考虑空气与隧道壁面和列车表面之间的摩擦和传热，假设隧道内空气为理想气体，一维可压缩非定常不等熵流动模型控制方程如下[12]：

连续性方程：

动量方程：

能量方程：

式中：p 为空气压力，u 为流速，ρ为密度，a 为声速，κ为比热容比，F 为空气流通截面面积，G 为摩擦项，q 为传热项，ξ为摩擦功，t 为时间，x 为流向坐标，具体参数含义以及求解过程详见文献[12]。

流动模型如图1 和2所示，其中vTR为列车速度。列车是长细比很大且在近地面高速运动的物体，在保证列车和隧道几何尺寸不变的基础上，用圆柱体代替列车和隧道，将模型简化为圆柱形列车在同心圆柱形隧道内运行。列车交会前、后过程与单列车通过隧道过程相似，但在交会过程中，同时存在单车环状空间和双车环状空间，流动模型更加复杂。

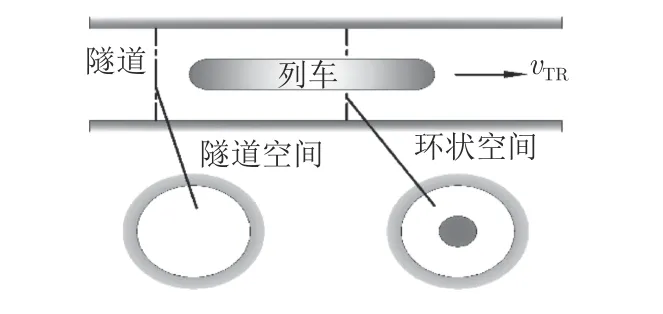
图1 单列车通过隧道时的空气流动空间Fig.1 The air flow space when a single train is passing through tunnel

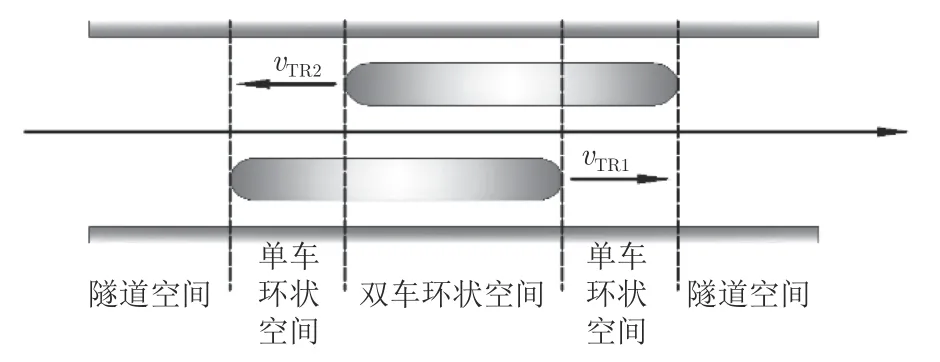
图2 列车交会时的空气流动空间Fig.2 The air flow space when trains are crossing in tunnel

1.2 验 证

利用中南大学高速磁浮列车动模型试验数据，验证本文一维流动模型方法在列车超高速运行[25]条件下的正确性和模拟结果的合理性及计算精度。

中南大学动模型试验隧道及列车参数如表1所示。图3 给出了一维流动模型数值计算结果与中南大学动模型（列车速度618 km/h）试验数据的对比，从图中可以看到数值计算结果与试验数据的压力曲线基本重合。试验数据负压值有一凸点，该点与数值计算结果相差20%，其余正、负压值误差分别在5%和12%范围内。由此可见，本文所使用的一维流动模型方法可以反映速度618 km/h 的动模型压力变化。

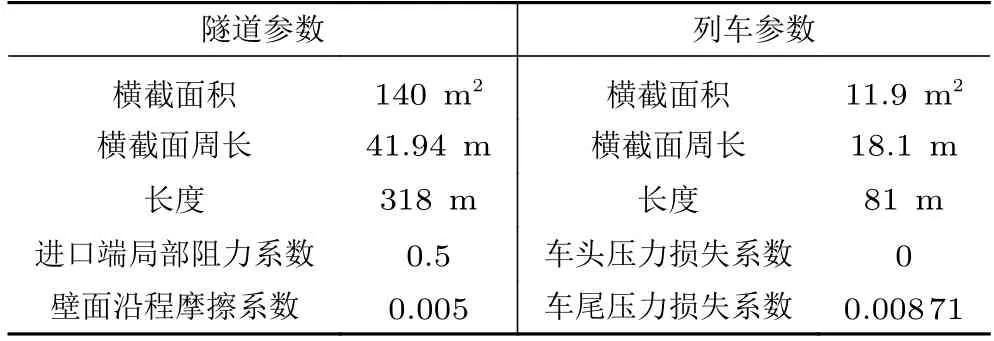
表1 中南大学磁浮隧道列车数据Table 1 Maglev tunnel data and train data of Central South University

图3 一维流动模型数值计算结果与动模型试验数据对比Fig.3 Comparison between numerical results of one-dimensional flow model and test data of moving model

2 计算结果分析

2.1 隧道内压力波的一维平面波特征

采用全尺寸磁浮列车模型，共5 节车厢，如图4所示[14]，磁浮列车采用T 形轨道梁，列车车高（H）4.20 m，车宽3.70 m，车体全长130 m，鼻长16.5 m。湍流流场的计算区域如图5所示，其中隧道长度LTU=500 m，车尾距计算域入口120 m，其余参数可参见文献[14]。数值计算采用CFD 计算软件，计算模型体网格如图6所示，其中体网格总数为4 243 万。湍流模拟采用N–S 方程和SST k–ω两方程模型。

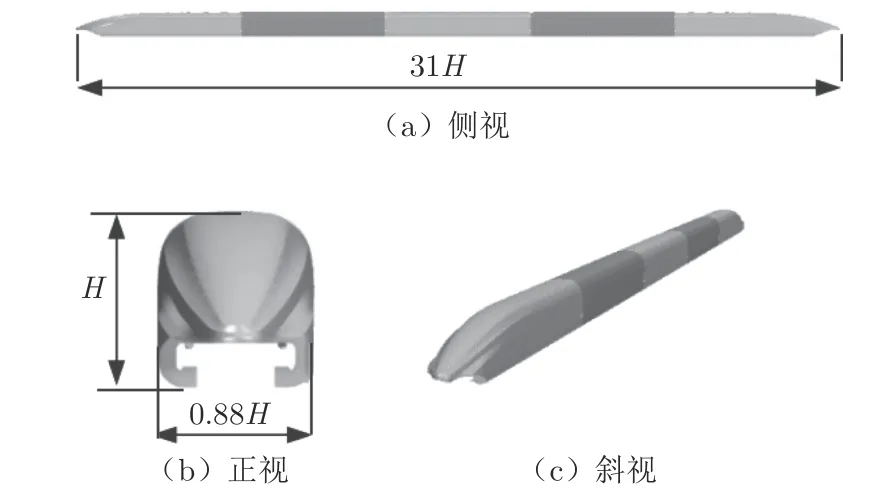
图4 高速磁浮列车几何模型示意图[14]Fig.4 Geometric models for high-speed maglev train[14]

图5 计算域模型[14]Fig.5 Model of computational region[14]

图6 计算模型体网格[14]Fig.6 Volume grids of computational mode[14]

文献[14]给出了磁浮列车在以600km/h的速度驶入隧道入口端的过程中，列车和隧道表面的压力变化特征，如图7所示。可以看到：当列车刚进入隧道时，隧道壁面两侧的压力分布不均，形成压缩波；随着头车继续驶入隧道，压力明显增大，车头前方压缩波向整个隧道内扩散，压力分布相对稳定。由此可知，由于隧道断面的非对称性，隧道入口附近压力呈现出三维特征，列车进入距离隧道端口一定距离后，呈现出显著的一维特征，从而验证了本文一维流动模型可以用来合理描述磁浮列车通过隧道时的气动载荷。

图7 一维平面波的演化过程[14]Fig.7 Evolution of one-dimensional plane waves[14]

2.2 车体压力波形成机理

图8 给出了速度600km/h的磁浮列车交会时，列车轨迹、压缩波传播过程和头尾车的压力时间历程曲线。图中A 为观测车，B 为通过车。以A 车为例，列车进入隧道，头、尾端诱发压缩波CAN和膨胀波EAT，传播至隧道出口反射后形成膨胀波EAN和压缩波CAT。列车驶出隧道出口时，同样也诱发压缩波和膨胀波向隧道内传播，但由于此时列车已经驶出隧道，因此对列车的车体压力载荷无影响。压缩波和膨胀波经过列车车体将会分别导致车体压力载荷的急剧升高和降低，特别是图8（b）中N–N（头头交会）和T–T（尾尾分离）时刻。两列磁浮列车交会过程中，头头交会时，车外观测点压力的急剧下降；尾尾分离时，车外观测点压力急剧升高。从整体上看，尾车压力变化规律与头车相似，但是压力变化整体会比车身进入隧道的时刻有所延迟。

2.3 车体最大正负压值特征分析

从图8（b）可以发现，车体压力几乎全部处于负压状态。为方便分析比较，引入定义：

图8 列车运行轨迹和压力时间历程曲线Fig.8 Schematic diagram of relationship between train trajectory and pressure time history curve

图9 和10 分别给出了隧道长度（列车速度为600 km/h）和列车速度（隧道长度为3 000 m）对车体最大正负压值的影响特性，研究发现：列车通过不同长度的隧道时，尾车的K 值先增大然后逐渐稳定在320 左右，头车的K 值先增大然后逐渐稳定在35 左右。列车以不同速度通过隧道时，头车的K 值变化范围为2～35，尾车的K 值变化范围为5～1 900，远大于头车。由此可见，列车在通过隧道的整个过程中，列车受负压值影响产生的车体膨胀远大于受正压值影响产生的车体压缩。

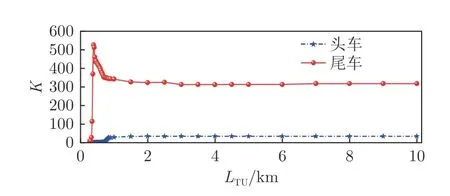
图9 列车通过不同长度隧道时的最大压力之比Fig.9 The ratio of the maximum pressure of a train passing through tunnels of different lengths

图10 列车以不同速度通过隧道时的最大压力之比Fig.10 The ratio of the maximum pressure of a train passing through a tunnel at different speeds

2.4 压力最值的分布特性

图11 给出了磁浮列车以不同速度（200、300、350、400、450、500、550 和600 km/h）通过不同长度隧道时，压力最值（最大正负压值和最大压力峰峰值）在车厢上的分布特性。从图11（a）可知：整体而言，当隧道长度超过1 km 时，最大正压值均出现在1 号车（头车）；当隧道长度小于1 km 时，列车速度为550 和600km/h时的最大正压值出现在2 号车，其余速度下出现在5 号车（尾车）。从图11（b）可知：整体而言，当隧道长度超过3 km 时，最大负压值均出现在5 号车（除400 km/h 外）；当隧道长度小于3 km 时，最大负压值基本都出现在1、4 和5 号车。当列车速度为400 km/h、隧道长度小于4.5 km 时，最大负压值出现在5 号车，反之出现在1 或2 号车。最大压力峰峰值大小由最大正负压值决定，图11（a）和（b）中最大正负压值基本出现在1 和5 号车，因此，最大压力峰峰值也都基本出现在1 和5 号车，极少出现在2、3 和4 号车（图11（c））。

图11 车体压力最值的分部特性Fig.11 The maximum pressure distribution

由此可见，压力最值的分布特性与列车速度和隧道长度密切相关，且呈一定的规律性，符合最不利隧道长度理论。值得注意的是，最不利隧道长度理论是基于头车最大正压值和尾车最大负压值的，但在隧道较短的情况下，最大正、负压值可能不会出现在头、尾车，而是出现在中间车，那么此时基于头车最大正压值和尾车最大负压值计算出的隧道长度则对应的不是车体压力最值。

2.5 隧道长度的影响特性

图12 和13 分别给出了磁浮列车以不同速度在不同长度的隧道中央等速交会时，隧道长度对车体压力载荷的影响特性。由图可知：整体而言，头尾车车体压力最值随速度的增大而增大；随隧道长度的增加先增大后减小，2 km 后基本保持定值；各个速度下，头尾车的最大正压值的定值基本重合，接近于“零”。最不利隧道长度的具体数值如表2所示。由表可知：当列车速度为600km/h时，最不利隧道长度小于400 m；头车最大正压值和尾车最大负压值对应的最不利隧道长度随着列车速度的增大而减小；头车最大负压值、尾车的最大正压值和头尾车最大压力峰峰值对应的最不利隧道长度随着列车速度的变化呈现出一定的波动。

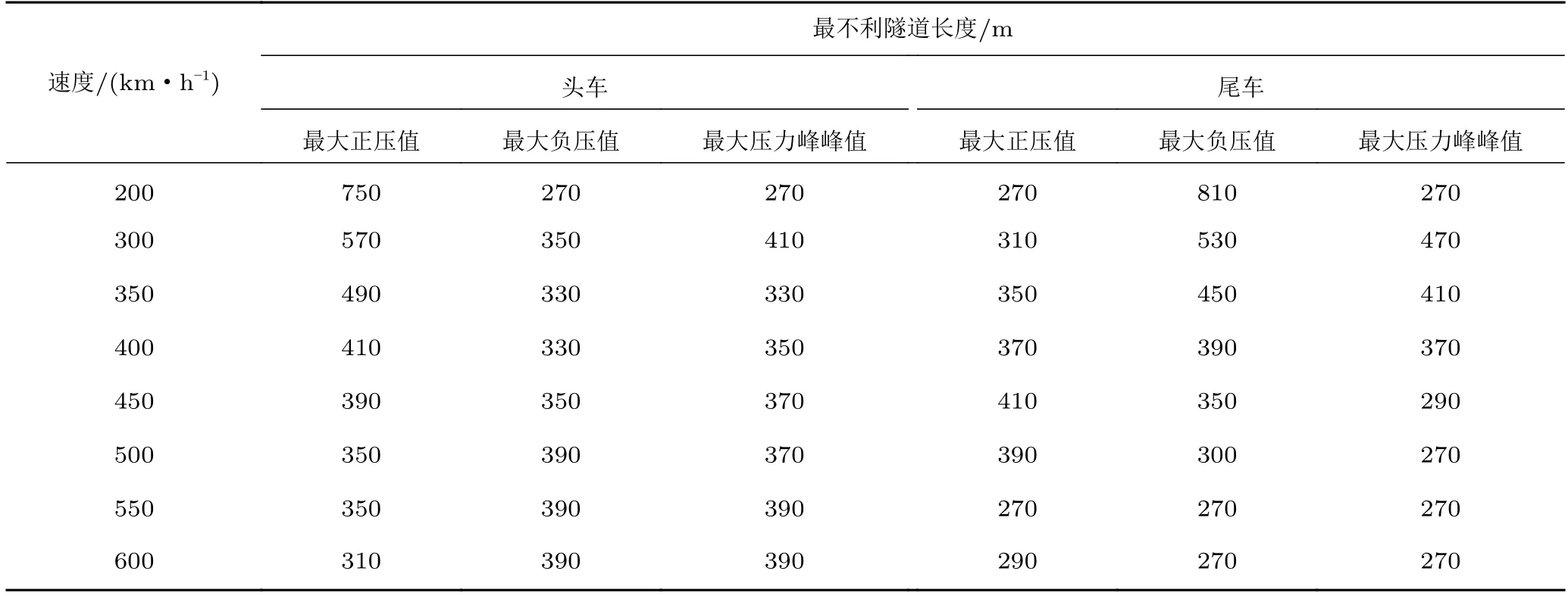
表2 最不利隧道长度统计表Table 2 Table of the most unfavorable tunnel lengths

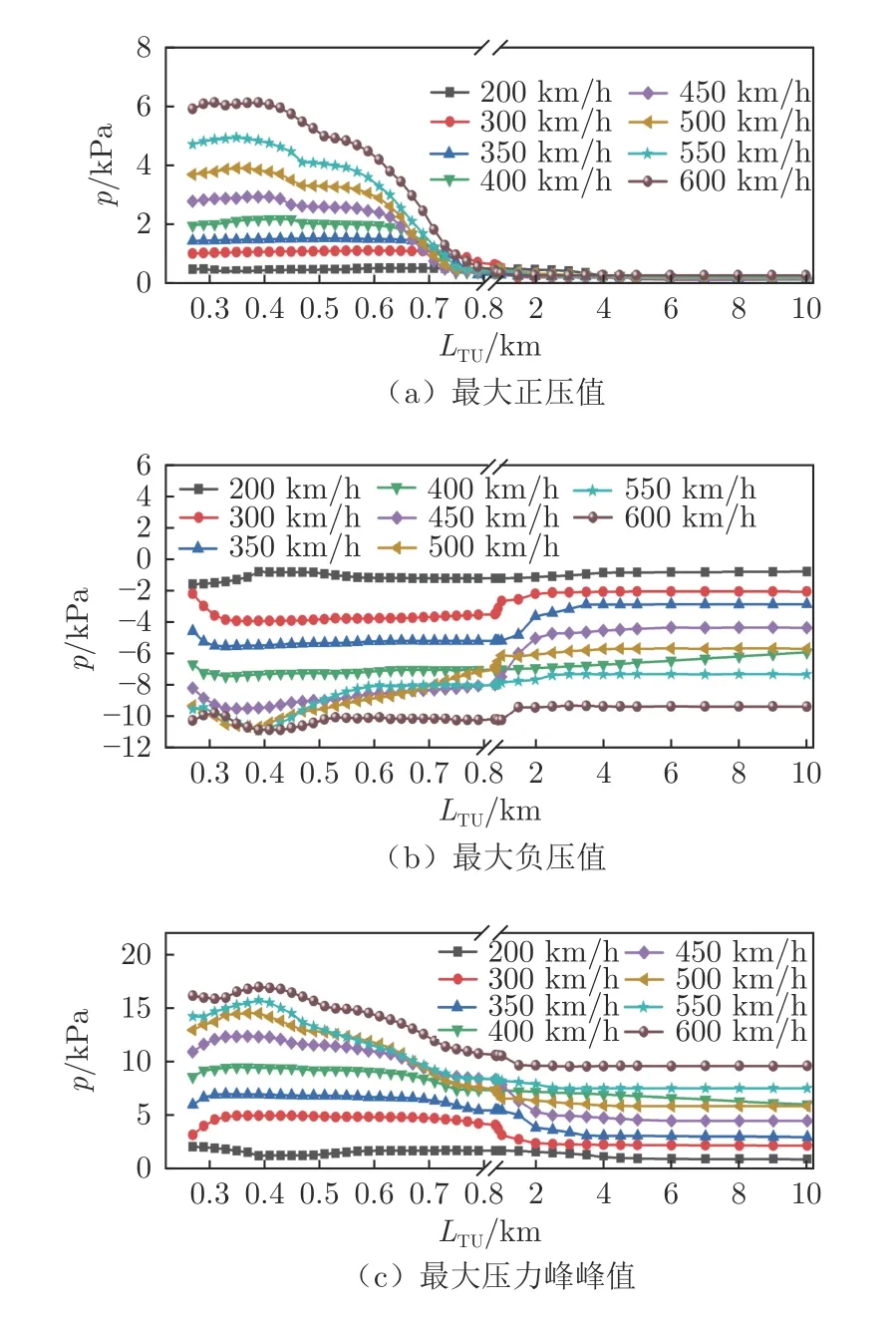
图12 头车车体压力随隧道长度变化Fig.12 The outside pressure of the head train varies with the length of the tunnel

图13 尾车车体压力随隧道长度变化Fig.13 The outside pressure of the tail train varies with the length of the tunnel

2.6 列车速度的影响特性

利用一维流动模型方法经济合理的优势，深入计算多种工况下列车在隧道内交会时速度对车体压力载荷的影响特性。

头尾车的最大正负压值与列车速度拟合曲线的幂次（n）关系如图14 和表3所示，表中R2为相关系数。随着速度的增大，列车车体压力最值也急剧增大。头尾车最大正负压值对应的n 值随隧道长度的增加而减小。当隧道长度为570～590 m 时，最大正压值与速度的二次方成正比；当隧道长度为350～370 m 时，头尾车最大负压值与速度的二次方成正比。随着隧道长度的增加，速度对车体压力载荷的影响逐渐减小。

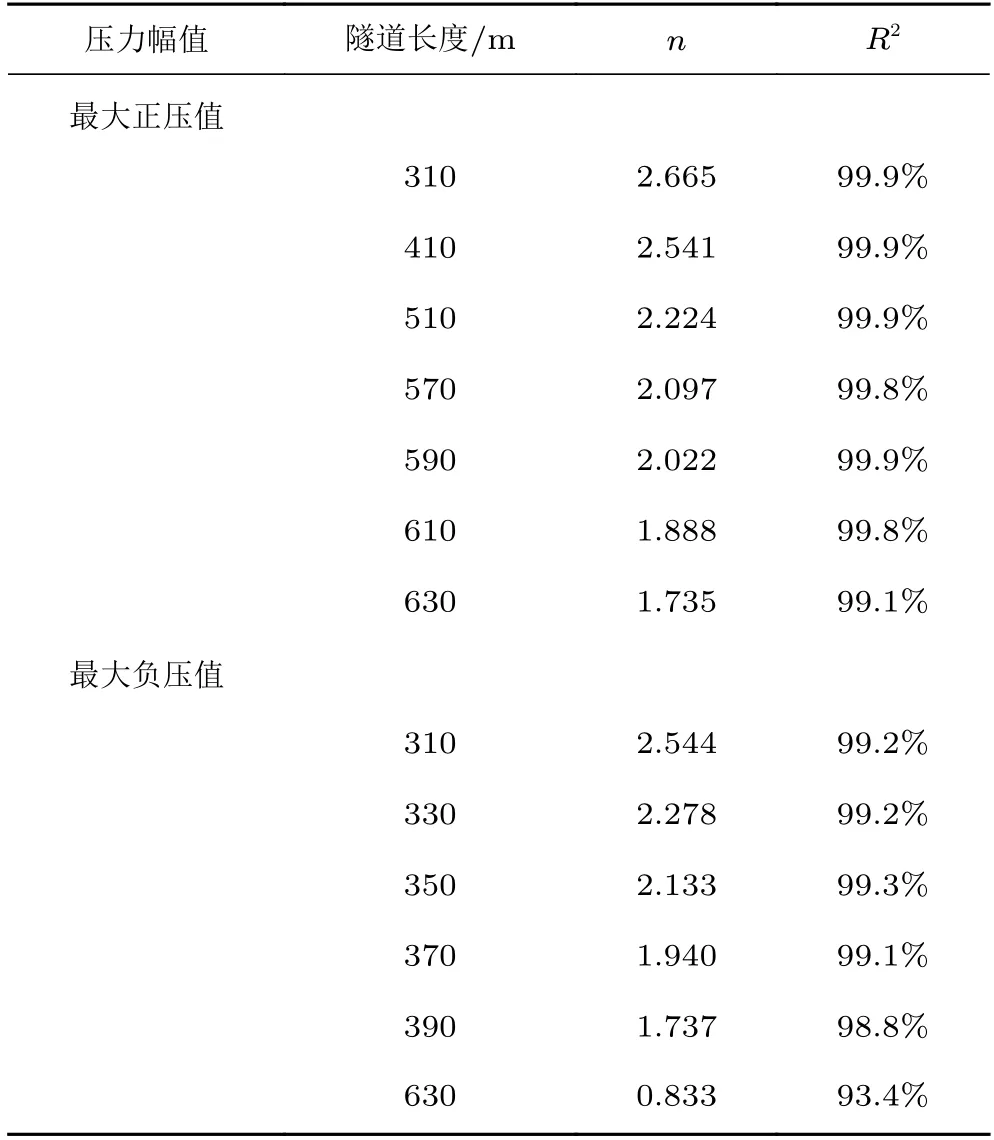
表3 不同隧道长度下头尾车压力最值与列车速度的幂次n 的取值Table 3 The value of the power n of the maximum pressure of head and tail train and train speed under different tunnel lengths

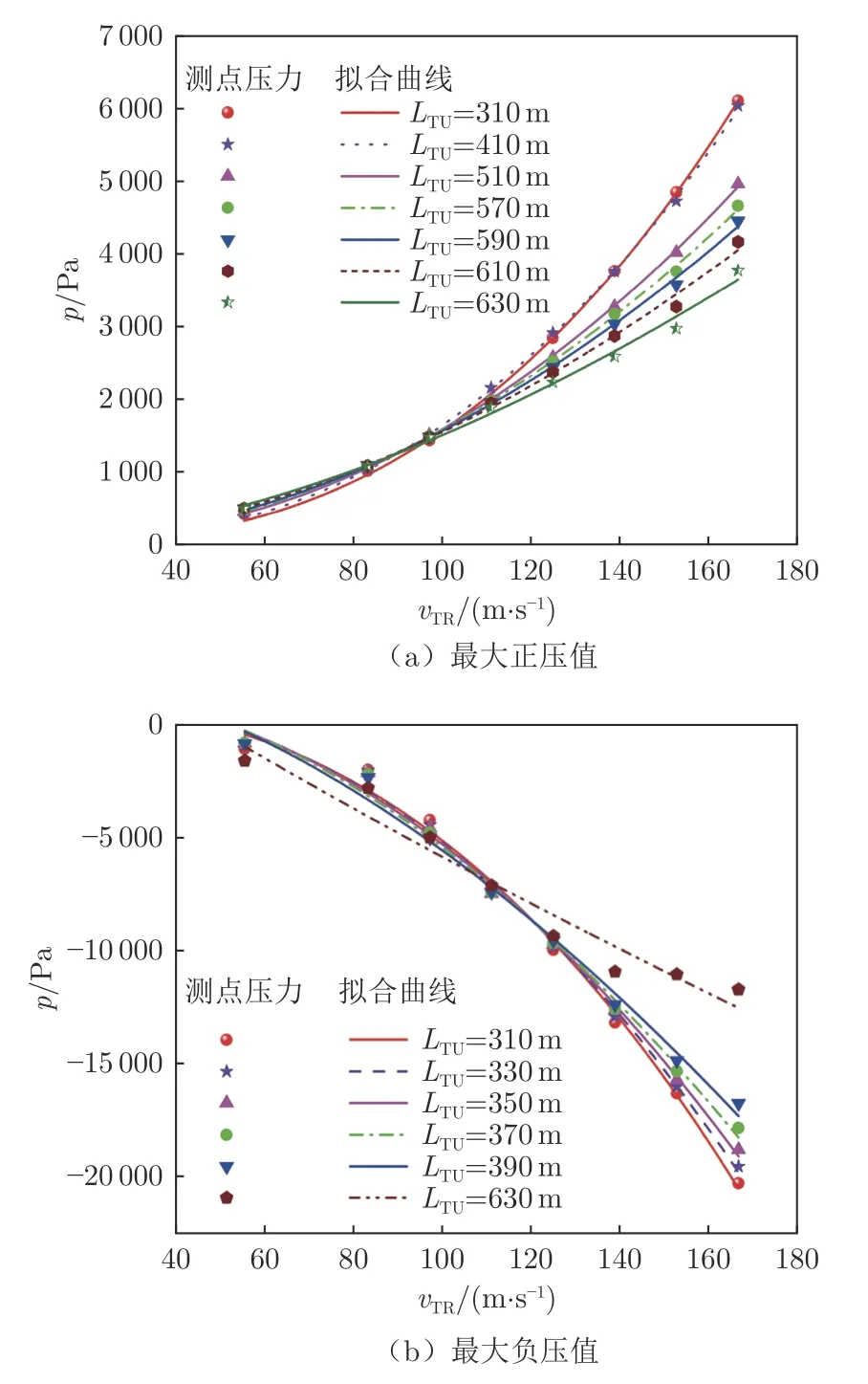
图14 头尾车车体压力最值与速度拟合曲线Fig.14 Fitting curves of maximum pressure and speed of the head and tail train

2.7 阻塞比的影响特性

根据2019年国家铁路局颁布的《磁浮铁路技术标准（试行）》，选取隧道净空面积为100、120 和140 m2，其对应的阻塞比分别为0.128、0.107 和0.091。图15 给出了头尾车压力最值随阻塞比的变化规律，由图可见，压力最值随阻塞比的增大而增大。表4 给出了头尾车压力最值与阻塞比拟合曲线的幂次（n）取值。可以看到，相关系数R2均在99%以上；头车n 的取值范围为1.14～1.23，尾车n 的取值范围为0.05～0.99。头车的最大正、负压值的增大速度大于尾车。

表4 头尾车压力最值与阻塞比的幂次n 取值Table 4 The value of the power n of maximum pressure of the head and tail train and blocking ratio

图15 头尾车的压力最值随阻塞比的变化规律Fig.15 The maximum pressure of the head and tail train varies with the blocking ratio

3 结论

本文在论证一维流动模型方法正确性的基础上，重点分析了600km/h磁浮列车隧道交会时，隧道长度、列车速度和阻塞比对车体压力载荷的影响特性，结论如下：

1）列车在通过隧道的过程中，车体基本处于负压状态。尾车的K 值波动较大，最大为1 900；头车的K 一般稳定在35 左右。

2）当隧道长度超过1 km 时，最大正压值出现在头车。当隧道长度超过3 km 时，最大负压值出现在尾车。压力最值分布与列车速度和隧道长度密切相关。头尾车的压力最值随着隧道长度的增加，先增大后减小，当隧道长度超过2 km 后保持定值。各列车速度下头尾车最大正压值的定值基本重合，接近于“零”。随着列车速度增大，头车最大正压值和尾车最大负压值对应的最不利隧道长度整体不断减小。

3）当隧道长度在一定范围内时，车体压力最值与速度的二次方成正比；车体压力最值随阻塞比的增大而增大，其中头车的最大正、负压值的增大速度大于尾车。