大气环境变化对真空管道温度场影响的研究

高超，严日华,*，武斌，周廷波

1.西北工业大学 翼型、叶栅空气动力学国家级重点实验室，西安 710072

2.中国空气动力研究与发展中心 设备设计与测试技术研究所，绵阳 621000

0 引言

随着中国高速、超高速轨道交通的快速发展，中国铁路轨道交通已然成为中国的新“名片”。为进一步推动中国铁路发展，国家铁路局在《“十四五”铁路发展规划》中提出“合理统筹安排400 km 级高速铁路关键技术、600 km 级高速磁悬浮系统技术储备等重大科技研发，突破关键技术”[1]。2022年10月20日，中国成功运行世界首个电磁撬设施[2]，吨级物体时速可达1 030 km，创造了大质量超高速电磁推进技术的世界最高速度记录，这一重大突破使得磁浮高速列车的进一步提速成为可能。但是，列车进一步提速将会带来十分严重的气动阻力[3-5]和气动噪声[6-7]问题。

近年来，一种将真空管道与磁悬浮列车相结合的新型设计方案引起了人们关注[8-12]。该方案能有效解决列车高速运行时的气动阻力和气动噪声问题，但低真空管道也带来了新的问题：列车在密闭真空管道内运行时，会产生较大的气动热，管道内温度迅速提升，容易造成悬浮电磁铁温度过高，导致电磁铁磁退，影响行车安全。围绕上述问题，研究者开展了广泛深入的研究。周鹏等[13-14]研究了真空管道超级列车高速运行时产生的激波结构及管道内的温度变化规律。包世杰等[15]研究了管道初始温度对超级列车气动阻力的影响。张俊博等[16]研究了真空管道磁浮列车表面温度随运行速度及真空度的变化规律。陈大伟等[17]研究了真空管道的管道横截面积、管道压力对磁浮列车气动特性的影响。魏龙涛等[18]研究了磁浮电磁铁温度随管道真空度及环境温度的变化规律。Zhou 等[19]采用两种不同阻塞比的管道列车模型研究了等熵极限和Kantrowitz 极限对真空管输送（Evacuated Tube Transportation,ETT）气动力行为的影响，并在不同速度下研究分析了列车头尾长度对减阻效果的影响规律。Yu 等[20-21]通过理论分析得到了管道壅塞影响因素及相关规律，采用数值计算方法研究了壅塞/非壅塞状态下的真空管道列车气动热特性和管道壅塞规律。胡啸等[22-25]基于SST k–ω模型和IDDES（Improved Delayed Detached Eddy Simulation）方法，采用重叠网格技术研究了列车车体热压载荷时均分布特征及波动特性，模拟了有轨道和无轨道时真空管输运的气动特性，揭示了非对称模型下的波系分布特征，讨论了轨道对流动和换热的影响；此外，还研究了不同车头长度的管道列车运行时的气动载荷和流场结构，得到了车头长度和列车运行阻力之间的规律。

以上研究主要讨论了真空度、阻塞比、管道内初始温度、列车运行速度等参数对列车运行时的阻力、噪声、激波以及气动热的影响。已有研究表明：管道内的温度分布与列车气动阻力和运行安全紧密相关。未来真空管道列车运输系统建设于露天环境之中，管壁及管道内部温度受到环境温度、风速、太阳辐射强度等诸多大气环境参数的影响，大气环境变化对真空管道气流温度分布的影响不能忽略。

本文基于四川省成都市近5年（2017—2021）的气象数据，建立真空管道辐射传热数值计算方法，采用DO 辐射传热模型对管道传热进行计算，分析太阳辐射强度、空气湿度、大气温度、平均风速等大气环境条件对真空管道内气流温度分布的影响，为未来真空管道列车运输系统建设提供参考。

1 数学模型分析

1.1 计算模型

本文主要研究太阳辐射对真空管道内气流温度分布的影响，故对真空管道进行简化，简化模型如图1所示。真空管道由直线电机定子、真空管壁和站台等组成。计算模型直径为6 m，长度为100 m，管道壁厚度为30 mm。

图1 真空管道模型示意图Fig.1 Schematic diagram of maglev flight tunnels

采用结构网格进行网格划分，计算域网格如图2所示。管道z 方向（坐标系如图2所示）上网格最大尺寸为200 mm，管道横截面网格最大尺寸为20 mm，网格总数为780 万。

图2 计算域网格图Fig.2 Grid diagram of calculation area

1.2 计算方法

真空管道并非意味着管道内绝对真空，而是处于一个较低的压力范围。随着管道内压力降低，管道内气体会逐渐出现稀薄效应。克努森数（Knudsen number）Kn[26]是判断该效应的主要依据：

式中：λ为分子平均自由程，L 为流动特征长度，T 为温度，p 为压力，d 为分子直径，kB为玻尔兹曼常数（1.380 6 × 10–23J/K）。当Kn 超过0.01 时，管内气流出现稀薄效应。列车运行的管道内压力为0.01～1.00 atm（约1.01～101.33 kPa），经计算，Kn 远小于0.01。因此，真空管道内的气体满足理想气体状态方程。

真空管道外部受到太阳辐射传热，管道内部热源之间也存在辐射传热，而管道流动区域为封闭区域。对于此类辐射传热问题，采用DO（Discrete Ordinate）辐射模型具有较好的收敛性。DO 模型适用于所有光学深度范围的辐射问题；既能求解无介质封闭区域问题，也能求解介质参与的辐射问题，适用于灰体、非灰体、漫反射、镜面反射及半透明介质辐射。

浮力基于Boussinesq 假设的三维Navier–Stokes方程为：

式中：u、v、w 分别为x、y、z 方向上的速度分量。

式中：ρ为空气密度，β为空气的体积膨胀系数，T0为参考温度，ν为运动黏性系数。

式中：α为空气热扩散系数，T 为流体温度。

1.3 计算工况

真空管道列车运输系统建设于大气环境中且尺度较大，因此需要考虑环境对管道内温度的影响。环境的温度、湿度以及风速都会影响管壁与环境的热量交换。

基于近5年（2017—2021）四川省成都市的气象数据（来源https://zh.weatherspark.com），得到了日辐射量、日照时间、温度、湿度和风速等影响真空管道运输系统传热的大气环境数据，绘制了成都市各月份的大气环境数据表，如表1所示。

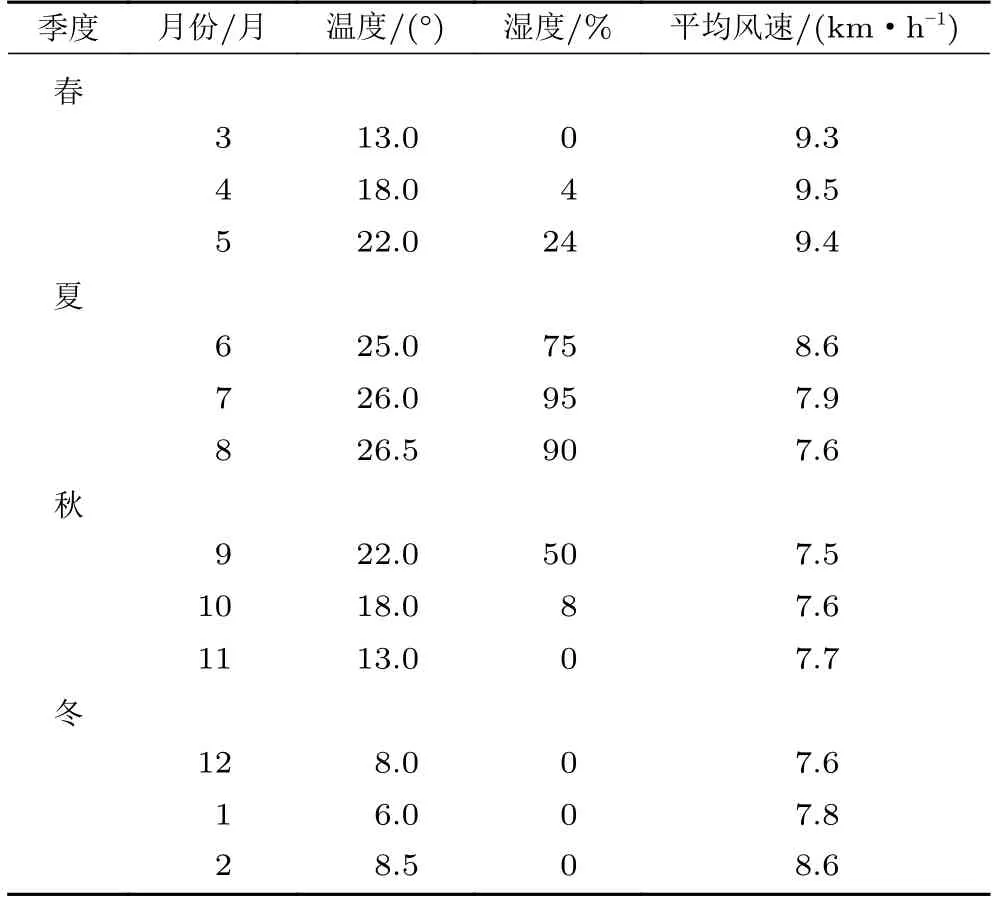
表1 成都市各月份气象数据表Table 1 The table of Chengdu monthly aerodynamic data

整理表1 数据，得到表2所示的成都市春夏秋冬四季的平均温度、平均湿度、平均风速等大气环境变量参数。

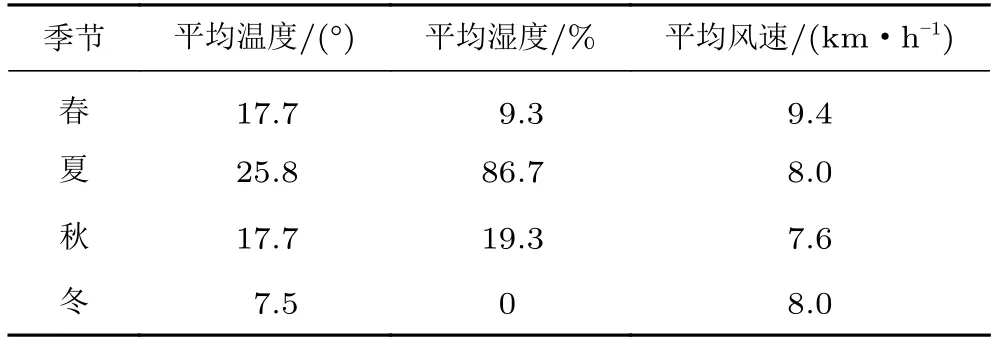
表2 成都市四季大气环境变量参数表Table 2 Table of meteorological data of Chengdu in different seasons

太阳辐射强度、照射角度随地理位置和时间变化。成都市中心地理坐标为（104.06° E,30.67° N）。辐射强度按照每个月晴天21 天计算，设置为各季度辐射强度最大值。辐射角度基于成都市各季度太阳辐射强度最大的月份北京时间13 时的平均太阳照射角度计算而得，并将计算结果作为边界条件输入至计算模型中。

各季度太阳辐射方向如下：春季（5月）辐射方向为（0.002 22,−0.982,−0.187），夏季（6月）辐射方向为（0.023,−0.991,−0.131），秋季（9月）辐射方向为（−0.012 5,−0.863,−0.505），冬季（2月）辐射方向为（0.075 6,−0.746,−0.661）。x、y 和z 方向与图2所示一致：z 轴正方向为真空管道列车运行方向，y 轴正方向垂直于地面指向上方。

1.4 壁面边界条件

真空管道材料为钢材，太阳辐射不能穿透钢材直接加热管道内部气流，只能通过辐射传热使得管壁外表面温度升高，以热传导方式将热量传至管壁内表面，进而影响管道内部气流流动。如图3所示，管道上壁面受到太阳辐射和自然对流的影响，下壁面为自然对流。在本文中，上壁面为受到太阳辐射的壁面，下壁面为太阳无法直射的壁面。在数值计算中，边界条件设置如下：上壁面为混合加热壁面边界条件，需设置换热系数、大气环境温度和辐射系数；下壁面为给定自然对流换热系数的自然对流壁面边界条件。由于管壁厚度与管道直径相比很小，此类壁面导热问题可以通过直接设置管壁厚度和壁面材料热导率进行求解。

图3 辐射传热和自然对流示意图Fig.3 Schematic diagram of radiation and natural convection

假设管壁为黑体，黑体辐射能力与热力学温度T 的关系由Stefan–Boltzman 定律确定：

式中，黑体辐射常数σ=5.67×10−8W·m−2·K−4，黑体辐射系数C0=5.67 W·m−2·K−4。实际物体的辐射能力E总是小于同温度下的黑体辐射能力Eb，两者比值即为实际物体发射率，记为ε：

因此，实际物体的辐射能力可以表示为：

综合考虑管壁受到太阳辐射以及管壁升温与外界环境产生的自然对流影响，真空管壁吸收的热通量可以表示为：

式中：Q 为管壁吸收的热量；hw为管道与环境大气之间的对流换热系数；Tamb为管道周围温度，Tg为管道壁面温度；天空温度（sky temperature）Ts可以根据Swinbank[27]表达式求得：

根据下式给出hw：

式中：kf为环境空气的热导率；Dh为特征长度，在本文算例中为管道直径；努赛特数Nu 可以表示为：

式中：Pr 为普朗特数；雷诺数Re 采用环境的平均风速求得；摩擦系数f 采用工程简化方式求得：

表3 为采用上述方法计算得到的各季节管道外壁面换热系数。将表3 中的系数和表2 中的平均温度作为壁面边界条件代入计算。管道外壁面换热系数hw仅与环境温度和太阳辐射强度有关，不随管道内气流参数而变化。

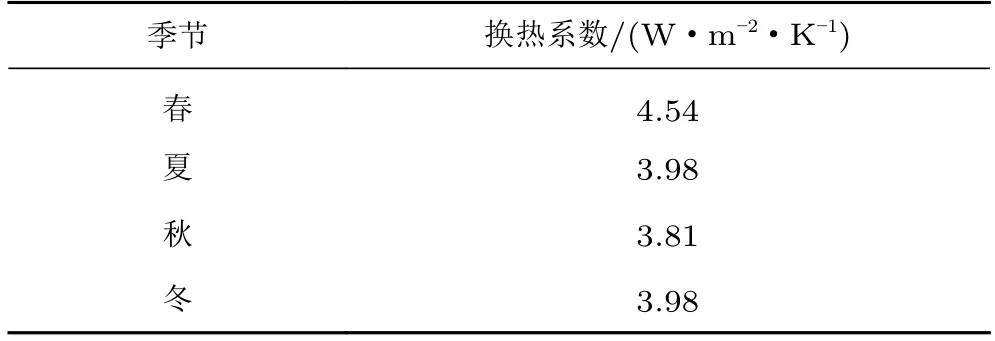
表3 各季节管道外壁面换热系数Table 3 Thermal convection coefficient of pipeline wall in different seasons

1.5 算法验证

真空管道传热属于管道流动和太阳辐射相结合的混合对流问题，该问题的计算模型和太阳能集热器（solar collector）一样。因此，将采用本文数值计算方法得到的结果与Polyakov[28]和Petukhov[29]得到的实验数据进行对比。实验的典型工况Case 1 和Case 2 如下（Gr 为格拉晓夫数）：

Case 1：Re=5.2 × 104,Gr=1.00 × 109

Case 2：Re=5.1 × 104,Gr=1.55 × 109

无量纲轴向速度W+、无量纲坐标D+和Gr 分别为：

式中：wa为管道流向中心截面圆心处的流向速度；R 为管道半径；x 和y 分别为管道横截面的横坐标和纵坐标，横截面圆心处x=0、y=0；q 为平均热流密度；k 为管道内部气流的热导率。

图4 为对比算例管道截面网格。采用结构化网格划分，划分策略与图2 相同，网格数量480 万。将管道中心截面处的横向和纵向无量纲速度分布与实验值进行对比，如图5所示。Case 1 的横向、纵向无量纲速度与文献中的实验数据基本一致。

图4 对比算例中的管道截面网格图Fig.4 Grid diagram at cross section

图5 Case 1 的数值计算和试验结果对比图Fig.5 Comparison of numerical calculation and test results in Case 1

图6 为Case 2 的横向和纵向无量纲速度分布对比图。可以看出，数值模拟得到的速度分布与实验数据具有较高的重合度，验证了所建立的管道内辐射传热和对流换热共同作用下的混合对流计算模型的准确性。

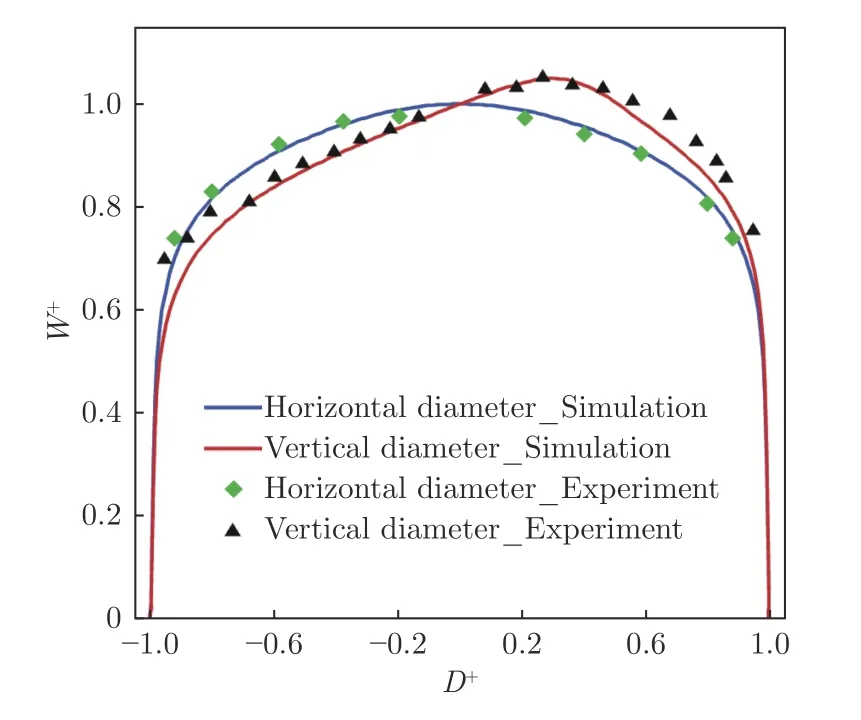
图6 Case 2 的数值计算和试验结果对比图Fig.6 Comparison of numerical calculation and test results in Case 2

采用所建立的辐射传热计算方法对真空管道进行辐射传热数值模拟。辐射传热计算收敛比较困难，计算时间较长，各算例在24 核高性能计算机上运行，计算时间约为36 h。

2 大气环境对真空管道的影响

2.1 真空度1.0 atm 时的管道内温度分布

采用建立的辐射传热计算方法对真空度1.0 atm（约101.3 kPa）的真空管道进行数值仿真。图7 为计算得到的管道中心截面（z=50 m）处的温度分布云图。从图中可以看出：管道上壁面受到太阳辐射的影响，温度提升较为明显；管道下壁面仅受到自然对流的影响，温度较低；管道内存在较大范围的温度分布均匀区域。管道内的气流温度基本沿截面垂向直径对称分布，这是由于本文使用的太阳辐射角度是基于成都市各季度太阳辐射强度最大的月份北京时间13 时的平均太阳照射角度计算而得，此时太阳位置基本位于管道正上方。在直线电机定子和管道下壁面附近存在一个温度较低区域，这是因为直线电机定子在列车运行时分段工作，本文暂未考虑直线电机定子发热的情况。

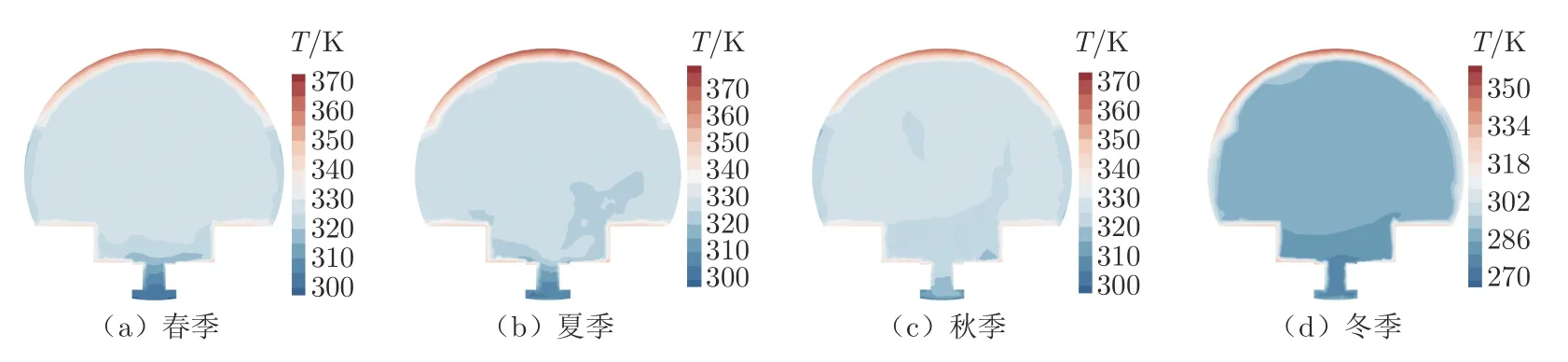
图7 真空度为1.0 atm 时各季节管道中心截面的温度分布Fig.7 Temperature distributions in different seasons when vacuum degree is 1.0 atm

图8 为管道中心截面（z=50 m）水平直径方向上的温度分布。从图中可以看出：x 方向上[−2.6,2.6]区域内的温度分布均匀，其中夏季管道内温度最高，春季次之，冬季管道内温度最低。这是由于夏季太阳辐射强度较大，外界环境温度较高，管壁与环境之间自然对流的热量较少，此时管道内稳定区域与外界环境的温差为30 K。冬季太阳辐射强度最低，环境温度最低，管壁与环境之间自然对流的热量较多，因此管道内温度与其他季节相比最低。冬季管道中心温度与外界温差为14 K。

图8 真空度为1.0 atm 时管道中心截面水平直径方向上的温度分布Fig.8 Temperature distributions along horizontal diameter of the middle plane of tube when vacuum degree is 1.0 atm

图9 为管道中心截面（z=50 m）竖直直径方向上的温度分布（y=−1.4 m 为简化模型中的站台位置）。可以看出：y 方向上[−1.4,2.6]区间内的温度基本稳定；管道上壁面附近存在一个较大的温度梯度区域，这是由于计算模型中按照北京时间13:00 计算太阳辐射角度，虽然各季节管道受到太阳辐射的区域不同，但均在管道顶部附近，故管道顶部（y=3.0 m 处）温度最高。在不同季节下，该温度最高的区域的大小几乎相同。

图9 真空度为1.0 atm 时管道中心截面竖直直径方向上的温度分布Fig.9 Temperature distributions along the vertical diameter of the middle plane of tube when vacuum degree is 1.0 atm

2.2 真空度0.5 atm 时的管道内温度分布

真空管道列车运行时，管道内并非绝对真空。本小节对真空度0.5 atm（约50.7 kPa）时的管道内温度分布进行计算。管道中心截面（z=50 m）的温度分布如图10所示。

在图10 中，真空度从1.0 atm 降至0.5 atm，管道内核心流域仍存在一个温度均匀分布区域；管道上壁面直接受太阳辐射影响，温度升高，热量传递至管道内，因此管道内存在一个较大的温度梯度区域；管道下壁面存在一个温度较低区域，这是因为此处未受太阳辐射影响，空气温升不明显。真空管道各季节受到太阳辐射的位置不同：春季（图10（a）），太阳从正上方照射管道；冬季（图10（d）），照射方向与y 轴则有明显夹角，导致管道壁面温度分布不同。

图10 真空度为0.5 atm 时各季节管道中心截面的温度分布Fig.10 Temperature distributions in different seasons when vacuum degree is 0.5 atm

图11 为管道中心截面（z=50 m）水平直径方向的温度分布。与真空度为1.0 atm 时相同，水平直径方向[−2.6,2.6]区域内也存在一个较为稳定的温度分布区域，此区域内仍是夏季温度最高，春季次之，冬季最低。值得注意的是：该区域春季温度略高于秋季，这是由于计算过程中的春季和秋季环境温度相同，而春季的太阳辐射强度略高于秋季。真空度为0.5 atm 时，管道内部各季节温度均有所提升，这是由于压强减小后，管道内气体密度降低，对流换热系数减小，导致管道内部散热量降低、温度提升。

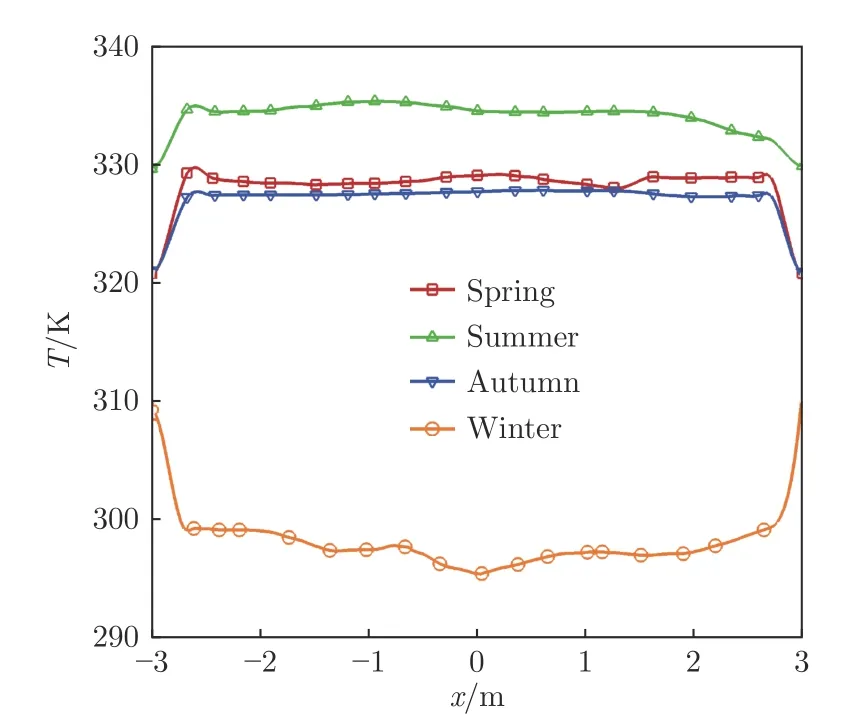
图11 真空度为0.5 atm 时管道中心截面水平直径方向上的温度分布Fig.11 Temperature distributions along horizontal diameter of the middle plane of tube when vacuum degree is 0.5 atm

真空度为0.5 atm 时，管道中心截面（z=50 m）竖直直径方向上的温度分布如图12所示。y 方向上依然存在一个温度分布均匀的区域。与真空度为1.0 atm 时相比，该区域内温度有少量的提升。值得注意的是，管道上壁面（y=3.0 m）和下壁面（y=−3.0 m）温度并未随真空度变化发生明显变化，这是由于管壁接受的太阳辐射传热量和与外界环境自然对流带走的热量均未变化，管道内部由气体重力和热浮力产生的空气对流速度很低，管道内壁面对流传热量与辐射传热量相比较低，因此管壁温度变化不明显。

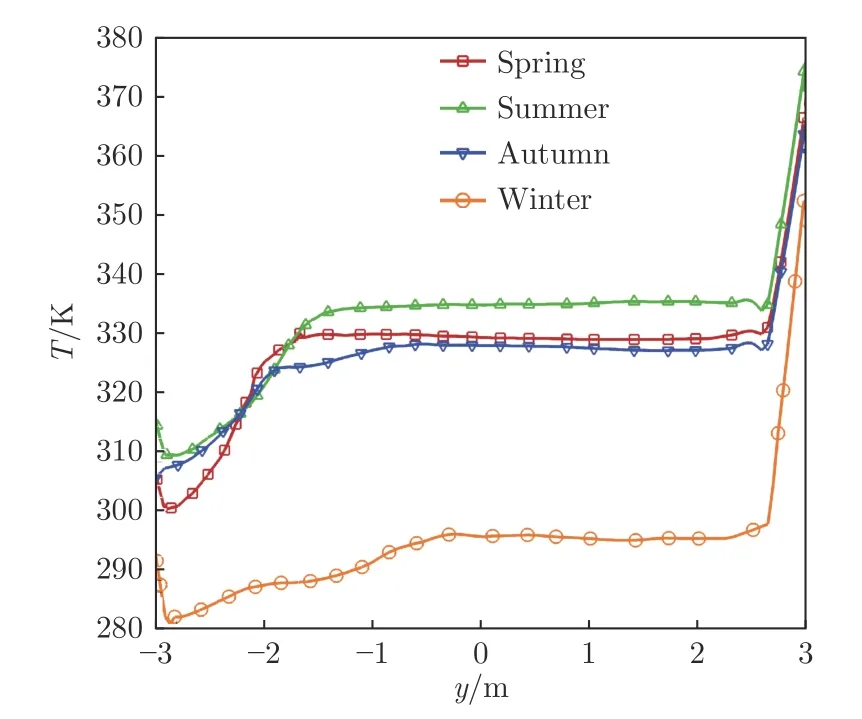
图12 真空度为0.5 atm 时管道中心截面竖直直径方向上的温度分布Fig.12 Temperature distributions along the vertical diameter of the middle plane of tube when vacuum degree is 0.5 atm

2.3 真空度0.1 atm 时的管道内温度分布

本小节对真空度为0.1 atm（约10.1 kPa）时的管道内温度分布进行分析。图13 为各季节管道中心截面（z=50 m）的温度分布。可以看出：管道中心截面处的温度分布规律与前文类似，在管道核心流域依然存在较大范围的温度均匀分布区域；春夏秋三季的温度明显高于冬季。

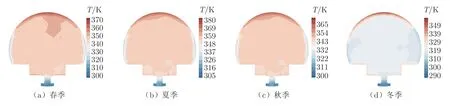
图13 真空度为0.1 atm 时各季节管道中心截面上的温度分布Fig.13 Temperature distributions in different seasons when vacuum degree is 0.1 atm

图14 为管道中心截面（z=50 m）水平直径方向上的温度分布。与前文不同真空度下相同的温度分布规律是：x 方向上[−2.6,2.6]区间内的温度基本稳定，夏季管道内温度最高，冬季管道内温度最低；真空度从1.0 atm 变化至0.5 atm 时，管内温度变化不明显，但气压降至0.1 atm 时，管道内温度分布发生明显变化，核心流域的温度明显升高。这是由于随着管道内真空度的升高，管道内气流的努塞尔数Nu 减小，对流换热系数减小，导致核心流域的温度明显升高。

图14 真空度为0.1 atm 时管道中心截面水平直径方向上的温度分布Fig.14 Temperature distributions along horizontal diameter of the middle plane of tube when vacuum degree is 0.1 atm

图15 为真空度0.1 atm 时的管道中心截面竖直直径方向上的温度分布。与真空度为1.0 和0.5 atm时相同，竖直方向上存在较大范围的温度稳定区域。但值得注意的是，管道内温度较之前工况提升明显：夏季，管道中心（x=0,y=0）的气流温度为355.60 K，比管道内的初始气流温度（299.00 K）提升了56.60 K；冬季，管道中心的气流温度为320.15 K，比环境温度（280.65 K）提升了39.50 K。

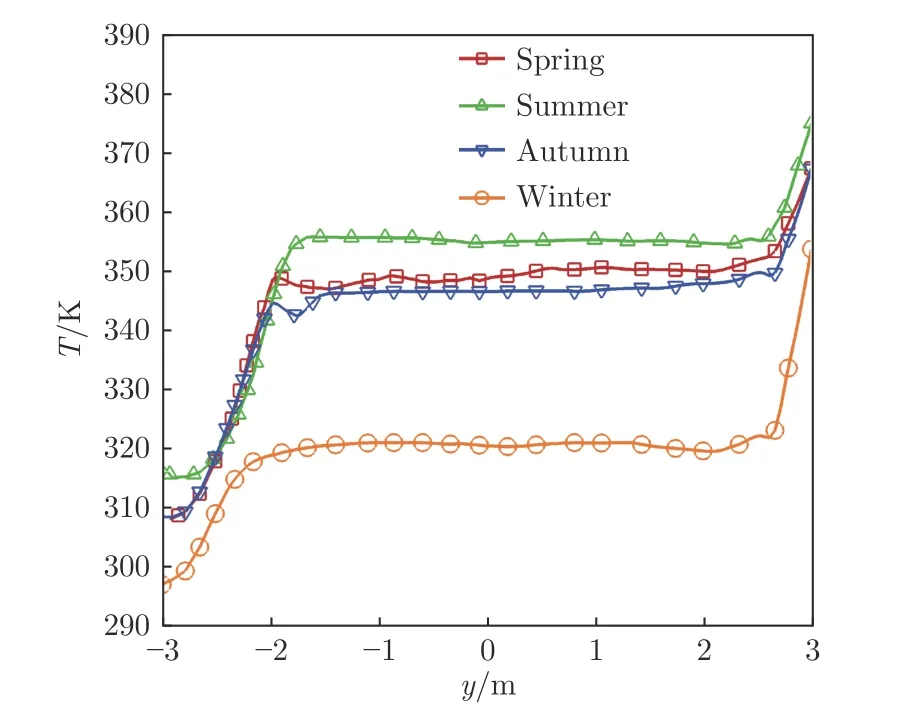
图15 真空度为0.1 atm 时管道中心截面竖直直径方向上的温度分布Fig.15 Temperature distributions along the vertical diameter of the middle plane of tube when vacuum degree is 0.1 atm

3 结论

1）当真空度发生变化时，管道内部始终存在一个较大范围的温度稳定区域；管道上壁面存在一个温度较高的区域，该区域内温度梯度较大；管道下壁面存在一个温度较低的区域。

2）各个季节管道内温度分布差异较大。夏季管道内温度最高，真空度为0.1 atm 时，管道内核心流域温度最高可提升56.60 K。冬季管道内温度最低，真空度为0.1 atm 时，管道内主流温度最高可提升39.50 K。

3）随着真空度降低，管道内气流换热系数减小，管道内温度逐渐升高。真空度从1.0 atm 变化至0.5 atm 时，管道内温度稳定区域内的温度稍有提升；真空度达到0.1 atm 时，管道内温度稳定区域的温度提升明显。

本文旨在研究大气环境对真空管道运输系统的影响，计算过程中暂未考虑真空管道列车运行时管道内的温度分布。在后续研究工作中，将进一步考虑列车运行时直线电机及电磁铁发热的辐射传热问题。