基于舒适性的高速磁浮铁路单线隧道最不利隧道长度分布特征研究

杜迎春，梅元贵

兰州交通大学 甘肃省轨道交通力学应用工程实验室，兰州 730070

0 引言

我国速度600km/h磁浮交通系统于2021年下线，目前正处于达速示范线路的规划研究阶段，这将对高速磁浮隧道空气动力学和相关验证研究提出更高要求。轮轨高速隧道压力波带来的乘客舒适性研究和相关运营经验[1-2]说明：更高速度的磁浮列车通过隧道时的乘客压力舒适性问题同样应该得到重视和解决[3]。

轨道交通乘客压力舒适性问题主要是列车通过隧道时诱发压力波传递至车内造成的，严重时甚至会导致乘客听力受损等情况[4]。轮轨高速的隧道压力波及舒适性问题已有较早且较全面的研究，这些研究对高速磁浮研究有重要的参考价值。轮轨高速相关研究[5-7]主要采用实车试验、缩尺动模型试验、数值模拟、压力舱试验等方法。其中，实车试验体现的列车空气动力学特征最为真实[8]，但试验结果取决于现有列车和隧道条件，而且受到环境条件的影响。王志钧等[9]采用实车试验研究了特定线路下350 km/h 动车组通过隧道时的车内外压力变化情况。缩尺动模型试验能够反映列车运行时的空气动力学特点，但完全实现几何相似、运动相似和动力相似较为困难。中国科学院力学研究所研制了缩尺比为1∶8 的高速列车动模型试验台并进行了验证[10]。三维流动模型数值模拟可对特定工况进行计算，并能够获得列车外形局部较为精细的流场结构和压力分布等，但计算数据量较大，计算成本较高[11]。一维流动模型特征线法计算快捷、成本低，可用于隧道净空面积、舒适性和车体气密性研究[5]。梅元贵等[12]采用一维流动模型特征线法研究了单列车通过不同长度隧道时车内压力变化特征，并提出了特长隧道条件下不同舒适性标准的适用性问题。一维流动模型数值模拟对于多工况、长隧道问题研究具有较强的适用性，磁浮列车相关问题同样可以采用该方法进行研究。对于轮轨高速舒适性的评价，标准中也涉及相关内容。UIC660[13]和《时速350 公里中国标准动车组暂行技术条件》[14]均采用车内每1、3、10 和60 s 内最大压力变化量不大于0.5、0.8、1.0 和2.0 kPa的限值条件评价乘客压力舒适性。

各国学者对高速磁浮隧道压力波及舒适性问题也展开了较多研究。德国学者Tielkes[3]指出磁浮列车通过隧道时应考虑压力舒适性、气动载荷和微气压波等“经典”空气动力学问题。日本学者山崎幹男等[15]使用实车试验和三维数值模拟方法研究了MX01 列车以500 km/h 的速度通过时隧道内的压力波动情况。国内梅元贵等[16]采用一维流动模型特征线法，研究了高速磁浮隧道的压力波特征。《磁浮铁路技术标准（试行）》规定了单车和交会时车内最大容许瞬变压力，其中单车采用每1、3、10 s 和任意时间车内最大压力变化量不大于0.3、0.8、1.0 和1.5 kPa 的限值条件来评价乘客压力舒适性[17]。

各国都有关于最不利隧道长度的相关规定，相关研究也是学者较为关心的问题。EN 14067-5 中规定了在研究车体气动载荷时所需要考虑的最不利隧道长度[18]。林洋等[19]基于隧道压力波传播和叠加理论，结合实车试验相关数据，分析了高速列车等速交会时的最不利隧道长度，但这并不适用于压力舒适性相关研究。马瑶[20]研究了动态气密指数为30 s、速度为350 km/h 的动车组考虑压力舒适性的最不利隧道长度。此研究对高速铁路隧道净空面积比选、多隧道线路上的压力舒适性分析和气密性设计等方面有指导作用，但缺乏不同列车参数对最不利隧道长度影响的研究，对高速磁浮相关研究的参考意义不明显。史宪明等[21]以每3 s 内的瞬变压力为基础，研究了低速磁浮双线隧道净空面积，初步得出了基于每3 s 内压力最大值的最不利长度隧道的特征，但并不适用于复合型舒适性标准。焦齐柱等[22]使用三维可压缩湍流模型研究了不同隧道净空面积、隧道长度和列车动态气密指数对单列磁浮列车通过隧道时车内压力的影响规律，提出满足舒适性标准的600km/h磁浮单线隧道最优净空面积，但研究者所使用的最不利隧道长度并非基于压力舒适性。张芯茹[23]研究了舒适性条件最不利隧道长度下高速磁浮隧道的净空面积，但对最不利隧道长度体系的构建甚少。在实际线路中，隧道长度不一、隧道密集程度不同，从而导致磁浮列车通过时的压力波动规律和舒适性不同。目前，在公开研究报道中，尚未见到关于舒适性问题最为严重的隧道长度和基于乘客压力舒适性的最不利隧道长度确定方法等较为系统的研究。

本文使用一维可压缩非定常不等熵流动模型的特征线法和时间常数法动态气密指数模型，研究单列车通过隧道时车内外压力波形成机理及不同隧道长度下车内外压力特点。通过分析单列车通过隧道时车外压力波及不同参数下车内压力变化特征，完善最不利隧道长度理论体系，得到不同列车速度和动态气密指数下最不利隧道长度分布特征及列车速度和动态气密指数对最不利隧道长度的影响规律。

1 研究方法和验证

1.1 数值模拟方法

空气具有可压缩性且隧道内流动空间受限，列车通过隧道时会在隧道内产生三维可压缩非定常湍流流动。考虑到隧道断面水力直径远小于隧道长度，列车与隧道壁面形成的环状空间当量水力直径也远小于列车长度。列车通过隧道时，列车鼻尖处压力具有明显的三维特征，但隧道压力波总体呈现一维特征[24]。本文采用一维可压缩非定常不等熵流动模型的特征线法计算磁浮列车车外压力，具体方法可参考文献[5]。

车内压力一般由车外压力确定，描述车内外压力关系的物理模型主要有时间常数模型、当量泄露面积模型和综合二者的优化模型[25]。车内压力计算采用以车内外压差趋于平衡的时间描述列车气密性能的时间常数模型[26]。假设列车为刚性，其计算公式为：

式中：pi为车内前后时刻的压差；po为车内外压差；t 为时间；τ为气密指数（分为静态和动态），单位为s。

1.2 验证

将数值模拟结果与中南大学动模型试验[27]的数据进行对比。动模型缩尺比为1∶20，换算为实际列车后，列车长度81 m、横截面积11.9 m2，换算为实际隧道后，隧道长度318 m、横截面积40 m2。图1为列车以618 km/h 的速度通过隧道时，距隧道入口端208 m 测点压力–时间历程曲线的数值模拟与中南大学动模型试验结果对比（∆p 为相对于大气压力的压差，即相对压力，后文压力均为相对压力）。图中蓝色圆圈处为列车头尾端驶过测点时的压力波动。在动模型试验中，列车速度随运行时间减小，这与数值模拟不同，则此处的压力变化也不同。除此之外，图1 中两条压力–时间历程曲线基本重合。动模型试验曲线负压值处有一凸点，该点处动模型试验与数值模拟数据相差20%，其余正、负压值处差异分别小于5%和12%，数值模拟结果可满足工程实际需求。

2 单线隧道车内外压力波特征

2.1 车外压力波特征

图2 为速度600 km/h、8 编组单列车通过长度5 km、净空面积100 m2的隧道时，列车头尾端压缩波、膨胀波及反射波的运行轨迹图和车厢外的压力–时间历程曲线，不同车厢测点位置均位于对应车厢表面垂直于列车长度方向的中间截面处。在图2（a）中，x 为距隧道入口端的距离，N 和T 分别表示列车头尾端轨迹线，CN和CNO分别表示列车头端进入和驶出隧道时产生的压缩波，ET和ETO分别表示列车尾端进入和驶出隧道时产生的膨胀波，EN1和CT1分别表示由CN和ET产生的反射波。图2（b）中水平虚线为对应车厢外压力的0 刻度线，竖虚线表示头尾车和中间车（第5 车）车外压力波形的时间历程特征，图中数值自上而下依次为第1～8 车的最大正压值（左）与最大负压值（右）。

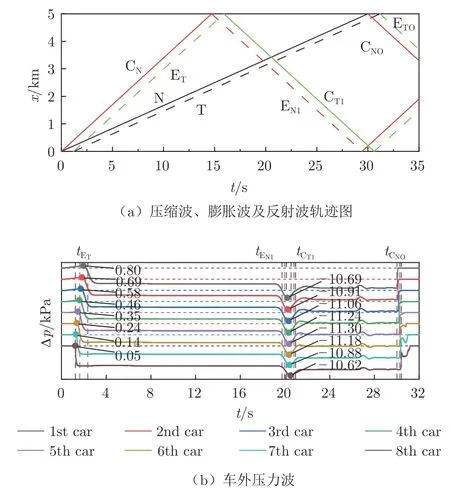
图2 高速磁浮单列车隧道压力波Fig.2 Tunnel pressure wave of high-speed maglev single train

列车在t0时刻进入隧道后，由于CN的作用压力开始上升，各车厢进入隧道的时刻不同，压力开始上升的时刻也不同。各车厢在tET时刻与ET相遇，车外压力下降，之后基本保持不变；尾端进入隧道的时刻与tET相近，这也使得尾车最大正压值最小。在tEN1时刻和tCT1时刻，不同车厢分别与EN1和CT1相遇，车外压力先降低后升高，产生最大负压值，第5 车该值最大，达−11.30 kPa。不同车厢在tCNO时刻与CNO相遇，压力上升；车头端驶出隧道的时刻和tCNO相近，所以头车外压力tCNO时刻变为0；在tCNO时刻之后，第2～5 车车外压力缓慢上升，第6～8 车车外压力先下降后上升。列车在t1时刻驶出隧道，车外压力恢复为0。

2.2 车内压力特征

图3 为图2 计算参数条件下的列车头尾车和中间车车内外压力–时间历程曲线，列车动态气密指数为3 和83 s，Δpex表示车外压力，Δpin表示车内压力[17]。对于列车而言，动态气密指数为3 s 说明车体气密性较差，此处选取该值，仅为了比较分析车内外压力。

从图3 可知，动态气密指数越小，车内外压差越大，车内压力的变化就越大。在动态气密指数为3 s条件下：t0t1时，车内压力逐渐上升。

图3 高速磁浮单列车内外压力对比Fig.3 Comparison of internal and external pressure of high-speed maglev single train

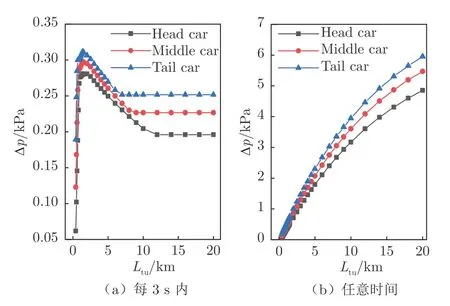
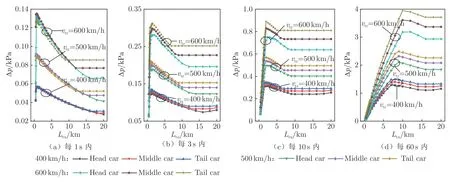
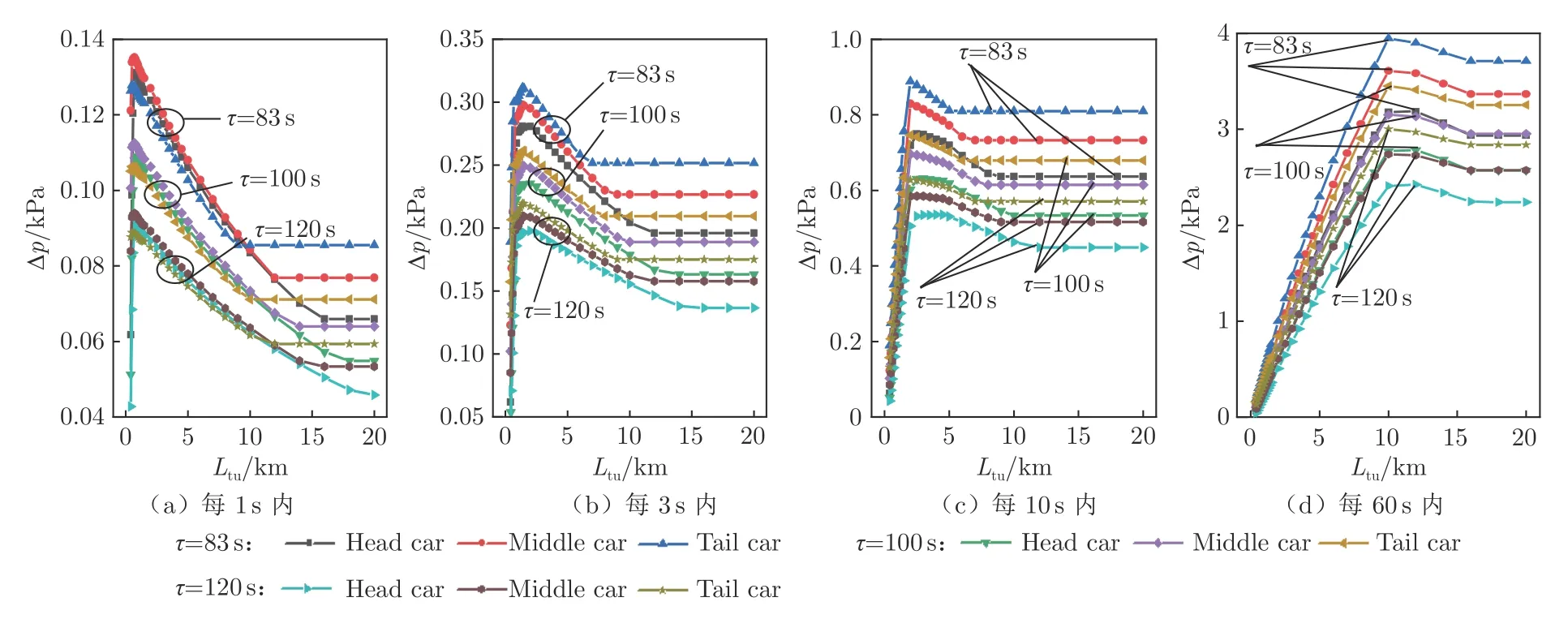
动态气密指数为83 s 时，列车密封性较高，车内压力变化主要有3 个阶段：t0t1时，车内压力上升，直至与车外压力相同。需要注意的是，当tCNO

图4 为动态气密指数83 s、速度600km/h的单列车通过0.596[28]、0.5、3 和10 km 的隧道时头车车内外压力–时间历程曲线，t'为时间与列车出隧道时刻比值的无量纲时间。0.596 km 是基于车头压力下降的最不利隧道长度，计算公式如式（2）。式中：Ltr为列车长度，Ma 为马赫数。该最不利隧道长度下的车外压力有最大负压值，随着隧道长度增大，车外压力负压值减小，但车内压力最大负压值增大。这主要是列车驶出隧道之前，较高的气密性使得车内压力始终大于车外压力，列车在隧道中运行的时间越长，车内压力最大负压值越大。这说明在上述最不利隧道长度下，车内压力并非最恶劣。

图4 不同隧道长度下高速磁浮单列车内外压力对比Fig.4 Comparison of internal and external pressure of high-speed maglev single train under different tunnel lengths

2.3 不同时间间隔最大压力变化量时间历程特征

综合UIC660[13]和《磁浮铁路技术标准（试行）》[17]中关于舒适性标准的约束指标，研究车内每1、3、10、60 s 和任意时间内最大压力变化量，分别以Δpmax,1s、Δpmax,3s、Δpmax,10s、Δpmax,60s和Δpmax,AT表示，Δpmax,AT的变化趋势可参考车内压力–时间历程曲线。图5 为在图2 计算参数条件下头车车内外压力和Δ pmax,1s、Δpmax,3s、Δpmax,10s、Δpmax,60s的时间历程曲线。其中，列车动态气密指数为83 s；t 时刻Δpmax,1s、Δ pmax,3s、Δpmax,10s、Δpmax,60s为t～（t + Δt）时间内车内压力最大值与最小值之差，Δt 为时间间隔。

图5 高速磁浮头车车内不同时间间隔最大压力变化量时间历程曲线Fig.5 Time course curve of maximum pressure variation at different time intervals in high speed maglev head car

隧道长度为5 km 时，Δpmax,1s与车外压力有着较为明显的对应关系，Δpmax,60s部分变化趋势与车内压力相近，Δpmax,1s、Δpmax,3s和Δpmax,10s最大值与车外压力最大负压值出现时刻接近，而Δpmax,60s最值出现在0～tET时刻。具体分析如下：

1）Δpmax,1s受短时间内车内压力变化的影响较大，而车内压力变化会受到车外压力瞬时变化的影响；Δpmax,60s受到列车通过隧道全过程车内压力变化趋势的影响。

2）当Δt >（t1−tET），即存在t 时刻使得t～（t +Δt）时间段内包含车内压力最大正压值和最大负压值，车内最大压力变化量最大值为车内压力最大正负压之差，如隧道长度为5 km 时Δpmax,60s的最大值。

3）当Δt <（t1−tET），则车内该时间间隔下最大压力变化量最大值出现在该时间段内车内外压差最大的部分。如隧道长度为5 km 时，Δpmax,1s、Δpmax,3s和Δpmax,10s最大值分别出现在19.77、19.49 和19.44 s，即19.77～20.77、19.49～22.49 和19.44～29.44 s 是车内外压差最大的时间段。

从上述研究可以看出：列车在不同长度隧道中运行的阶段不同，乘客的压力舒适性环境也不同。当列车驶出隧道的时间小于10 s 时，由于列车在隧道中运行时间较短，车内最大负压值较小，Δpmax,10s和Δpmax,60s最大值为车内最大正负压值之差，该值也较容易满足舒适性标准。这也说明列车速度一定时，隧道长度与乘客的压力舒适性密切相关。当然，对于乘客压力舒适性研究而言，主要考虑其最值是否满足舒适性标准限值，最不利隧道长度的研究同样仅考虑何种隧道长度下其最值最大，后续的研究主要考虑其最值的分布规律。

3 最不利隧道长度研究

3.1 计算参数

以8 编组某型磁浮列车为研究对象。列车长度（Ltr）为204.6 m，列车横截面积（Str）为12.80 m2。列车速度（vtr）分别为400、500 和600 km/h，列车动态气密指数（τ）分别为83、100 和120 s[17]。隧道长度（Ltu）范围为0.4～20 km，隧道净空面积（Stu）为100 m2。

3.2 基于舒适性概念的最不利隧道长度定义

从第2 节中可以看出，隧道长度既影响车内压力的变化，也影响不同时间间隔下车内最大压力变化量最大值出现的时刻和大小。图6 为隧道长度对头尾车和中间车Δpmax,3s和Δpmax,AT最大值的影响规律，其中列车速度为600 km/h、动态气密指数为83 s。由图6 可知：

图6 隧道长度对车内每3 s 和任意时间内最大压力变化量最大值的影响Fig.6 The influence of tunnel length on the maximum variation of the maximum pressure inside the vehicle every 3 s and any time

1）随着隧道长度的增大，车内每3 s 内最大压力变化量最大值呈先增大后减小的趋势。可见隧道存在某一长度使得Δpmax,3s最大值最大。在此隧道长度下，乘客所经历的车内压力就3 s 这一时间间隔内的舒适性标准而言是最恶劣的。在一定列车长度、速度和气密条件下，可将Δpmax,3s最大值随隧道长度先增大又减少的“拐点”所对应的隧道长度定义为每3 s 舒适性指标的最不利隧道长度。

2）对于任意时间而言，Δpmax,AT最大值随隧道长度增大而增大，不存在如Δpmax,3s的最大值随隧道长度增大而减小的“拐点”，所以不存在本文定义的基于舒适性指标的最不利隧道长度。

3）在针对轮轨高速的EN 14067-5[18]标准中，单列车最不利隧道长度LEN计算公式如下：

式中：c 为声速。

然而，式（2）和（3）在舒适性问题上并不适用。就压力变化量波动范围而言，最不利隧道长度应在压力变化量波动值相差较小的隧道长度范围内，可视为隧道长度的一种“集合”。本文确定最不利隧道长度“集合”的方法是：找出所计算的隧道长度下Δpmax,1s、Δpmax,3s、Δpmax,10s和Δpmax,60s最值的最大值，再研究与该压力值相差≤2%的隧道长度范围，就得出了最不利隧道长度集合。

3.3 列车速度对最不利隧道长度的影响

图7 为不同速度单列车通过隧道时隧道长度对头尾和中间车Δpmax,1s、Δpmax,3s、Δpmax,10s和Δpmax,60s最大值的影响特性，其中列车动态气密指数为83 s。表1 为不同速度下所确定的头尾车和中间车最不利隧道长度集合的交集，该交集代表头尾车和中间车压力舒适性均较差的部分，是更需要研究的隧道长度集合。

图7 列车速度对不同隧道长度下不同时间间隔车内最大压力变化量最大值的影响Fig.7 Influence of train speed on the maximum variation of the maximum pressure inside the vehicle at different time intervals under different tunnel lengths

表1 不同列车速度下最不利隧道长度分布Table 1 The critical tunnel length distribution under different speeds of train

由图7 和表1 可知：随着列车速度的增大，头尾车和中间车Δpmax,1s、Δpmax,3s、Δpmax,10s和Δpmax,60s最大值增大，且每3、10 和60 s 限值条件下的最不利隧道长度集合最小值均增大，最大值不变或增大，即最不利隧道长度集合的隧道长度边界值变化趋势为随列车速度增大而增大。动态气密指数为83 s、速度为600km/h的单列车通过净空面积为100 m2隧道时，每1、3、10 和60 s 限值条件的最不利隧道长度随时间间隔增大而增大。Δpmax,1s、Δpmax,3s和Δpmax,10s最大值均满足UIC660 的舒适性标准，每60 s 限值条件最不利隧道长度下乘客压力舒适性更需要被考虑。

3.4 动态气密指数对最不利隧道长度的影响

图8 为在不同动态气密指数（83、100 和120 s）下单列车以600km/h的速度通过隧道时，不同隧道长度对头尾车和中间车Δpmax,1s、Δpmax,3s、Δpmax,10s和Δpmax,60s最大值的影响特性。表2 为不同动态气密指数下的最不利隧道长度集合，其确定方法同表1。由图8 和表2 可知：随着动态气密指数增大，头尾车和中间车Δpmax,1s、Δpmax,3s、Δpmax,10s和Δpmax,60s最大值减小。相同动态气密指数下，对于不同车厢的Δpmax,1s、Δpmax,3s、Δpmax,10s和Δpmax,60s最大值而言，头车最小、尾车最大，且存在低气密指数下头车压力舒适性优于高气密指数下尾车压力舒适性的情况。从本文2.2 小节可以看出：尾车车内压力变化大于头车，较大的车内压力变化使得压力舒适性更为恶劣。不同动态气密指数（83、100 和120 s）下，除每10 s 限值条件下的最不利隧道长度外，所得出的最不利隧道长度集合基本不变。这主要是因为列车动态气密指数会影响车内Δpmax,1s、Δpmax,3s、Δpmax,10s和Δpmax,60s的大小，但对其变化规律以及最值的分布特征影响不大。不同动态气密指数下，每10 s 限值条件下最不利隧道长度变化规律的差异性可能是由隧道长度间隔选取较大导致的。

图8 动态气密指数对不同隧道长度下不同时间间隔车内最大压力变化量最大值的影响Fig.8 Influence of dynamic pressure tightness index on maximum pressure variation inside the train at different time intervals under different tunnel lengths

表2 不同动态气密指数下最不利隧道长度分布Table 2 The critical tunnel length distribution under different dynamic pressure tightness index

4 结论

在分析单列高速磁浮列车通过隧道时的车内外压力变化特征，以及隧道长度对舒适性指标影响规律的基础上，本文完善了基于压力舒适性标准的最不利隧道长度概念，并进行了列车速度和车体气密性对最不利隧道长度分布特征影响研究，可以为列车气密性和舒适性设计提供参考。具体结论如下：

1）基于车头压力下降的最不利隧道长度，头车车外压力有最大负压值，车内压力最大负压值较小，车内压力并非最恶劣的情况。

2）在基于列车气动载荷的最不利隧道长度和基于压力舒适性标准的最不利隧道长度均为所考虑条件下最恶劣的隧道长度，但后者是基于研究乘客压力舒适性相关问题提出来的，确定依据与前者不同，二者并不互相适用。

3）不同速度下的最不利隧道长度有所区别；动态气密指数分别为83、100 和120 s 时，除每10 s 限值条件下的最不利隧道长度外，其余条件下的最不利隧道长度近似。

4）不同时间间隔的最不利隧道长度不同，且时间间隔越大，最不利隧道长度越长。动态气密指数83 s、速度600km/h的单列磁浮列车通过净空面积为100 m2隧道时，基于UIC660 舒适性标准的每1、3、10 和60 s 复合型标准最不利隧道长度分布为10～12 km。