高速磁浮隧道扩大等截面斜切型缓冲结构减缓初始压缩波机理研究

马智豪，景雪蕾，杜迎春，梅元贵

兰州交通大学 甘肃省轨道交通力学应用工程实验室，兰州 730070

0 引言

隧道内的初始压缩波由高速磁浮列车突然驶入隧道产生。该初始压缩波传播至隧道出口后，一部分以膨胀波的形式返回隧道，一部分以微气压波的形式向隧道出口外辐射。当微气压波峰值过大时，在隧道出口处会产生爆破音，带来严重的噪声污染[1]。

围绕轮轨高速铁路隧道缓冲结构缓解微气压波问题，国内外学者在缓冲结构缓解初始压缩波压力梯度方面做了大量工作[2]。2019—2020年，Saito 等[3-4]基于声学理论和旋成体动模型试验方法，进行了缓冲结构开孔研究。2021年，Miyachi 等[5]通过旋成体动模型试验方法，研究了狭缝型和长宽型开孔缓冲结构对初始压缩波的影响。2018年，Heine 等[6]通过试验与理论结合，测量了开孔型缓冲结构各孔的流量并分析了其机理。2013年，Uystepruyst 等[7]利用CFD 对缓冲结构的型式、长度、缓冲结构截面积与隧道截面积之比进行了研究。2020年，Kim 等[8]结合鲨鱼仿生，利用动模型试验方法，设计了新型缓冲结构。2015年，Xiang 等[9]利用CFD 研究了斜切式洞口对初始压缩波的影响，总结了斜切角度影响初始压缩波的经验公式。2019年，Li 等[10]基于CFD软件，分析了扩大等截面型缓冲结构长度对压缩波的影响及其机理。2021年，王田天等[11]利用动模型试验和数值仿真方法，研究了扩大斜切式开孔型缓冲结构对微气压波的缓解作用。2021年，王维洲等[12]利用数值仿真方法，分析了列车速度400 km/h 条件下不同缓冲结构截面积与隧道截面积之比对初始压缩波的影响。

相比于轮轨列车，磁浮列车速度更高，其空气动力学方面的问题更加显著。2003年，山崎幹男等[13]以山梨线高速磁浮列车为研究对象，利用实车试验和数值仿真的方法，研究了隧道内的压力波动特征。2015年，本田敦等[14-15]利用缩尺动模型试验方法，确定了超高速磁浮缓冲结构参数。梅元贵等[16-17]研究了隧道入口初始压缩波的空间分布特征和传播特性，发现初始压缩波在传播过程中会由三维演化为一维，并分析了缓冲结构对初始压缩波的影响。2022年，张洁等[18-19]利用数值仿真的方法，研究了高速磁浮列车截面扩大型缓冲结构长度和空腔结构对隧道入口初始压缩波以及隧道出口微气压波的影响。

对于轮轨高速隧道初始压缩波的研究，Mashimo等[20]分析了列车车头不同位置产生的压缩波特性，揭示了初始压缩波的形成机理；Heine[6]、Xiang[9]和Li[10]等分析了缓冲结构缓解初始压缩波的机理。对于高速磁浮隧道初始压缩波的研究，目前主要集中在磁浮列车通过隧道时的初始压缩波特性和不同缓冲结构对初始压缩波缓解特性等方面。高速磁浮列车初始压缩波的压力梯度最大值形成机理及扩大等截面斜切型缓冲结构对压力梯度最大值的缓解机理的研究较少。本文基于三维非定常可压缩流动N–S方程和SST k–ω湍流模型，对国内某型600 km/h高速磁浮列车–缓冲结构–隧道的耦合系统进行数值仿真分析。

1 计算模型及方法验证

1.1 列车及隧道计算模型

图1 给出了磁浮列车气动模型、隧道轮廓和车头横截面沿鼻长方向的面积及其变化率（式（1））分布特征。3 编组磁浮列车由头车、中间车和尾车组成，车厢间采用风挡连接。设车高H=4.20 m 为特征尺寸，车体总长为19.28H，列车宽度为0.88H，列车鼻长为3.81H。以拟议的海南高速磁浮示范线初步设计资料为依据，论文采用平直单线隧道，隧道净空面积为100.25 m2，隧道水力当量直径为8.90 m。

式中：S′为列车横截面积变化率；S 为列车横截面积；n 为横截面距车头鼻尖距离。由图1（c）可见，从鼻尖到平直车身，流线型明显的部位在距鼻尖0～5 m范围内，在距鼻尖约2.7 m 处横截面积变化率最大。

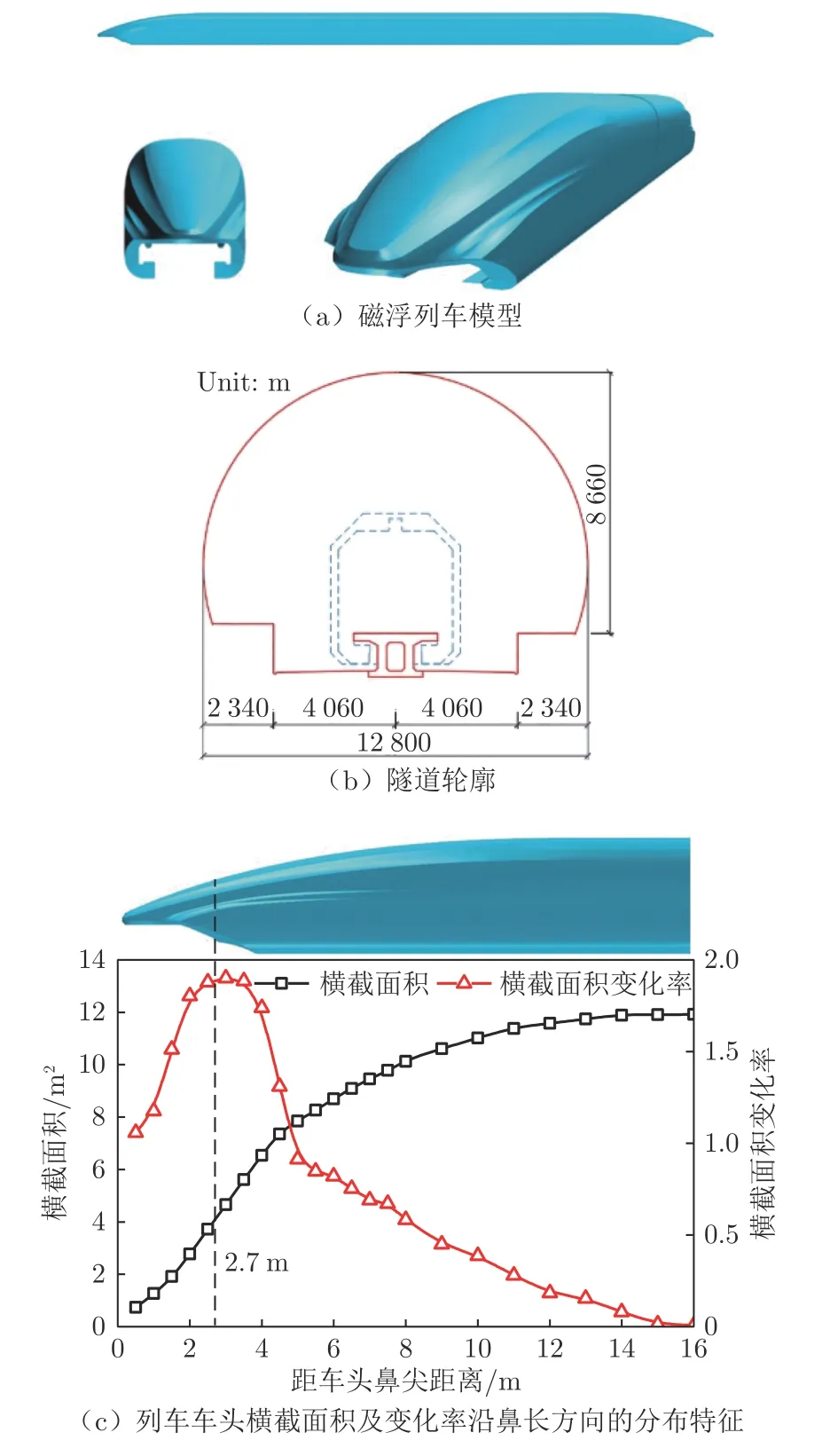
图1 列车和隧道模型以及车头横截面积变化Fig.1 The model of train and tunnel and the variation of cross section area of head

1.2 缓冲结构型式及参数

图2 给出了扩大等横截面斜切型缓冲结构和斜切端截面积及其变化率特征曲线。其中，在隧道的入口x=0（x 为列车运行的反方向）处，缓冲结构与隧道截面积之比为2.0，缓冲结构长度Lh=126 m，缓冲结构截面半径Rh=9.11 m，缓冲结构圆心与地面的距离h=4.31 m，θ为缓冲结构的斜切角度，Sh为缓冲结构横截面积，STU为隧道横截面积。本文研究的4 种斜切角度分别为10°、20°、30°和39°，斜切角度的选取参考缓冲结构斜切角度在轮轨列车方面的研究[9]。

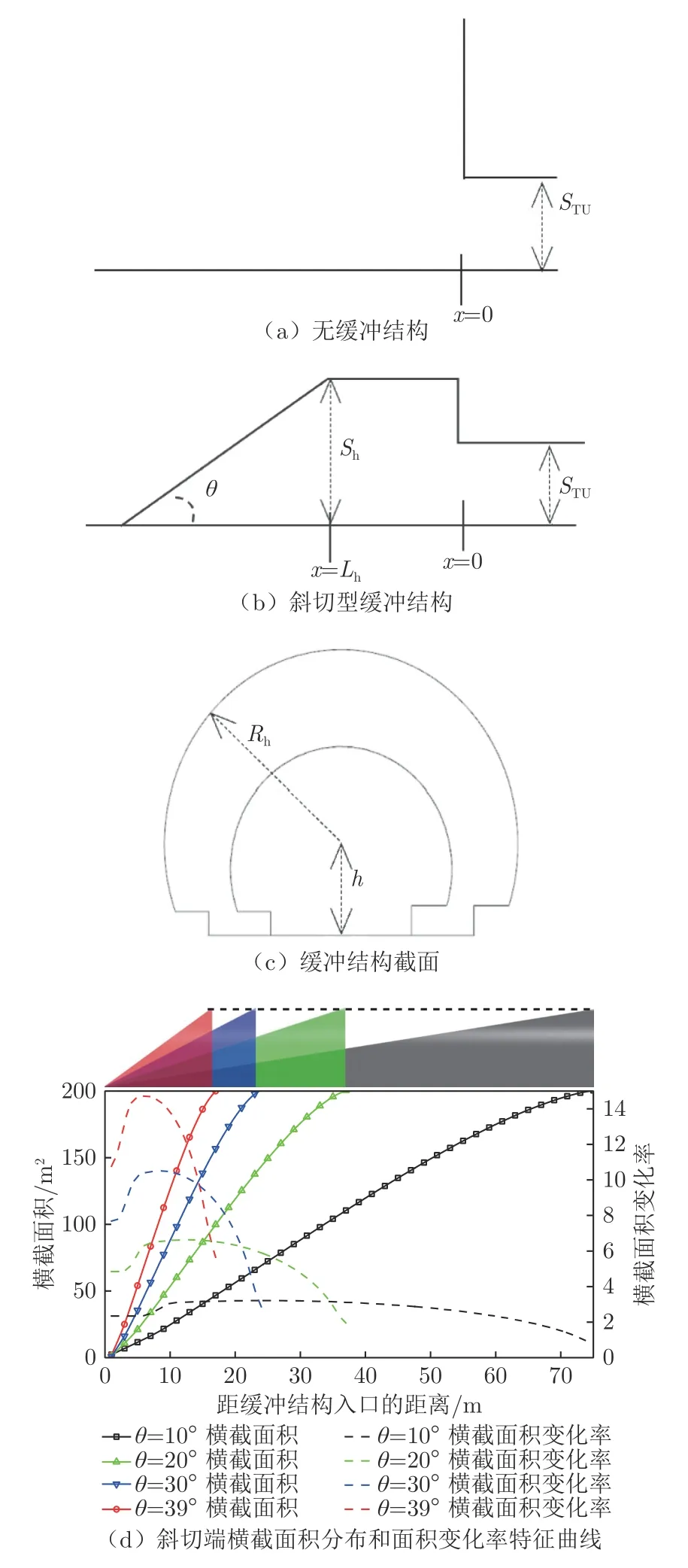
图2 扩大等横截面斜切型缓冲结构基本特征Fig.2 Basic characteristics of expanded equal cross section oblique hood

由图2（d）可知，缓冲结构斜切端截面积变化率随着θ的增大而增大。θ=20°、30°和39°对应的横截面积变化率峰值分别在距斜切端13、7 和5 m 处，θ=10°对应的横截面积变化率峰值在距斜切端10～38 m 处。

1.3 计算区域及边界条件

为实现列车在隧道中的运动，本文使用CFD 软件STAR–CCM+中的重叠网格技术。计算域分为靠近磁悬浮列车的重叠区域（移动区域）、包括隧道和地面的背景区域（静止区域）。

图3（a）和（b）为计算区域及边界条件示意图。隧道洞口前计算域长度为420 m，宽度为400 m，高度为200 m。车后空间长度为74 m[21]、光滑启动距离为210 m[22]、隧道长度为200 m[23]，列车距缓冲结构或隧道洞口55 m 时开始匀速行驶[21]。为获得充分发展的初始压缩波，在距隧道入口40、60、80 和100 m 处各设置一个测点截面，并在每个测点截面上布置5 个测点（图3（c））。

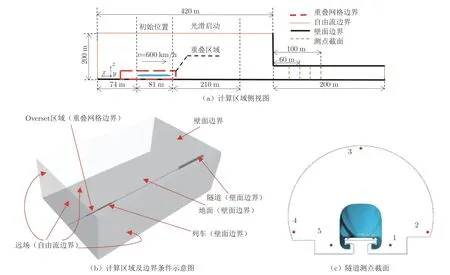
图3 计算区域边界条件及隧道测点布置示意图Fig.3 Computational domain and location of measurement points on tunnel surface

本文计算模型中的边界条件分别为无滑移壁面边界、自由流边界和重叠网格边界。自由流边界应用于计算域远场的上部和前后两端。重叠网格边界用于重叠区域的边界。列车、隧道、地面、缓冲结构及轨道表面采用无滑移壁面边界。计算模型的静态温度为288 K，静态压力为1 atm（101 325 Pa）。

1.4 网格划分

基于STAR–CCM+软件，采用结构化与非结构化结合的网格划分思路。外流场采用Trim 网格，固体壁面使用Prism 网格以便获取更精确的近壁面流场信息。取磁浮列车表面y+=40，近壁第一层网格厚度0.640 mm，拉伸8 层，拉伸比1.2；隧道壁面和缓冲结构表面y+（无量纲壁面距离）为50，第一层网格厚度0.899 mm，拉伸8 层，拉伸比1.5。图4 给出了磁浮列车的中等网格方案，车头网格尺寸为0.05 m，在车尾布置3 个加密块，为避免插值误差，本文网格尺寸从0.05 m 到0.40 m 逐渐变疏。图4中，红色和紫色网格分别代表overset 区域网格和背景区域网格。磁浮列车–隧道–缓冲结构耦合系统总网格数为2 300 万。粗糙网格和精细网格方案分别是减少和增加车头、车尾、磁浮列车滑橇及轨道间隙处网格尺寸，总网格数分别为1 300 万和3 400 万。

图4 磁浮列车的中等网格方案Fig.4 Medium grid scheme of maglev train

1.5 网格独立性研究

考虑计算精度和时间，本文进行网格独立性研究。在不同网格精度下，将4 个测点截面中测点3 的压力Δp 和压力梯度（dp/dt）进行对比，如图5所示（t=0 s 为磁浮列车鼻尖到达隧道入口时刻）。可以看到，在粗糙、中等和精细网格3 种情况下，压力上升曲线吻合良好；距隧道入口40、60、80 和100 m 处测点截面的测点压力梯度最大值的最大偏差分别为0.75%、0.72%、0.75%和0.74%。由此可见，本文采取的中等网格方案可行。

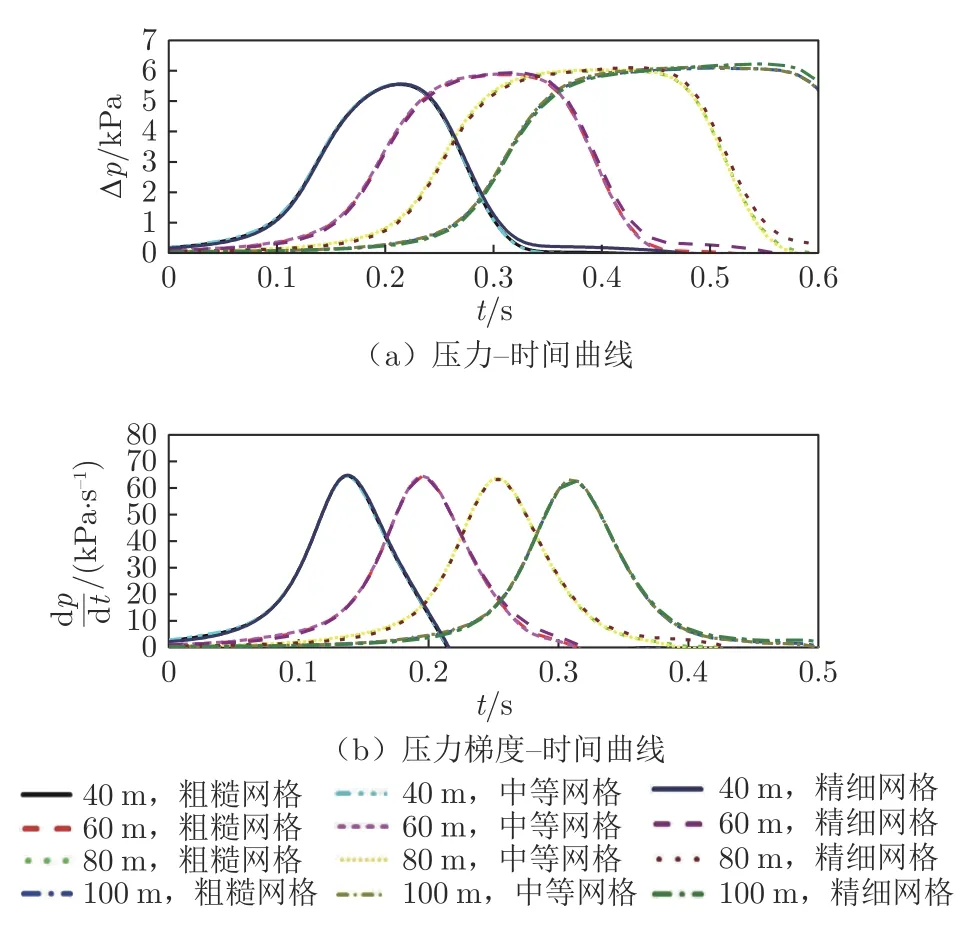
图5 不同网格精度下测点3 的压力和压力梯度对比Fig.5 Comparison of pressure and pressure gradient at measuring point 3 with different mesh precisions

1.6 计算方法验证

为验证本文数值方法和网格划分的正确性，将数值仿真结果与中南大学车速618 km/h、缩尺比1 ∶ 20 的磁浮动模型[24]单线隧道试验数据进行对比，该试验数据由中南大学列车空气动力学研究团队提供。缩尺后的隧道长度为40 m，净空面积为2.19 m2，列车为3 编组，压力测点P0在距隧道入口端25.88 m 处。

图6（a）为验证模型的网格展示。为验证模型的网格划分策略，采用SSTk −ω湍流模型，时间步为0.001 2 s，时间离散格式为一阶。图6（b）给出了测点P0处的静压随时间变化曲线。可以看到，极点1、2 和3 处数值仿真结果与试验数据的误差分别为10.13%、3.66%和3.05%，波形特征吻合度较高。数值模拟曲线在t=0.034 s 前与动模型试验曲线吻合较好，后者出现一定的延迟。其主要原因是动模型试验装置弹射的模型列车在没有动力的轨道上运行时，由于空气阻力和轮轨摩擦，速度略有下降，但这对压力大小和整体趋势影响不大[25]。进行磁浮列车动模型试验时，外界环境干扰不易控制，数值模拟和动模型试验的压力幅值存在一定偏差，但最大误差值仅约为10%，证实了本文数值方法和网格划分的正确性。

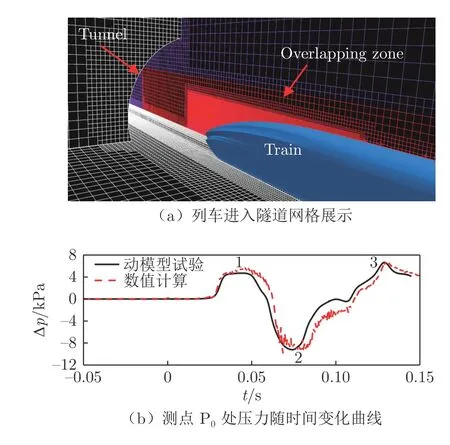
图6 验证模型网格展示和验证结果对比Fig.6 Display of validation model grid and comparison of validation results

2 计算结果和分析

2.1 无缓冲结构时初始压缩波的基本特性

图7 给出了磁浮列车车头进入隧道时，隧道壁面和地面轨道的压力分布和变化特征。其中，t=−0.048 s 为列车在隧道外距隧道入口半个鼻长的时刻；t=0.048 和0.096 s 分别为列车车头驶入隧道内半个和一个鼻长的时刻。由图可知：t=−0.048 s 时，列车未驶入隧道，隧道内压力已经开始变化并且已有微弱压力波向隧道内传播；t=0 s 时，隧道内列车车头附近的压缩波呈现三维特性，远离列车车头的压缩波已经呈现一维平面波特性，初始压缩波正在形成；t=0.048 s 时，初始压缩波正在向前传播，压力梯度上升；t=0.096 s 时，隧道内一维波不断向前传播，隧道内初始压缩波已经形成，且压力梯度已达到最大值。

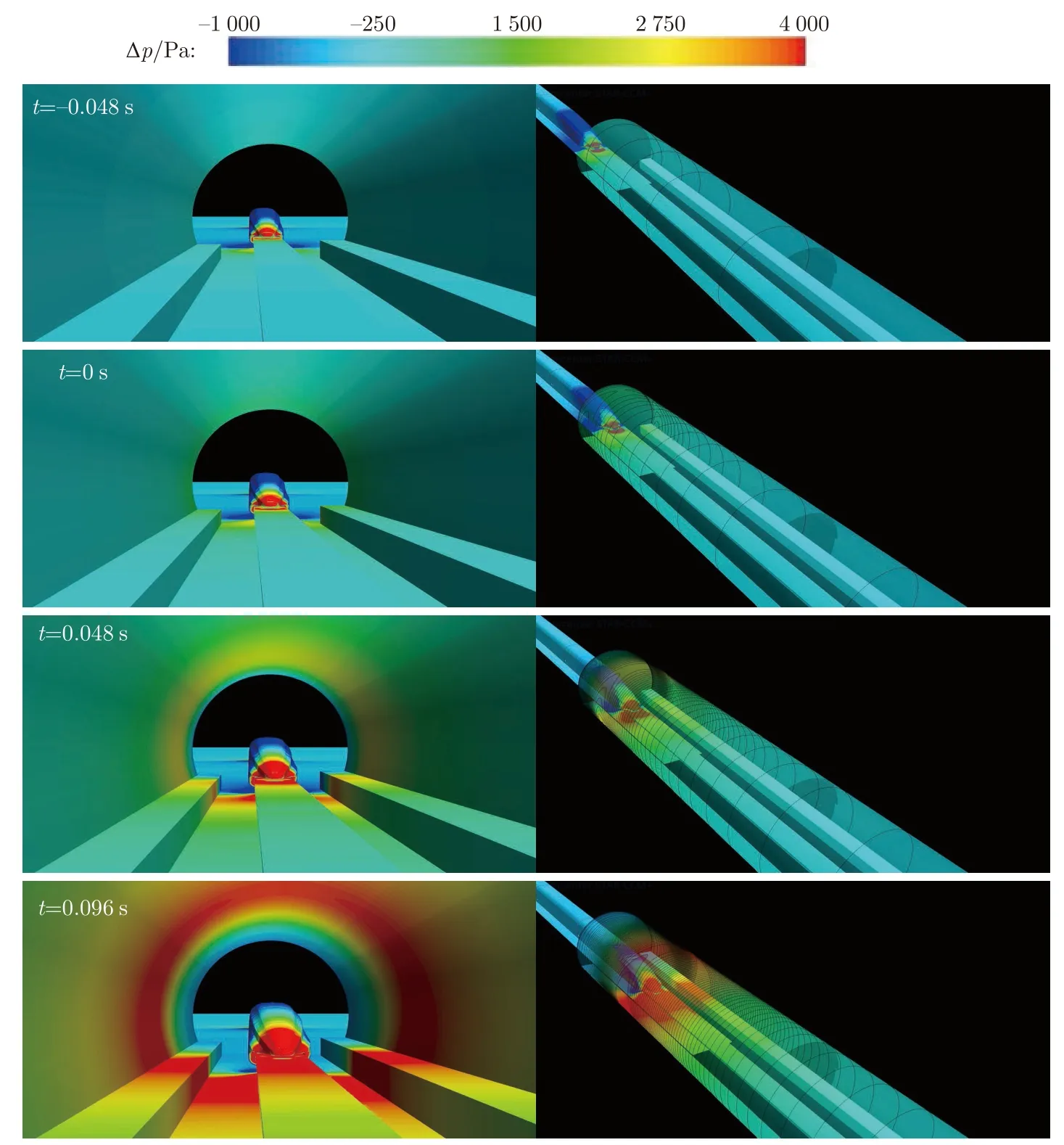
图7 隧道壁面和地面轨道的压力分布和变化特征Fig.7 Pressure distribution and variation characteristics of tunnel wall and ground track

以隧道内4 个测点截面中（分别距隧道入口40、60、80 和100 m）测点 3 的压力和压力梯度为研究对象，分析初始压缩波压力梯度变化的原因，如图8所示。可以看到，在不同截面上该测点的压力和压力梯度波形基本相同。因此，在后文缓冲结构对初始压缩波影响的研究中均采用距离隧道入口80 m 截面处测点3。列车车头进入隧道使得车前空气压力增大。距鼻尖2.7 m 车头横截面（即车头最大横截面积变化率部位）进入隧道洞口，车前压缩波压力持续增大，在t=0.130 8、0.188 4、0.246 0 和0.304 8 s 时刻分别传播至40、60、80 和 100 m 处测点截面。比较发现：当车头最大横截面积变化率部位进入隧道时，压力增量形成的压缩波使测点处的压力梯度达到最大。由于初始压缩波最大压力梯度与隧道微气压波幅值成正比，因此对于隧道微气压波而言，初始压缩波压力梯度的分布与头型横截面积沿车头长度方向的分布密切相关。针对本文头型微气压波优化而言，应尽量减少头型横截面积的突变部位，平顺头型更好。

图8 初始压缩波波形和最大压力梯度时间历程图Fig.8 Time history of initial compression wave and maximum pressure gradient

为进一步探究初始压缩波压力和压力梯度的产生机理，取距离隧道入口 80 m 截面处测点压力及其梯度和该截面处流量及其变化率进行分析。截面流量（即质量流量）的计算公式[26]如下：

式中：ρf为截面处空气密度，vf为截面处相对地面的面速度矢量，af为截面网格面积。当Q为负值时，表示流体从隧道入口流入截面；为正值时，则相反。

由图9（a）可知，列车进入隧道将隧道内空气排开向鼻前流动，使隧道截面流量不断增大，由于车头横截面积增加，导致阻塞比增加，排开空气的流速和流量增加，压力增加。由图9（b）和图8 可知，当车头最大横截面积变化率部位进入隧道洞口，阻塞比突增，车头排开空气的流速和流量突增并流入隧道，隧道内空气流量突增，使得流量变化率达到最大，压力梯度达到最大。由此可见，通过降低隧道内流入空气的变化率即可降低其初始压缩波的压力梯度，这为本文缓冲结构的设计提供了依据。

图9 初始压缩波波形和最大压力梯度的机理Fig.9 Mechanism of initial compression wave shape and maximum pressure gradient

2.2 扩大等截面无斜切缓冲结构的初始压缩波特征和形成机理分析

在隧道入口端加设无斜切端的扩大等截面缓冲结构（简称无斜切端缓冲结构），研究其对初始压缩波的影响。图10 展示了有、无缓冲结构下隧道内初始压缩波的形成过程。由图10（a）可知，当列车驶入隧道前，隧道内初始压缩波形成已经开始。A 点对应的是列车鼻尖到达隧道入口时刻；B 点对应的是列车鼻尖到达隧道入口产生的压缩波传播到测点的时刻；C 点对应的是车头最大横截面积变化率部位产生的压缩波传播到测点的时刻，此时压力梯度达到最大值（即E 点）；D 点对应的是车头流线型部位

完全进入隧道（列车进入隧道16 m）产生的压缩波传播到测点的时刻。曲线AD 段展示了初始压缩波形成的过程。在洞口增加无斜切端缓冲结构后，隧道内初始压缩波被分为两个阶段，如图10（b）所示。第一阶段为A'D'段：列车进入无斜切端缓冲结构产生初始压缩波，其原理与无缓冲结构时相似。第二阶段为D'G'段：列车在无斜切端缓冲结构中运行，隧道内压力缓慢上升，E'点对应的是列车鼻尖到达隧道入口产生的压缩波传播到测点的时刻；F'点对应的是列车驶入隧道 2.7 m 产生的压缩波传播到测点的时刻，此时压力梯度达到第二个峰值（即I'点）；G'点对应是车头流线型部位完全进入隧道产生的压缩波传播到测点的时刻。

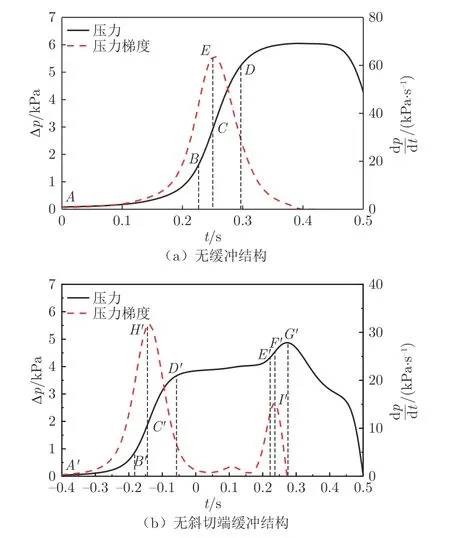
图10 有无缓冲结构下隧道内初始压缩波的形成过程Fig.10 The formation process of initial compression wave in tunnel with or without hood

图11 给出了无斜切端缓冲结构和无缓冲结构隧道内初始压缩波压力和压力梯度时间历程曲线。由图11（a）可知：有缓冲结构隧道内的压力上升有两个阶段，压力峰值为4.869 kPa，其对应的时刻为t=0.273 6 s。与无缓冲结构（压力峰值为6.025 kPa）相比，缓冲结构隧道内压力峰值明显降低，降低率为19.18%。针对压力梯度而言，如图11（b）所示：无斜切端缓冲结构隧道中的初始压缩波压力梯度有两个峰值，分别对应t=−0.138 0 和0.237 6 s，最大压力梯度为31.55 kPa/s。与无缓冲结构（最大压力梯度为63.00 kPa/s）相比，加设缓冲结构对压缩波最大压力梯度降低作用明显，最大降低率为49.92%。

图11 无斜切端缓冲结构与无缓冲结构隧道内初始压缩波压力和压力梯度时间历程曲线Fig.11 Time history curves of initial compression wave pressure and pressure gradient in an enlarged iso-section hood and hood without oblique port

图12 给出了无斜切端缓冲结构隧道内初始压缩波的压力及其梯度、流量及其变化率和列车及其产生的压力波轨迹图。其中，车头鼻尖和车头最大横截面积变化率部位从缓冲结构入口进入隧道16 m（一个鼻长的距离），由于阻塞比的突变分别在缓冲结构入口和隧道入口产生压缩波。由图可见，测点处产生了两个压力梯度峰值（即t=−0.138 0 和0.237 6 s 处），主要由车头最大横截面积变化率部位进入缓冲结构和隧道入口产生的压缩波引起。隧道内流量与压力规律相同，这是因为在列车进入缓冲结构/隧道过程中，车头横截面积变化导致了阻塞比、列车前方排开空气的流速、流量以及压力的改变。当车头最大横截面积变化率部位到达缓冲结构/隧道时，阻塞比突变，隧道内空气流量突增，流量变化率达到峰值，初始压缩波压力梯度达到峰值，所以流量变化率与压力梯度的峰值也是相对应的。

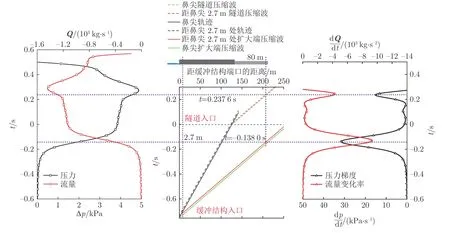
图12 无斜切端缓冲结构隧道初始压缩波形成机理Fig.12 Formation mechanism of initial compression wave in hood tunnel without oblique port

无斜切端缓冲结构能较大幅度降低初始压缩波最大压力梯度也可从隧道内空气流量及流量变化率变化特性角度进行定量分析，如图13所示。无斜切端缓冲结构隧道内空气流动比无缓冲结构隧道内平缓（图13（a）），空气流量最大值为1 440 kg/s，降低了20.66%（无缓冲结构隧道流量最大值为1 815 kg/s）。这是因为无斜切端缓冲结构使阻塞比减少，从而减少了隧道内空气流量，降低了初始压缩波压力幅值。在图13（b）中，无斜切端缓冲结构隧道内空气流量变化率最大值为9 335 kg/s2（此时流量为582 kg/s），无缓冲结构时为18 970 kg/s2（此时流量为910 kg/s）。相比无缓冲结构，有缓冲结构隧道内空气流量变化率最大值降低了50.79%。由此可见，在初始压缩波的压力梯度达到最大值时，无斜切端缓冲结构相比于无缓冲结构，空气流入隧道内更少，空气流量变化率也更低，所以初始压缩波压力梯度大幅降低。

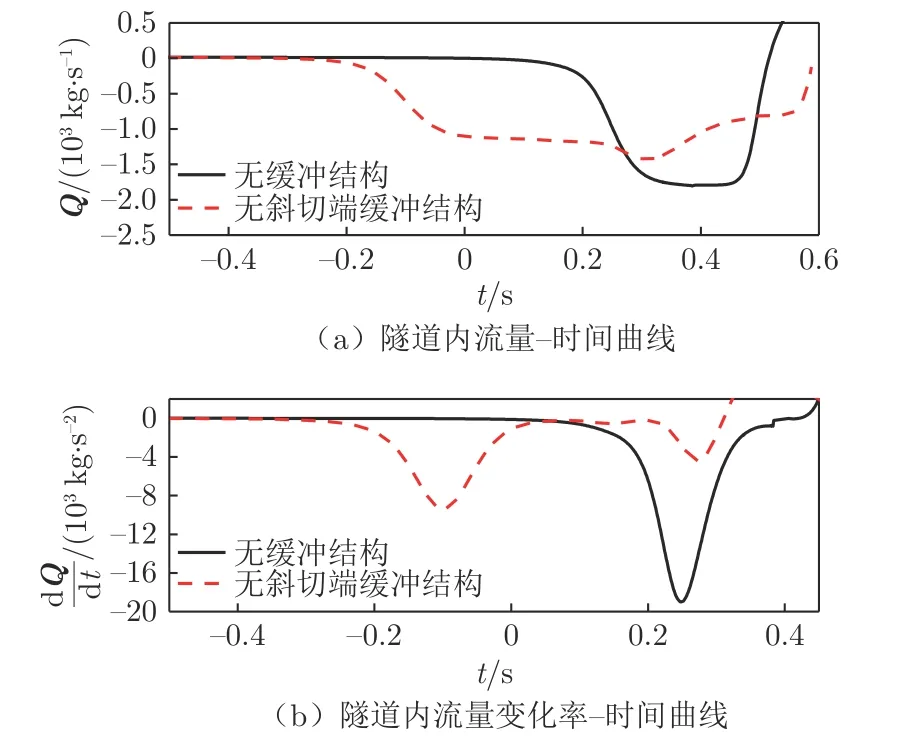
图13 无斜切端缓冲结构与无缓冲结构隧道内流量和流量变化率时间历程曲线Fig.13 Time history curves of the flow and flow rate in the tunnel of the hood and the hood without the oblique port

2.3 扩大等截面斜切型缓冲结构的初始压缩波特征和形成机理分析

在隧道缓冲结构端口型式中，斜切型、喇叭型和开孔型都可以降低初始压缩波的最大压力梯度。本文主要研究扩大等截面斜切型缓冲结构（简称有斜切端缓冲结构）对初始压缩波的影响。

图14 给出了斜切角θ=10°时，有、无斜切端缓冲结构和无缓冲结构隧道内初始压缩波压力及压力梯度时间历程曲线。由图14（a）可知：有斜切端与无斜切端缓冲结构相比，隧道中压力波形相似，有斜切端缓冲结构隧道内压力波形更加平缓。有斜切端缓冲结构隧道内压力最大值为4.258 kPa（t=0.272 4 s），相比无缓冲结构降低了29.32%，相比无斜切端缓冲结构降低了10.14%。在图14（b）中，有斜切端缓冲结构隧道内压力梯度曲线比无斜切端更加平缓。t=−0.154 4 s 时，有斜切端缓冲结构隧道内压力梯度达到最大值23.4 kPa/s。有斜切端缓冲结构隧道内压力梯度最大值比无缓冲结构隧道降低了62.85%，由此可见，有斜切端缓冲结构隧道内压力梯度最大值降低率相比于无斜切端缓冲结构提高了12.93%（无斜切端缓冲结构相比于无缓冲结构，隧道内压力梯度最大值降低了49.92%）。

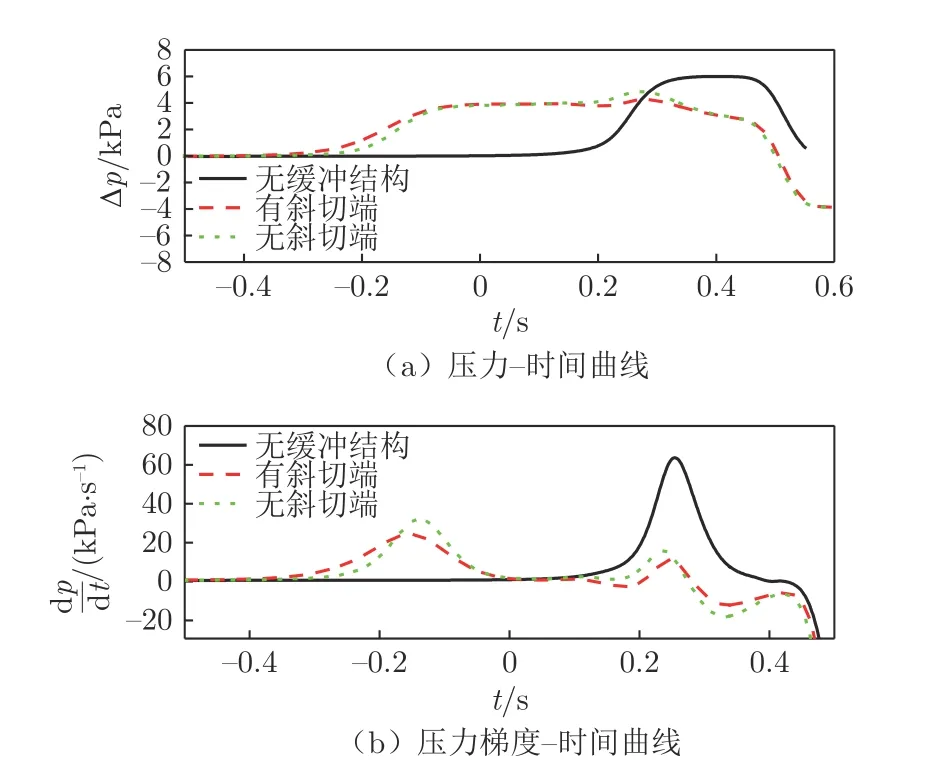
图14 有无斜切端缓冲结构和无缓冲结构隧道内初始压缩波压力及其梯度时间历程曲线Fig.14 Initial compression wave pressure and its gradient time history curves in the tunnel without hood and with hood and oblique hood

从轨迹图和流量角度阐述缓冲结构加斜切端能进一步降低初始压缩波最大压力梯度的原因。图15 给出了10°斜切角缓冲结构隧道内压力和压力梯度机理图。可以看到，斜切端横截面积变化率峰值范围为10～38 m。当t=−0.346 0 s 时，列车鼻尖到达距斜切端10 m（斜切端横截面积变化率最大范围开始）处，其产生的压缩波使测点压力开始第一次上升；当t=0.235 0 s 时，列车鼻尖到达隧道入口，测点压力开始第二次上升。初始压缩波压力梯度的两个峰值（t=−0.154 4 和0.247 2 s 时）分别由车头最大横截面积变化率部位到达距斜切端67 m 和隧道入口时产生的压缩波引起。列车进入斜切端时，由于车头横截面积和斜切端横截面积在不断变化，导致车头–斜切端耦合系统的阻塞比变化，列车前方排开的空气流速和流量变化，从而使得隧道压力变化，因此流量与压力曲线规律基本相同。车头最大横截面积变化率部位到达斜切端/隧道入口时，会导致车头–斜切端/隧道耦合系统的阻塞比突变，使隧道内空气流量突增，流量变化率达到峰值，造成初始压缩波压力梯度达到峰值，所以空气流量变化率峰值和压力梯度峰值相对应。

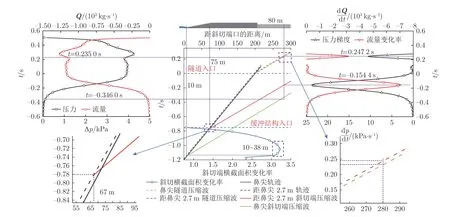
图15 10°斜切角缓冲结构隧道内压力和压力梯度形成机理Fig.15 Mechanism diagram of pressure and pressure gradient in the tunnel of hood with 10° oblique Angle

图16 给出了有、无斜切端缓冲结构和无缓冲结构隧道内流量和流量变化率的定量对比。在图16（a）中，有、无斜切端缓冲结构隧道内空气流量规律相似，有斜切端缓冲结构隧道内空气流量最大值为1 292 kg/s，相比无缓冲结构隧道降低28.81%，即缓冲结构如果增加斜切端可使隧道内空气流量再降低8.15%。这说明有斜切端缓冲结构可以更多地减少由于阻塞比变化导致的空气流量流入，从而使初始压缩波压力幅值降低得更多。在图16（b）中，有斜切端缓冲结构隧道内空气流量变化率最大值为7 049 kg/s2，比无缓冲结构隧道降低了62.84%，即缓冲结构如果增加斜切端可使隧道流量变化率再降低12.05%。这说明缓冲结构加斜切端可有效减少阻塞比突变，使隧道内空气流量变化率降低，所以有斜切端缓冲结构隧道内压力梯度最大值降低率比无斜切端缓冲结构隧道提高了12.93%。

图16 有、无斜切端缓冲结构和无缓冲结构隧道内流量和流量变化率时间历程曲线Fig.16 Time history curves of in-tunnel flow and flow rate in the tunnel without hood and with hood and oblique hood

2.4 斜切角度对缓冲效果的影响

图17 给出了不同斜切角度（θ=10°、20°、30°和39°）下，缓冲结构隧道内初始压缩波压力和压力梯度时间历程曲线。可以看到，在4 种不同斜切角度缓冲结构隧道中，压力波形规律基本一致。当斜切角度θ=39°、30°、20°和10°时，缓冲结构压力最大值分别为4.568、4.492、4.416 和4.258 kPa，压力最大值随着斜切角度减小而减小。当斜切角度θ=10°时，压力降低率最优，相比于无缓冲结构隧道，其压力降低率约为29.32%。在不同斜切角度缓冲结构下，隧道内初始压缩波压力梯度曲线规律相似。压力梯度最大值随着斜切角度减小而减小。当斜切角度θ=39°、30°、20°和10°时，缓冲结构隧道压力梯度最大值分别为27.6、26.4、25.0 和23.4 kPa/s，相比于无缓冲结构隧道，其压力梯度降低率分别为56.20%、58.10%、60.31%和62.85%（降低率变化跨度约2%）。

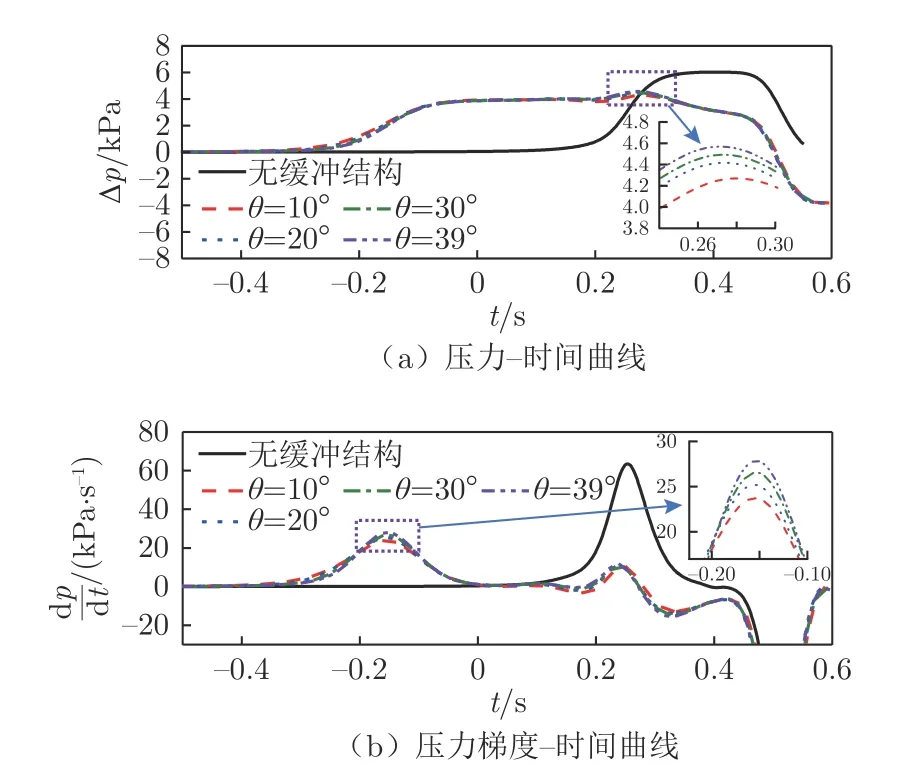
图17 不同斜切角度缓冲结构隧道内初始压缩波压力和压力梯度时间历程曲线Fig.17 Time history curves of initial compression wave pressure and pressure gradient in hood tunnel with different oblique angles

从空气流量及流量变化率角度，定量分析不同斜切角度使压力和压力梯度峰值降低的原因，如图18所示。

从图18（a）可以看到，斜切角度θ=10°、20°、30°和 39°时，隧道内流量最大值分别为1 292、1 311、1 334 和1 357 kg/s。相比于无缓冲结构，θ=10°时隧道内空气流量降低率最优（约28.81%）。由图6 可知，随着斜切角度θ减小，缓冲结构斜切端的横截面积变化率也随之减小。这说明越小的斜切端横截面积变化率可以更多地减少进入隧道内的空气流量，从而更多地降低初始压缩波压力的幅值。

在图18（b）中，当θ=39°、30°、20°和10°时，隧道内空气流量变化率最大值分别为8 274、7 892、7 489、7 049 kg/s2（相比无缓冲结构的降低率分别为56.38%、58.39%、60.52%、62.84%）。随着斜切角度θ的减小（从39°至10°），斜切端横截面积变化率越小，空气流量变化率降低率在每个跨度的增幅约2%，从而使初始压缩波压力梯度降低率在每个跨度的增幅约2%。

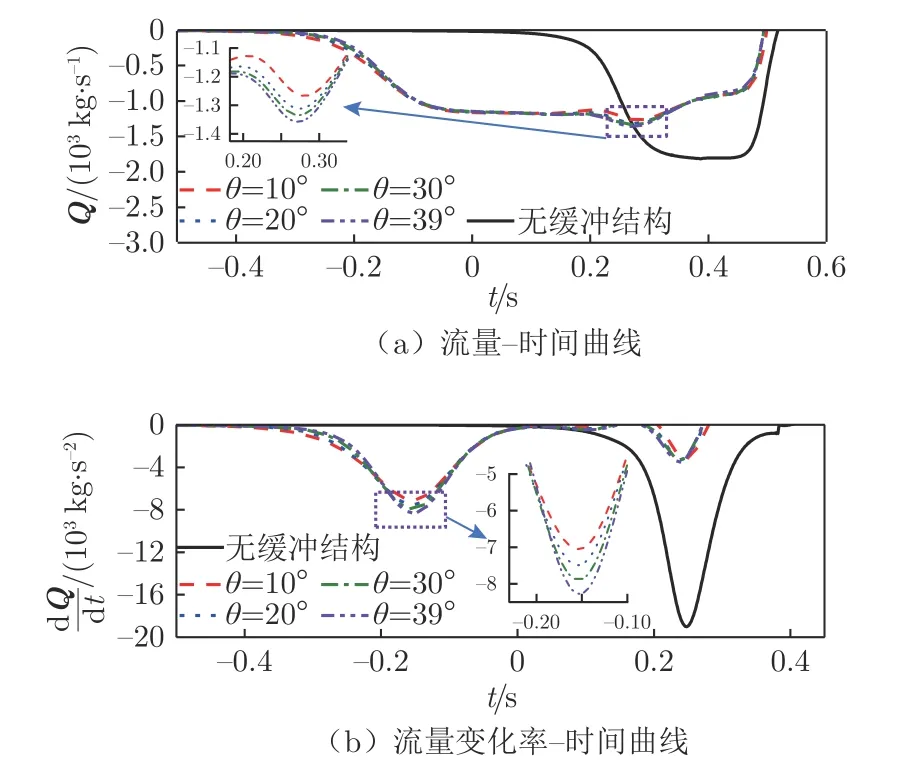
图18 不同斜切角度缓冲结构隧道内流量和流量变化率时间历程曲线Fig.18 Time history curves of flow and flow rate in hood tunnel with different oblique angles

3 结论

本文以600km/h磁浮列车为研究对象，基于三维非定常可压缩流动的雷诺平均N–S 方程和SST k–ω两方程湍流流动模型，进行了600km/h隧道扩大等截面斜切型缓冲结构减缓初始压缩波压力梯度的机理研究，主要结论如下：

1）车头最大横截面积变化率部位（距列车鼻尖2.7 m）进入隧道洞口会产生压力增量，当其形成的压缩波传播至测点处，初始压缩波压力梯度值最大。列车横截面积变化率呈现先增后减的规律，因此可以优化车头横截面积变化率，降低压力梯度的幅值。车头进入隧道，阻塞比开始变化，会使车头排开的空气流速和流量变化，导致隧道内流量变化，从而使隧道内压力变化。

2）扩大等截面缓冲结构降低了初始压缩波压力梯度，降低率为49.92%。相比于无缓冲结构，扩大等截面缓冲结构降低了由车头最大横截面积变化率部位进入缓冲结构造成的阻塞比突变最大值，从而减小了车头前排开空气流速和流量突变，导致隧道内流量变化率降低率为50.79%，有效降低了初始压缩波压力梯度。

3）缓冲结构加斜切端，能进一步降低初始压缩波的压力梯度。相比于无斜切端缓冲结构：10°斜切角缓冲结构能使隧道内压力梯度进一步降低12.93%；10°斜切角缓冲结构还可以缓解阻塞比的最大突变，降低车头前排开空气流速和流量突变，使隧道内空气流量变化率进一步降低12.05%。

4）随着斜切角度减小，斜切端横截面积变化率减小，隧道内空气流量变化率减小，隧道内初始压缩波的压力梯度最大值降低。当斜切角度θ=10°时，缓冲结构对隧道内初始压缩波最大压力梯度降低作用最明显，降低率为62.85%。

5）探究影响初始压缩波最大压力梯度的头型、空气流量之间的相互映射关系发现，列车头型和缓冲结构优化都可以降低初始压缩波的压力梯度，后者对初始压缩波压力梯度的缓解效果更加明显。