城市快速路单车道车头间距的研究
刘岩,邵岩
(1.大连交通大学 交通运输工程学院,辽宁 大连 116028;2.吉林大学 交通学院,吉林 长春 130025)*
0 引言
车头间距指的是在同一车道上行驶的车辆队列中,两个连续车辆车头端部间的瞬时距离.车头间距这个微观参量与速度、密度、流量三参数密切相关,车头间距根据交通量大小,将表现为不同特性,但是,从统计学角度看,车头间距分布均存在一定的分布规律.目前比较成熟和有代表性的分布模型主要有负指数分布、移位负指数分布、Cowan M3分布和K阶Erlang分布等[1-4].
本文主要研究车辆达到符合泊松分布,交通处于自由流状态下的车头间距分布规律,并且利用实测数据分析了车头间距与车型之间、车头间距与交通流之间的关系.最后得出在自由流状态下车头间距的分布符合负指数分布,车头间距与前后车车型有密切关系,车头间距与交通流量有密切关系.
1 车头间距分析
在实际的研究过程中,车头间距是很难直接测得的,而车头间距和车头时距是表述同一概念的不同量度单位,车头时距又是能够容易直接测得的,所以文章利用此关系把车头时距转换为车头间距来进行研究[5-6].
车头时距是指同向连续行驶的两辆车的车头通过道路某一断面时的时间间隔.车头时距是交通流率的倒数,可以得到车头时距与车头间距的转换关系式[7]:

式中,hs为车头间距,m/辆;ht为车头时距,s/辆;v为行驶速度,m/s.
在车头间距的研究中发现,由于混合车流车速差异,车流有“分离”和“压缩”状态存在.当流量小,由于随机度高,车流可按各自的技术车速行驶,当前后车序列为快慢排序,则相互间的间距会逐渐拉大,形成“分离”状态,此时,两车的间距可由后续快速车或合流区汇入车填补;当流量大,由于随机度小,超车的可能也减少,此时,如前后车序是以慢快排序,则快速车只能降低自己的速度跟随慢速车前进,此时,如前方有多余的道路空间,只能由相邻车道侧移或合流区汇入填补,当流量达到通过能力时,车辆跟随前进,行驶速度慢的车车速制约车流运动,产生“压缩”现象.在车头间距的模拟中,随机度的概念贯穿始终,车头间距研究为微观研究,而速度和流量却是表征交通流整体特征的宏观参数,通过随机度参数将微观和宏观参数整合为一体,避免了两种不同途径研究引起的脱节[8-11].
2 车头间距数据调查与处理
2.1 交通调查
文章使用数码摄像机连续拍摄车流运行状况,采集数据并且进行分析.交通调查地点选取鞍山市胜利路,选取的时间段是平峰,具体调查位置和调查方案如图1所示.

图1 交通调查方案图
为了避免转向车和合流分流车辆的影响,选择距离交叉口较远的路段,在内侧车道设置间隔2 m的两条基准线,调整摄像机摄取每个车辆通过基准线的时刻,进而能算出连续两辆车的车头时距,再利用式(1)可以得出车头间距.
2.2 数据处理
共采集到有效数据518个,所有样本的散点图如图2所示.
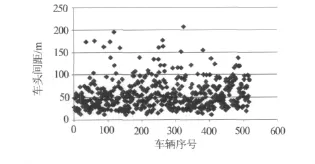
图2 车辆车头间距分布图

表1 车头间距分布表
从图2中无法看出车头时距的分布规律,下面应用数理统计方法来对数据进行处理,将样本按照一定的时间长度分组,将所得到的518个样本按照其车头时距时长分入各组,得出车头时距频率分布表,如表1.
将表1绘成柱状图得出车头时距分布频率图,如图3.

图3 车头间距分布频数图
车头间距分布与观测断面的交通量息息相关.不同道路的交通流,虽然同样属于连续流交通设施,但由于在运行特性上存在诸多不同之处,车头时距分布模型会有所不同,所适应的流量范围当然也会有所不同.文章采用χ2假设检验对实测数据进行拟合.
将车头间距按时间分组,分组统计情况如表1.
要检验数据是否符合负指数分布模型,则分布密度为:
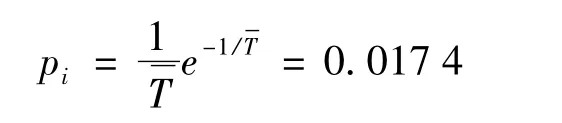
理论频数为:
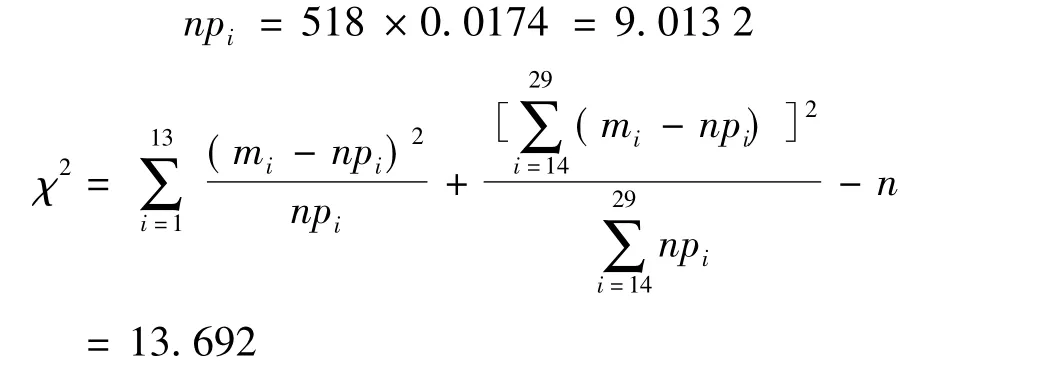
其中,mi为每组的车辆数.
由表1看出,110~170 m之间的车辆数大部分小于10辆,所以将他们分为一组,则自由度为:
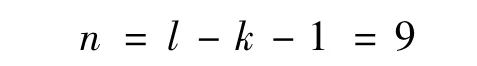
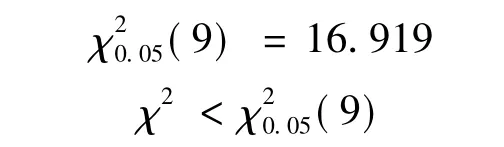
所以符合负指数分布.
3 车头间距数据分析
由于车头间距与交通流中各自成对的车辆有关,所以与交通流三参数关系相比,常被认为在这些特征是“微观”的,实际上由于车头间距的随机性,在任何交通流中,各自车头间距都分布在一定的数值范围之内,而且与交通流的速度和运行条件有关,尤其是在混合车流条件下,车头间距的分布与车型密切相关.
文章选取城市中最常见的车型——出租车和小汽车进行分析,小汽车和出租车的车头间距各种组合见图4、图5、图6,分析一下出租车与小汽车之间不同组合的车头间距分布规律.
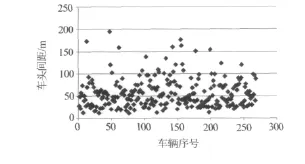
图4 小汽车—小汽车组合车头间距分布图

图5 小汽车—出租车组合车头间距分布图
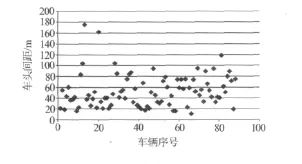
图6 出租车—小汽车组合分布图
小汽车和出租车之间不同组合的平均车头间距如表2所示:

表2 小汽车-出租车不同组合下的平均车头时距
从表2中可知出租车与小汽车之间的,后车为出租车、前车为小汽车的平均车头间距最大,为60.83 m;而后车为小汽车、前车为出租车的平均车头间距最小,为52.97 m.
分析其主要的原因:当出租车跟随小汽车时,后车对前车的驾驶行为没有很好的预判性和信任性,所以需要保持较大的车头间距;而当小汽车跟随出租车时,后车对于前车的驾驶行为有很好的预判性和信任性,所以后车可以尽可能地减少两车之间的车头间距.
此外,通过对实测数据分析,在自由流状态下,车流流量较小时,车速较快,平均车头时距较大;反之,车流流量较大时,车速较慢,平均车头时距较小.
4 结论
综上所述,可以得出以下结论:
(1)当车辆的到达符合泊松分布,车流密度不大时,车头间距符合负指数分布;
(2)当前车为小汽车、后车为出租车时,车头间距较大;而前车为出租车、后车为小汽车时,车头间距较小;
(3)车头间距与流量成反比关系,车流中平均车头间距越大,流量越小,反之,车流中平均车头间距越小,流量越大.
[1]罗霞,杜进有,霍娅敏.车头间距分布规律的研究[J].西南交通大学报,2001,36(2):113-116.
[2]Salter R J.Highway traffic analysis and design[M].Washington ACMILIAN,1989:216-243.
[3]王殿海.交通流理论[M].北京:人民交通出版社,2002:9-19.
[4]张智勇,黄轶,任福田.稳定跟车状态车头间距分析方法[J].北京工业大学学报,2010,36(2):219-222.
[5]王殿海,杨少辉,景春光.累计曲线法计算饱和流率和相位损失时间[J].交通运输工程学报,2003(3):75-78.
[6]杨小宝,张宁.一种改进的跟驰状态判定方法[J].交通运输系统工程与信息,2006(2):34-38.
[7]任福田,刘小明,荣建.交通工程学[M].北京:人民交通出版社,2003:107-115.
[8]周杲尧.高速公路路段车流运行模拟及评价研究[D].南京:东南大学,2005.
[9]苗贵华.国道G4改扩建工程施工交通组织方案优化与仿真研究[D].长沙:长沙理工大学,2008.
[10]段涵.山区高速公路特定纵坡路段车辆折算系数仿真研究[D].西安:长安大学,2009.
[11]陈洪仁,杨龙海,李丽兰.基于速度和车头时距的车辆换算系数计算方法研究[J].哈尔滨建筑大学学报,2001(2):110-114.

