混杂系统稳定性条件扩展及等价分析

李卫东，王中科

(大连交通大学 电气信息学院，辽宁 大连 116028)*

0 引言

混杂动态系统(Hybrid Dynamic Systems)是研究同时包含连续变量动态过程和离散事件动态过程的复杂系统，其混杂特性表现为连续变量和离散事件的相互作用［1-2］.混杂系统具有复杂性和特殊性，即便每个子系统是稳定的，混杂系统也不一定稳定;相反，如果有的子系统不稳定，那也不代表混杂系统是不稳定的［3］.稳定性分析及综合是控制系统研究的基本问题，不论在理论上还是在实践中均有重要意义，且实际运行的系统一般都要求是稳定的.因此，自从混杂系统提出以来，稳定性问题便受到了研究人员的广泛重视，近些年在混杂系统稳定性方面取得的理论成果也是颇为丰富的［4-5］.目前，在混杂系统的稳定性研究中，主要有Lyapunov意义下的稳定性和Lagrange意义下的稳定性两类.本文主要研究Lyapunov意义下的稳定性问题，同时为了使分析系统的稳定性问题能够得到简化，文中把稳定性条件等价为求解线性矩阵不等式的问题，同时借助了已有的计算机工具来进行了辅助分析.

1 系统模型

本文讨论了一类自治切换混杂系统，其控制器被设计成一个闭环的混杂系统.其方程描述如下:

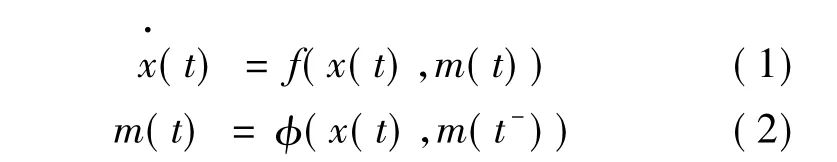
式中，x∈Rn，m∈M={m1，…，mN}，这里x表示连续状态，m表示离散状态，混合状态空间H=Rn×M.该混杂系统模型的初始条件是(x0，m0)∈I0，I0表示所有可能初始条件的集合.切换集可以表示为如下形式:

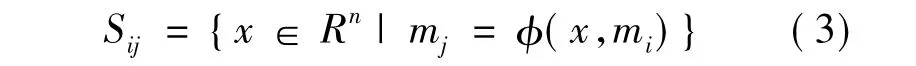
每一个f(*，mi)表示一个子系统，当m的值改变的时候会导致向量场f发生改变.系统的变化过程可概括如下:由起始点处(x0，m0)，当m0=mi，在时刻t0，演变轨迹可由x·=f(x，mi)得出.当x在t1时刻，其状态变为(x1，mj)，变化曲线可由x·=f(x，mj)得出.为了使混杂系统稳定性条件体现在函数f和φ中，前提是对于任意初始条件都存在使系统趋于稳定的条件，且f(x，mi)∀mi∈ M 是连续的［6］.

2 理论分析

2.1 稳定性理论

定义1 一个连续的函数α:R+→R+，满足以下条件:

(1)α(0)=0;

(2)α(z)＞0，∀z＞0;

(3)α(z1)≤ α(z2)，z1＜ z2.则称函数α为K类函数.

定理1 (Lyapunov稳定性定理)若存在函数V:Rn×R→R以及K类函数α:R+→R+，β:R+→R+满足如下条件:

(1)α(‖x‖)≤ V(x，t)≤ β(‖x‖)

(2)∀t≥ t0，V(x，t)≤ h(V(x0，t0))，h∈C［R+，R+］，h(0)=0，R+= ［0，+ ∞)(函数 h 引用于文献［7］)

则系统在平衡点0处是处于Lyapunov意义下的稳定状态.若‖x‖→∞ 时，α(‖x‖)→∞则系统在平衡点0处是全局稳定的.

假设混杂系统(1)、(2)中的混杂状态空间分为 l个不相交的区域 Ωq，q=1，…，l，Ωq既可以是有界的也可能是无界的，在每个区域Ωq中有函数Vq(x，t)作为系统的能量函数.为了在区域Ωq得到唯一的连续状态，这里假定:

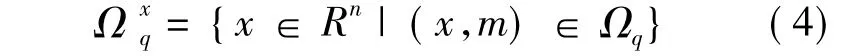
当 (x，m)∈ Ωq时，V(x，t)=Vq(x，t)，且假定初始状态是(x0，m0)∈ I0，能量是V(x0，t0).进而得出如下推论:

推论1 如果存在能量函数Vq(x，t)，以及K类函数α:R+→R+，β:R+→R+满足如下条件:

(1)∀(x，m)∈ Ωq，α(‖x‖)≤Vq(x，t)≤β(‖x‖)，q=1，…，l

(2)∀(x，m)∈ Ωq，∀t ≥ t0，Vq(x，t)≤h(V(x0，t0))，q=1，…，l

则系统在平衡点0处是处于Lyapunov意义下的稳定状态.

推论2 如果存在能量函数Vq:×R→R，q=1，…，l与时间无关，且每个能量函数Vq(x)对x(∀x ∈ Ωxq，q=1，…，l)可微，满足如下条件，(1)∀x∈，α(‖x‖)≤ Vq(x，t)≤β(‖x‖)，q=1，…，l

(2)∀(x，m)∈ Ωq，(x)≤ 0，q=1，…，l

(3)∀x∈ Ωqr，Vr(x)≤ Vq(x)，q=1，…，l，r=1，…，l

其中，α:R+→ R+，β:R+→ R+为 K 类函数，Ωqr表示系统从状态区域Ωq进入到Ωr，则系统在平衡点0处是处于Lyapunov意义下的稳定状态.

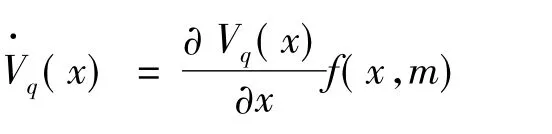
2.2 等价线性矩阵不等式分析

引理1 一个向量场f:Rn→Rn可以表示为如下形式:

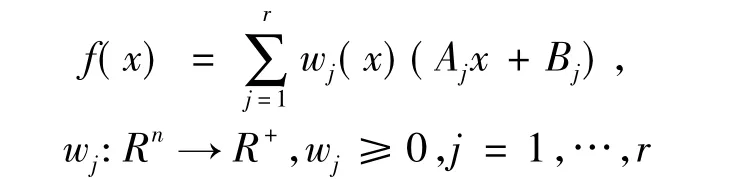
根据上述引理可以把所有非线性子系统f(*，mi)，mi∈M通过加权的线性子系统来表示，形式如下:

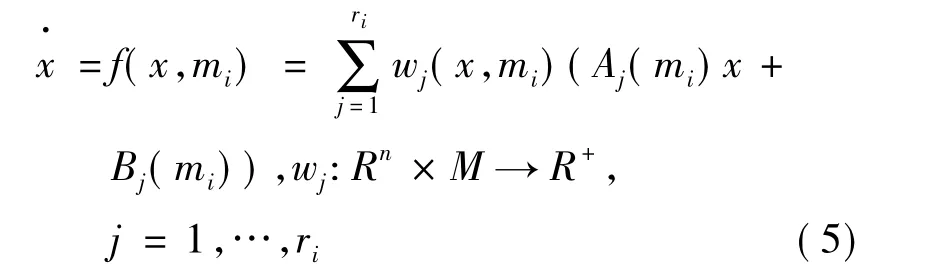
为了把系统稳定性条件转化成为求解线性矩阵不等式的问题，这里考虑把能量函数表示为如下形式:

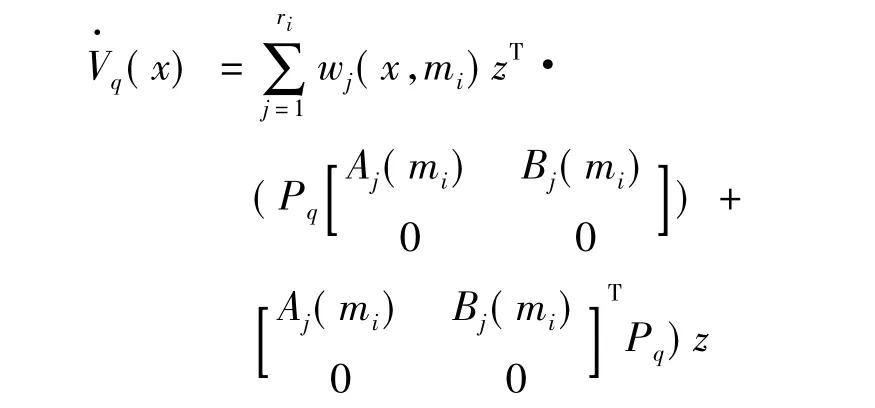
从而可以得出以下推论:

推论3 如果存在矩阵 Pq，q=1，…，l，α ＞0，β＞0，满足如下条件:

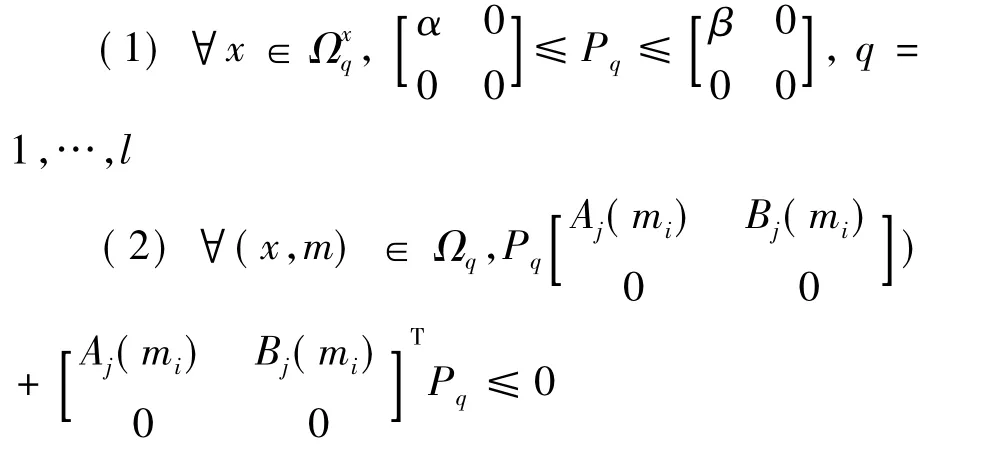
(3)∀x ∈ Ωqr，Pr≤ Pq，q，r=1，…，l

系统在平衡点0处是Lyapunov意义下的全局稳定状态.

3 仿真分析

考虑如下两个包含离散状态的混杂系统:

其中切换集为S12={x∈R2|x2=0}，S21={x∈ R2|x2=0.5x1}，初始状态设为(x0，m0)=(［－ 5，5］T，m1)，系统的状态变化曲线如图1所示，从图中可见该混杂系统趋于0点的稳定状态.

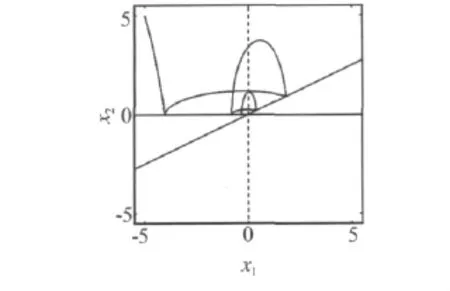
图1 混杂系统状态变化曲线

通过引理1可以把系统描述为如下形式:

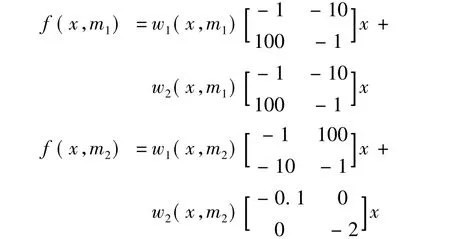
根据推论3可以求得

能量函数的变化曲线如图2所示，从图中可以看出能量函数随时间推移呈递减趋势，即系统满足稳定性条件，从而证明了所提出理论是可行的.

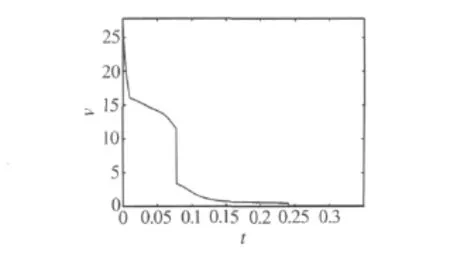
图2 能量函数变化仿真图形

4 结论

混杂系统中的稳定性问题是研究人员关注的重点内容之一，且已经在许多文献中进行了阐述和分析.本文通过对经典稳定性理论进行扩展，给出了含有非线性子系统的自治切换混杂系统的稳定性判据.随后，把稳定性问题等价转化为线性矩阵不等式的问题，进而利用便利的计算机工具对给出的实例进行了仿真分析，通过仿真结果验证了所提出理论的正确性及分析方法的有效性.

［1］莫以为，萧德云.混合动态系统及其应用综述［J］.控制理论与应用，2002，19(1):1-8.

［2］MORSE A S，PANTELIDES C C.Introduction to the Special Issue on Hybrid Systems ［J］.Automatics，1999，35(3):347-348.

［3］BRANICKY M S.Multiple Lyapunov Functions and other analysis tools for switched and hybrid systems［J］.IEEE Trans.Automat.Contr，1998，43(4):475-482.

［4］DECARLO R A，BRANICKY M S，PATTERSON S，et al.Perspectives and results on the stability and stabilizability of hybrid systems［J］.Proceedings of the IEEE，2000，88(7):1069-1082.

［5］DAVRAZOS G N，KOUSSOULAS N T.A Review of Stability Results for Switched and Hybrid Systems［C］.Dubrovnik，9th Mediterranean Conference on Control and Automation，2001:235-244.

［6］SLOTINE J E，LI W.Applied Nonlinear Control［J］.Prentice-Hall，2003，18(2):25-38.

［7］YE H，MICHEL A N，HOU L.Stability theory for hybrid dynamical systems［C］.Croatia，In Proc.of 34th CDC，1999:2679-2684.