交流电机调速系统的分数阶PIλ控制
聂冰,赵慧敏,郭永香,李文
(大连交通大学 软件学院,辽宁 大连 116028)*
0 引言
整数阶PID控制器具有操作简单、调整方便、鲁棒性好等特点,在电机控制应用中处于主导地位,但是随着控制对象的机构越来越复杂,控制参数越来越多,常规的整数阶PID控制往往难以得到满意的控制效果[1].分数阶PID控制器是传统整数阶PID控制器的扩展,由于它具有更多的可调节参数,故为复杂的被控对象带来了更加灵活的参数调节能力,使其具有更好的控制特性.
交流电机作为工业控制领域的重要电气设备被广泛应用,电机传动系统是一个复杂的动力机械系统,其中存在着很多非线性因素,如齿轮间的间隙和摩擦、基础振动等,因此,系统的分数阶特性变得无法忽略.为了降低交流电机传动系统的噪声与振动,进一步扩展传统的整数阶控制方法,在交流电机传动系统中引入分数阶控制是可行和必要的[2],具有实际意义和应用价值.
本文主要讨论了交流电机调速系统的分数阶PIλ控制.首先介绍了分数阶微积分的基本含义,并将其应用到分数阶PIλ控制器的设计.在交流电机调速系统中使用分数阶PIλ控制器进行控制,通过测试实验表明分数阶PIλ控制器的可行性及其有效性.
1 分数阶微积分
分数阶微积分的一般定义为[3]:
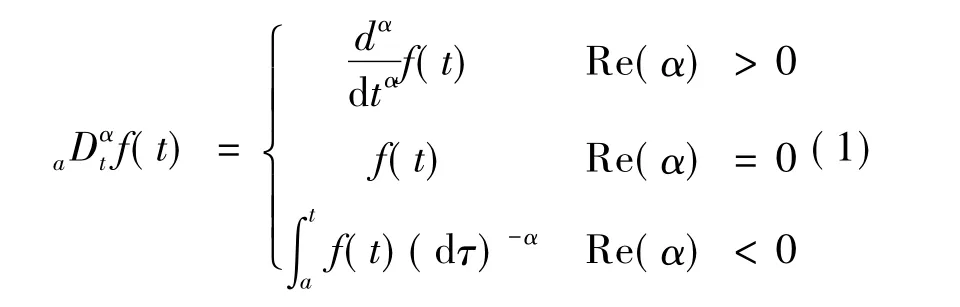
式中,a和t为算子a的上下限,微积分算子是函数f(t)的α次积分或导数.
分数阶微积分中α是任意数,常用的分数阶微积分定义是Grünwald-Letnikov,其微积分定义为:

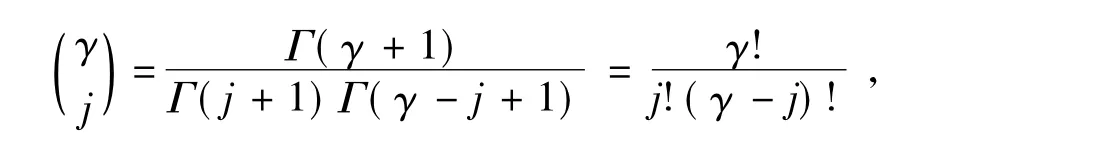
h为计算步长.
RL是另一种分数阶微积分的定义.与GL定义相比,RL分数阶微积分的计算更为简化,其分数阶微积分的定义为:
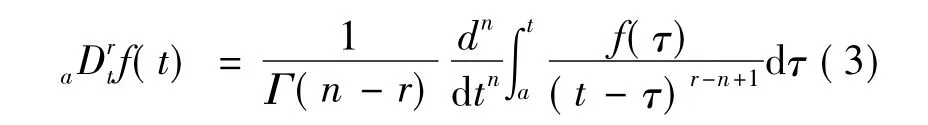
2 分数阶PIλ控制器
2.1 分数阶PIλ控制器的设计
整数阶PIλ控制器传递函数为:
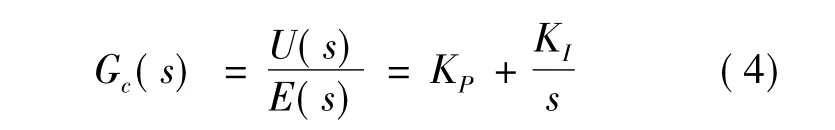
式中,U(s)为控制器的输出;E(s)为控制器的误差输入.分数阶控制系统是整数阶控制系统的扩展,将式(4)推广到分数,其分数阶PIλ控制器的传递函数为:
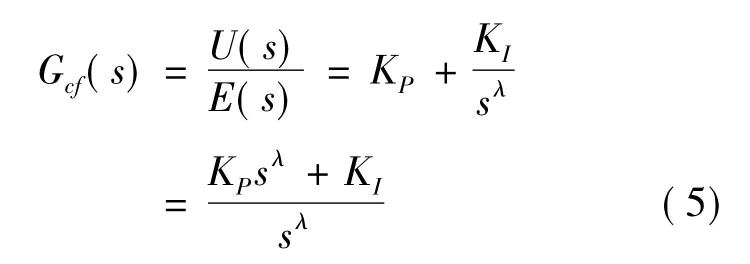
式中,KP、KI为控制器的控制参数,λ>0是分数阶控制器的积分阶次,可表示为任意实数.
2.2 分数阶PIλ控制器的离散化
分数阶控制器是无限阶次,其设计的关键问题是解分数阶微积分方程时需要对微积分算子进行离散化.离散化方法主要使用直接离散化和间接离散化,直接离散化应用更为广泛[2].直接离散化法的基本思想是:分数阶微积分sr用生成函数 s= ω(z-1)来表示,将r次无理函数 ωr(z-1)在离散时间域Z中使用有限阶次的有理函数对其进行逼近[2,4].目前常用的分数阶积分算子包括:Rectangular算子、Tustin算子和Simpson算子及由Al-Alaoui提出的算子.连分式(CFE)是对函数或数值的一种有效近似形式,它的展开比通常线性展开收敛速度更快.Tustin算子具有很好的相位特性和简单的结构,利用Tustin算子进行连分式(CFE)展开是一种有效的离散方法[5-6].根据Tustin算子得到阶次为r的生成函数为:

将该生成函数应用收敛速度快的连分式展开,对其进行分数阶微积分算子的近似,得到了效果更理想的分数阶数字积分器.
离散函数G(z)可以用连分式展开式近似展开,形式表示如下所示:
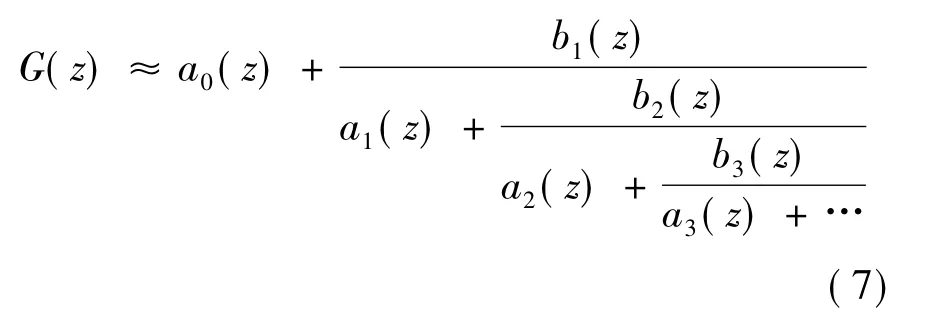
式中,ai(z)和bi(z)为常量或z的有理函数.

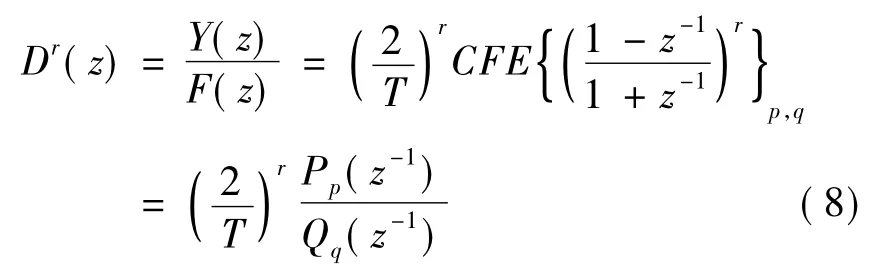
式中,r∈[-1,1],CFE{u}表示对函数u进行连分式展开,P和Q是变量z-1多项式,一般展开阶次 p=q=n,得到近似等式[3]:
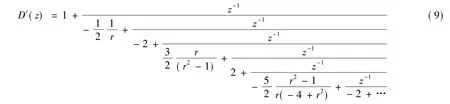
附表列出了当近似阶次p=q=1,3,5取不同值时,分数阶积分器的分子分母近似表达式.
根据经验,综合考虑系统的计算能力和控制性能要求选取近似模型的阶次为3,分数阶微积分sr的离散化模型为:
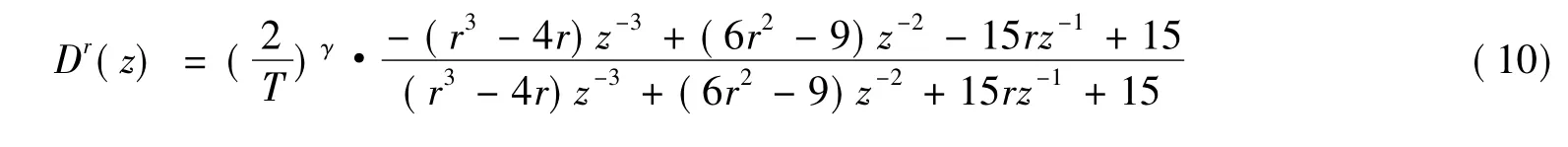

附表 Dr(z)分子分母的近似表达式
3 应用实例
使用离散的分数阶PIλ控制器和传统整数阶PID控制器对交流感应电机调速系统进行控制.该系统硬件主要采用工控机,三相异步电动机,变频器,速度传感器及NI公司的数据采集模块,其配置框图如图1所示:
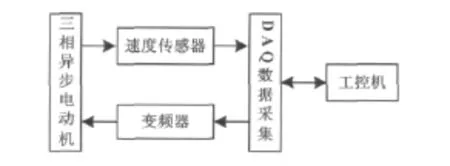
图1 交流电机调速系统配置图
根据经验,分数阶PIλ控制器控制参数分别为:Kp=0.24,ki=0.05,λ =0.47,采样周期T=1 s,采用Tustin+CFE离散方法,逼近阶次为3,分数阶PIλ控制器和整数阶PID控制器控制效果如图2所示.
图2分别为交流电机额定转速在300 r/min和600 r/min时,分数阶PIλ控制器和整数阶PID控制器控制效果对比图,其中虚线为分数阶控制器,实线为整数阶控制器.如图所示,在控制过程中,分数阶PIλ控制器和整数阶PID控制器的超调量几乎相同,但是分数阶控制器的调节时间更短,在电机平稳运行后,分数阶控制器要比整数阶控制器对电机的控制更加的平稳,振荡小,这种趋势随着时间的推移越发的明显,控制效果更好.
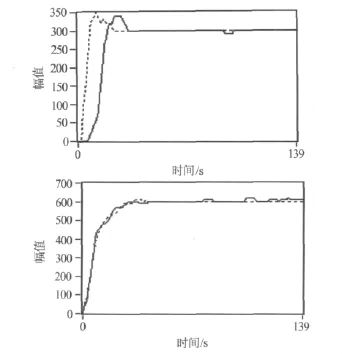
图2 分数阶控制器和整数阶控制器控制效果对比图
实验结果表明了分数阶PIλ控制器的有效性,进一步拓宽PID控制器的参数选择范围,为工程实际应用提供了可能.
[1]张邦楚,王少锋.飞航导弹分数阶PID控制及其数字实现[J].宇航学报,2005,26(5):653-656.
[2]赵慧敏,李文.一类分数阶滤波器逼近阶次的选择[J].电机与控制学报,2010(1):90-94.
[3]白晶.分数阶模型的离散化方法研究[D].大连:大连交通大学,2009.
[4]曹军义,曹秉刚.分数阶控制器的数字实现及其特性[J].控制理论与应用,2006,3(5):791-794.
[5]樊玉华,李文.分数阶微分算子的离散化方法比较[J].大连交通大学学报,2008,29(3):95-98.
[6]CHEN YANGQUAN.A new discretization method for fractional order differentiators via continued fraction expansion[C].2003 ASME International Design Engineering Technical Conferences,Chicago,USA,2003:1-9.

