基于Vold-Kalman滤波的阶次分析系统设计与实现*
昝 涛,刘智豪,王 辉,庞兆亮
(北京工业大学 机电学院 先进制造技术北京市重点实验室,北京 100124)
0 引言
由于阶次分析在处理非平稳信号时的独有特点,尤其是在设备升降速等变速阶段时,能够有效避免传统频谱分析产生的“频率模糊”现象。因此,阶次分析在设备监测、故障诊断和车辆噪声源定位等领域得到了广泛应用[1-2]。现在国内外阶次分析方法主要有两类:传统阶次分析技术和现代阶次分析技术。其中传统计算阶次分析技术有较多缺陷,表现为分辨率低与无法分辨密集阶次。而现代阶次分析技术中的Vold-Kalman滤波阶次分析法,可以很好的避免重采样带来的相位偏差,更重要的是其能有效分离邻近阶次,从而提高阶次分辨率[3-5]。
众多学者和技术人员在故障诊断领域广泛采用阶次分析技术。康海英等应用阶次分析和经验模式分解相结合的方法诊断齿轮故障[6],取得了良好的结果;王民等采用阶次分析和试验模态测试相结合的方法对电主轴运行状态进行振动测试与分析,研究导致高速电主轴高速运行中振动加剧的原因[7];Urresty等采用Vold-Kalman阶次分析诊断永磁同步机械的匝间故障[8],能对故障进行有效诊断;Mehmet Akar利用阶次分析诊断闭环感应异步电动机故障[9];Pelant等利用Vold-Kalman阶次分析诊断车内噪声与振动[10]。上述工程应用中,大多采用诸如LMS公司的SCADAS系统、B&K公司的阶次分析仪等国外专用设备,但是这些设备硬件价格十分昂贵,且配套软件较为封闭。因此,基于成本低开发快的虚拟仪器技术[11],设计实现Vold-Kalman滤波阶次分析系统具有重要意义。
本文在传统计算阶次分析的基础上引入Vold-Kalman滤波阶次分析理论,能有效解决传统计算阶次分析分辨率低,且无法分辨密集阶次等缺陷,从而大幅提高三维阶次谱图分辨率。对复杂机械系统的故障诊断有重要意义。本文依托LabVIEW虚拟仪器开发平台,设计了一套阶次分析系统,利用并行处理技术克服阶次提取时矩阵运算耗时较长的缺陷。该系统在实际的应用中取得良好效果。
1 阶次分析原理
1.1 计算阶次分析
计算阶次分析技术是在硬件阶次分析技术的基础上发展而来的,利用转速脉冲信号计算出重采样时间点,实现信号的重采样。用该方法替代直接使用硬件设备实现信号的等角度间隔采样。
具体步骤如图1所示。先以恒定时间间隔Δt同步采集被测量机械的振动信号和转速脉冲信号,即对原始数据进行第1次采样,得到原始采样信号。然后利用转速脉冲信号计算出以恒定角度间隔Δθ采样的触发时刻。其采样时间间隔会随着转速的变化而变化,对原始数据进行第2次采样即重采样,将等时间间隔的采样转变成等角度间隔的采样,再进行傅里叶变换,即可获得阶次谱[12]。

图1 等角度重采样
1.2 Vold-Kalman滤波阶次分析
利用上述计算阶次分析算法可以获得三维阶次谱图。但因其在分析转速变化较快的信号时,阶次分辨率低且无法分辨密集阶次,故引入Vold-Kalman滤波阶次分析技术解决上述问题。Vold-Kalman滤波阶次分析方法实质上是自适应滤波,振动信号经中心频率变化的带通滤波器得到期望的阶次成分,因信号未经时频变换,没有造成相位偏差和能量泄漏[13]。此方法由下面的结构方程和数据方程构成[14-15]。
1.2.1 结构方程
Vold-Kalman滤波阶次分析结构方程为:
x(n)-2 cos(ωΔT)x(n-1)+x(n-2)=0
(1)
式中,x(n)为待分析的阶次分量,ω为此阶次分量角频率,ΔT为采样时间间隔。
在实际应用中,所分析的目标阶次中总是掺杂着噪声和其他谐波信号。因此引入非均匀项ε(n), 式(1)变为:
x(n)-2 cos(ωΔT)x(n-1)+x(n-2)=ε(n)
(2)
1.2.2 数据方程
旋转机械运行过程中测量得到的动态信号y(n)可以表示为:
y(n)=x(n)+η(n)
(3)
此即Vold-Kalman滤波阶次分析技术的数据方程,其中η(n)代表非关心阶次分量与随机噪声之和。
1.2.3 阶次成分求解
式(2)和式(3)将待分析的阶次成分和在特定时间点的测量信号联系起来。对于长度为N的测量信号y(n),可以扩展方程(2)和方程(3)即:

(4)
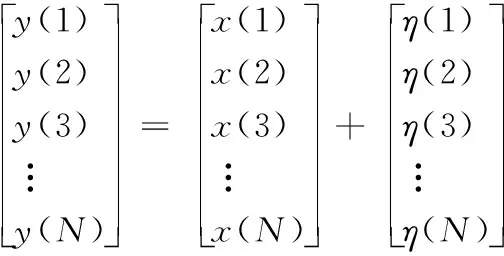
(5)
式中,c=2 cos(ωΔT)。式(4)和式(5)可分别简化为:
Ax=ε
(6)
y=x+η
(7)
式中,A为参数矩阵,x为被分析的阶次成分,y为测量信号,ε为非均匀项,η为其它非相干成分。
运用最小二乘法使结构方程和数据方程误差最小。引入权重因子r,使结构方程和数据方程的加权和如下:
J=r2εTε+ηTη
(8)
其中,r2εTε=r2xTATAx。令∂J/∂x=0,得到如下结果:
(r2ATA+I)x=y
(9)
待分析的阶次成分x通过上式解出,调节权重因子可得到不同的阶次分辨率。
2 系统设计
2.1 系统总体设计
本阶次分析系统由硬件部分和软件部分共同组成,其中主要包含3个模块,分别为传感器模块、数据采集模块和数据分析模块。总体方案设计如图2所示。
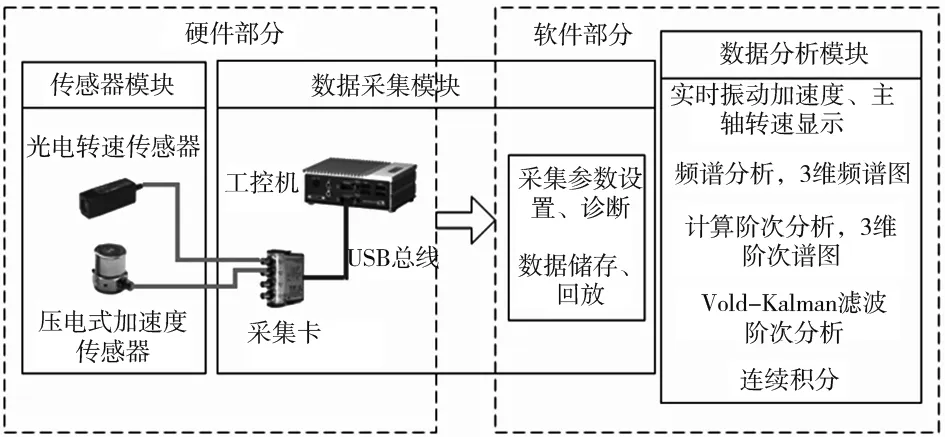
图2 系统总体设计方案
2.2 系统硬件设计
系统硬件部分主要包括传感器和数据采集卡。其中传感器依据阶次分析需要,考虑量程、灵敏度、频响、温度、输出电压等因素,选用CA-YD-186型加速计。采集卡考虑通道数、分辨率、带宽、输入范围、信号调理功能等因素,选用NI USB-9234型数据采集卡。
2.3 系统软件设计
本阶次分析系统软件流程图如图3所示。完成硬件连接后,启动软件进行系统硬件及采样信息等参数的设置。后系统进行参数自检,设置合格可进行后续分析,不合格需根据系统提示校正。在分析前,需选择运行模式在线采集或历史数据分析。运行在线采集模式时,窗口显示实时振动信号与主轴转速信号。成功获取数据后,开始数据分析。根据用户需要,保存原始数据与分析结果。
系统功能齐全具备实时绘制原始信号波形、频谱、阶次谱、三维频谱、三维阶次谱、阶次切片、故障预测、连续积分变换和数据管理等功能。

图3 系统运行流程图
其中计算阶次分析和Vold-Kalman滤波阶次分析功能是本系统核心,其算法LabVIEW实现程序框图分别如图4和图5所示。图4中上方程序对原始信号进行短时傅里叶变换绘制三维频谱图,下方for循环实现信号的等角度重采样,之后进行短时傅里叶变换绘制三维阶次谱图。图5中利用内嵌的for循环获得式(9)中的矩阵A,之后计算ATA,最后利用下方程序解出待分析的阶次x。此3步利用流水线技术实现并行处理,克服阶次提取时大量矩阵运算耗时长的缺陷。较优化前的算法提高运行效率近60%。

图4 计算阶次分析程序框图
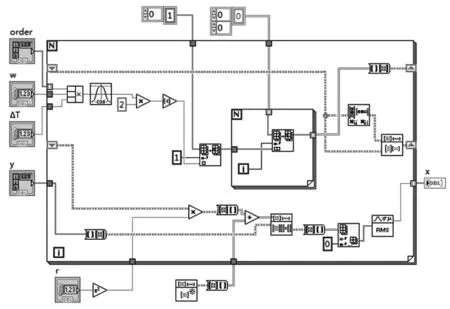
图5 Vold-Kalman滤波阶次分析程序框图
依据操作简便快捷高效、界面美观大方、人机交互友好等UI设计原则,加之仪器功能需求,设计系统主界面如图6所示。系统界面整体简洁美观、操作快捷方便。

图6 系统主界面
3 系统应用
3.1 Vold-Kalman滤波阶次分析效果
为验证Vold-Kalman滤波阶次分析方法的优越性,设计一个包含4个阶次成分的仿真信号,模拟临近阶次与交叉阶次,其阶次成分为8、8.5、9和1.2sin(n/6)+8.5阶,其中n为转频。
图7为Vold-Kalman滤波阶次分析方法与传统计算阶次分析对比图。如图利用Vold-Kalman滤波理论进行阶次分析比传统计算阶次分析获得的三维阶次谱图更加清晰,可大幅提高阶次分辨率,克服其无法分辨密集阶次与交叉阶次的缺陷,利于确定具体阶次。

(a) 计算阶次分析效果

(b) Vold-Kalman滤波阶次分析效果 图7 效果对比图
3.2 主轴试验台测试
为验证本阶次分析系统的正确性和可靠性,对系统进行了实际应用。测试对象为实验室某主轴试验台。将传感器安放在试验台适当位置。设置灵敏度102.8mV/g,采样频率6400Hz。启动软件开始采集信号,控制主轴转速由50r/min,每间隔1s增加50r/min,至2400r/min后停止。
图8分别为原始振动信号及其直接经过傅里叶变换得到的频谱。图9分别为等角度重采样后的振动信号及其阶次谱。在原始信号中,出现多个峰值,其原因是:转速不断增加,使主轴转频或其倍频不断增加,导致这一激励频率经历了结构的多个固有频率,使结构产生多次不同阶的共振。此时在其频谱图中出现严重的“频率模糊”现象,特征频率自500Hz“涂抹”到1000Hz,致使从频谱图中无法得到有用信息。
但在阶次谱中只有40阶这一条明显的谱线,即激励频率应为主轴转频的40倍。阶次分析有效的解决了传统频谱分析产生的“频率模糊”问题,清晰的揭示了信号内涵,充分体现了阶次分析处理非平稳信号时的优势。

(a) 原始振动信号
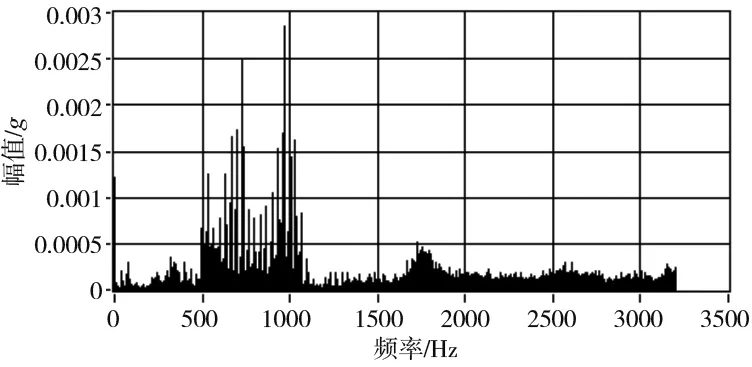
(b) 原始振动信号频谱 图8 原始信号与频谱

(a) 重采样振动信号

(b) 阶次谱 图9 重采样信号与阶次谱
图10分别为振动信号三维频谱图和三维阶次谱图,信号特征在此图中反应更加清晰。在图中都有且只有一条阶次为40阶的亮线。从三维频谱图中可以观察到设备的几个固有频率,分别为310、500、730、950和1750Hz。从三维阶次谱图中可以观察到,此条阶次线能量从300r/min时出现,700r/min时增强,1600r/min时突然消失,2000r/min处再次出现并有增强趋势。峰值出现在1400r/min和1050r/min处。因为此时该阶次与设备固有频率730Hz和950Hz重合,发生耦合共振现象,致使振动幅值叠加增强。仔细观察图像,其倍频10阶20阶与80阶处也出现亮线,不排除此特征阶次是由轴承缺陷所致。故提出以下优化建议:在结构方面,更换主轴轴承;在加工工艺方面,加工时主轴转速应选1600r/min到2000r/min之间,避开各个振动峰值所对应的主轴转速。

(a) 三维频谱图

(b) 三维阶次谱图 图10 三维频谱图与三维阶次谱图
4 结论
通过引入Vold-Kalman滤波阶次分析方法,有效提高阶次谱图分辨率;并在算法中采用流水线技术实现并行处理,克服Vold-Kalman滤波阶次提取时大量矩阵运算耗时长的不足。仿真信号分析结果表明,所述方法在提高分辨率和提取密集阶次与交叉阶次时的优越性;实际应用中该系统结果准确性能优良,为设备状态监控与故障诊断提供技术及软件支持。

