一种基于改进阶次包络谱的滚动轴承故障诊断算法
郝高岩, 刘永强, 廖英英
(石家庄铁道大学 机械工程学院,石家庄 050043)
一种基于改进阶次包络谱的滚动轴承故障诊断算法
郝高岩, 刘永强, 廖英英
(石家庄铁道大学 机械工程学院,石家庄050043)
针对变转速工况下滚动轴承故障特征的提取问题,提出了一种基于滤波定阶理论的改进阶次包络谱分析方法。该方法在包络解调后,先对信号进行低通滤波,在确定计算阶次跟踪(COT)的重采样频率并进行重采样后,再对重采样后的包络曲线进行离散傅里叶变换得到阶次包络谱。通过仿真信号和实验数据对该算法进行验证,结果表明:该算法适用于变转速工况的轴承故障诊断,和传统阶次包络谱算法相比,该算法为角域重采样中重采样率的设置提供了一种方法,可以有效避免阶次混叠现象和降低重采样率。
非平稳;阶次包络谱;重采样;阶次混叠
滚动轴承是旋转机械设备中应用最广泛的机械零件之一,同时也是最容易损坏的零件之一,尤其是在载荷比较大,转速变化剧烈的启停阶段更易损坏。因此,针对非平稳工况下轴承故障诊断算法的研究具有重要的实际意义。
当轴承内圈、外圈、保持架或滚子出现局部损伤时,会出现周期性的冲击,这些冲击会对轴承系统固有振动(或其他固有振动,如传感器谐振)信号形成调制,冲击出现的频率(调制频率)为内圈、外圈等的通过频率[1],因此可以通过包络解调的方法提取出轴承故障特征频率。
在转速变化工况下,轴承振动信号为非平稳信号,并不直接满足傅立叶变换对信号的平稳性要求,若人为将这类信号假定为平稳信号进行处理,结果将产生严重的“频率模糊”现象[2-3]。针对这一问题,可以利用样条插值算法进行角域重采样得到等角度分布的采样点,将时域中的非平稳信号转换为角域平稳信号,再进行傅里叶变换得到阶次谱,即利用阶次跟踪算法[4]来避免出现“频率模糊”现象。应用效果显示了阶次跟踪分析法在变转速工况下轴承故障诊断的优越性。
1 传统RE-SES阶次包络谱算法
Borghesani等[5]在阶次包络谱算法的基础上提出了RE-SES(Reversed Sequence Squared Envelope Spectrum)算法,算法流程如图1所示。
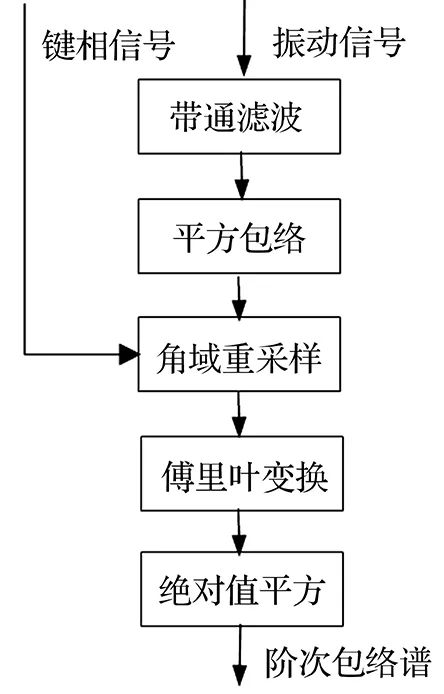
图1 RE-SES算法流程图Fig.1 RE-SES algorithm procedure
RE-SES算法中先对时域信号带通滤波,通常选取传感器的谐振频率作为中心频率,提取富含故障信息的高频成分,再对滤波信号包络解调并对包络信号重采样,最后对重采样包络信号傅里叶变换得包络阶次谱,提取轴承故障特征。由于对时域信号进行带通滤波,滤波的中心频率和带宽易选取,因此RE-SES算法可以适用于转速任意变化的工况[5]。
(2) RE-SES算法虽然可以适用于转速任意变化的工况,但对重采样率的计算没有做出明确的说明,只能通过经验进行设定,在重采样环节易产生阶次混叠现象。要想避免产生阶次混叠,需要大幅提高重采样率,势必会造成数据处理量的增加,但实际中我们无法准确得知其阶次成分,即使采用了大的重采样率,也无法完全避免阶次混叠问题。本文对此进行改进,提出基于低通滤波定阶理论的改进阶次包络谱算法。
2 角域重采样定理和滤波定阶理论
角域重采样中, 存在与时域采样定理(即 Nyquist 定理)相似的角域采样定理[6]:角域采样率需至少是信号最高分析阶次的两倍,即
Os≥2×Omax
(1)
式中:Os为阶次采样率(即每转内等角度采样点数),Omax为最大分析阶次。
低通滤波定阶理论[7-8]:首先根据信号需要分析的最高阶次和最高转速,确定低通滤波的截止频率fc,然后根据低通滤波截止频率和最低转速确定重采样率。设某信号为随转速变化的信号,时域采样频率为fs,参考轴的最高转速为nmaxr/min,最低转速nminr/min,信号最高分析阶次为Omax。则低通滤波的截止频率
在反复操练后,学生也就很自然得出以下结论:虚拟语气还可以用来表达与将来几乎不可能实现的情形等,并且学生很容易完成下表:
fc=nmax×Omax/60
(2)
滤波后信号包含的最高阶次
Omax=60×fc/nmin
(3)
由角域采样定理得,角域重采样频率
Os≥2×Omax
(4)
由式(2)可以得出信号的最高频率和最大阶次关系:
fmax=Omax×nmax/60
(5)
3 基于滤波定阶理论的改进RE-SES算法
Borghesani等提出的传统RE-SES算法中对包络信号直接重采样,为了避免阶次混叠,通常采用大的重采样率,如果信号中包含了远远大于故障特征阶次的成分,那么重采样率要很大。并且在实际中我们无法准确得知其最高的阶次成分,肯定会发生阶次混叠问题。文中提出改进RE-SES算法,算法中通过低通滤波可以将待分析信号的阶次限定在一定范围,只分析我们感兴趣的成分,即预分析的阶次范围。计算滤波后的最高阶次,根据最高阶次设定重采样率,再进行角域重采样,就可完全避免阶次混叠。改进算法的流程图如图2所示。
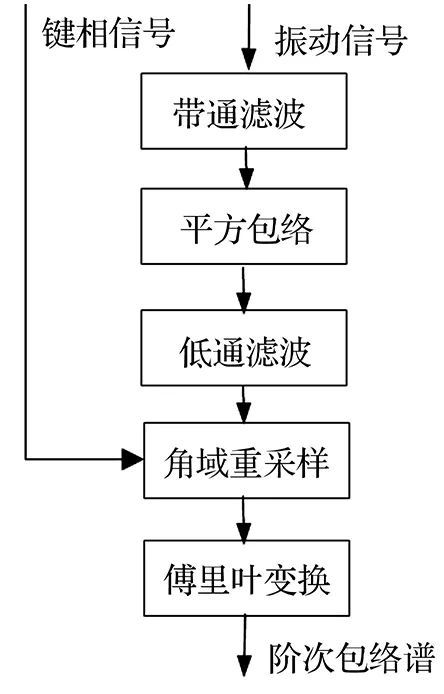
图2 基于低通滤波定阶的RE-SES算法Fig.2 RE-SES algorithm based on low pass filter limiting the maximal order
4 仿真信号验证
下面通过仿真信号对比传统RE-SES算法和改进RE-SES算法。
这里采用仿真信号
x(t)=sin(9πt2/8+2πt)+
0.5×sin[2×(9πt2/8+2πt)]+
0.75×sin[40×(9πt2/8+2πt)]
将sin(9πt2/8+2πt)作为阶次为1的参考轴信号,计算得到转速键相信号,仿真信号如图3所示,键相信号如图4所示,仿真信号频率随时间线性增加。转速曲线如图5所示,转速从148 r/min线性增加到580 r/min。
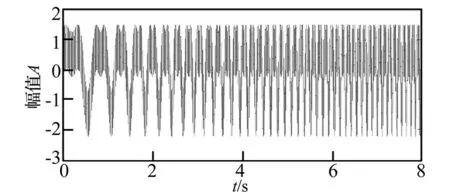
图3 时域仿真信号Fig.3 Simulating signal in time domain
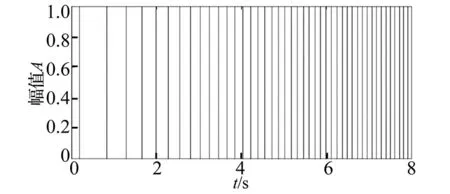
图4 键相信号Fig.4 Impulse train in time domain
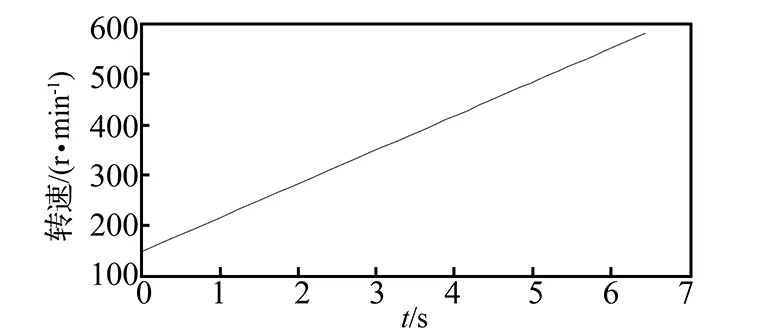
图5 转速曲线Fig.5 Speed profile in time domain
仿真信号中包含1、2、40阶次成分,采用传统RE-SES算法,这里的1、2阶次是我们感兴趣的成分,由式(1)可知,我们取重采样频率Os=8,得到的阶次谱如图6所示。图中在阶次为8处出现明显峰值,但原始仿真信号中并没有该阶次成分。分析原因,是因为我们采用的重采样频率对于1、2阶次成分满足重采样定理,但对于40阶次成分不满足,所以出现了阶次混叠现象。
在实际轴承故障诊断中,包络信号的阶次成分并不清楚,就如仿真信号中的40阶次成分,如果包络信号中包含了高于重采样频率一半的阶次成分,就会出现阶次混叠,影响诊断效果。
采用改进RE-SES算法,对信号进行低通滤波,将40阶次成分通过滤波去除。
由式(2)可知,低通滤波的截止频率fc=2×580/60=19.3。取fc=20。
由式(4)可知,重采样率Os≥120×20/148=16.2。取Os=20。
改进算法的阶次谱如图7所示,信号中本没有的阶次为8的分量消失了,避免了阶次混叠现象。
如果采用传统RE-SES算法,因为信号中最高阶次为40,要避免阶次混叠,重采样率至少为80,而改进RE-SES算法的重采样率为20,要低得多。这里采用传统算法,取Os=120,阶次谱如图8所示。从这个角度分析,采用低通滤波可以降低重采样频率。
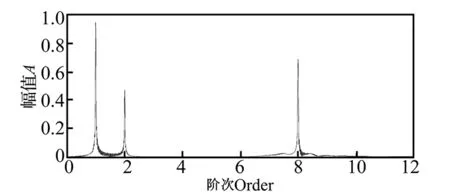
图6 传统RE-SES算法阶次谱,Os=8,出现阶次混叠现象Fig.6 Traditional RE-SES algorithm order spectrum,Os=8,arising order aliasing phenomenon
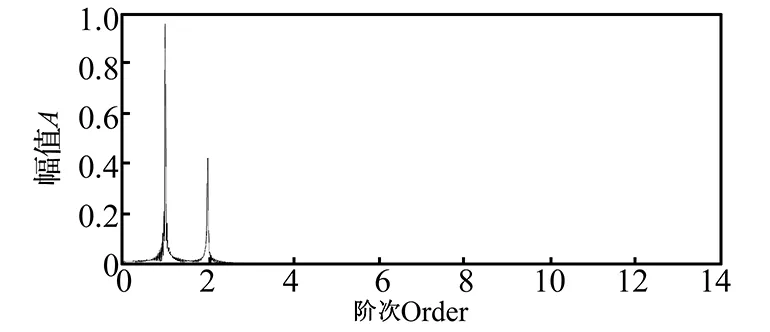
图7 改进RE-SES算法阶次谱,Os=20,避免阶次混叠,降低重采样率Fig.7 Improved RE-SES algorithm order spectrum,Os=20 avoiding order aliasing and reducing resample frequency
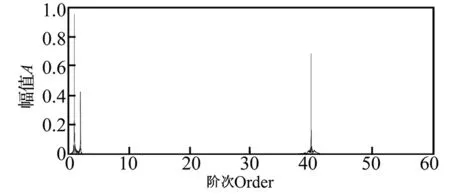
图8 传统RE-SES算法阶次谱,Os=120Fig.8 Traditional RE-SES algorithm order spectrum,Os=120
5 实验信号验证
为了对比传统方法与改进算法在实际轴承故障诊断中的效果,对实际采集的轴承信号进行阶次包络谱分析。实验中采用的设备是旋转机械振动及故障模拟试验台QPZZ-Ⅱ系统,如图9所示,1为CA-YD-188型振动加速度传感器,2为激光转速计。实验对象为具有轻微外圈裂纹故障滚动轴承,轴承内滚道直径d1=25 mm,外滚道直径D1=52 mm,滚子直径d=7.2 mm,滚子个数Z=13,接触角α=0。模拟制动时的工况,转速曲线如图10所示,速度从1 175 r/min下降到233 r/min,轴承时域振动信号如图11所示。
轴承故障特征频率计算公式
内圈fbpfi=Zfi[1+d/D×cos(α)]/2
外圈fbpfo=Zfi[1-d/D×cos(α)]/2
保持架fc=fi(1-d/D×cos(α))/2
滚子fbsf=fiD{1-[d/D×cos(α)]2}/(2d)
式中:D=(d1+D1)/2。
则外圈轴承故障特征阶次为Obpo=Z[1-d/D×cos(α)]/2=5.28。

图9 旋转机械振动及故障模拟试验台Fig.9 Rotating machinery vibration and fault test-rig
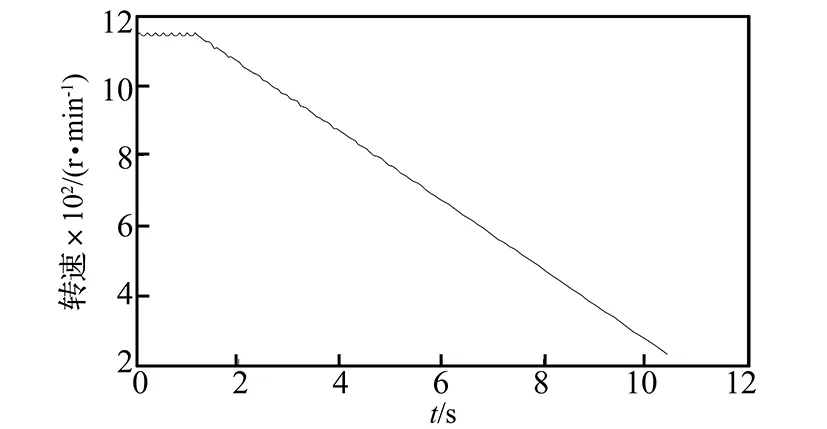
图10 减速工况下的转速曲线Fig.10 Speed profile in decelerating mode
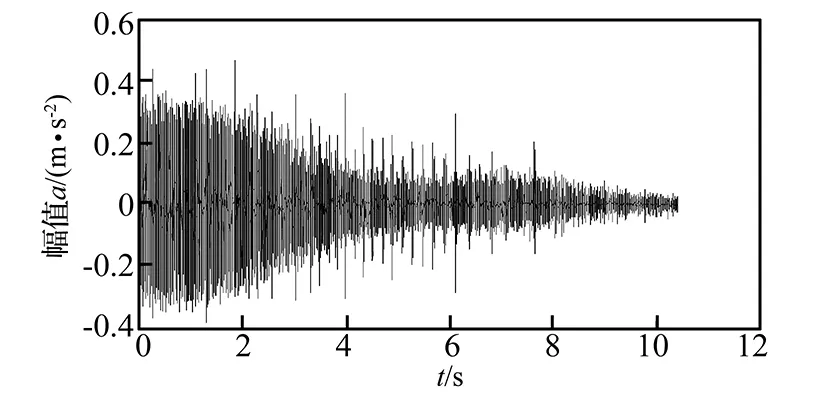
图11 减速工况下的轴承时域振动信号Fig.11 Bearing vibration signal in decelerating mode
采用传统RE-SES算法,选取带通滤波的中心频率fk=8 300 Hz(压电加速度传感器的谐振频率),带宽fb=2 000 Hz。根据信号中预分析的阶次范围(阶次选择为轴承外圈故障特征阶次5.28)和重采样定理,取重采样率Os=12,所得包络阶次谱如图12所示。从图中可以看出,除了轴承外圈故障特征阶次一倍频5.24处的峰值外,在1.5、3、3.7阶也存在明显峰值。
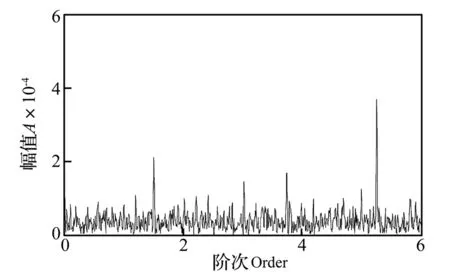
图12 减速工况下传统RE-SES算法阶次包络谱,Os=12Fig.12 Traditional RE-SES algorithm order spectrum,Os=12
采用改进RE-SES算法,平方包络后低通滤波,预分析阶次Omax=5.28,这里取Omax=6,低通滤波器的截止频率按式(2)计算得fc≥6×1175/60=117.5 Hz,取fc=118 Hz,则角域重采样率Os≥2×fc/(nmin/60)=60.7,取Os=60。得到的阶次包络谱如图13所示。从图中可以清晰看出,轴承外圈故障特征阶次处峰值明显,1.5、3、3.7处的峰值消失,避免了阶次混叠现象对诊断结果的影响。
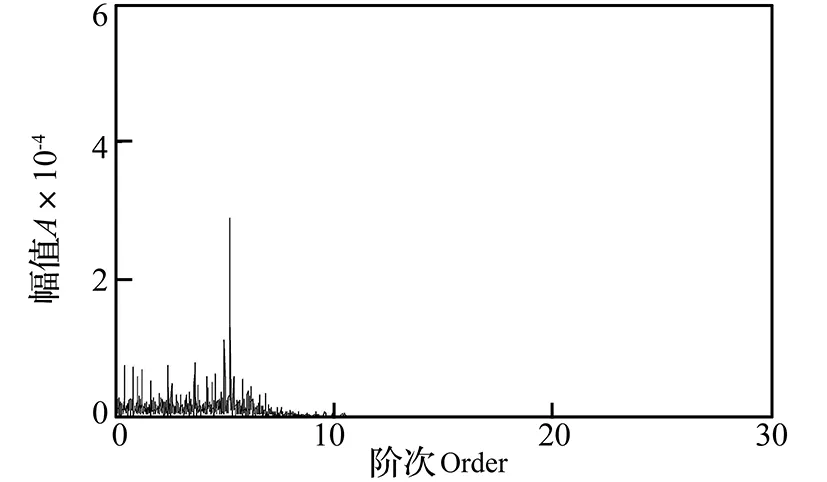
图13 减速工况下改进RE-SES阶次包络谱,Os=60Fig.13 Improved RE-SES algorithm order spectrum,Os=60
这里说明一下,在重采样率Os=12时出现的1.5、3、3.7的阶次成分是由5.24的二倍频10.5、三倍频15.8及更高阶次成分发生阶次混叠而产生的。
我们预分析的阶次为5.28,高于该阶次的成分被滤波器滤除了,图13中没有出现其他倍频成分。如果想分析其他倍频峰值,只需增大预分析阶次范围即可。增加预分析阶次范围,取五倍频为最高分析阶次,由式(5)可知,信号的最高频率fmax=5×5.24×(nmax/60)=513 Hz,由式(3)可知信号中隐含的最高阶次Omax=fmax/(nmin/60)=132,要避免发生阶次混叠现象,这里的重采样率取270,得到的改进阶次包络谱如图14所示,轴承故障特征阶次的1-5倍频峰值均出现。
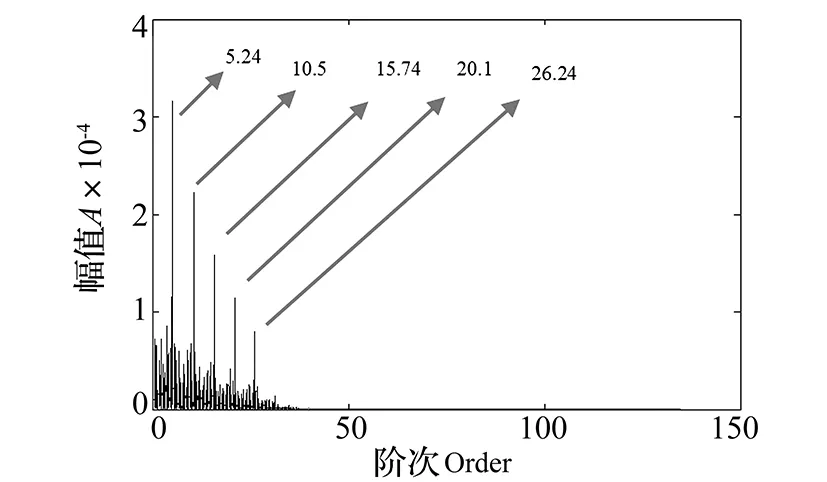
图14 减速工况下改进RE-SES阶次包络谱,Os=270Fig.14 Improved RE-SES algorithm order spectrum,Os=270
6 结 论
RE-SES算法在变转速工况的滚动轴承故障诊断中发挥着重要作用,传统的RE-SES算法对平方包络信号直接进行角域重采样,但实际的包络信号阶次成分我们无法得知,如果重采样频率不够大就会发生阶次混叠,相反,为了避免阶次混叠就需要很高的重采样率,这样重采样后的数据量会很大。本文提出的基于低通滤波定阶的改进RE-SES算法,对解调后的包络信号进行低通滤波,确定滤波后的最大阶次,再进行角域重采样,既降低了重采样频率又避免了阶次混叠现象。通过仿真信号和实验信号验证,此改进RE-SES算法具有很好的应用前景。
[1] Kiral Z,Karagulle H.Simulation and analysis of vibration signals generated by rolling element bearing with defects[J]. Tribology International, 2003,36: 667-678.
[2] 康海英,栾军英,田燕,等. 阶次跟踪在齿轮磨损中的应用[J]. 振动与冲击,2006,25(4):112-113.
KANG Hai-ying,LUAN Jun-ying,TIAN Yan,et al. Application of order tracking in wearing gear[J].Journal of Vibration and Shock, 2006,25(4): 112-113.
[3] 朱继梅. 非稳态振动信号分析(连载)[J]. 振动与冲击,2000,19(2):87-90.
ZHU Ji-mei.Analysis for non-stationary vibration signal(serial)[J].Journal of Vibration and Shock, 2000,19(2): 87-90.
[4] Fyfe K R, Munck E D S. Analysis of computed order tracking[J]. Mechanical Systems and Signal Processing,1997,11(2):187-205.
[5] Borghesanin P, Ricci R, Chatterton S, et al.A new procedure for using envelope analysis for rolling element bearing diagnostics in variable operating conditions[J]. Mechanical Systems and Signal Processing, 2013,38:23-35.
[6] 戴功伟. 基于自适应转频跟踪滤波的旋转机械阶次分析研究[D]. 重庆:重庆大学,2013.
[7] 丛华,吴广平,饶国强,等.计算阶次分析中避免阶次混叠的滤波定阶方法及其应用[J].振动与冲击,2012,31(12):42-44.
CONG Hua,WU Guang-ping,RAO Guo-qiang,et al.A method to avoid order aliasing in COT based on filtering[J]. Journal of Vibration and Shock, 2012,31(12): 42-44.
[8] 汪伟,杨通强,王红,等.非稳态信号计算阶次分析中重采样率研究[J]. 振动、测试与诊断,2009,29(3):349-351.
WANG Wei,YANG Tong-qiang,WANG Hong,et al.Research on resampling of order tracking analysis of non-stationary signals[J].Journal of Vibration,Measurement & Diagnosis, 2009,29(3): 349-351.
A rolling bearing fault diagnosis algorithm based on improved order envelope spectrum
HAO Gaoyan, LIU Yongqiang, LIAO Yingying
(Department of Mechanical Engineering, Shijiazhuang Railway University, Shijiazhuang 050043, China)
To extract fault characteristics of rolling bearings under variable speed conditions, an improved order envelope spectrum algorithm was proposed based on the method to use low-pass filter to limit frequency and order. The envelope signals were obtained after the original vibration signals were filtered with a low-pass filter, then the re-sampling frequency of COT(computed order tracking) was determined and the filtered envelope signals were re-sampled. Finally, the improved order envelope spectrum was obtained using the absolute values of the discrete Fourier transformation of the re-sampled envelope signals. The results showed that the proposed algorithm provides a method to evaluate the re-sampling rate, the method reduces the re-sampling rate and avoids the order aliasing compared with the traditional order envelope spectrum algorithm.
non-stationary; order envelope spectrum; re-sampling; order aliasing
国家自然科学基金(11227201;11202141;11302137;11472179);河北省自然科学基金(A2013210013;A2015210005);河北省教育厅项目(YQ2014028)
2015-05-25修改稿收到日期:2015-07-24
郝高岩 男,硕士生,1988年2月生
刘永强 男,博士,副教授,1983年12月
TH165.3
A
10.13465/j.cnki.jvs.2016.15.024

