随机激励下风机齿轮箱动力学建模及故障特征提取
何 俊, 杨世锡, 甘春标
(浙江大学 机械工程学院, 杭州 310027)
随机激励下风机齿轮箱动力学建模及故障特征提取
何俊, 杨世锡, 甘春标
(浙江大学 机械工程学院, 杭州310027)
研究随机激励下的风机齿轮箱动力学特性,同时对典型的早期局部齿形故障特征进行提取。首先,建立了具有十六个自由度的风机齿轮箱动力学模型,模拟了多组随机不确定风载数据并作用在模型上进行仿真计算,通过分析内部齿轮振动信号的时频谱图和概率密度函数,研究随机不确定风载对齿轮箱动力学特性的影响。其次,在模型中考虑不同程度的齿面缺陷故障,运用同步小波压缩方法对仿真计算得到的齿轮振动信号进行分析。研究结果为分析不同工况下的风机齿轮箱动力学特性提供参考。
风机齿轮箱;随机激励;动力学建模;同步小波压缩;故障特征提取
齿轮箱是风机系统的关键部件,它的正常运行通常会受到系统的动力输入部件及负载部件的影响。同时,随机不确定风载,时变啮合刚度以及一些常见的故障模式,均会导致齿轮箱的动力学特性非常复杂。因此,对受随机激励下的风机齿轮箱结构进行动力学特性研究以及故障特征提取显得尤为重要。
目前,已有一些学者针对简单的齿轮箱动力学模型进行研究,如Bartelum[1]建立了一级传动齿轮箱动力学模型,加入一随机误差模型用于研究齿轮箱在设计、制造及运行过程中产生的一系列偏差对动力学特性的影响。Parey[2]建立了包含局部齿形故障的二级传动齿轮箱动力学模型,采用正弦衰减脉冲来模拟模型中的点蚀、断齿等故障,同时利用基于EMD的统计分析方法对多种不同程度的故障进行了区分。此外,为了提高模型的准确性,众多学者在建模的过程中做出了更多的尝试,如增加模型的自由度、引入时变啮合刚度、考虑实际运行工况中出现的多种非线性因素等等[3]。上述众多研究成果均是利用确定性理论来解决齿轮箱的问题,因此在处理由随机激励引起的齿轮箱动力学问题时便具有很大的局限性。如今已有一些学者开始重点考虑随机负载对齿轮箱系统的影响。Tobe[4]最先通过实验证明了齿轮传递误差中存在随机因素,之后他建立了含有随机微分方程的齿轮箱动力学模型并利用统计线性化方法进行求解。Wen[5]在建立的齿轮箱动力学模型当中同时加入了确定负载和随机负载,此外还考虑了齿间侧隙和时变啮合刚度等非线性因素,运用路径积分方法获取系统随机响应的概率密度分布。
风力发电机通常工作在环境较为恶劣的地区,风速的急剧变化会产生随机不确定风载作用于风机系统上。齿轮箱作为关键传动机构也必然会经常受到随机激励。此外,风机的动力输入机构以及负载机构也会对齿轮箱的正常运行产生影响,再加上时变啮合刚度,局部齿故障等因素,齿轮箱的振动响应通常极为复杂。然而,现如今大部分研究工作往往将齿轮箱从整个机械设备中剥离开来单独研究,考虑随机激励的则更是少之又少,因此具有很大的局限性。
本文针对上述问题,同时考虑实验室环境下模拟试验的局限性,对风机齿轮箱机构进行了一定的简化与改造并建立模型,旨在研究外部随机激励和常见故障模式对齿轮箱系统动力学特性的影响,具体章节安排为:引言部分简短地介绍了齿轮箱动力学研究的进展,提出本文的研究内容;第一节介绍了本文建立的系统动力学模型以及随机激励模型;第二节在建立的模型的基础上进行实例分析,研究不同工况下的齿轮箱动力学特性并进行对比分析;第三节为本文的结论。
1 系统动力学模型
为了充分研究齿轮箱的动力学特性,众多学者分别提出了多种动力学模型。早期的许多动力学模型只考虑一对齿轮啮合的情况,或者将齿轮箱简化为线性时不变系统[6]。而如今一些学者在增加模型自由度的同时,还考虑了系统中存在的某些非线性时变因素,如齿间侧隙,时变啮合刚度等等[3]。在几位学者提出的二级传动齿轮箱动力学模型的基础上,本文建立的模型结合风机齿轮箱的实际运行工况,加入了随机不确定风载、时变啮合刚度、齿故障等非线性特征。

图1 齿轮箱系统动力学模型Fig.1 The dynamics model of gearbox system
实际的风机齿轮箱动力来源于风机主轴,之后经过多级啮合齿轮加速带动后端的发电机工作。不过在实验室环境下较难模拟风能带动风机主轴低速旋转这一过程,因此通常的替代方法是用电动机带动齿轮箱的高速轴以发电机的额定转速旋转,而低速轴输出端则连接一简化的叶轮机构或圆盘,这样同样能再现风机齿轮箱的工作状况,同时尽可能地复现风机叶轮的悬臂结构。本文在建立模型时同样考虑了实验室环境下模拟试验的局限性,对风机齿轮箱机构进行了一定的简化与改造。图1即为本文所建立的风机齿轮箱系统动力学模型,此模型包括两对啮合齿轮,电机输入轴,齿轮箱输出轴以及外接圆盘。其中,mj(j=1,2,3,4,5)为四个齿轮和圆盘的质量,Ij(j=0,1,2,3,4,5)为电机输入端、四个齿轮和圆盘的转动惯量,T1为齿轮箱输入转矩,T2为齿轮箱输出转矩。每一个齿轮基座的约束均简化为水平和竖直方向的弹性连接,两方向的约束刚度和阻尼分别为Kf和Cf。此外,一号齿轮受到电机输入轴的扭转刚度Kn、阻尼Cn的约束;二号和三号齿轮受到齿轮轴的扭转刚度Kg、阻尼Cg的约束;四号齿轮受到齿轮箱输出轴的扭转刚度Kt、阻尼Ct的约束,同时在水平和竖直方向,还需考虑外接圆盘主轴的弯曲刚度Ks、阻尼Cs的影响。α为齿轮压力角。
由牛顿第二定律,得到如下运动微分方程:
(1a)
(1b)
(1c)
(1d)
(1e)
(1f)
(1g)
(1h)
(1i)
(1j)
(1k)
(1l)
+Ks(x4-x5)=-F34(t)sinα
(1m)
Ks(y4-y5)=-F34(t)cosα
(1n)
(1o)
(1p)
式中:齿间啮合力F12(t)和F34(t)分别为:
(2a)
(2b)
式中:Kz为齿间啮合刚度,Cz为啮合阻尼,δ12和δ34为啮合齿轮之间的相对位移,它们可分别表示为:
δ12=(x1-x2)sinα+(y1-y2)cosα+r1φ1-r2φ2(3a)
δ34=(x3-x4)sinα+(y3-y4)cosα+r3φ3-r4φ4(3b)
齿轮在啮合过程中基本上都存在单齿啮合和双齿啮合交替出现的状况,这种啮合方式会导致啮合刚度也在随时波动。Wang、Howard[7]等学者利用有限元方法对啮合刚度的时变情况进行了细致的研究。根据他们的研究成果,齿轮啮合刚度可以近似地表示成一方波函数:
n=1,2,3…
(4)
式中:K1,K2为两种不同的啮合刚度值,Tm为齿轮的啮合周期,Th表示啮合刚度为K1时的时间区域。
对以上确定性情形,即忽略齿轮箱系统中普遍存在的随机不确定成分,众多学者在动力学建模及数值分析方面已经有了较为透彻的研究[3]。然而,在实际运行工况下,风场随机风速的大小和动态变化会对风电齿轮箱的工作性能和可靠性产生重要影响。因此,为了更准确地研究风力发电机齿轮传动系统的动力学特性,必须建立与实际风速相符合的风速模型,在模拟真实风速变化的情况下研究风力发电机齿轮传动系统的动态性能和可靠性。 近年来一些学者已对随机风速模型进行了大量的研究,并取得一定的成果,例如:Davenport风速模型[8],双参数Weibull分布的风速模型[9]等。本文采用的是Davenport风速模型。风速功率谱经验公式如下:
(5)
式中:f为角频率,a为风速标准差,v(n)是代表离地高度n米处的平均风速。
由Shinozuka[10]的谐波叠加法可产生脉动风速的一个充分遍历的样本。假设脉动风速是一个零均值平稳高斯过程,其单边功率谱密度函数为S(n),有

(6)
式中:Δn=(nu-nl)/N,nk=nl+(k-0.5)Δn,nu、nl分别为S(n)的上限频率和下限频率。φk为随机相位角,它服从[0,2π]上的均匀分布。
在大部分的气动模型中,通常都假定在给定径向位置处的流动是二维的,即叶片只受到水平和竖直两方向的力,即图2中的升力L和阻力D。此外,风载还将产生导致叶片旋转的风力矩M。升力L、阻力D和力矩M的计算方法如式(7a),(7b),(7c)所示:
(7a)
(7b)
(7c)
式中:Cl为升力系数,Cd为升力系数,Cm为升力系数,ρ为风速,ν为风速,A为风轮扫琼面积。

图2 叶片受力简图Fig.2 The force diagram of blade
考虑了随机激励之后,本文模型中的外接圆盘还将受到一随机力矩M(t),水平方向随机力D(t)以及竖直方向随机力L(t)。这些随机成分的具体数值可根据风速的实时变化情况求得。
2 系统动力学特性与信号特征分析
在上文提出的动力学模型的基础上,本文将首先研究不受随机激励的健康齿轮箱动力学特性,分析齿轮箱在不同转速下的振动信号。之后再研究随机激励下齿轮箱动力学特性的变化,最后在模型中加入故障因素并进行特征提取。
本文选取的大部分模型参数来自于实验室自主搭建的实验平台。其他一些不便测量的参数则参考比较各类文献资料,选取与本文所建模型较为贴近的文献中的数据。其中,模型采用的是渐开线直齿圆柱齿轮,其他主要的参数见表1。

表1 齿轮箱主要参数
此外,随机风载模型的相关参数选择与翼型的种类有较大的关系。本文参考空气动力学的相关资料,选取FX67-K-170翼型的参数用于本模型的研究工作。其他一些主要的参数如下所示:
m5=3.2 kg;p=1.23 kg/m3;
Cl=1;Cd=0.02;Cm=0.35;
Kn=Kt=1 917 N·m/rad;Kg=3 383 N·m/rad;
Cm=Ct=0.27 N·m·s/rad;Cg=0.26 N·m·s/rad;
Kf=107 N/m;Cf=1 000 N·s/m;
f=100π;a=5;Lv=1 200,v=20 m/s
2.1无随机激励时健康齿轮箱的动力学特性


图3 不同转速下齿轮速度信号的频谱图Fig.3 The spectrum of gearvelocity signal under different rotation speed

图4 不同转速下齿轮振动信号的相图Fig.4 The phase diagram of gearvibration signal under different rotation speed
图3和图4为齿轮箱高速轴转速分别为1 000 r/min和3 000 r/min时第四个齿轮的速度信号频谱图以及相图。转速的变化主要会导致各级齿轮的啮合频率改变,齿轮在变化的受力情况下进而会产生不同的动力学现象。从频谱图中可以发现,速度信号的频率成分主要为齿轮啮合频率及其倍频。当转速为1 000 r/min时,有多个频率成分幅值较大,因此可以把该转速下的速度信号描述成多个不同周期成分相叠加,相图也说明此时系统呈现的是多周期运动。而当转速为3 000 r/min时,速度信号的频率成分虽然也包含齿轮啮合频率及其倍频,但相比起啮合频率, 倍频成分的幅值十分微弱。因此可以把该转速下的速度信号描述成单周期成分加上一些能量十分微弱的其他周期成分,相图也说明该工况下系统呈现的是典型的单周期运动。
为了充分研究齿轮箱的动力学特性,本文还采用时频分析方法对振动信号进行对比分析,具体内容如下文所见。
2.2随机激励下健康齿轮箱的动力学特性与信号特征
本节将采用上文所述的Davenport风速模型和谐波叠加法模拟多组随机不确定风载数据,分别把它们作用在模型上进行仿真计算,之后通过分析内部齿轮振动信号的时频谱图和概率密度函数,研究随机不确定风载对齿轮箱动力学特性的影响。
随机不确定风载会对齿轮箱输入轴产生一随机变化的驱动力矩,进而改变各级齿轮的转频以及啮合频率。因此,当受到随机不确定风载作用时,式(4)中的Tm和Th都不再恒定。啮合频率、升力和阻力的随机变化都会对齿轮箱的动力学特性产生影响。同时,与确定性激励不同,随机激励的特点在于它在时域上无法准确预测。因此它对系统的影响不能仅仅通过对一段有限长度的数据进行分析来描述。以往已有一些学者采用统计学的相关方法对动力学系统中存在的随机因素进行分析并取得一定的成果[5]。本文共模拟了32组随机不确定风载数据并作用在模型上进行仿真计算,之后分析第四个齿轮振动信号概率密度函数,研究齿轮箱在随机激励下的振动模式。其中,32组风载数据的平均风速为20 m/s。
图5显示了一个周期内齿轮竖直方向速度信号的概率密度函数变化情况。四幅图分别表示一个周期内四个相等间隔时间点的数据。从图中我们可以发现,在随机激励下齿轮速度具有不确定性。我们可以通过概率密度函数来预测齿轮速度的范围及各点取值的概率,但无法准确地计算出具体数值。同时,任一时刻速度的概率密度函数也不相同,因此无法像受确定性激励的情况一样可以根据以往数据准确地预测将来数据。齿轮位移的概率密度函数与速度的情况类似,这里便不再详细说明。

图5 不同时刻齿轮速度信号的概率密度函数Fig.5 The probability density function of gearvelocity signal in different moments
此外,随机激励下齿轮箱的振动信号还具有强烈的非平稳性。因此,一些传统的频谱分析方法显然无法有效地提取出复杂信号的瞬时特征。近年来一些学者在这一领域进行了大量的研究,并提出了多种信号处理新方法。Xiong[11]针对谱峭度(SK)对非平稳信号的敏感性,提出了一种基于SK-HHT的新方法。Daubechies[12]提出了一种同步小波压缩算法,该方法以小波变换为基础,首先对任意信号进行连续小波变换,进而建立起信号瞬时频率与尺度因子和平移因子之间的映射关系,之后再在小波尺度方向上对时间-尺度平面的能量进行重新分配并将其转换为时间-频率平面,其离散计算式为:
Tx(ωl,b)=
(8)

相比起传统的小波分析方法,该方法可以提高时频聚集性,消除干扰项,从而能进一步洞察非平稳信号内部组成成分。本文即采用同步小波压缩算法对第四个齿轮的竖直方向速度信号进行时频谱分析。齿轮箱高速轴的转速设为1 000 r/min。
图6(a)是不受随机激励时信号的时频谱图,由于信号低频域段成分能量十分微弱,所以本文只截取了频率范围为50 Hz到500 Hz这一段进行重点分析。从图中我们可以发现信号的主要成分为齿轮的啮合频率及其倍频。其中能量主要集中在中频域段,即频率范围为50 Hz到200 Hz。而在高频域段,能量逐渐衰减,同时在啮合频率的高倍频附近出现了调频现象,这导致了能量在整个高频域段内较为分散,而不像低频域段都集中在几个主要的频率成分。图6(b)是受随机激励时信号的时频谱图,频率范围为50 Hz到500 Hz。与图6(a)相比较,信号的主要成分同样为齿轮的啮合频率及其倍频,但是它们都出现了较严重的调频现象,瞬时频率随时间出现明显的波动,不再集中在几个固定的频率成分内。此外,在不同的时间点,信号的能量大小也会发生一定的变化。通过上述两种情况的对比我们可以发现,当不受随机激励时,健康齿轮箱的振动信号整体较为平稳,只有一小部分高频成分出现了调频现象,但由于这些成分能量较为微弱,因此并不会对齿轮箱的正常运行产生太大的影响。而当受到随机激励时,振动信号开始出现强烈的非平稳性,瞬时频率随时间波动明显,这主要是因为此时各级齿轮的转频以及啮合频率都发生改变,导致了齿轮受力不再具有准确的周期性。此外,由于随机激励的大小随时间变化不确定,因此也会导致信号的能量大小在不同的时间会发生一些改变。

图6 两种不同工况下齿轮振动信号的时频谱图Fig.6 The time-frequency spectrum of gear vibration signal under two different conditions
2.3故障齿轮箱的动力学特性与信号特征
本节对存在不同程度局部齿形故障的齿轮箱动力学模型进行数值仿真,并采用同步小波压缩算法对得到的信号进行时频谱分析。齿轮箱高速轴的转速设为1 000 r/min。
局部齿形故障对系统的影响与故障方式、故障程度、啮合齿的基本参数、运行状况等多种因素相关。已有一些学者在这一领域发表了大量的研究成果[2]。其中,长时间运行的齿轮容易形成有一定宽度和深度的缺陷,同时随着缺陷的加深最终极有可能形成缺齿或断齿故障。综合考虑相关文献和齿面缺陷故障的影响因素,本文采用式(9)来表示系统对此类故障的响应情况,并着重于研究其脉冲特性对系统的影响:
(9)

本模型中设定第四个齿轮存在一处故障齿。因此考虑齿故障后三、四两齿间的啮合力F34的表达式为:
(10)
式中,f为故障齿正面的缺陷宽度,Kh为齿接触面的赫兹刚度,它的表达式为:
Kh=πE/4(1-ν2)
(11)
式中,E为杨氏模量,ν为泊松比。
在数值仿真过程中,本文设定两种不同程度的故障齿,侧面的缺陷深度均为1 mm,而正面的缺陷宽度分别为10 mm和15 mm。
图7和图8为两种不同程度故障信号的时频谱图。与健康信号的时频谱图相对比,我们可以观察到故障信号的时频谱图在整个时域段内存在周期性的脉冲成分,并且大致集中在中高频域段,即120 Hz到500 Hz。同时随着故障程度的加深此脉冲成分的能量也相应地增加。当受到随机激励时,振动信号开始出现强烈的非平稳性,瞬时频率随时间波动明显,在整个频域段内显得较为分散,而不像不受随机激励的情况下主要集中在几个固定的频率成分内。具体到体现故障特征的信号成分,其能量大小在不同的时刻也会发生一些改变,在一些时间点显得较为突出,而在另一些时间点则容易被其他波动的频率成分所掩盖。这一情况与上文所述随机激励会导致信号的能量大小随时间发生改变的情况相一致。

图7 故障信号的时频谱图(f=10 mm)Fig.7 The time-frequency spectrum ofthe fault signals(f=10 mm)
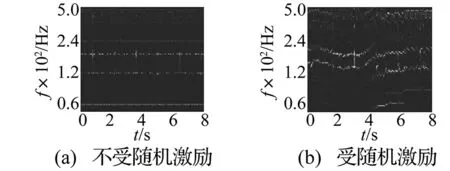
图8 故障信号的时频谱图(f=15 mm)Fig.8 The time-frequency spectrum of the fault signals(f=15 mm)
3 结 论
本文主要研究了随机激励下的风机齿轮箱动力学特性,同时对不同程度的局部齿形故障进行了分析,得到了如下结论:
(1) 当不受随机激励时,健康齿轮箱振动信号的频率成分主要包括齿轮啮合频率及其倍频,且随着转速的增加其倍频成分能量衰减明显,变得远小于基频成分。观察频谱图和相图也可以发现,随着转速的增加,系统响应由多周期成分叠加的运动逐渐转变为单周期运动。
(2) 在随机激励下,齿轮箱振动信号具有强烈的非平稳性。本文通过同步小波压缩算法对仿真得到的信号进行分析,并与不受随机激励下得到的信号进行对比。观察时频谱图可以发现,瞬时频率随时间波动明显,这主要是因为此时各级齿轮的转频以及啮合频率都发生改变,导致了齿轮受力不再具有准确的周期性。此外,由于随机激励的大小随时间变化不确定,因此也会导致信号的能量大小在不同的时间会发生一些改变。
(3) 在随机激励下,任一时刻齿轮的位移及速度具有不确定性。本文共模拟了32组随机不确定风载数据并作用在模型上,通过计算概率密度函数来预测它们的范围及各点取值的概率,但无法准确地计算出具体数值。
(4) 当齿轮箱存在一定程度的齿面缺陷时,可以从信号的时频谱图上观察到周期性的脉冲成分,该成分大致集中在中高频域段,且能量随着故障程度的加深而增大。随机激励会导致故障特征信号的频率和能量都发生不确定性变化,在一些时刻显得较为突出,而在另一些时刻则容易被掩盖,进而会对及时发现研究对象的故障特征带来一些不确定性。这一点也需要作者及其他学者做更深层次的研究。
[1] Bartelmus W. Mathematical modelling and computer simulations as an aid to gearbox diagnostics[J]. Mechanical Systems and Signal Processing,2001, 15(5): 855-871.
[2] Parey A, El Badaoui M, Guillet F, et al. Dynamic modelling of spur gear pair and application of empirical mode decomposition-based statistical analysis for early detection of localized tooth defect[J]. Journal of Sound and Vibration,2006, 294(3): 547-561.
[3] Wang J, Li R, Peng X. Survey of nonlinear vibration of gear transmission systems[J]. Applied Mechanics Reviews,2003, 56(3): 309-329.
[4] Tobe T, Sato K. Statistical analysis of dynamic loads on spur gear teeth[J]. Bulletin of JSME,1977, 20(145): 882-889.
[5] Wen Y, Yang J, Wang S. Random dynamics of a nonlinear spur gear pair in probabilistic domain[J]. Journal of Sound and Vibration,2014, 333(20): 5030-5041.
[6] Zg Ven H N, Houser D R. Dynamic analysis of high speed gears by using loaded static transmission error[J]. Journal of Sound and Vibration,1988, 125(1): 71-83.
[7] Wang J, Howard I. The torsional stiffness of involute spur gears[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,2004, 218(1): 131-142.
[8] Davenport A G. The spectrum of horizontal gustiness near the ground in high winds[J]. Quarterly Journal of the Royal Meteorological SocietyQ.J.R. Meteorol. Soc,1961, 87(372): 194-211.
[9] Seguro J V, Lambert T W. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis[J]. Journal of Wind Engineering and Industrial Aerodynamics,2000, 85(1): 75-84.
[10] Shinozuka M, Jan C M. Digital simulation of random processes and its applications[J]. Journal of Sound and Vibration,1972, 25(1): 111-128.
[11] Xiong X, Yang S, Gan C. A new procedure for extracting fault feature of multi-frequency signal from rotating machinery[J]. Mechanical Systems and Signal Processing,2012, 32(Sup1): 306-319.
[12] Daubechies I, Lu J, Wu H. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis,2011,30(2):243-261.
Dynamic modeling and fault feature extraction of a wind turbine gearbox under random excitation
HE Jun, YANG Shixi, GAN Chunbiao
(School of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China)
Here, the dynamic characteristics of a wind turbine gearbox under random excitation were investigated. Meanwhile, the characteristics of typical localized tooth defect were extracted. Firstly, a 16-DOF dynamic model under several groups of random uncertain wind load for the wind turbine gearbox was developed. The time-frequency spectrum and probability density function of internal gear vibration signals were analyzed to study the effects of random uncertain wind load on the gearbox dynamic characteristics. Then, different levels of localized tooth defect were considered, the synchrosqueezed wavelet method was used to analyze gear vibration signals obtained with numerical simulation. The study results provided a reference for analyzing dynamic characteristics of a wind turbine gearbox under different conditions.
wind turbine gearbox; random excitation; dynamic modeling; synchrosqueezed wavelet; fault feature extraction
国家自然科学基金资助项目(11172260;11372270;51375434);高等学校博士学科点专项科研基金资助项目(20110101110016)和浙江省科技计划项目基金资助项目(2013C31086)
2015-05-07修改稿收到日期:2015-07-22
何俊 男,博士生,1990年8月生
甘春标 男,教授,1971年生
E-mail: cb_gan@zju.edu.cn
TH113
A
10.13465/j.cnki.jvs.2016.15.006

