浅海目标回声测试及目标响应求解研究

何　呈， 赵安邦

(1. 哈尔滨工程大学 水声技术重点实验室， 哈尔滨　150001； 2. 哈尔滨工程大学 水声工程学院，哈尔滨　150001)



浅海目标回声测试及目标响应求解研究

何呈1,2， 赵安邦1,2

(1. 哈尔滨工程大学 水声技术重点实验室， 哈尔滨150001； 2. 哈尔滨工程大学 水声工程学院，哈尔滨150001)

使用液-固耦合振动模型对目标回声产生机理建模，推导耦合振动公式，得出单激励和多激励源下的目标回波表达式。从新的角度分析目标回波产生机制，并使用随机过程中的ARX模型构建目标模型。对于浅海环境中回波测试，使用多输入单输出ARX模型构建，最终分别求解出目标的直达入射波和在直达入射波作用下的直达回波，有效消除了多途信道的影响，获得了等效自由场中的测量结果。最后，通过水池实验验证了算法的有效性。

浅海信道；耦合振动；目标回波；ARX模型

为避免水声信道界面的影响，目标回波特性测试的理想环境是消声水池或深海。然而，由于水池尺寸的限制，大型目标在海中测试更为方便。中国的绝大部分海域为浅海，受浅海多途信道的影响，目标的入射波是发射信号的多途混叠，各个多途信号在时延、幅度、相位和角度上都不相同，不利于在测试中定量分析目标特性。受多途信道的影响，目标的回波是由目标在多途入射声信号作用下的多途回波构成，回波的成份复杂，无法测得仅在直达波入射条件下的直达目标回波。研究浅海环境下目标回声测试技术及消除浅海界面影响的方法，具有重要理论意义和实用价值。

Abraham等[1]研究了浅海环境下主动声纳探测目标的Page Test判决方法；Chen等[2]研究了多途环境下宽带波速形成算法，提高了图像声纳的清晰度；Xu等[3]研究了浅海环境下利用混响法探测目标方法；Sarkissian等[4]研究了浅海环境下目标响应提取算法；Harrison等[5]研究了脉冲声在多途信道影响下的信号包络形状。以上研究均是在浅海多途环境下尽可能提高设备所需功能的性能，未对各个子信道单独分析，并没有彻底消除多途信道的影响。目前，关于如何在浅海中估测目标的直达入射波及在直达入射波作用下的直达回波，去掉多途影响，并提取类似自由场中的测试数据，国内外鲜见对此深入研究的报道。

本文从新的角度，对目标回波产生机理、目标及多途对声能传输的影响进行了深入的分析并建模。首先，根据目标回波产生机理，结合机电类比和拉式变换，推导出目标在声激励下的表达式。在此基础上，提出了一种新的分析液-固耦合振动问题的方法，将液-固耦合问题模拟成随机过程中的ARX(Auto-Regressive with eXtra inputs)模型，将浅海环境下的多途作用模拟成多输入单输出的ARX模型，并巧妙的使用多途所产生的虚源作为系统的输入，据此可方便直观地分析各多途信号对目标入射声的作用，并解析出直达入射波和目标在直达入射波作用下的直达回波。最后，进行了水池实验，验证了算法的可行性和正确性。

1　目标回波建模

1.1两自由度耦合振动系统

实际中，目标不可能等效成完全的刚性体，入射声波对目标体的作用是水介质与目标体的耦合振动过程，因此，使用耦合振动对目标建模更符合实际的物理作用机制。如图1所示，为两自由度耦合振动系统。

图1两个自由度机械耦合系统
Fig.1 A mechanical coupling system of two degrees freedom

图1中，D表示弹性元件，m表示质量元件，R表示机械阻，F表示驱动力。图中所示有两个振子，(m1,D01)，(m2,D02)。其中(m1,D01)可认为是推动系统，为水介质；(m2,D02)相当于被激励系统，为水下目标(球体、圆柱体等)。耦合元件为弹性元件D12，其作用表现为机械作用(力)的耦合，称为机械耦合[6]。F1为介质中的声压的作用(如入射声波)，F2为目标体内部的激励源(如发动机的作用力)。图1的类比电路如图2所示。

图2　机电类比电路Fig.2 Electromechanical analogy circuits

将图2中的电路简化为如图3所示的四端口网络。

图3　机电类比电路的四端网络Fig.3 Four-port network circuit

图3中，

(1)

I1，I2为流过支路的电流，物理中相当于振动速度。U1，U2为端口激励电压，物理中相当于激励力(声压)。根据基尔霍夫电压定律[7]，有式(2)成立。

(2)

通过式(2)可得到，

(3)

进一步可得到：

(4)

当目标处于静止安静状态时，U2=0，此时仅考虑U1的作用，系统函数为，

(5)

将式(1)代入式(5)，同时令s=jω，最终得到U2对I2作用的系统函数：

(6)

式中：A=D12D1D2m1m2，B=D12D1D2R1m2+D12D1D2m1R2，C=D12D1D2R1R2+D12D1m1+D12D2m2+D2D1m1+D2D1m2，D=D12D2R1+D12R2D2+D1R1D2+D1R2D2，E=D12+D1+D2

画出H12(s)的系统方框图，如图4所示。

图4中，各个系数的取值如式(7)所示。

a0=1

(7)

图4　系统方框图Fig.4 System block diagram

图4所示为一四阶微分方程，很难在时间域进行求解。式(6)所示的系统函数是连续的(s域)，若在数字域求解需将其转换成离散系统(z域)[8]，转换后有式(8)成立。

(8)

式中：N=4，b2n和a2n的取值与a2i(i=1,2,…,4)、b2i(i=0,1,2,…,4)及采样率fs有关。其等效方框图如图5所示。

图5　系统等效方框图Fig.54 Equivalent block diagram of the system

使用差分方程表示为：

(9)

对于二阶自由度的耦合系统，令I2受U1激励作用的系统函数为，

(10)

令I2受U2激励作用的系统函数为，

(11)

最终，I2可用如下等式表示，

L(I2)=L(U1)H12(s)+L(U2)H22(s)

(12)

式中：L(·)表示求拉普拉斯变换。

1.2多自由度耦合振动系统

若在现实中精细分析目标特性，目标不能够被等效为集中参数系统，目标(如球体)的每一部分都同时具有惯性、弹性和消耗能量的性质，是一个分布参数系统。对于这样的系统，使用两自由度建模是远远不够的，需等效成多阶自由度的耦合，如图6所示。

图6多阶自由度耦合

Fig.6 Multistage freedom coupled vibration

当系统为多自由度的耦合系统时，Ii使用如下式表示，

(13)

当目标和水介质均为静止安静状态时，目标只受到激励源Ul(入射声波)的作用(Uj=0，(j≠l))，式(13)变为

L(Ii)=L(Ul)Hli(s)

(14)

Hli可使用式(15)表达

(15)

式中：P为正整数，P=2Q，Q为耦合系统的阶数。对于离散系统(数字系统)，式(15)可使用如下式表示，

(16)

写成差分方程的形式如式(17)所示。

(17)

对比式(9)和式(17)可发现，当初始条件为安静静止时，多自由度耦合振动与两自由度耦合振动有相同的表达式结构，且方程的阶次等于自由度的平方。

1.3ARX模型

带有输入控制的自回归模型[9]使用如下式表示，

y(t)+a1y(t1)+…+anay(tna)=

b1u(tnk)+…+bnbu(tnbnk+1)+e(t)

(18)

式中：y(t)为t时刻的输出，na为极点个数，nb为零点个数加1，nk为输入对系统作用的延迟时间，e(t)为白噪声干扰。将式(18)写成精简的形式，

A(q)y(t)=B(q)u(tnk)+e(t)

(19)

式中：

(20)

对比式(17)、(18)可以发现，在单激励源作用下多自由耦合系统的强迫振动与ARX模型具有相似的结构，可以使用ARX模型构建。

2　浅海中目标回波模型

2.1目标直达入射声提取

多途效应是浅海环境下影响目标回波的一个关键因素，其典型的多途声线如图7所示。图7给出了声传播的三条主要声线，直达声和水面、水底反射声，各条声线相对目标的入射角度不同，目标受到的激励复杂。

图7　浅海中多途入射声线Fig.7 Shallow water multipath incident Rays

运用虚源法将界面的影响等效成自由场中的多个声源，如图8所示。

图8　多途的虚源等效Fig.8 The equivalent of Multi-path virtual source

使用多输入单输出的ARX模型构建上图的模型，如图9所示。

图9　浅海环境下目标入射波的ARX模型Fig.9 ARX model objects in shallow water waves

目标入射波等效为发射信号及其多个虚源经过各自的信道后到达目标体的线性叠加，使用多输入单输出的ARX系统进行建模。如式(21)所示。

Y=X1H1(s)+X2H2(s)+…+XnHn(s)=

(21)

Xi为虚源发出信号的拉氏变换，i为虚源的编号，N为虚源个数。xi由x0时移产生，

(22)

虽然Xi(s)可用X0(s)表示，使系统变为单输入单输出系统，但由于引入了非线性参数e-st0，所得到的表达式不满足单输入单输出的ARX模型，必须使用多输入单输出的ARX模型建模。

为方便求解，将式(21)表示成差分方程的形式。

A(q)y(t)=B1(q)x1(t-nk1)+

B2(q)x2(t-nk2)+…+

BN(q)xN(t-nkN)+e(t)

(23)

式中：

(24)

以入射信号及其虚源Xi作为ARX模型的输入，实测声信号Y为输出，估测ARX模型的参数，求解出Hi(s)(i=1,2,…,N)。

Yi=XiHi(s)

(25)

由式(25)可得出Yi，其中Y1是目标的直达声信号。

2.2目标直达回波提取

图10给出了在直达声作用下的三条目标回波声线，回波沿着入射路径在测量端汇聚叠加。假设浅海信道有N条多途子信道，则发射的声信号经过目标散射及多途作用后将在测量端存在N2条声线的叠加，最终在测量端得到的声信号成分复杂。

图10　直达声的多途回波Fig.10 The direct sound of multipath echoes

图11　目标回波模型Fig.11 The target echo models

在每一条入射声作用下，目标在多途中将产生N个信号沿不同路径到达测量端，考虑到一共有N条入射声线，所以一共有N2条声线，构成的多输入单输出的ARX模型如图11所示。

每条声线可用式(26)表示，

(26)

(27)

3　实验验证

实验环境为信道水池，水池深5 m，测量装置与目标均处于2.5 m深度，测量端与目标相距11.62 m，如图12所示。发射信号为线性调频信号(LFM)，信号脉冲宽度为2.5 ms，频率为50～60 kHz。

图12　水池实验示意图Fig.12 Tank Experiment sketch

图14(a)为换能器1发射的数字信号，图14(b)为水听器2接收到换能器发射的声信号，从图中可以看出，信号受多途影响严重，发生了很大畸变，信号幅度上起伏不定，时间上被延长。

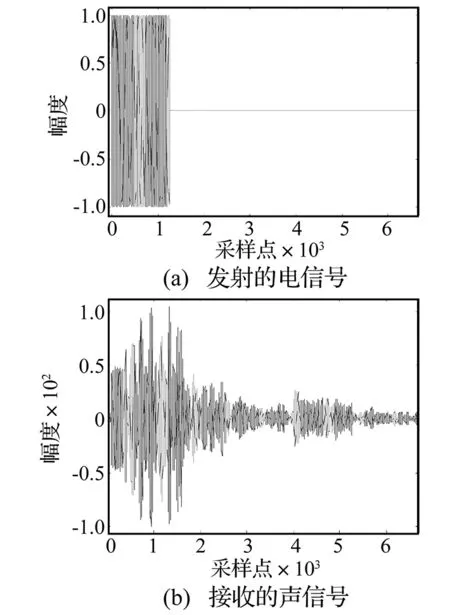
图13　信道水池实验Fig.13 Channel the tank test

对图13中信号做分数阶傅里叶变换(FRFT)[10]，取最优阶次的输出结果如图14所示。

图14　图8中信号FRFT变换后最优次输出Fig.14 Optimal FRFT transform output of Figure 8

从图14中得到7个主要波峰，代表多途的个数。其中右边的三个分别是直达波和水底、水面反射波。其他峰值为经界面多次反射后到达水听器的声波。从图中可观测到7条声线在u域的取值，换算成时间域，可得到各个声线的时延τi(i=1,2,…,7)。

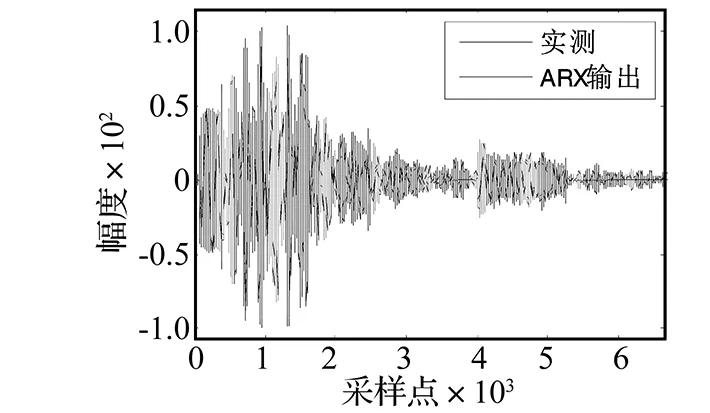
图15　ARX模型输出与实测输出Fig.15 ARX model output and the measured output

构建一个7输入1输出的ARX模型，模型的输入是图8中的声源(对应图12发射换能器1)及其虚源发出的信号，输出为图13(b)所示的实测声信号(由图12中水听器2接收)，求解ARX模型参数。ARX模型与实际的输出对比如图15所示。其中深色波形为目标端实测信号，浅色波形为ARX模型的输出，它们都具有很好的一致性。增大多途声线的个数可使两者的一致性更好，然而随着声线个数增加，模型的稳健性和有效性都将随之降低。

求解ARX模型的同时可得到各条子声信道的系统函数Hi(s)。由式(25)可得到各个子信道的输出波形。如图16(a)所示为ARX模型输出的直达波，图16(b)为通过消声水池中观测得到的直达波，对比两者可发现，信号整体上是一致的，说明该算法具有正确性。

图17(a)为水底反射的一次反射波，图17(b)为水面的一次反射波。可以看出，图中波形的包络不同，据此可推测水面和水底对声波的作用不同，具有不同的频率特性。图18为其余4条声线的输出波形。由于实验条件的限制，无法实测到水面和水底的一次及多次反射波，暂时无法对其进行实测对比分析。

图16　直达波Fig.16 Direct wave

图17　一次界面反射波Fig.17 The first interface echo

图18　其余声线的输出波形Fig.18 Remaining ray of the output waveform

对比图16(a)和图20可知，回波的包络与入射波的包络不同，反映出目标的频率选择特性；其次反射波信号的时间相比入射波长，说明目标对直达入射声有时间扩展作用。

声信号经历的多途路径越复杂、被界面反射的次数越多，信号的时延越大，所需的ARX模型阶次越高。对比图15和图19可以发现，信号的前段匹配效果好而后端差，图15的效果比图19效果好，这说明信号时延越长，经过的路径和耦合越复杂，所需阶次越高，声波信号越难匹配。目标的直达波以及直达回波未经过信道水面和水底的反射，其耦合振动过程简单，所需ARX模型的阶次低，求解的稳定性和可信度更高。

图19　建模获得的信号与实测目标回波Fig.19 Modeling signal and target echo

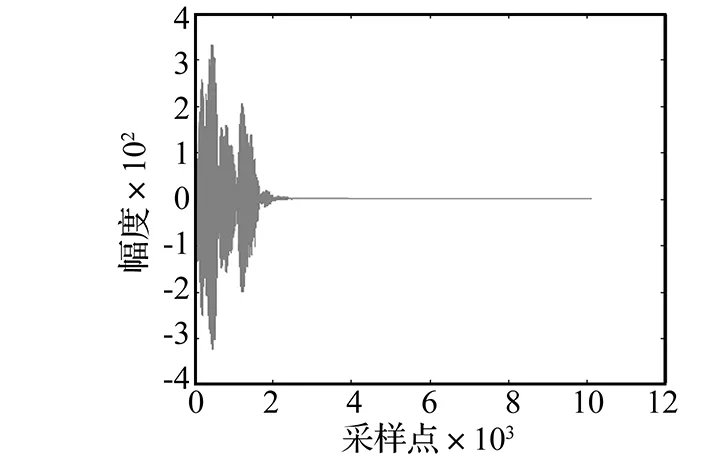
图20　直达入射声作用下的目标回波Fig.20 Direct echo of direct incident sound

本研究只需要提取目标直达声信号和直达信号下的直达回波，所求信号均在前端，因此求解时应优先考虑信号前端的匹配。

4　结　论

文章针对浅海环境下目标回波测试技术，从新的角度分析了声与目标的作用机制，提出了一种全新的分析液-固耦合振动方法。将声耦合振动模拟成随机过程中的ARX模型，将多途信道下声传播模型模拟成多输入单输出的ARX模型。通过有关水池实验研究，得到了以下结论：

(1) 多自由度耦合振动与两自由度耦合振动具有相同的表达式结构，且方程的阶次等于自由度的平方；

(2) 回声产生过程中，各个声激励源对回声的影响是线性叠加关系，为浅海多途声信号的分解奠定了理论基础；

(3) 声的耦合振动模型与ARX模型具有相似的表达式，可使用ARX模型对耦合振动进行建模；结合虚源法和多输入单输出的ARX模型，可求解出多途各个子信道的信号及信道响应；

(4) 随着子信道的时延增大，所需ARX模型的阶次需对应不断增加；求解时优先保证回波前端匹配，可保证目标直达入射波、直达回波及其响应函数求解的有效性。

[1] Abraham D A, Willett P K. Active sonar detection in shallow water using the page test[J]. Oceanic Engineering, IEEE Journal of, 2002, 27(1): 35-46.

[2] Chen Q, Xu W, Pan X, et al. Wideband multipath rejection for shallow water synthetic aperture sonar imaging[J]. IET Radar, Sonar & Navigation, 2009, 3(6): 620-629.

[3] Xu B, Zhang H, Zeng L, et al. Application of parameter-induced stochastic resonance to target detection in shallow-water reverberation[J]. Applied Physics Letters,2007,91(9): 091908.

[4] Sarkissian A. Extraction of a target scattering response from measurements made over long ranges in shallow water[J]. The Journal of the Acoustical Society of America,1997,102(2): 825-832.

[5] Harrison C H, Nielsen P L. Multipath pulse shapes in shallow water: Theory and simulation[J]. The Journal of the Acoustical Society of America, 2007, 121(3): 1362-1373.

[6] 何祚镛, 赵玉芳. 声学理论基础[M]. 北京:国防工业出版社,1981:5-28.

[7] 嵇英华, 刘清主编. 电路分析[M]. 北京:电子工业出版社,2014.

[8] 信号与系统[M]. 西安:西安交通大学出版社,1998,471-477.

[9] 潘仲明. 随机系统与系统[M]. 北京:国防工业出版社,2013:214-225.

[10] Namias V. The fractional order fourier transform and its applicationin to quantum mechanics[J]J Inst Appl Math,1980,25(3):241-265.

Shallow sea target echo tests and target response solving

HE Cheng1,2, ZHAO Anbang1,2

(1. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China;2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China)

Using the liquid-solid coupled vibration model, the shallow sea target echo generation mechanism was modeled and the coupled vibration formulas were denived. The target echo expressions under conditions of single- and multi-excitation sources were deduced. The target echo generation mechanism was analyzed from a new view point by building the target model with ARX model in random processes. The multi-input single-output ARX model was used to build the target echo test model in shallow sea environment. At last, the target direct incident ware and direct echo wave were solved. The influence of a multi-channel path was eliminated effectively. The measurement results being equivalent to those measured in the free field were obtained. The effectiveness of the proposed algorithm was verified with pool experiments finally.

shallow sea channel; coupled vibration; target echo; ARX model

国家自然科学基金(11374072;61371171)

2014-11-05修改稿收到日期：2015-07-16

何呈 男，博士生，1987年12月生

赵安邦 男，博士，教授，博士生导师，1978年1月生

E-mail:zhaoznbang@hrbeu.edu.cn

TB56

A

10.13465/j.cnki.jvs.2016.15.003