驳船斜撞刚性墙动力时程概率模型

王君杰， 陈传景， 宋彦臣， 张　龙

(1.同济大学 土木工程防灾国家重点实验室，上海　200092; 2.天津市市政工程设计研究院，天津　300051)



驳船斜撞刚性墙动力时程概率模型

王君杰1， 陈传景1， 宋彦臣1， 张龙2

(1.同济大学 土木工程防灾国家重点实验室，上海200092; 2.天津市市政工程设计研究院，天津300051)

考虑到船桥碰撞的随机性，为获得驳船斜撞刚性墙的撞击动力时程概率模型样本，建立了6艘不同吨位的代表性驳船有限元计算模型，利用LS-DYNA有限元软件进行数值模拟计算，获得了6个不同撞击速度下36条船撞动力时程样本曲线。将样本曲线无量纲化，得到了无量纲的船撞动力时程，以及撞击力均值和持续时间的参数表达式。采用21个离散点近似表示无量纲化曲线，统计分析表明各离散断面上的无量纲撞击力符合正态分布，并得到各离散断面无量纲撞击力的均值和标准差。根据随机数生成技术，生成驳船斜撞刚性墙动力时程样本。通过人工随机生成的概率模型样本与数值模拟计算得到的样本进行比较，确定该技术方法的精度较好。

驳船；刚性墙；数值分析；概率模型；船撞动力时程；无量纲化；LS-DYNA

国内外桥梁船撞设计规范或指南[1-4]中，船撞作用多被等效为静力荷载。但船撞桥是一个冲击过程，等效静力分析不能反应动力特征。碰撞有限元分析已经在桥梁船撞研究和设计中得到广泛应用，但碰撞计算繁琐、计算量巨大，且要求计算人员具有良好的冲击力学知识、有限元理论和方法、软件使用技巧，不是一般的桥梁设计工程师所能高质量完成的工作。因此建立面向工程设计应用的(面向工程设计规范的)的简化荷载模型具有实用价值。2002年，欧洲统一规范[4]给出了用于弹性分析和弹塑性的两种简化的船舶撞击力时间过程模型，见图1。欧洲统一规范的作法是在设计中考虑船舶对桥梁冲击效应的好的开端，但模型参数确定的数据基础不足，因此模型的形式和参数的确定还需要发展和完善。

图1　船舶冲击的荷载-时间函数Fig.1 The Impact Load function of ships

图1中，tr是弹性作用时间(s);tp是塑性撞击时间(s)；te是弹性响应时间(s)；ta是等效撞击时间；ts是总撞击时间(s)；C(船的弹性刚度)=60 MN/m；F0(弹性-塑性极限力)=5 MN；xe(弹性变形)=0.1 m；vn(船只到撞击点的垂直速度)：如果是正面撞击，vn是航行速度v；如果是侧面撞击，vn=vsina。

船撞桥是一个复杂的问题，具体碰撞情况受到多种复杂因素的影响，包括船舶吨位、撞击速度、被撞物的刚度、船舶及船艏结构形式、压仓排水量及被撞物的几何特征等不确定性因素都会对撞击力产生显著的影响船桥实际发生碰撞时很难记录其撞击力，原型船舶撞击桥梁结构的实验也不现实，而有限元仿真分析是一种有效而经济的手段被越来越多的学者采用[5-7，9-13]。本文选取6艘代表性单机驳船，吨位从90DWT-2000DWT，进行了碰撞刚性墙的计算，获得了6个不同撞击速度下的36条撞击力时间过程样本。通过对这些数据的统计分析，建立了撞击力时间过程的概率模型。本文的碰撞计算采用LS-DYNA软件完成。

1　碰撞数值模拟

1.1碰撞模型

船-桥碰撞事故调查资料显示[14]，船艏撞击事故占很大的比例,本文考虑这种碰撞形式。桥墩的柔度会引起撞击力的降低，但桥墩的柔度受很多复杂因素影响，若考虑其影响将使简化撞击力时间过程模型过分复杂而失去意义。因此本文将被撞桥梁构件看成是刚性平面(如图2所示)，这样处理得到的撞击峰值是偏于保守的[4]。另外，桥墩的几何、船舶与桥墩的位置关系、风和水流、船舶遭遇障碍物时的紧急处置等因素影响到船舶碰撞桥墩时的角度和部位，驳船头前端面与桥墩(塔)、承台平面理想化的面-面全接触正撞的可能性极低，船-桥碰撞事故调查表明了这一点。因此确定驳船与桥梁的撞击方向时，考虑一个偏角的合理的作法，本文采用5°的碰撞偏角，如图2所示。

图2　驳船斜撞刚性墙模型Fig.2 The oblique collision model of barge-rigid wall collision

1.2代表船舶基本参数

本文选取了6艘不同吨位(90DWT-2000DWT)的驳船进行碰撞模拟计算，以获得其对刚性墙面的撞击力时间过程。驳船特征参数如表1所示，典型单机驳船的船艏结构形式如图3所示。

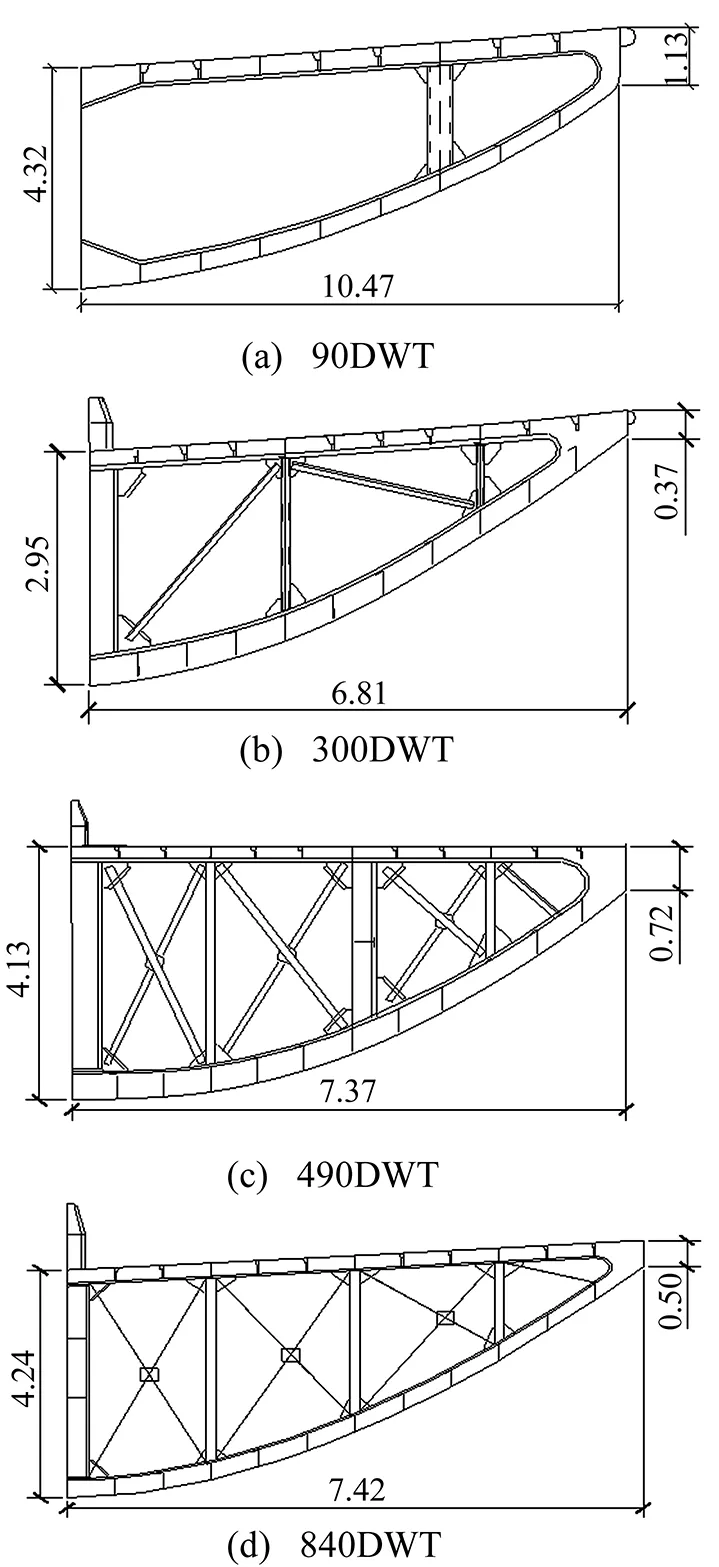
图3　部分驳船船艏结构纵剖图Fig 3 Bow profiles of typical barges

1.3碰撞计算建模

碰撞计算采用LS-DYNA软件完成。驳船有限元模型采用壳单元SHELL163，有弯曲和膜特征，可以更好地模拟出钢板的翘曲变形和材料失效。为了模拟碰撞中船艏碰撞部位钢板的大变形、屈服以及船体内部钢板自接触等力学行为，船艏部分采用单元网格加密处理；另外，为了减少计算分析时间，船舶后部不参与碰撞的有限单元划分稀疏一些。见图4。

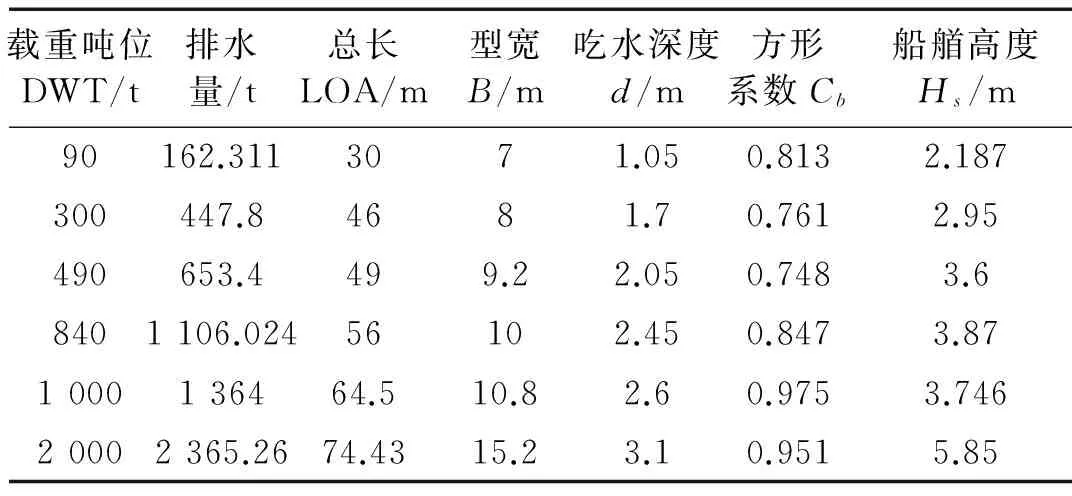
表1　代表吨位驳船基本数据

图4　部分驳船计算有限元模型图Fig.4 FE modellings of typical barges

船舶钢板的本构模型采用LS-DYNA中的双线性弹塑性模型描述，采用Cowper-Symonds方程描述钢材在冲击荷载下的应变率效应，该模型的屈服函数φ：

(1)

式中:ξij表示相对于屈服中心的偏应力；σy为屈服应力，可表示为：

(2)

船舶钢板本构模型参数取值如表2所示。刚性墙有限元模型采用刚体材料定义，材料参数使用混凝土材料的密度、杨氏模量和泊松比，如表3所示。计算中材料接触的静力摩擦因数和动力摩擦因数分别取0.3和0.2。

表2　驳船钢板本构参数取值

表3　刚性墙本构参数

计算中船舶撞击速度取为1 m/s、2 m/s、2.5 m/s、3 m/s、4 m/s、5 m/s，共进行了36个工况的碰撞计算。

1.4撞击力时程曲线样本

根据数值仿真计算结果，典型的驳船斜撞刚性墙撞击力时程如图5所示。

对撞击动力时程样本曲线的观察发现：① 样本曲线可大致分为三段，即快速上升段，缓慢上升或者下降段，快速下降段；② 随着船舶吨位和撞击速度的增大，撞击力峰值及持续时间也增大。

图5　船撞动力时程曲线举例Fig.5 Example curves of the impact force history

2　撞击力时程经验概率模型

2.1无量纲撞击力时间过程

为观察撞击力时间过程的特征，将所有的样本曲线无量纲化，具体处理方法是：

(3)

(4)

(5)

式中：T为撞击力持续时间(s)，τ为无量纲时间，Fmean为撞击力均值(MN)，F(t)为t时刻的撞击力(MN),β(τ)为无量纲撞击力比值。

图6是36条标准化的驳船斜撞动力时程曲线，可以看到，虽然驳船的吨位、速度的差异会引起曲线的不同，但形状函数β(τ)的总体变化趋势明显；同时可以看到，在标准化时间断面上β(τ)具有一定的离散性。为考虑这种离散性，本文将标准化时间断面上β(τ)的取值作为随机变量处理，这样β(τ)就是一个随机过程。经过上述处理之后，驳船的撞击力简化模型可以用撞击力持续时间T、撞击力均值Fmean、和形状函数β(τ)来表达。

为得到β(τ)的统计分布，将无量纲时间等间隔离散为21个时刻点，每个时刻点对应36个样本值，见图7。由于00和20断面处的β(τi)，i∈[00,20]值很小，所以将这两个时刻点的β(τi)取确定的值，即0。假定01-19断面处的β(τi)符合正态分布，对每个断面上的数据进行χ2假设检验，结果表明在0.05显著水平下接受假设，如图8所示,这表明无量纲化的撞击力样本符合正态分布。根据均值与方差的无偏估计，各离散断面β(τi)的均值和标准差见图9。

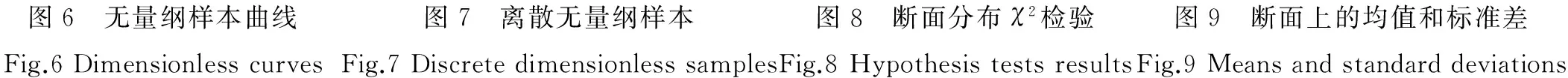
图6 无量纲样本曲线Fig.6Dimensionlesscurves图7 离散无量纲样本Fig.7Discretedimensionlesssamples图8 断面分布χ2检验Fig.8Hypothesistestsresults图9 断面上的均值和标准差Fig.9Meansandstandarddeviations

2.2撞击力均值及持续时间

为确定撞击力持续时间T和撞击力均值Fmean，将36种荷载工况下的Fmean和T关于吨位DWT和速度v进行拟合。根据36条撞击力时间过程样本曲线计算得到的撞击力均值Fmean见表4，撞击持续时间T见表5。

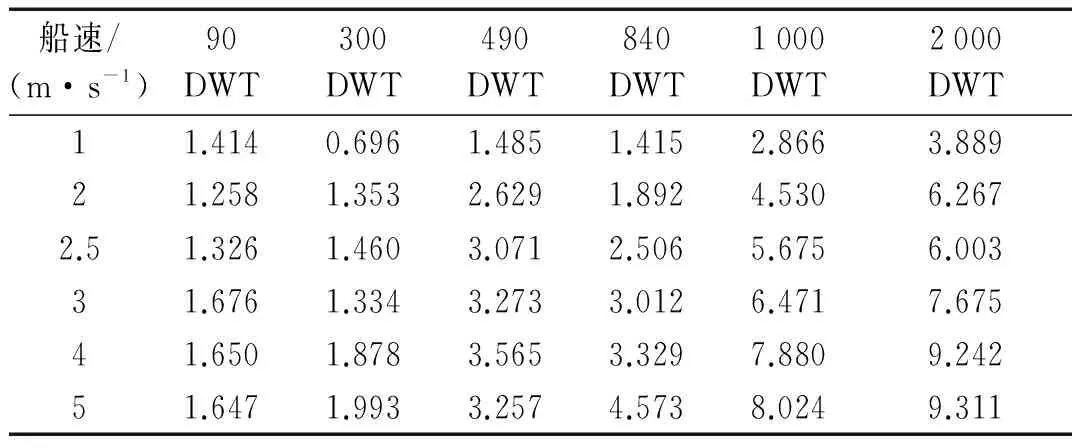
表4　驳船在不同初始速度下的平均撞击力(MN)

假定平均撞击力Fmean和撞击力持续时间T可以用幂指数函数表达，即：

Fmean=F0·vaDWTb

(6a)

T=T0·vaDWTb

(6b)

根据表4和表5的数据进行数据拟合，获得模型参数。数据拟合分两步进行：① 将不同速度v下的Fmean(或T)按式Fmean=cDWTb进行拟合，得到参数bi的数值，并将其平均值作为b的最终取值；② 第一步中得到的c值与速度有关，仍然假定为幂指数函数形式，进行数据拟合，得到a和F0(或T0)。拟合过程见图10～13，模型参数的拟合结果见表6。

表5　驳船在不同初始速度下撞击力的碰撞持续时间(s)

2.3拟合误差分析与修正

根据式(6)和表6可以计算出持续时间T和平均撞击力Fmean的拟合值，由式(7)和(8), 得到冲量的拟合值和冲量的拟合误差百分比，见表7。

表6　模型参数拟合结果

(7)

(8)

图10 不同速度下Fmean和DWT的关系Fig.10ThefittedrelationshipofFmeanandDWT图11 Fmean中的常数拟合成v的函数Fig.11ThefittedfunctionofFmean图12 不同DWT下T和v的关系Fig.12ThefittedrelationshipofTandv图13 T中的常数拟合成DWT的函数Fig.13ThefittedfunctionofT

表7　冲量的拟合误差百分比

由于船撞刚性墙是一个动力持时过程，冲量拟合值应该与原始冲量值大致相等，因此将得到的冲量的拟合误差值对DWT和v进行拟合修正。拟合分三步进行：① 将冲量误差值对速度进行拟合，得到式(9a)和参数k2的数值，并将其平均值0.484作为k2的最终取值；② 将式(9a)中的k0、k1拟合成线性关系，结果见式(9b)；③ 将式(9b)中的k1对DWT进行指数函数拟合，结果见式(9c)。拟合过程见图14～图16。

error(DWT,v)=k0-k1k2v

(9a)

k0=-0.211(k1-4.283)

(9b)

k1=2.926+5.732×0.993DWT

(9c)

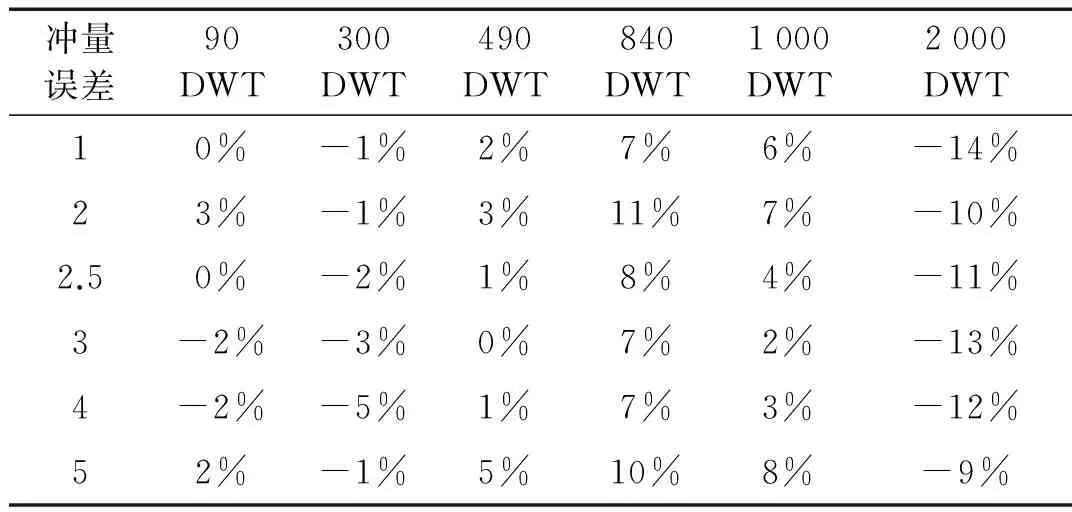
表8　修正之后的冲量拟合误差值

图14 不同速度下的冲量拟合误差值Fig.14Fittingerrorvalueofdifferentvelocity图15 k1与k0的线性拟合关系Fig.15linearfitrelationshipofk1andk0图16 k1拟合成DWT的函数Fig.16Thefittedrelationshipofk1andDWT

3　撞击力样本过程的生成

3.1无量纲随机样本

根据建立的β(τ)的概率模型，采用Matlab计算机语言编制了程序，生成01～19断面共19个均匀分布的随机数，得到00～20 断面上的无量纲撞击力β(τ)，把各个断面的值以直线相连便得到了形状函数β(τ)；根据式(6)计算Fmean和T，式(8)和(9)计算冲量误差修

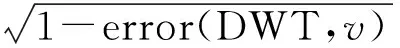
(a) β(τ)均值误差(b) 撞击力样本(c) 撞击力样本图16 随机生成样本均值与原始样本均值的对比Fig.16Thecomparisonofthemeanimpactforcebetweenthegeneratedcurvesandoriginalcurves

3.2简化动力时程比较

由AASHTO和中国《铁路桥涵设计基本规范》中给出的驳船撞击力估算公式得本文各工况下的等效静力值，比较结果如图16所示。490DWT驳船在2.5 m/s下的等效静力与有限元分析得到的撞击力在时域上的平均值很接近，2000DWT驳船在1 m/s下的等效静力与有限元得到的撞击力最大值很接近，比较结果可确定，有限元模型是合理的，简化的时程动力概率模型吻合度较高。

4　结　论

本文选择了具有代表性的6艘单机驳船，吨位从90DWT-2000DWT，采用LS-DYNA软件对其进行了碰撞建模，完成了36种工况的驳船撞击刚性墙的计算，获得了36条撞击力时间过程样本曲线。通过对36条样本曲线的统计分析，得到了以下结果和结论：

(1) 对样本曲线进行了时间和力的双轴无量纲化处理，统计分析表明各时刻断面处的无量纲撞击力符合正态分布；

(2) 通过回归分析，给出了撞击力均值和持续时间均值与驳船吨位DWT、撞击速度v的关系表达式；

(3) 建立了驳船撞击力动力时程的概率模型，实现了撞击力时间过程样本的生成。比较结果表明，所提出的撞击力概率模型和确定的参数具有合理性。

需要说明的是，本文选取的驳船数量为6艘，数量有限。为得到更合理的模型参数，需要进一步完成原始样本的数据积累，增加原始样本的容量和代表性。这是一项长期的工作。

[1] AASHTO. Guide specification and commentary for vessel collision design of highway bridges(second edition)[S]. WashingtonD.C.:American Association of State Highway and Transportation Officials, 2009.

[2] 公路桥涵设计通用规范:JTJ D60—2004[S]．北京：人民交通出版社，2004.

[3] 铁路桥涵设计基本规范:TB10002．1—1999[S]．北京：人民交通出版社，1999.

[4] NBN EN 1997-1-7：2006.Eurocode 1: Actions on structures-Part 1-7: General actions—Accidentalactions[S]. British Standards Institution, London, 1991.

[5] Cowan D R. Development of time-history and response spectrum analysis procedures for determining bridge response to barge impact loading[D]. University of Florida, 2007.

[6] Consolazio G R, Davidson M T. Simplified dynamic analysis of barge collision for bridge design[J]. Transportation Research Record: Journal of the Transportation Research Board, 2008, 2050(1): 13-25.

[7] Davidson M T,Consolazio G R, Getter D J. Dynamic amplification of pier column internal forces due to barge-bridge collision[J]. Transportation Research Record: Journal of the Transportation Research Board, 2010, 2172(1): 11-22.[8] 王君杰,范立础.建立桥梁船撞动力设计理论与方法的建议[C]//第18届全国桥梁学术会议论文集(下册), 天津,2008:943-949.

[9] 王君杰，卜令涛，孟德巍．船桥碰撞简化动力分析方法：简化动力模型[J]．计算机辅助工程，2011，20(1)：70-75．WANG Jun-jie，BU Ling-tao，MENG De-wei．Simplified dynamic analysis method of ship-bridge collision： simplified models [J]．Computer Aided Engineering，2011，20(1)：70-75.

[10] 孟德巍，王君杰，卜令涛．船桥碰撞简化动力分析方法：简化模型的精度[J]．计算机辅助工程，2011，20(1)：76-80．

MENG De-wei，WANG Jun-jie，BU Ling-tao．Simplified dynamic analysis method of ship-bridge collision：Precision of Simplified Method [J]．Computer Aided Engineering，2011，20(1)：76-80．

[11] 王君杰, 宋彦臣, 卜令涛. 桥墩船撞力时间过程概率模型[J]. 公路交通科技, 2014, 31(1): 82-88.

WANG Jun-jie, SONG Yan-chen,BU Ling-tao. Probabilistic model of impact force for vessel-bridge collision[J].Journal of Highway and Transportation Research and Development,2014,31(1):82-88.

[12] 王君杰, 宋彦臣, 卜令涛. 船舶与桥墩撞击力-撞深关系概率模型[J]. 中国公路学报, 2014, 27(6): 59-67.

WANG Jun-jie, SONG Yan-chen,BU Ling-tao. Probabilistic model of impact force-penetration for ship-bridge collision[J]. China Journal of highway and Transport, 2014, 27(6): 59-67.

[13] 曹聪慧，驳船对桥梁冲击的简化静动力荷载[D]. 上海:同济大学, 2011.

[14] 戴彤宇,聂武刘,刘伟力. 长江干线船撞桥事故分析[J].中国航海,2002(4):44-47.

DAI Tong-yu，NIE Wu-liu,LIU WEI-li．The analysis of ship-bridge collision in main waterway of the yangtze river [J]．Navigation of China，2002(4)：44-47

Probabilistic model for dynamic time history of a barge-rigid wall oblique collison

WANG Junjie1, CHEN Chuanjing1, SONG Yanchen1, ZHANG Long2

(1. State Key Laboratory of Civil Engineering for Disaster Reduction, Tongji University, Shanghai 200092, China;2. Tianjin Municipal Engineering Design & Research Institute, Tianjin 300051, China)

Considering the random nature of a barge-bridge collision, 6 barges with different tons were modeled to get the dynamic time history probabilistic model samples of a barge-rigid wall oblique collision. FE software LS-DYNA was used for numerical simulation, and 36 sample curves of the dynamic time history with 6 velocities were obtained. These sample curves were non-dimensionalized, and dimensionless curves of dynamic time history were obtained. Furthermore, the expressions of mean impact force and duration versus tonnage and velocity were derived. 21 discrete points were used to express the dimensionless curves approximately and statistical analysis was conducted at each discrete point. The results showed that the dimensionless impact forces of each discrete section are normally distributed, and then their mean values and standard deviations are obtained; according to the random number generation technique, the sample curves of a barge-rigid wall oblique collision are generated. Comparing the artificial probabilistic model samples with numerical simulation ones, it was verified that this technical approach has a better accuracy.

barge; rigid wall; numerical simulation; probabilistic model; impact force time history; non-dimension; LS-DYNA

国家自然科学基金(51278373)；国家自然科学基金会重点(5143801)；国家重点基础研究发展计划(2013CB036305)；交通部西部科技(200731882234)；交通运输部行业联合科技攻关(2008353344340)

2015-06-10修改稿收到日期：2015-08-17

王君杰 男，博士，教授，1962年12月生

U442.59

A

10.13465/j.cnki.jvs.2016.15.004