腹板开孔的箱型梁结构噪声辐射特性分析

刘林芽， 许代言

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌　330013)



腹板开孔的箱型梁结构噪声辐射特性分析

刘林芽， 许代言

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌330013)

箱型梁结构在列车的动力作用下产生振动并引发低频噪声，这种低频噪声对人体健康危害很大。以单跨32 m轨道交通箱型梁为研究对象，分别建立腹板无孔与腹板开孔两种工况下的三维实体有限元模型；在计算列车荷载作用下箱型梁振动响应的基础上，采用有限元-边界元耦合声学求解方法，分析计算腹板开孔的箱型梁结构噪声辐射特性。结果表明：腹板开孔使箱型梁跨中顶板和底板的垂向振动均有所降低；腹板开孔使箱型梁结构噪声衰减方向发生改变，在梁体下方及远场点有较好的降噪效果，分析结果可为城市轨道交通箱型梁的结构减振降噪设计提供一定的理论参考依据。

箱型梁；腹板开孔；结构噪声；有限元；边界元

轨道交通箱型梁在列车荷载作用下产生振动，并向周围环境辐射噪声，其中0～100 Hz频段的噪声称为低频噪声[1-2]。这种低频噪声波长较长，在传播过程中不容易衰减，对人体健康危害极大[3-4]，因此有必要针对轨道交通箱型梁的结构噪声展开研究并采取有效措施加以控制。

影响轨道交通箱型梁低频振动与噪声辐射的因素很多，车速、桥梁结构外形和高架系统设计的不同均可造成结构噪声峰值频率的不同[5]。箱型梁断面等因素对高架桥梁结构的振动传递特性也会产生影响[6]。列车荷载引发轨道结构及其下部桥梁结构振动，进而引发二次辐射噪声，其辐射噪声取决于桥梁的阻抗，一般桥梁阻抗越大，辐射噪声越小[7]。圆柱壳上开孔的方案可以降低结构的低频噪声，这为降低桥梁的结构噪声提供了一种思路[8]。在车轮辐板上开设孔洞，可以使辐板内外侧形成“声短路”来降低车轮的声辐射效率[9-10]。工程实践中为了调节箱型梁结构腔室内外温差，减小结构由于温度产生的非受力裂缝，在设计中通常在腹板上开设通气孔，箱型梁腹板开设通气孔对结构噪声辐射的影响未见有文献报道。

本文以某32 m轨道交通箱型梁为研究对象，分别建立腹板无孔与腹板开孔两种工况下的三维实体有限元模型；在计算列车荷载作用下箱型梁振动响应的基础上，采用有限元-边界元耦合声学求解方法，分析计算腹板开孔的箱型梁结构噪声辐射特性，并对腹板开孔措施的降噪效果进行分析。

1　箱型梁有限元-边界元耦合声学计算模型

1.1箱型梁有限元分析理论与模型的建立

在有限元分析中，本文采用瞬态动力学分析结构的动力响应，得到在随时间变化的荷载作用下结构节点位移、应力、速度、加速度等的响应。瞬态动力学分析也称为时间历程分析，其基本运动方程为：

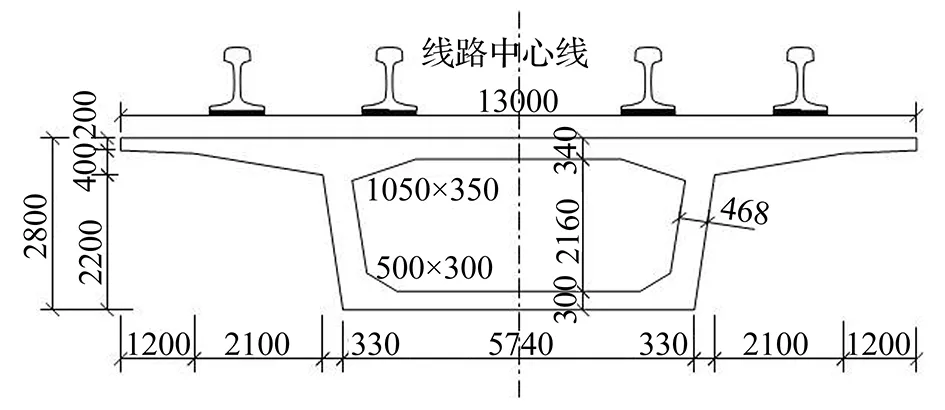
图1　箱型梁截面尺寸Fig.1 Cross section size of box beam

为了比较准确地预测列车荷载作用下轨道交通箱型梁振动与结构噪声的辐射情况， 用有限元软件建立箱型梁三维实体有限元模型，箱梁跨度为32m，截面尺寸选用图1所示某高架桥实际尺寸，弹性模量取36.2GPa，密度2 500kg/m3，泊松比为0.2，阻尼比为0.03，支座刚度取3.38×109N/m；扣件垂向刚度为6×109N/m。阻尼为104Ns/m，扣件间距为0.625m，划分网格后的有限元模型如图2所示。

图2　箱型梁实体有限元模型Fig.2 Finite element model of box beam

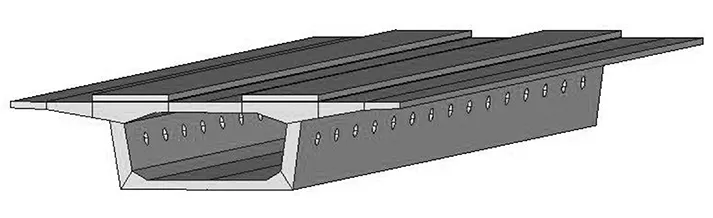
图3　腹板开孔的箱型梁有限元模型Fig.3 Finite element model of box beam with web hole

本文旨在分析腹板开孔的箱型梁的结构噪声辐射特性，腹板开孔半径取0.1m、间距2m，腹板开孔的箱型梁有限元模型如图3所示。开孔尺寸和位置满足 《混凝土结构构造手册》中梁腹圆形孔洞的要求[11]，详见表1。

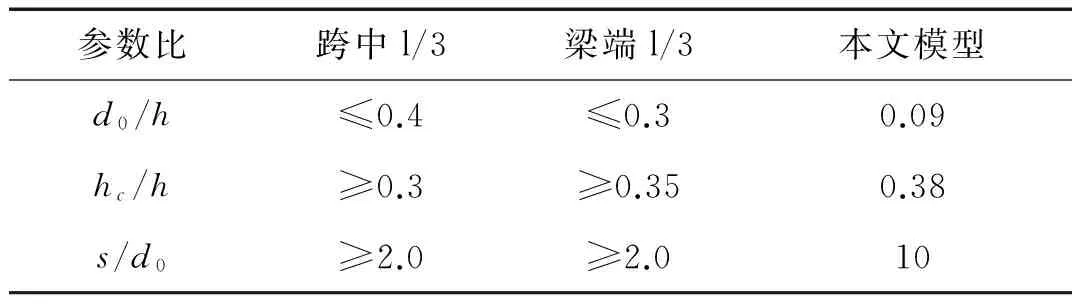
表1　 圆孔洞尺寸及位置

注：d0指圆孔直径；h指梁腹高度；hc指圆孔上部距梁腹顶端距离；s指孔间距。

1.2箱型梁辐射噪声计算理论与边界元模型的建立

根据流体介质的守恒原理和关于声波动的一些基本假设，可知箱型梁声辐射的Helmholtz方程表达式如下：

(2+k2)p=0

(2)

由于在声场和固体结构耦合边界上，重合的点具有相同的边界条件，因此知道了固体边界上的位移响应结果，就可以计算声场边界上的声压，进而求得整个声场中任意一点的声压。基于有限元-边界元耦合声学计算方法求解大规模复杂结构的振动噪声水平与试验测试数据相比有较高的准确性[12]。

图4　箱型梁声学边界元模型及场点网格Fig.4 Acoustic boundary element model of box beam and sites box beam grid

基于有限元-边界元耦合声学求解理论建立了箱型梁边界元模型。在建立声学边界元模型时，考虑最大单元的边长要小于计算频率最短波长的1/6，即最大单元的边长要满足如下表达式：

(3)

式中:c为声音在空气中的传播速度，取340 m/s；本文采用的间接边界元法，箱型梁边界元网格划分最大单元尺寸L为0.32 m，由式(3)可知该模型的最大计算频率可以达到177 Hz。箱型梁边界元网格如图4所示。

2　箱型梁自振特性分析

了解桥梁结构的自振频率对掌握其动力性能和外荷载作用下的动力响应有着重要的意义。所以在进行桥梁结构瞬态动力分析之前,需要对桥梁结构进行模态分析。模态分析中模态的提取方法采用Block Lanczos法。通过模态分析计算结构的固有频率和振型,即可了解这些模态被激活时结构如何响应,桥梁结构的前十阶自振特性见表2。

表2　前十阶振型描述

由表2可见，腹板开孔的箱型梁自振频率较无孔模型有所提高，但振型基本相似，均在第7阶出现面板局部振动，频率均在20 Hz附近范围内，振型可见图5。

图5　两种箱型梁第7阶模态对比图Fig.5 Two kinds of box beam seventh modal contrast figure

3　列车荷载作用下箱型梁振动响应分析

3.1轮轨力求解与加载

轨道不平顺引起了轮轨之间的相互作用，是箱梁产生振动的来源，为了预测箱梁振动产生的噪声，我们先要模拟轮轨之间的相互作用力。本文采用2节CRH2列车模拟加载，计算速度为180 km/h，列车基本参数见表3。

表3　列车基本参数

本文采用德国低干扰谱作为轮轨表面不平顺激励，轨道不平顺谱波长范围是5 mm～300 mm。运用车辆-轨道耦合动力学原理，将钢轨视为连续弹性离散点支承的Timoshenko梁，轨道板视为连续均布弹性基础上的自由梁，轨下胶垫和扣件系统用离散分布的黏滞阻尼和线性弹簧模拟，轨道板下面的沥青垫层利用连续分布的阻尼和线性弹簧表示，轮轨之间的接触采用Hertz非线性接触理论进行处理[13]，建立板式无砟轨道垂向耦合双层梁模型,利用Newmark积分方法求解车辆-轨道耦合振动模型的动力微分方程[14]，最终得到轮轨相互作用力如图6所示。

图6　轮轨垂向力时程曲线图Fig.6 Time-step curves of vertical force between wheel and rail

将列车实际运行过程简化为一系列随时间移动的集中力荷载，本文采用右线单向加载方式初步分析腹板开孔的箱型梁的结构噪声辐射特性，每节列车按轮对左右对称分布共8个集中力荷载，加载时间步长为6.4×10-4s。

3.2箱型梁振动响应

为了研究轨道交通箱型梁在列车荷载作用下的振动及频响特性，选取图7所示的箱型梁跨中截面振动响应输出点，1～4号输出点分别表示箱型梁跨中顶板、底板、腹板中心及翼缘端点。将上述求解的轮轨作用力作为激励源，采用完全法对轨道交通箱型梁有限元模型进行瞬态响应分析，通过傅里叶变换对箱型梁结构振动响应进行频谱分析得到如图8～图12所示 1～4号输出点的加速度频谱曲线。

图7　箱型梁跨中截面振动响应输出点Fig.7 The vibration response output point in midspan of box beam

图8　输出点1垂向振动加速度Fig.8 Vertical vibration acceleration of point 1

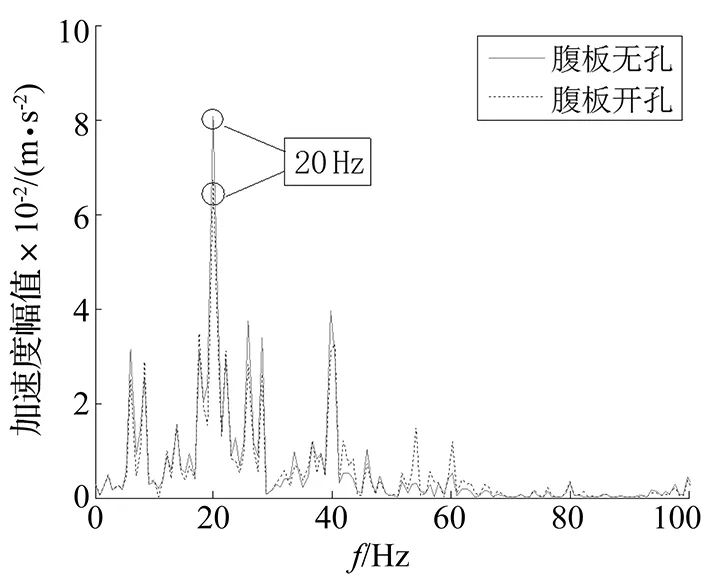
图9　输出点2垂向振动加速度Fig.9 Vertical vibration acceleration of point 2

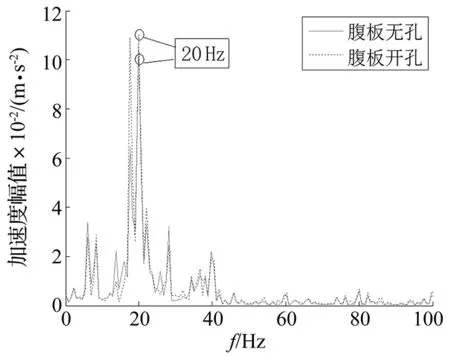
图10　输出点3垂向振动加速度Fig.10 Vertical vibration acceleration of point 3

由图8～图12可见，列车通过箱型梁时，各振动输出点的加速度响应主要分布在20～40 Hz范围内，这一计算结果与文献[15]采用移动质量模型计算得到的结果一致，说明本文建立的箱型梁有限元振动模型具备一定的准确性。

图11　输出点3横向振动加速度Fig.11 Lateral vibration acceleration of point 3

图12　输出点4垂向振动加速度Fig.12 Vertical vibration acceleration of point 4

由图8、9可知，腹板开孔对箱型梁的跨中顶板和底板中心部位在20 Hz峰值频率处有较好的减振效果；从图10～图12可见，在20 Hz峰值频率处，腹板开孔对箱型梁腹板与翼缘的垂向振动以及腹板横向振动均有不同程度的加强，由此需要进一步针对腹板开孔措施对箱型梁噪声辐射特性的影响进行计算分析。

4　箱型梁声辐射特性分析

4.1场点声压级

将箱型梁的结构振动响应作为声学边界元初始条件，基于声学边界元软件virtual.lab求解场点声压响应。为了研究距桥体中心线水平向不同距离处腹板开孔的箱型梁的声场分布规律，分别沿水平向选取5个场点进行分析。 D1～D5于跨中距地面1 m的位置垂直于线路中心线分布，距桥体中心线水平距离分别为0 m、5 m、10 m、20 m、25 m。箱型梁跨中声场输出场点分布见图13。

图13　箱型梁跨中声场输出场点分布图Fig.13 Sound point distribution in middle span of box beam

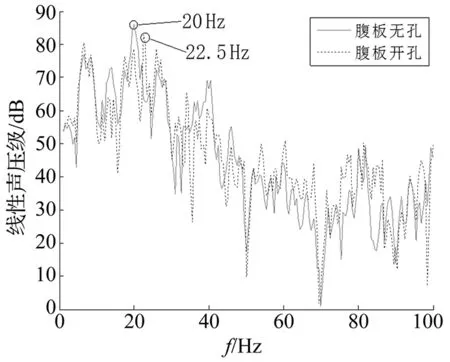
图14　场点1噪声辐射声压级 Fig.14 Sound pressure level of sites 1

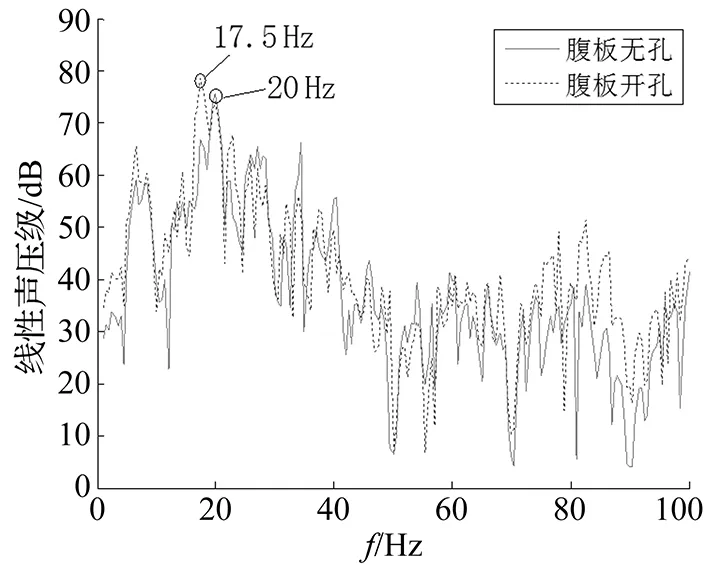
图15　场点5噪声辐射声压级Fig.15 Sound pressure level of sites 5

场点D1和场点D5的噪声辐射声压级分别如图14、15所示。箱型梁结构噪声辐射以20～40 Hz低频为主，噪声辐射的峰值频率为20 Hz；由表2和图5箱型梁模态分析可知，在中心频率20 Hz带宽内，腹板无孔箱型梁振动频率为22.99 Hz，腹板开孔箱型梁振动频率为24.65 Hz，结构低阶局部振动容易被激发，导致结构噪声辐射水平最高。这一原理与文献[16]中试验验证分析得到的结论一致。

场点D1位于箱型梁桥体正下方距地面1 m处，由图14可知，腹板开孔后箱型梁在20 Hz处等效声压级有所降低；但箱型梁腹板开孔后结构噪声辐射的峰值频率变为22.5 Hz，较无孔箱型梁有所提高，在22.5 Hz处腹板开孔的箱型梁噪声辐射声压级较无孔模型20 Hz处的峰值声压仍降低3 dB左右。

场点D5位于箱型梁桥体中心线水平距离25 m处，由图15可知，腹板开孔后箱型梁结构噪声辐射的峰值频率变为17.5 Hz，较无孔箱型梁有所降低；而在17.5 Hz处腹板开孔的箱型梁噪声辐射声压级较无孔模型20 Hz处的峰值声压有所升高；这与箱型梁腹板开孔导致腹板与翼缘垂向振动及腹板横向振动加剧有关。箱型梁腹板开孔后各场点结构噪声辐射的峰值频率变化如图16所示。

图16　场点噪声峰值频率 Fig.16 Peak frequency of sites sound pressure

4.2场点声压分布云图

图17和图18分别描述了箱型梁腹板无孔与开孔两种工况下跨中横断面场点在峰值频率20 Hz、17.5 Hz处的二维声场分布情况。

从图17所示云图看，腹板无孔箱型梁在20 Hz峰值频率处翼缘垂向振动引发的噪声辐射声压级较高，其次为顶板和底板的垂向振动引发的噪声占主要部分；箱型梁结构噪声辐射沿桥面板水平方向衰减最快，图中表现为声压云图颜色变化较快。

从图18所示云图看，腹板开孔箱型梁远场点在17.5 Hz峰值频率处结构噪声辐射在桥面板以下衰减较慢，行车侧翼缘垂向振动与腹板横向振动引发的噪声辐射声压值较高；腹板开孔箱型梁行车侧结构噪声沿桥面板上方45°方向衰减最快；由于峰值频率降低导致噪声辐射衰减速度降低，图中表现为云图颜色变化较慢。

图17　腹板无孔箱型梁跨中横断面场点声压分布云图(20 Hz)Fig.17 Sound pressure distribution map in middle span of box beam without web hole

图18　腹板开孔箱型梁跨中断面场点声压分布云图(17.5 Hz)Fig.18 Sound pressure distribution map in middle span of box beam with web hole

4.3腹板开孔对箱型梁结构噪声辐射的影响

考虑人耳听阈范围在20Hz以上，箱型梁结构噪声以低频为主，因此通过考虑20～100 Hz频率范围内的声压级来分析腹板开孔对箱型梁结构噪声辐射的影响。图19为20～100 Hz频段各场点线性声压级的最大值。

图19　场点线性声压级最大值Fig.19 The maximum sound pressure

由图19可见，从桥体跨中正下方的场点D1到距桥梁中心线10 m的场点D3，腹板开孔的箱型梁线性声压级最大值降低约3 dB； 在距桥梁中心线20 m的场点D4，其线性声压级最大值升高约1.3 dB，这与腹板开孔措施改变了箱型梁整体结构形态，从而使得腹板与翼缘的振动加强有关；在距桥梁中心线25 m的场点D5，其线性声压级最大值降低约1.3 dB，说明腹板开孔对箱型梁远场点的结构噪声有降低效应。

由图14、15可见，箱型梁结构噪声辐射规律较为复杂，腹板通气孔对箱型梁结构噪声辐射的影响在各频段也不尽相同，因此在分析各场点线性声压级的最大值的基础上，利用声压级叠加原理计算20～100 Hz频段的总体线性声压级，计算结果如图20所示。

图20　场点总体线性声压级Fig.20 Total sound pressure level of sites

由图20可知，腹板开孔措施对箱型梁桥体正下方有较好的降噪效果，这是由于腹板开孔降低顶板和底板的振动水平；在5～10 m近场点无明显降噪效果，在20 m远场点出现声压级的增大，这是由于腹板开孔加强了腹板和翼缘的振动水平；在距桥体中心线25 m处的远场点结构噪声有所降低，说明箱型梁结构噪声辐射水平除了受振动水平控制外，还与传播方向密切相关。

5　结　论

在计算列车荷载作用下箱型梁振动响应的基础上，采用有限元-边界元耦合声学求解方法，计算分析腹板开孔的箱型梁结构噪声辐射特性，并对腹板开孔措施的降噪效果进行了分析。得到如下结论：

(1) 箱型梁结构噪声辐射以0～100 Hz低频为主，振动响应峰值频率20 Hz处线性声压级最大，说明箱型梁噪声辐射水平与振动紧密相关。

(2) 箱型梁腹板开孔能有效降低顶板和底板的振动水平，但同时会加强腹板和翼缘的振动水平；腹板开孔的箱型梁结构噪声沿桥面板上方45°方向衰减最快，衰减方向较腹板无孔时发生较大改变。

(3) 箱型梁腹板开孔措施能够降低桥体正下方的近场点及距桥体中心线25 m外远场点的结构噪声辐射水平，但会在距桥体中心线20 m附近区域有所加强。说明箱型梁结构噪声辐射水平除了受振动水平影响外，还与传播方向密切相关。

低噪声桥梁结构优化设计需要在理论分析和现场试验基础上反复尝试、调整和优化，跨度32 m的混凝土简支箱梁作为我国高速铁路桥梁中使用频率较高的梁型，研究腹板开孔对箱型梁声辐射特性的影响具有重要意义。本文对此进行初步探讨，现场试验及综合降噪措施有待进一步研究。

[1] 刘加华,练松良.城市轨道交通振动与噪声[J].交通运输工程学报,2002(1):29-33.

LIU Jia-hua,LIAN Song-liang.Vibration and noise of the urban rail transit[J].Journal of Traffic and Trans portation Engineering, 2002(1):29-33.

[2] 朱彦,陈光冶,林常明.城市高架轨道桥辐射噪声的计算与分析[J].噪声与振动控制,2005(3):37-41.

ZHU Yan, CHEN Guang-ye, LIN Chang-ming. Numerical prediction and analysis of radiated noise from viaduct of city[J]. Noise and Vibration Control,2005(3):37-41.

[3] 高飞,夏禾,安宁.北京地铁5号线高架结构的辐射噪声分析与实验研究[J].中国铁道科学,2010(5):134-139.

GAO Fei, XIA He, AN Ning. Analysis and experimental study on the radiation noise of the elevated structures of beijing metro line 5 [J].China Rail Way Science,2010(5):134-139.

[4] 江波.城市轨道交通轨道结构噪声分析与减振降噪措施[J].铁道建筑,2004(2):62-65.

JIANG Bo.Analysis of track structure noise of urban rail transit and related reduction measures[J]. Railway Engineering, 2004(2):62-65.

[5] Ngai K W, Ng C F. Structure-noise and vibration of concrete box structure and rail viaduct [J].Journal of Sound and Vibration,2002, 255(2): 281-297.

[6] Janssens M H A, Thompson D J. A calculation model for the noise Irom steel railway bridges [J]. Journal of Sound and Vibration, 1996,193(1):295-305.

[7] 李文会,刘玲玉,谷爱军.轨道交通高架桥梁振动阻抗及传递特性分析[J].都市快轨交通,2013(4): 29-32.

LI Wen-hui, LIU Ling-yu, GU Ai-jun. Analysis on vibration impedance and its transfer characteristics for rail transit viaducts[J]. Urban Rapid Rail Transit, 2013(4): 29-32.

[8] 谢伟平,陈西德,潘支明.空气中钢筋混凝土圆柱壳声辐射特性研究[J].噪声与振动控制,2008,28(3):109-112.

XIE Wei-ping, CHEN Xi-de, PAN Zhi-ming.Analysis of acoustic radiation from reinforced concrete cylindrical shell in air [J].Noise and Vibration Control, 2008,28(3):109-112.

[9] Daneryd A,Nielsen J,Lundberg E,et al.On vibro-acoustic and mechanical properties of perforated railway wheel[C]//Proceedings of the 6th International Workshop on Railway and Tracked Transit System Noise,1998,305-317.

[10] 杨新文,石广田,杨建近.车轮辐板开孔对车轮振动噪声辐射特性的影响[J].中国铁道科学,2014(2):58-64.

YANG Xin-wen,SHI Guang-tian,YANG Jian-jin.Effect of web hole on vibration noise radiation characteristics of railway wheel [J].China Rail Way Science,2014(2):58-64.

[11] 王文栋.混凝土结构构造手册(第四版)[M].北京:中国建筑工业出版社,2012.

[12] 焦映厚,孔霞,蔡云龙,等. 基于FEM和BEM法的大型立式齿轮箱振动噪声计算及测试分析[J]. 振动与冲击,2012,31(4):123-127.

JIAO Ying-hou,KONG Xia,CAI Yun-long,et al.Vibration noise calculation and testing analysis of large vertical planetary transmission gearbox based on FEM and BEM[J].Journal of Vibration and Shock, 2012,31(4):123-127.

[13] 雷晓燕.铁路轨道结构数值分析方法[M].北京:中国铁道出版社,1998.

[14] 刘林芽,吕锐,刘海龙.无砟轨道垂向高频振动响应分析[J].铁道科学与工程学报, 2011,8(6):1-6.

LIU Lin-ya, LÜ Rui, LIU hai-long.Vertical high frequency vibration response analysis of ballastless track[J]. Journal of Railway Science and Engineering, 2011,8(6):1-6.

[15] 李宝银. 高速铁路32 m简支箱梁结构噪声研究[D].北京：中国铁道科学研究院,2014.

[16] 张迅,李小珍,刘全民,等. 高速铁路桥梁结构噪声的全频段预测研究(Ⅱ):试验验证[J]. 铁道学报,2013(2):87-92.

ZHANG Xun, LI Xiao-zhen, LIU Quan-min,et al. Prediction of structure-borne noises of high-speed railway bridges in whole frequency bands(Part Ⅱ):field test verification[J]. Journal of the China Railway Society, 2013(2):87-92.

Structural noise radiation characteristics of box beams with web holes

LIU Linya, XU Daiyan

(Engineering Research Center of Railway Environment Vibration and Noise Ministry of EducationEast China Jiaotong University, Nanchang 330013, China)

Under the action of dynamic loads of trains, box beam structures vibrate and radiate low- frequency noise being harmful to human health. Taking a 32m rail transportation box beam as a study object, the finite element method was adopted to establish two models of the box beam, one with web holes and another without web holes. After calculating the vibration response of the box beam under the action of a train, the structural noise radiation characteristics of the box beam with web holes were analyzed by adopting the finite element-boundary element coupled acoustic solving method. The results showed that web-holes can reduce vertical vibrations of the box beam top and bottom plates; web-holes can change the box beam structural noise attenuation direction and the box beam has a good noise reduction effect below the box beam and at far sites. The study results provided a theoretical reference for the design of urban rail transportation box beams to reduce vibration and noise.

box beam; web hole;low-frequency noise; finite element; boundary element

国家自然科学基金项目(51268014;51578238)；江西省“赣鄱英才555工程”领军人才培养计划项目

2015-05-25修改稿收到日期：2015-08-05

刘林芽 男，教授，博士，博士生导师，1973年生

U491.91；U270.16

A

10.13465/j.cnki.jvs.2016.15.034