Teager能量算子结合MCKD的滚动轴承早期故障识别

刘尚坤， 唐贵基, 何玉灵

(华北电力大学 能源动力与机械工程学院，河北 保定　071003)



Teager能量算子结合MCKD的滚动轴承早期故障识别

刘尚坤， 唐贵基, 何玉灵

(华北电力大学 能源动力与机械工程学院，河北 保定071003)

针对Teager能量算子在解调滚动轴承早期微弱故障特征中的不足，提出一种最大相关峭度解卷积降噪与Teager能量算子解调相结合的滚动轴承早期故障识别方法。首先采用最大相关峭度解卷积算法以包络谱的峭度最大化为目标对原信号进行降噪处理、检测信号中的周期性冲击成分，然后利用Teager能量算子增强降噪信号中的周期性冲击特征、抑制非冲击成分，最后通过分析Teager能量谱中明显的频率成分来诊断故障类型。滚动轴承外圈、内圈故障诊断实例表明，该方法能有效实现滚动轴承早期微弱故障的识别。

Teager能量算子；最大相关峭度解卷积；滚动轴承；早期故障诊断

当滚动轴承组成元件发生故障时，如内圈、外圈、滚动体表面的点蚀、裂纹和剥落等，这些局部损伤点与其它元件反复接触，会产生周期性冲击信号，但故障早期冲击信号微弱，又由于实际中振动传输路径复杂、噪声干扰严重、多振动源激励和响应互相耦合等诸多因素影响，使得滚动轴承早期故障诊断相对困难，探寻行之有效的微弱故障特征提取方法一直是故障诊断领域的热点和难点[1]。

Teager能量算子是一种非线性差分算子，由于具有时间分辨率高，解调速度快的优点，近些年被广泛用于信号解调分析[2-5]。王天金等[3]利用Teager能量算子突出滚动轴承故障振动信号中的冲击特征，并用频谱特征识别故障特征频率；张文义等[4]采用能量算子解调方法对共振稀疏分解分离出的滚动轴承冲击成分进行解调，诊断了滚动轴承故障，但两者没有探讨方法对早期故障的适用性。杨青乐等[5]在角域中利用Teager能量算子增强信号中的冲击成分，结合倒阶次谱实现了变速器加速过程中滚动轴承的微弱故障诊断，角域中的倒阶次谱对应时域中的倒谱，本文研究发现该方法在分析时域中信噪比较低的恒定转速振动信号时，效果不明显，这是由于Teager能量算子解调方法只适用于单分量的调幅调频信号(AM-FM信号)解调[6]，而旋转机械运行时振动信号中往往含有与转频相关的其它分量和强噪声成分，而MCKD作为一种新的降噪方法能对指定周期的冲击成分进行检测。本文提出以包络谱的峭度最大化为目标选取MCKD降噪的优化参数，对原信号进行预处理，然后用Teager能量算子增强降噪信号中的周期性冲击成分，进一步通过分析Teager能量谱中的故障特征频率来实现滚动轴承早期故障识别。

1　Teager能量算子

Teager能量算子通过信号的瞬时值及其微分的非线性组合来估计信号源产生动态信号所需的总能量，能够增强信号的瞬态特征[6-7]。对于调幅调频信号x(t)=a(t)cos[φ(t)]，对应能量算子定义为

(1)

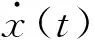
ψ[x(t)]=[a(t)φ′(t)]2+a2(t)φ″(t)×

sin[2φ(t)]/2+cos2[φ(t)]ψ[a(t)]

(2)

由于通常调制信号比载波信号变化慢的多，所以其幅频值可近似视为常数处理[8]，即ψ[a(t)]≈0，φ″(t)≈0，则有

ψ[x(t)]≈[a(t)φ′(t)]2=a2(t)ω2(t)

(3)

同理可得

ψ[x′(t)]≈a2(t)ω4(t)

(4)

计算x(t)的瞬时幅值和瞬时相位分别为

(5)

(6)

由式(3)知，Teager能量算子的输出较传统能量计算增大了频率平方的倍数，使得Teager能量算子能有效增强瞬态冲击成分。分析其瞬时幅值的频谱可以判断是否存在故障特征频率，实现故障诊断。

2　MCKD算法及其参数选择

2.1MCKD算法

最大相关峭度解卷积算法(MCKD)[9]实质是以相关峭度为评价指标，通过解卷积运算，突出信号中被噪声掩盖的周期脉冲成分，本文将其用于滚动轴承早期微弱故障诊断中的降噪及检测周期冲击成分。

周期信号y的相关峭度表达式为

(7)

式中：T为冲击信号的周期；M为移位数。

相关峭度充分考虑了冲击成分的连续性，能准确的衡量信号中周期性脉冲。MCKD算法以相关峭度最大化为目标函数，即：

(8)

式中：f=[f1f2…fL]T为长度为L的滤波器系数。

求解过程等价于求解方程

k=1,2,…,L

(9)

求得的结果以矩阵的形式表述为

(10)

式中：

r=[0T2T3T4T…mT]；

MCKD迭代求解f的过程为：

(1) 选择滤波器L、周期T、移位数M；

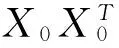
(3) 计算滤波后的输出信号y(n)；

(4) 由y(n)计算αm与β；

(5) 更新滤波器系数f；

(6) 如果滤波前后信号的ΔCKM(T)小于给定阈值，则停止迭代，否则返回步骤(3)。

2.2MCKD参数选择

虽然MCKD算法可以在信噪比很低的情况下检测信号中的周期冲击成分、抑制信号中的噪声，实现信号降噪并提升原信号的峭度[10]，然而参数不同其降噪效果存在明显差异，MCKD算法的主要影响参数有滤波器长度L、冲击信号周期T、移位数M等。待检测的冲击信号周期T可以通过理论计算得到；移位数M一般取1～7，M值越大，解卷积结果中连续脉冲的个数会越多，但需要对冲击信号周期估计更准确，同时也会增加计算的运算量，而实际故障频率往往与理论故障频率略有差异，故本文取M=5；滤波器长度L是非常关键的参数，本文滤波器长度L的最优值取10～500中使得原信号处理后包络谱的峭度最大的L值。

峭度对冲击性特别敏感，峭度值越大说明冲击成分所占的比重越多[11]，如果包络谱中故障频率突出，则包络谱的峭度值比较大，因此，本文提出以包络谱的峭度来衡量原信号经MCKD降噪的效果，即对不同L值降噪后的信号求其包络谱的峭度，取峭度值最大时对应的滤波器长度为最优值，对原信号进行降噪处理。

以下是本文实现故障识别的主要步骤：

(1) 设定MCKD算法中故障冲击周期T，移位数M，以包络谱的峭度最大化为目标，搜索滤波器长度L并确定最优值；

(2) 以优化参数的MCKD算法对原信号进行降噪处理；

(3) 采用Teager能量算子增强降噪信号中的瞬态冲击成分，抑制非冲击成分；

(4) 对处理后的信号进行Fourier频谱分析，依据Teager能量谱中突出的频率成分诊断故障类型。

3　实测信号分析

3.1滚动轴承外圈故障分析

选取美国辛辛那提智能维护中心的滚动轴承全寿命实验数据进行分析[12]。试验台布置如图1所示。实验转轴上装有4个相同的轴承，由交流电动机通过皮带牵引。同时通过弹性系统给转轴和轴承施加约26 671 N的径向载荷。每个轴承的水平和垂直方向各布置一个加速度传感器，采用NI公司生产的6062E型采集卡进行采集数据。滚动轴承参数见表1。

图1　实验台示意图Fig.1 Schematic diagram of experiment platform

型号轴承节径滚动体直径滚动体个数接触角ZA211571.5mm8.4mm1615.17°

本文选用该实验的第2次测试数据，实验结束时，轴承1出现外圈磨损失效，实验持续了164 h，数据采集间隔为10min，每次采集20 480个点，共采集984个文件，采样频率fs=20 kHz。图2为轴承1垂直方向传感器采得的各个文件数据均方根值Xrms的趋势图。在7 020 min时轴承振动信号的均方根值出现明显波动，表明轴承出现故障。但均方根值对早期故障并不敏感。

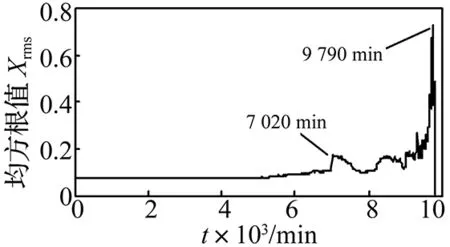
图2　轴承1垂直方向振动信号均方根值趋势图Fig.2 Xrms trend for vertical vibration signal of bearing 1

图3　t=5 310 min时刻振动信号的时域波形和包络谱Fig.3 Signal time domain waveform and envelope spectra at t=5 310 min

图4　Teager能量解调信号的频谱和倒谱Fig.4 Spectra and cepstrum of Teager energy operator demodulation

为验证本文方法对滚动轴承早期故障特征提取的有效性，选取5 310 min时的轴承振动数据作为分析对象, 取10 000个数据点，该时刻轴承转轴实际转速为1 948 r/min，计算得外圈故障特征频率fo=230 Hz，图3(a)、(b)分别为此时振动信号的时域波形和包络谱，包络谱图中轴承外圈故障特征频率无法识别。再采用文献5所述方法进行分析，图4(a)、(b)分别为采用Teager能量算子解调后的Fourier频谱和倒谱分析结果，由图可知频谱和倒谱中均没有出现明显峰值，不能识别故障特征频率。采用本文方法进行分析，图5(a)、(b)分别为振动信号经参数优化的MCKD(L=374，最大峭度值为13.175 1)降噪后的时域波形和包络谱，包络谱中外圈故障频率fo=230 Hz处峰值突出，倍频成分略有体现但幅值较小。图6为降噪信号经Teager能量算子解调后的频谱图，可见外圈故障特征频率及其倍频fo～4fo处谱峰突出，表明轴承外圈发生故障，与实际情况相符，与均方根值指标相比可提前 1 710 min 诊断出轴承故障。对比图4(a)、(b)分析结果说明本文方法的有效性。

图5　MCKD降噪信号的时域波形和包络谱Fig.5 Time domain waveform and envelope spectrum of MCKD de-nosed signal

图6　降噪信号经Teager能量算子解调的频谱Fig.6 Teager energy operator demodulation spectra of de-nosed signal

为检验本文方法再选取510 min时的正常轴承振动数据进行分析，图7为经MCKD降噪、Teager能量解调后的频谱，图中未发现异常特征频率，与轴承实际正常工作状态相符。

图7　t=510 min时刻正常振动信号分析Fig.7 Analysis of normal signal at t=510 min

3.2滚动轴承内圈故障分析

滚动轴承内圈故障振动信号来自美国西储大学电气工程实验室。实验轴承驱动端型号为SKF6205，具体参数如表2所示，内圈损伤为电火花加工的单点损伤，故障点直径为0.355 6 mm，采样频率fs=12 kHz，电机轴转频fr=28.8 Hz。计算得滚动轴承内圈故障特征频率fi=156 Hz。选取6 000个故障数据点作为分析对象。图8(a)、(b)分别为内圈故障信号的时域波形和包络谱，受干扰成分影响包络谱中只有转频fr峰值明显，内圈故障特征频率无法识别，诊断失败。

表2　SKF6205轴承基本参数

图8　内圈故障信号的时域波形和包络谱Fig.8 Time domain waveform and envelope spectrum of inner race fault signal

图9　Teager能量算子解调信号的频谱和倒谱Fig.9 Spectra and cepstrum of Teager energy operator demodulation

采用文献[5]所述方法进行分析，图9(a)、(b)分别为采用Teager能量算子解调后的频谱和倒谱分析结果，频谱图中转频fr峰值明显，虽有内圈故障频率fi，但幅值相对较小，容易漏诊，倒谱分析图中没有明显的倒频率1/156=0.006 4 s，不能识别内圈故障特征。采用本文方法进行分析，图10(a)、(b)分别为振动信号经参数优化的MCKD(L=245，最大峭度值为23.554 1)降噪后的时域波形和包络谱，包络谱中内圈故障频率fi=156 Hz处出现峰值，其它倍频幅值较小体现不明显。图11为降噪信号经Teager能量算子解调后的频谱，由图可知，故障频率及其倍频1～6fi处出现明显谱峰，并且内圈故障特征频率被转频调制的边频带也有所体现。对比图9(a)、(b)分析结果说明本文方法效果明显。

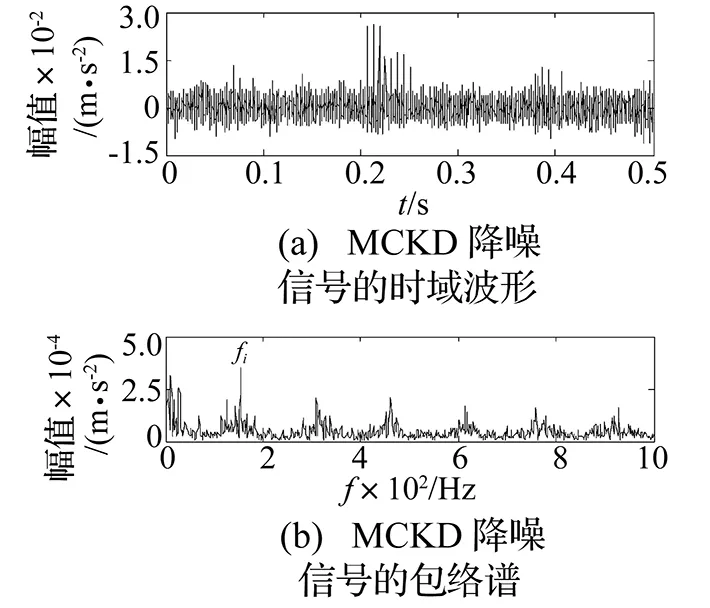
图10　MCKD降噪信号的时域波形和包络谱Fig.10 Time domain waveform and envelope spectra of MCKD de-nosed signal

图11　降噪信号经Teager能量算子解调的频谱Fig.11 Teager energy operator demodulation spectra of de-nosed signal

4　结　论

(1) 滚动轴承早期故障的诊断对设备正常运行有着重要的意义，但早期故障时，故障冲击特征微弱通常被其它成分淹没，采用包络谱分析或Teager能量算子解调分析可能会失效。

(2) 先采用参数优化的MCKD算法对振动信号进行预处理，再用Teager能量算子增强冲击成分，并结合频谱分析能有效实现滚动轴承早期微弱故障诊断。

(3) 分析方法对变转速过程中滚动轴承的早期故障诊断方法有一定借鉴意义。

[1] 雷亚国，韩冬，林京，等．自适应随机共振新方法及其在故障诊断过程中的应用[J]．机械工程学报，2012，48(7)：62-67．

LEI Ya-guo，HAN Dong，LIN Jing，et al．New adaptive stochastic resonance method and its application to fault diagnosis[J]．Journal of Mechanical Engineering，2012，48(7)：62-67．

[2] Cheng J，Yu D，Yang Y．The application of energy operator demodulation approach based on EMD in machinery fault diagnosis[J]．Mechanical Systems and Signal Processing，2007，21(2)：668-677．

[3] 王天金，冯志鹏，郝如江，等．基于Teager能量算子的滚动轴承故障诊断研究[J]．振动与冲击，2012，31(2)：1-5．

WANG Tian-jin，FENG Zhi-peng，HAO Ru-jiang，et al．Fault diagnosis of rolling element bearings based on teager energy operator[J]．Journal of Vibration and Shock，2012，31(2)：1-5．

[4] 张文义，于德介，陈向民．基于信号共振稀疏分解与能量算子解调的轴承故障诊断方法[J]．中国电机工程学报，2013，33(20)：111-118．

ZHANG Wen-yi，YU De-jie，CHEN Xiang-min．Fault diagnosis of rollingbearings based on resonance-based sparse signal decomposition and energy operator demodulating [J]．Proceedings of the CSEE，2013，33(20)：111-118．

[5] 杨青乐，梅检民，肖静，等．Teager能量算子增强倒阶次谱提取轴承微弱故障特征[J]．振动与冲击，2015，34(6)：1-5．

YANG Qing-le，MEI Jian-min，XIAO Jing，et al．Weak fault feature extraction for bearing based on order cepstrum enhanced by teager energy operator[J]．Journal of Vibration and Shock，2015，34(6)：1-5．

[6] Marago S P，Kaiser J F，Quatieri T F．Energy separation in signal modulations with applications to speech analysis [J] ．IEEE Transactions on Signal Processing，1993，41(10)：3024-3051．

[7] 程军圣，杨怡，杨宇．基于LMD的能量算子解调机械故障诊断方法[J]．振动、测试与诊断，2012，32(6)：915-919．

CHENG Jun-sheng，YANG Yi，YANG Yu．Mechanical fault diagnosis of energy operator demodulating approach based on LMD[J]．Journal of Vibration，Measurement & Diagnosis，2012，32(6)：915-919．

[8] 鞠萍华，秦树人，赵玲．基于LMD的能量算子解调方法及其在故障特征信号提取中的应用[J]．振动与冲击，2011，30(2)：1-4．

JU Ping-hua，QIN Shu-ren，ZHAO lin．Energy operator demodulating approach based on LMD and its application in extracting the fault characteristics of signal[J]．Journal of Vibration and Shock，2011，30(2)： 1-4．

[9] Mcdonald G L，Zhao Q，Zuo M J．Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection[J]．Mechanical Systems and Signal Processing，2012，33：237-255．

[10] 武兵，贾峰，熊晓燕．基于最大相关峭度反褶积的轴承故障诊断方法[J]．振动、测试与诊断，2014，34(3)：570-575．

WU Bing，JIA Feng，XIONG Xiao-yan．Bearing fault diagnosis based on maximum correlated kurtosis deconvolution [J]．Journal of Vibration，Measurement & Diagnosis，2014，34(3)：570-575．

[11] 胡爱军，马万里，唐贵基．基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J]．中国电机工程学报，2012，32(11)：106-111．

HU Ai-jun，MA Wan-li，TANG Gui-ji．Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]．Proceedings of the CSEE，2012，32(11)：106-111．

[12] Qiu H，Lee J，Lin J，et al．Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J]．Journal of Sound and Vibration，2006，289(4/5)：1066-1090．

Incipient fault diagnosis of rolling bearings based on Teager energy operator and MCKD

LIU Shangkun, TANG Guiji, HE Yuling

(School of Energy, Power and Mechanical Engineering，North China Electric Power University, Baoding 071003, China)

Aiming at Teager energy operator’s insufficient in demodulating rolling bearings’ incipient weak fault features, a diagnosis method combining the maximum correlated kurtosis deconvolution(MCKD) and Teager energy operator was proposed. Firstly, an original signal was de-noised with MCKD algorithm, and the max kurtosis of its envelope spectrum was taken as an objective to detect its periodic impact components. Then, periodic impact components were enhanced and non impact components were suppressed using Teager energy operator. At last, fault types were diagnosed by analyzing obvious frequency components in Teager energy spectrum. Analysis results of rolling bearings’ outer ring faults and inner ring faults showed that this method can identify the incipient weak faults of rolling bearings effectively.

Teager energy operator; maximum correlated kurtosis deconvolution(MCKD); rolling bearing; incipient fault diagnosis

国家自然科学基金(51307058)；河北省自然科学基金(E2014502052;E2015502013)；中央高校基本科研业务费专项资金资助(2014MS156;2015ZD27)

2015-05-11修改稿收到日期：2015-07-13

刘尚坤 男，博士生，讲师，1979年生

TH165; TH133

A

10.13465/j.cnki.jvs.2016.15.016