噪声非线性效应的增强与弱涡街信号检测方法

唐迅捷， 林　敏， 黄咏梅

(中国计量学院 计量测试工程学院，杭州　310018)



噪声非线性效应的增强与弱涡街信号检测方法

唐迅捷， 林敏， 黄咏梅

(中国计量学院 计量测试工程学院，杭州310018)

噪声与非线性势场相互作用产生的效应能够助长微弱信号。针对小流量产生的涡街信号较弱而难以检测的问题，从增强噪声非线性效应的角度出发，比较了不同非线性形式势函数下的噪声效应，构造了对称抛物线势函数。理论分析和数值仿真结果表明具有对称抛物线势函数的系统输出有较高的信噪比。提出了一种利用对称抛物线系统增强噪声效应的检测弱涡街信号方法，实测弱涡街信号检测结果表明该方法能有效获取小流量涡街信号的特征频率。

噪声；非线性；增强效应；弱涡街信号检测；对称抛物线势函数

涡街流量计是一种流体振动型流量计，由于流体的流速与其振动频率成正比，准确检测出流体的振动频率是涡街流量计应用的关键。而实际应用中管道及设备的振动会产生噪声的干扰[1]，因此涡街流量计的输出信号不仅包括流速产生的涡街信号，还包括干扰引起的噪声信号，这时涡街信号往往会被噪声淹没而难以检测。常规的信号处理方法[2-5]是从“消灭”噪声的角度出发，采用去除噪声或降低噪声的途径来提取有用信号，但在削弱噪声的同时，也减弱了涡街信号。特别是小流量产生的弱涡街信号极易受到噪声的干扰，输出信噪比极低，涡街信号的特征频率难以提取[6-7]。

打破噪声有害的传统观念，在非线性条件下噪声能起到助长微弱信号，提高输出信噪比的作用[8-10]，存在着噪声的非线性效应，而这个效应的强弱与非线性的具体形式有关。研究噪声效应最常用的非线性形式是经典双稳势函数，但该势函数的饱和特性限制了噪声非线性效应的增强。因此，基于噪声与非线性势场的相互作用，研究噪声对非线性的敏感性及噪声效应的增强具有潜在的应用价值。

增强信噪比极低的弱涡街信号中噪声的非线性效应，是实现弱涡街信号检测的关键。从增强效应[11]的角度出发，以kramers逃逸率和信噪比大小作为衡量噪声效应强弱的指标，分析比较了分段混合势函数[12]和分段线性势函数[13]下噪声非线性效应的强弱。进一步改变势函数的形式，构造了对称抛物线势函数，理论分析和数值仿真结果表明对称抛物线势场与噪声相互作用产生的非线性效应较强烈，能有效提高系统的输出信噪比。最后，利用噪声非线性效应的增强对强噪声背景下实测小流量产生的弱涡街信号进行检测。

1　噪声的非线性效应

非线性条件下，由周期信号和噪声的合作使得系统输出信噪比增强的现象为噪声的非线性效应，研究噪声非线性效应的模型可由以下方程表示

(1)

式中:U(x)是非线性势函数，Acos(2πf0t)是外界作用到系统中的微弱周期信号。η(t)是满足〈η(t)〉=0，〈η(t)η(t′)〉=2Dδ(t-t′)的高斯白噪声，其中D为噪声强度。

由于经典双稳势函数中四次方函数形式的存在，系统输入输出之间有一种饱和关系，因此信噪比难以提高。而分段混合势函数和分段线性势函数能够克服这种饱和特性，在一定程度上增强了噪声的非线性效应，使得系统具有较高的信噪比。因此，改变势函数的非线性形式能够影响噪声效应的强弱。本文以增强噪声的非线性效应为目的，构造了对称抛物线势函数，其表达式为

(2)

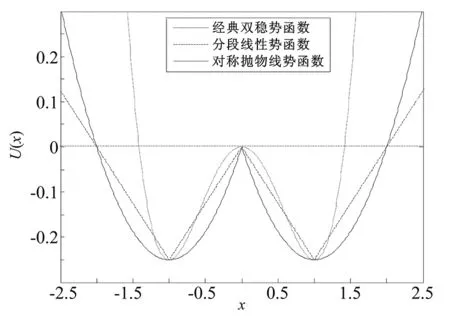
图1　不同非线性形式的势函数曲线Fig.1 The different nonlinear form of the potential function

2　噪声非线性效应的增强

2.1势函数的非线性与增强效应

采用信噪比度量噪声非线性效应的强弱，相同周期信号和噪声作用下，不同非线性系统的输出信噪比大小与Kramers逃逸率有关。Kramers逃逸率越大，粒子在两势阱间跃迁的速度越快，系统对噪声越敏感，从而更容易激发出噪声的低频能量，提高输出信噪比，使得噪声的非线性效应得到增强。

令R-和R+分别表示粒子从左右势阱底部出发的逃逸率，势函数为U(x)的双稳类系统具有的Kramers逃逸率[14]为

(3)

从式(3)可以看出，噪声一定的条件下，不同系统的Kramers逃逸率大小由势函数的非线性形式决定。因此，从势函数的非线性形式出发，分析Kramers逃逸率的大小，进而找到增强噪声非线性效应的方法。

将式(2)中的U(x)代入式(3)，当参数D≪1时,近似得到对称抛物线系统的Kramers逃逸率为

(4)

当μ=1时，不同非线性系统的Kramers逃逸率随噪声强度的变化曲线如图2所示。

图2　Kramers逃逸率随噪声强度的变化Fig.2 Kramers escape rate along with the change of noise intensity

图2中Kramers逃逸率的大小体现了噪声非线性效应的强弱，相同噪声强度作用下，对称抛物线系统的Kramers逃逸率较大，噪声的非线性效应较强烈，分段线性系统的Kramers逃逸率次之。

系统输出信噪比[15]为

(5)

(6)

输入信号幅值A=0.3，系统参数μ=1，输出信噪比随噪声强度变化的理论曲线如图3所示。噪声强度由小到大的变化过程中，两种不同非线性系统的信噪比均表现出了单峰特性，峰值的高低体现了噪声不同强弱程度的非线性效应。图3中对称抛物线系统的信噪比峰值较高，表明噪声在该系统中的效应较强烈，从而能够有效检测微弱信号。

图3　输出信噪比随噪声强度D变化的理论曲线Fig.3 The theoretical output SNR along with the change of noise intensity D

采用四阶龙格库塔算法，相同周期信号和噪声作用下，选取系统参数μ=1，对分段线性系统和对称抛物线系统的噪声非线性效应进行数值仿真。输入微弱周期信号幅值A=0.3，频率为f0=0.01 Hz，采样频率fs=5 Hz。不同非线性系统输出信噪比随噪声强度变化的曲线如图4所示，对称抛物线系统具有较高的输出信噪比，噪声的非线性效应较强烈，数值仿真结果与理论分析基本一致。

图4　输出信噪比随噪声强度D变化的仿真曲线Fig.4 The emulational output SNR along with the change of noise intensity D

2.2势场力与Kramers逃逸率

(7)

图5　不同势场力随位移变化曲线Fig.5 The different potential field force along with the change of displacement

势场力随位移的变化曲线由非线性势函数的形式决定，如图5所示。分段线性系统的势场力是常数力，单一势阱内，以势阱底部为突变点， 势阱两侧的势场力大小相等，方向相反。对称抛物线系统的势场力如图5中两条斜线所示，该力在单一势阱内是随位移变化的线性力，以势场力为0的势阱底部位置为中心点，力的方向相反，大小与位移成正比。由于对称抛物线系统的Kramers逃逸率较大，这表明线性力更有利于增强噪声的非线性效应。

3　弱涡街信号的检测结果与分析

实验采用口径为50 mm的1.0级应力式涡街流量计，以精度为0.2级的电磁流量计测得值作为实验管道的标准流量值。涡街流量检测实验装置的示意图如图6所示。

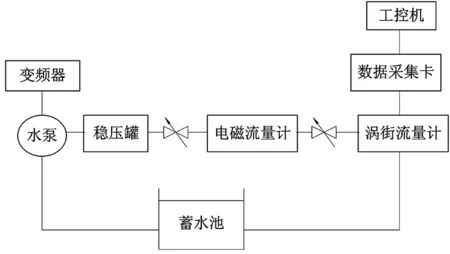
图6　涡街流量检测实验装置示意图Fig.6 The vortex flow test device

如图6是一个循环的水管路，由变频器控制水泵促使系统内的水介质流动，经过稳压罐后的水流入电磁流量计和涡街流量计，最后流回蓄水池。

实验采集小流量产生的弱涡街信号进行分析，首先对涡街流量计输出的原始信号进行二次采样预处理[16]，然后利用噪声与非线性势场相互作用的效应检测涡街信号的特征频率，最后对输出信号进行尺度恢复。由于经典双稳系统中噪声的非线性效应较弱，涡街信号特征频率处的功率谱值仍然淹没在噪声中无法判别。改变系统非线性的形式，利用噪声效应的增强，实现对弱涡街信号的检测。

3.1流速为4.01 m3/h的涡街信号检测

采集流速为4.01 m3/h的小流量涡街信号进行分析。设置采样频率fs=5 000 Hz，采样点数N=15 498，图7是涡街信号的时域图和功率谱图，由于噪声的干扰较大，无法直接从图7中分辨出涡街信号特征频率。

图7　4.01 m3/h时涡街信号时域图和功率谱图Fig.7 The time domain waveform and power spectrum of vortex signal under 4.01 m3/h

选取系统参数μ=0.2，设置二次采样压缩比R=2 000，经过不同非线性系统处理后再进行尺度恢复。图8(a)是通过分段线性系统处理后的输出信号功率谱图，此时涡街信号的特征频率仍然被噪声淹没，无法提取。图8(b)是经过对称抛物线系统处理后的输出信号功率谱图，其中功率谱最高峰对应的频率即为特征频率fr=0.005 035 Hz，此时特征频率处的谱峰值增加到了0.008 319，且谱值变得很突出，可准确检测出涡街信号的特征频率。经尺度还原后得到原始涡街信号的频率fd=fr·R=10.07 Hz。而4.01 m3/h时的涡街频率理论值为10.30 Hz。说明对称抛物线系统中噪声的非线性效应较强烈，从而能够有效地检测涡街信号的特征频率。

图8　分段线性系统和对称抛物线系统输出功率谱图Fig.8 The output power spectrum of piecewise linear system and symmetrically parabolic system

3.2流速为2.49 m3/h的涡街信号检测

进一步采集流速更小的涡街信号进行分析。设置采样频率fs=5 000，采样点数N=15 010，系统参数μ=0.2，二次采样压缩比R=2 500。图9是2.49 m3/h时涡街流量信号时域图及功率谱图，涡街信号已完全被噪声淹没，无法直接从功率谱图中分辨出涡街信号的特征频率。

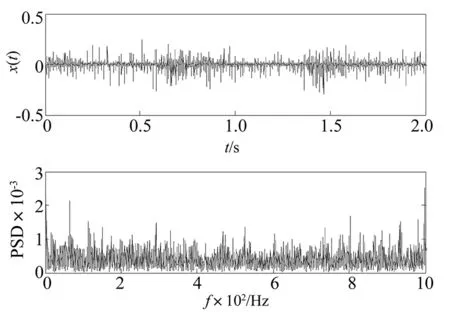
图9　2.49 m3/h时涡街信号时域图及功率谱图Fig.9 The time domain waveform and power spectrum of vortex signal under 2.49 m3/h

图10　分段线性系统和对称抛物线系统输出功率谱图Fig.10 The output power spectrum of piecewise linear system and symmetrically parabolic system

流体的流速越小，产生的涡街信号越弱，越难以检测。因此，需要增强弱涡街信号中噪声的非线性效应来提取特征频率。该小流量涡街信号经过不同非线性系统处理后，输出信号的频谱结构发生了变化，能量大部分集中在中低频区域，系统的输出功率谱图如图10所示。图10(a)是经分段线性系统处理后输出信号的功率谱图，其中涡街信号特征频率仍然被淹没，无法提取，表明涡街信号的噪声在分段线性系统中的非线性效应较弱。图10(b)是经对称抛物线系统处理后输出信号的功率谱图，峰值最高点对应的涡街信号特征频率为fr=0.002 497 Hz。经过尺度恢复后，待测的涡街信号特征频率fd=fr·R=6.24 Hz，而2.49 m3/h时涡街信号的频率理论值为6.30 Hz。因此，对于更小流量的涡街信号，对称抛物线系统仍可利用噪声非线性效应的增强准确有效地提取弱涡街信号的特征频率。

4　结　论

利用非线性势场与噪声相互作用的效应能够提取被噪声淹没的微弱信号。不同非线性系统对噪声的响应能力是有差异的，从而决定了噪声的非线性效应有强有弱。针对强噪声背景下无法提取弱涡街信号的情况，提出了能增强噪声效应的对称抛物线势函数，理论分析和数值仿真结果表明对称抛物线系统具有较高的输出信噪比。实测弱涡街信号的检测结果表明，对称抛物线系统对弱涡街信号中的噪声干扰较敏感，利用噪声非线性增强效应能有效提高涡街信号频率处的功率谱值，从而可以准确地获取特征频率，实现涡街信号的检测。这为提高涡街流量计现场适应性及弱涡街信号的检测提供了一种新的信号处理方法。

[1] 邢娟, 张涛, 郝松. 管道振动对涡街流量计测量影响的试验研究[J]. 振动与冲击, 2009, 28(3): 112-115.

XING Juan, ZHANG Tao, HAO Song. Experimental research on measuring accuracy of vortex flowmeter under pipe vibrations[J].Journal of Vibration and Shock,2009,28(3):112-115.

[2] 江文斌, 秦会斌, 邵李焕,等. 基于经典谱估计改进方法的涡街流量计[J]. 仪器仪表学报, 2012, 33(1): 229-234.

JIANG Wen-bin, QIN Hui-bin, SHAO Li-huan, et al. Vortex flowmeter based on improved classical spectral estimation[J]. Chinese Journal of Scientific Instrument, 2012,33(1):229-234.

[3] 邰永红, 沈天飞, 李诚. 小波滤波法在涡街流量计中的应用[J]. 电子测量技术, 2011, 34(11): 101-103.

TAI Yong-hong, SHEN Tian-fei, LI Cheng. Application on wavelet filter in vortex flowmeter[J]. Electronic Measurement Technology, 2011, 34(11): 101-103.

[4] 黄云志, 徐科军. 基于IIR小波滤波器的涡街流量计数字信号处理系统[J].仪器仪表学报, 2007, 28(12): 2142-2146.

HUANG Yun-zhi, XU Ke-jun. Digital signal processing system based on IIR wavelet filter for vortex flowmeter[J]. Chinese Journal of Scientific Instrument, 2007, 28(12): 2142-2146.

[5] 郑德智, 王帅, 樊尚春. 涡街流量传感器信号处理方法研究[J]. 传感技术学报, 2009, 22(1): 80-84.

ZHENG De-zhi, WANG Shuai, FAN Shang-chun. Research on signal processing method of vortex flowmeter [J].Chinese Journal of Sensors and Actuators, 2009, 22(1): 80-84.

[6] 邢娟, 张涛. 利用涡街流量计测量油水两相流流量[J]. 仪器仪表学报, 2009, 30(4): 882-886.

XING Juan, ZHANG Tao. oil-water two-phase flow measurement using vortex flowmeter[J]. Chinese Journal of Scientific Instrument, 2009, 30(4): 882-886.

[7] 罗清林, 徐科军, 刘三山.基于快速傅里叶变换的低功耗两线制涡街流量计[J]. 电子测量与仪器学报,2010,24(7):692-697.

LUO Qing-lin, XU Ke-jun, LIU San-shan. Vortex flowmeter with low power and two-wires based on FFT [J].Journal of Electronic Measurement and Instrument,2010,24(7):692-697.

[8] 郝研, 王太勇, 万剑,等. 基于级联双稳随机共振和多重分形的机械故障诊断方法研究[J]. 振动与冲击, 2012, 31(8): 181-185.

HAO Yan, WANG Tai-yong, WAN Jian, et al. Mechanical fault diagnosis based on cascaded biatable stochastic resonance and multi-fractal [J]. Journal of Vibration and Shock, 2012, 31(8)：181-185.

[9] 夏均忠, 刘远宏, 马宗坡,等.基于调制随机共振的微弱信号检测研究[J]. 振动与冲击, 2012, 31(3): 132-135.

XIA Jun-zhong，LIU Yuan-hong，MA Zong-po,et al. Research on weak signal detection based on the modulated stochastic resonance [J].Journal of Vibration and Shock, 2012,31(3):132-135.

[10] 林敏, 黄咏梅. 基于振动共振的随机共振控制[J]. 物理学报, 2007, 56(11): 6173-6177.

LIN Min, HUANG Yong-mei. Stochastic resonance control based on vibration resonance[J]. Acta Phys. Sin., 2007, 56(11): 6173-6177.

[11] 梁忠诚，赵瑞.磁致旋光增强效应与微量样品旋光检测方法[J]. 光学学报, 2009，29(8): 2221-2224.

LIANG Zhong-cheng, ZHAO Rui.Effect of magneto-optic rotation enhancement and the polarimetric detection of the small rotation angles[J].Acta Optica Sinica, 2009, 29(8): 2221-2224.

[12] Zhao W L,Wang J, Wang L Z,Chaos 23, 2013, 033117.

[13] 王林泽, 赵文礼, 陈旋. 基于随机共振原理的分段线性模型的理论分析与实验研究[J]. 物理学报, 2012, 61(16): 160501.

WANG Lin-ze, ZHAO Wen-li, CHEN Xuan. Theory and experiment research on a Piecewise-linear model based on stochastic resonance[J]. Acta Phys. Sin., 2012,61(16):160501.

[14] 胡岗.随机力与非线性系统[M].上海:上海科技出版社,1994.

[15] Gammaitoni L, Hanggi P, Jung P,et al. Stochastic resonance[J]. Rev. Mod. Phys, 1998, 70(1): 223-285.

[16] 冷永刚, 王太勇. 二次采样用于随机共振从强噪声中提取弱信号的数值研究[J]. 物理学报, 2003, 52(10): 2432-2437.

LENG Yong-gang, WANG Tai-yong. Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy Noise[J]. Acta Phys. Sin., 2003, 52(10): 2432-2437.

Enhanced noise nonlinear effects and detection method of weak vortex signals

TANG Xunjie, LIN Min, HUANG Yongmei

(College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China)

The effects generated by interaction of noise and nonlinear potential field can enhance weak signals. Aiming at the problem that weak vortex signals generated by low flowrate were difficult to detect, from the viewpoint of enhancing noise nonlinear effects, the noise effects of different nonlinear potential functions were compared, a symmetric parabolic potential function was constructed. The theoretical analysis and numerical simulation indicated that a system with the symmetric parabolic potential function has a higher SNR. A method to detect weak vortex signals was proposed with a symmetric parabolic system to enhance noise effects. The detection results of real vortex signals indicated that this method can effectively get characteristic frequencies of low flow-rate vortex signals.

noise; nonlinear; enhanced effects; weak vortex signal detection; symmetric parabolic potential function

浙江省自然科学基金(LY13E050012)

2015-06-08修改稿收到日期：2015-08-14

唐迅捷 女，硕士生，1991年3月生

林敏 男，硕士，教授，硕士生导师，1962年9月生

TH113

A

10.13465/j.cnki.jvs.2016.15.028