充水密加筋夹层结构固有特性仿真及试验研究

武大江， 梅志远， 王永历

(海军工程大学 舰船工程系，武汉　430000)



充水密加筋夹层结构固有特性仿真及试验研究

武大江， 梅志远， 王永历

(海军工程大学 舰船工程系，武汉430000)

针对充水密加筋夹层结构,考虑内域流固耦合模态计算时出现的计算量过大的问题，提出了基于ABAQUS的附加质量替代方法，并通过对不同半径和高度的充水圆柱壳模型的分析，探讨了附加质量方法的适用性问题。同时，为了更直观地评价内域耦合湿模态计算过程中流体对结构固有频率的影响，引入了流体参与度的概念，并指出针对内域耦合问题，流体参与度系数取值在1附近时，附加质量替代方法有较高的计算精度。最后，采用附加质量方法对加筋夹层结构充水模态进行计算，并与试验值对比，验证了方法的正确性。

附加质量法；流固耦合；加筋夹层结构；有限元法

舰艇和水下平台的附体结构通常设计成非耐压形式，其在水下工作时结构内部充满水，这部分水随结构一起振动，改变了结构的振动特性。而一般探讨结构水下振动特性时往往只考虑外域和结构的流固耦合作用，对内域的研究相对较少。相对于外域耦合而言，内域耦合受流体边界条件和结构外形影响较小，而受结构内部的储液特性影响较大。

工程上对内域与结构耦合问题的研究多分成两类：存在自由液面的情况，如大型储液罐[1]，液舱振动[2]等；不存在自由液面的情况，如潜艇双层柱壳[3]充液管路[4]等。研究方法有单向耦合和双向流固耦合之分[5]。单向流固耦合研究在假设结构为刚体的前提下，得出附加质量的分布情况，然后分析结构的振动特性；考虑双向流固耦合，多从流体动压力出发，推导出附加质量矩阵，有FEM/FEM 、FEM/BEM两种不同推导耦合方程的方法[6-7]。对于工程应用和复杂结构的分析，目前主要借助商用有限元软件计算完成。

目前舰船钢质附体结构大多为非耐压加筋夹层结构，内部设置纵横筋板，表层为薄钢板，整体为悬臂结构，本文所探讨的密加筋夹层结构也具有这种结构特性，是舰船附体结构的一种简化模型。研究附体结构水下振动的内域耦合问题时，可通过给密加筋夹层结构内部注水，来模拟附体结构内部充水的工作状况。附体结构内部的加筋板将流体分成多个小的流体域，流固交界面变成多个独立的区域。计算结构固有频率时若考虑流体与结构的耦合作用，针对耦合面的积分将变得极为复杂，从而导致计算量变得异常巨大。因而在仿真计算中有必要寻求替代方法。本文使用有限元分析软件ABAQUS计算结构低阶固有频率和振型，并提出一种等效的计算方法：将板格内的流体质量以非结构质量的形式附加到结构上，并对这种等效方法的适用性进行了探讨，最后将仿真计算结果与试验进行对比，表明所采用的方法是可行的。

1　流固耦合基本理论

1.1流体运动方程

对于无自由液面的内域耦合问题(见图1)，流体域的边界只存在于流固耦合交界面，在流固交界面上有

(1)

2φ

(2)

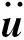
∭ΩN(3)

离散化后的流体运动方程式表示为：

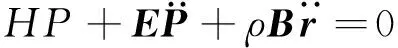
(4)

式中：H=∭ΩNNTdΩ，E=∭ΩNNTdΩ；。

图1　无自由液面的内域流固耦合系统Fig.1 Inner fluid of FSI system without free surface

1.2流固耦合方程

不考虑阻尼和外力作用时，结构的运动方程式

(5)

式中：fP为流固交界面上流体节点作用于结构的动压力矢量，集合全部流体元的贡献，方程变为

(6)

式中压力P和系数矩阵B的定义与流体运动方程相同，因而流体运动方程和结构运动方程是耦合的，二者可并归成：

(7)

(8)

2　充水圆柱模型计算

2.1方法合理性评价

由于复杂结构的流固耦合计算成本过高，本文提出了一种等效替代的附加质量方法，将内部水的质量以非结构质量的形式附加到结构上，并进行固有频率和振型计算。为讨论等效替代方法的有效性，本文建立了一个充水圆柱壳数值计算模型，基本参数如下：半径a=100 mm，高度h=500 mm，厚度d=3 mm，材料属性设置为：E=205 GPa、ρs=7.8×10-6kg/mm3、v=0.3圆柱用壳单元建模，一端刚固。内部水的密度ρf=1.03×10-6kg/mm3，体积压缩模量K=2.1 GPa，用ABAQUS特有的声学单元建模，模型如图2所示。文中计算了圆柱在真空中的频率，并分别用声固耦合法和附加质量方法计算了充水圆柱的前10阶固有频率，计算结果如图3。其中ABAQUS声固耦合方法采用声学单元来模拟流体，用以研究包括流固介质之间动态交互作用的许多现象，文献[9-10]就其计算精确度进行了讨论和验证，文中的所列的声固耦合法计算，其本质还是流固耦合计算。

图2　圆柱壳有限元模型Fig.2 Cylindrical shell finite element model

结果显示用附加质量方法计算值和声固耦合法相近，但前10阶固有频率中也存在一定差别。由模态分析理论[11] ，某阶振型在一个自由度方向的有效质量计算式为：

(9)

表1　主要振型和有效质量

2.2参与度概念提出

前文中介绍了流固耦合方程的推导，其中式(8)的推导是基于流体不可压缩前提的。但对于内域耦合问题流体问题而言，考虑不可压缩只适用于存在自用液面的情况[12]。文中充水圆柱壳计算模型不存在自由液面，因此在进一步探讨前需要对流体可压缩性进行讨论。流体不可压缩意味着体积模量K趋向于无穷大，在进行ABAQUS声固耦合计算时，需要设定声学单元的体积压缩模量为K，图4给出了圆柱壳固有频率随流体体积压缩模量的变化曲线(横坐标为对数刻度)，从图4可知随着流体的体积压缩模量的不断变大，固有频率趋于定值，K=2.1 GPa时的固有频率和K趋于无穷大时的值一致，由此认为虽然计算模型考虑了流体的可压缩性，但就水这种流体介质而言，其计算结果和不可压缩是一致的，因而适用于式(8)。

图4　固有频率随体积压缩模量的变化曲线Fig.4 Variation curve of eigenfrequencies with bulk modulus

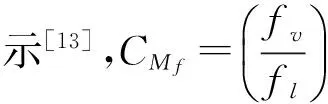
(10)

2.3方法适用性探讨

为探讨附加质量计算方法的适用范围，文中选取一系列的充水圆柱壳计算模型，半径为40～260 mm，高度为半径的5倍，厚度为3 mm，材料属性设置如前。文章计算了各模型的首阶振型流体参与度系数，结果见图5。

图5　流体参与系数随圆柱半径变化曲线Fig.5 Variation curve of fluid participation factors with radius

可以看出，随着圆柱壳半径和高度的增大，首阶振型的流体参与度系数呈增大趋势，当圆柱壳半径大于200 mm时η>1。附加质量方法和声固耦合法计算结果的比值如图6所示。起始点表示当结构圆柱趋于无限小时，内部流体小到可以忽略不计，此时附加质量方法和声固耦合法计算结果是一致的。随着流体参与度系数η的增大，附加质量方法与声固耦合法计算结果的比值fadd mass/ffluid呈现先降低后升高的趋势，当η>1时，faddmass/ffluid的比值逐渐接近于1，并随着η进一步增大而增大，最后比值大于1。以声固耦合法计算结果为标准，faddmass/ffluid值越接近1表示附加质量替代计算方法的计算精度越高，由此可以得出结论，流体参与度系数在η≈1的区段内，采用附加质量替代方法有较高的计算精度。

图6　附加质量方法和声固耦合法计算结果比值变化曲线Fig.6 Variation curve of faddmass/ffluid

进一步分析，由于所有圆柱壳的厚度均为3 mm，半径和高度较小的圆柱壳，其结构刚度和抵抗变形的能力相比半径和高度大的圆柱壳要强。对于半径和高度较小的圆柱壳，流体动压力变化所能引起结构的位移r极小，而圆柱壳内又不存在自由液面，因此流体对结构的影响表现为流体质量随结构运动。当η<1时，流体质量在系统运动自由度方向并未全部激发，亦即部分流体质量参与结构运动。此时应用附加质量方法将全部的流体质量附加到结构上，将引起计算结果偏低；当η≈1时，全部流体质量参与结构运动，此时附加质量计算方法结果接近声固耦合法；当η>1时，随着半径和高度的增大，流体动压力引起的结构位移r相对变大，此时流体对结构的作用不仅仅表现为附加质量的影响，还会产生流体与结构的耦合作用[15]。从计算结果看，此时附加质量方法的计算结果比声固耦合方法的计算结果偏高，且存在振型有效质量占比的明显变化(见表2)。

表2　固有频率和有效质量占比(a=260 mm)

3　加筋夹层钢结构模态计算和试验

3.1固有频率计算

加筋夹层钢结构总体尺寸为1 150 mm×500 mm×50 mm，所用钢板板厚均为3mm。纵横加筋将夹层结构分割成独立的小板格区域。整体采用实体单元建模，划分网格为8节点六面体单元，端部为试验工装。边界条件为工装刚固，有限元模型如图7所示。

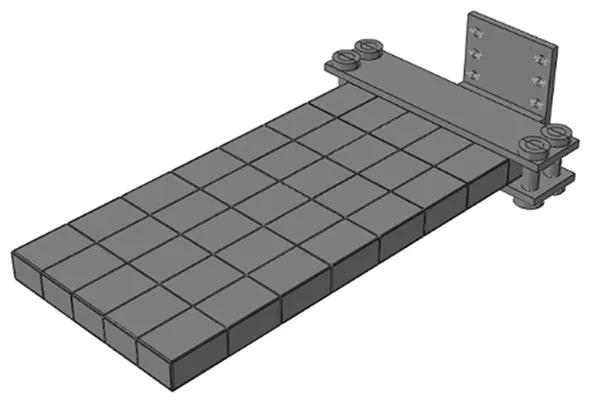
图7　加筋夹层结构有限元计算模型Fig.7 Finite element model of the reinforced sandwich structure

由于板格区域的相对独立，采用ABAQUS声固耦合计算方法将带来异常巨大的计算量，因而考虑采用附加质量法进行计算。进行计算之前，取一个单一的板格区域计算内域流体的参与度系数情况，结果表明计算单一板格的低阶振型时η在1附近，因此可以认为在计算结构整体固有频率时，内域流体主要以附加质量的形式影响结构。

3.2模态激振试验

通过单点激励多点输出的模态试验，测试了加筋夹层钢结构在无水/充水工况下的固有频率和模态振型，测试系统工作原理如图8所示。加筋夹层钢结构空重42.5 kg，充水后重76.95 kg，一端通过工装固定在桁架立柱上，整体为悬臂结构。激振源为JZT-50激振器，采用弹性吊装。信号源输出正弦扫频信号，扫频范围2～500 Hz。加速度传感器布置如图9。激振测试系统和测试试验如图10。

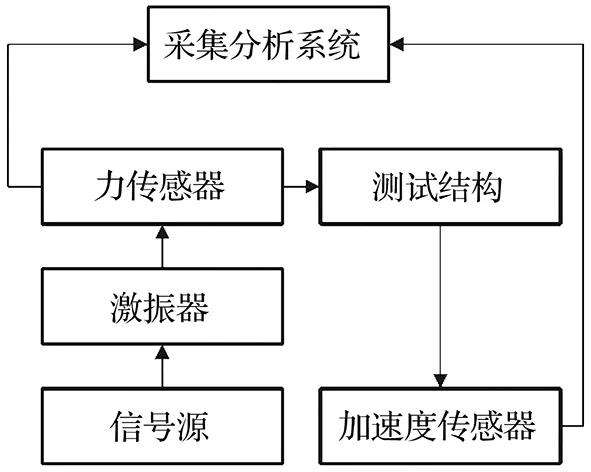
图8　测试系统工作原理示意图Fig.8 Schematic diagram of the test system

图9　加速度测点布置图Fig.9 Measuring-point of acceleration arrangement

图10　测试系统和激振试验Fig.10 Test and measuring system and the excited test

3.3仿真和试验结果对比

对比仿真和试验的无水/充水工况的前三阶固有频率和模态振型。固有频率结果如表3～4所示，无水工况的仿真/试验前三阶模态振型如图11所示，充水工况的低阶模态振型与无水类似，但频率比后者低。

表3　无水工况固有频率计算试验对比

表4　充水工况固有频率计算试验对比

图11　无水状态仿真和试验的前三阶振型Fig.11 The top three order modes of simulation/experiment without water

需要说明的是，这里的一阶、二阶、三阶是依据试验测试结果来定的，分析试验数据时读取对各测点响应曲线峰值点对应的频率，选出各测点均对应的第一、二、三阶共振频率。由于试验只考虑了垂直于板面方向的加速度响应，故在仿真计算中也只选取的与试验相应的振型，其余模态振型不作为对比对象。

无水工况下，试验和仿真首阶固有频率相差17.72%，分析认为属于工装边界设定的影响，仿真计算中通过限定工装自由度将边界条件设为刚固，而在实际试验中很难做到绝对刚性固定，从而导致仿真计算结果较试验结果偏高；充水工况下，试验和仿真的首阶固有频率相差18.53%，考虑到工装边界条件的影响，分析认为仿真计算是合理可信的，二阶和三阶固有频率仿真和计算值相差小于10%，符合工程精度的要求。综上，附加质量的替代方法在计算加筋夹层钢结构内域耦合问题时具有一定精度，可以用来计算结构的低阶特征频率和振型。

4　结　论

针对加筋夹层钢结构的内域流固耦合计算问题，提出了附加质量的替代方法，并通过充水圆柱壳计算模型探讨了附加质量方法的适用性。a提出了流体参与度的概念，当流体参与度系数η≈1时，附加质量方法具有较好的计算精度；b附加质量方法在计算加筋夹层钢结构充水模态时误差满足工程精度要求，可以用来计算结构的低阶固有频率和振型。

[1] 刘焕忠，李青 ，庄茁，等. 发展附加质量模型应用于储液罐的动力分析[J]. 工程力学，2005,22(6)：161-171.

LIU Huan-zhong， LI Qing，ZHUANG Zhuo. Development of added mass model and application todynamic analysis of cylindrical tanks[J].Engineering Mechanics，2005,22(6)：161-171.

[2] 程玉鑫，周力，洪明，等.舱内液体附加质量对振动影响的模型试验研究[J].中国舰船研究，2008，22(3)：64-67.

CHENG Yu-xin,ZHOU Li, HONG Ming, et al. Ship model experimental study on the effect of added masses caused by inner liquid on hull’s vibration[J].Chinese Journal of Ship Research，2008，22(3)：64-67.

[3] 谢志勇，周其斗，纪刚. 双层柱壳的流固耦合模态计算与试验研究[J] .海军工程大学学报，2009，21(2)：98-101.

XIE Zhi-yong, ZHOU Qi-dou, JI Gang. Computation and measurement of double shell vibration mode with fluid load[J].Journal of Naval University of Engineering，2009，21(2)：98-101.

[4] Kutin J, Bajsi I. Fluid-dynamic loading of pipes conveying fluid with a laminar mean-flow velocity profile[J].Journal of Fluids and Structures,2014, 11(2):171-183.

[5] 邢景棠，周盛，崔尔杰. 流固耦合力学概述[J].力学进展，1997，25(1)：19-38.

XING Jing-tan,ZHOU Sheng,CUI Er-jie.A survey on the fluid-solid interaction mechanics[J] Advances in Mechanics，1997，25(1)：19-38.

[6] 王峥，洪明，刘城. 基于 FEM/BEM 的浸水结构振动及声辐射特性国内研究综述[J].船舶力学，2014,18(11)：1394-1411.

WANG Zheng, HONG Ming, LIU Cheng. Domestic review of the submerged structure vibration and acoustic radiation characteristics based on FEM/BEM[J] Journal of Ship Mechanics. 2014,18(11)：1394-1411.

[7] Bordón J D R, Aznárez J J, Maeso O. A 2D BEM-FEM approach for time harmonic fluid-structure interaction analysis of thin elastic bodies[J]. Engineering Analysis with Boundary Elements,2014,43(6):19-29.

[8] 陆鑫森.高等结构动力学[M].上海：上海交通大学出版社，1992.

[9] Dassault systems similar Corp． Abaqus Theory Manual[M]． Pawtucker USA: ABAQUS， INC， 2008．

[10] 缪旭弘，钱德进，姚熊亮，等. 基于ABAQUS声固耦合法的水下结构声辐射研究[J].船舶力学，2009，13(2)：319-323.

MIAO Xu-hong，QIAN De-jin，YAO Xiong-liang,et al.Sound radiation of underwater structure based on coupled. [J].Journal of Ship Mechanics,2009，13(2)：319-323.

[11] Clough R W, Penzein J L. Dynamics of Structures[M]. McGraw-Hill,1986.

[12] Sisgrist J F, Broc D, Laine C. Dynamic analysis of a nuclear reactor with fluid-structure interaction Part I:Seismic loading,fluid added mass and added stiffness effects[J].Nuclear Engineering and Design,2006,236(3):2431-2443.

[13] De La Torre O, Escsler X, Egusquiza E. numerical and experimentenl study of a nearby solid boundary and partial submergence effects on hydrofoil added mass[J]Computers & Fliuds,2013,91(11):1-9.

[14] Valentin D, Presas A, Egusquiza E. Experimental study on the added mass and damping of a disk submerged in a partially fluid-filled tank with small radial confinement[J].Journal of Fluids and Structures,2014,50(7):1-17.

[15] Sisgrist J F, Broc D, Laine C. Dynamic analysis of a nuclear reactor with fluid-structure interaction Part Ⅱ:Shock loading,influence of fluid compressibility[J].Nuclear Engineering and Design,2007,237(7):289-299.

Natural characteristics simulation and tests for water-filled multi-stiffened sandwich structures

WU Dajiang, MEI Zhiyuan, WANG Yongli

(Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China)

For water-filled multi-stiffened sandwich structures, modal analysis spent too much time considering coupling of inner water and structure. To overcome this difficulty, a kind of alternative additional mass method based on ABAQUS was put forward. Simultaneously, the applicability of the additional mass method was discussed through analyzing water-filled cylindrical shell models with different radii and heights. In order to evaluate directly the fluid effects on natural frequencies of structures, the concept of fluid participation factor was introduced. It was pointed out that the calculation results of the additional mass method is accurate when the fluid participation factor is close to 1. Finally, the additional mass method was adopted to calculate modes of water-filled multi-stiffened sandwich structures, the results were compared with the test ones. The results showed that the additional mass method is feasible.

additional mass method; fluid-structure coupling; reinforced sandwich structure; finite element method

国家自然科学基金资助项目(51479205)

2015-05-14修改稿收到日期：2015-08-11

武大江 男，硕士，1990年10月生

梅志远 男，博士，教授，1973年9月生

TB21

A

10.13465/j.cnki.jvs.2016.15.022