曲率模态在检测环境温度下简支梁损伤中的应用

刘 昊，常 军

（苏州科技大学 土木工程学院，江苏 苏州215011）

近年来，环境因素下的桥梁损伤检测越来越受到重视。在实际应用过程中，结构受到环境因素（如温度）的影响，结构动力学参数会随环境因素的改变而发生变化[1]。在温度变化下，正常梁频率变化曲线较陡，损伤梁频率变化曲线比较平缓，而且损伤越重曲线越平缓，在相同温度变化范围内，损伤梁频率变化受温度变化影响较小，而正常粱频率变化受温度变化影响较大[2]，即损伤对结构频率的影响会湮没在温度的影响中[3]。为了剔除或减少环境温度对结构的影响，得到结构本身损伤或无损的真实状态，需要考虑寻求某个不受温度影响或影响很小的结构特征参数。

1982年，Allemany和Brown[4]利用结构损伤前后的某阶振型定义了一个可用于损伤识别的指标，随后Lieven和Ewins[5]对这一指标提出了改进。模态振型是关于位置的函数，通过对比损伤前后的振型差可以确定结构的损伤位置，但存在对模态振型节点损伤不敏感和不能有效反应损伤程度的问题[6]。由此Pandy和Biswas等[7]则提出可利用结构损伤前后的振型曲率对结构的损伤进行诊断,并成功地对一悬臂梁和一简支梁的损伤进行了检测。本文以一简支梁为研究对象，考虑环境温度变化情况，通过有限元模拟分析得到梁在无损及各损伤工况下的多阶模态振型，后通过数值分析得出振型曲率，研究梁在环境温度因素下的结构损伤识别和定位。

1 有限元建模

图1为两端简支的矩形截面梁，截面尺寸200 mm×500 mm，梁长4 m，材料的弹性模量为32.6 GPa，密度为2 650 kg/m3，泊松比为0.3。由此尺寸建立简支梁的有限元模型，沿着长度的方向划分8个单元，单元长度为0.5 m。由结构动力学，弹性模量与刚度成正比，故采用降低弹性模量的方式来模拟单元的损伤[8]。

图1 简支梁模型

2 温度对振型影响分析

通过有限元模拟温度变化对结构影响，需要设置材料的线膨胀系数。该简支梁为混凝土梁，根据《混凝土结构设计规范》（GB 50010-2010）：混凝土结构设计时，当温度在0～100℃范围内时，线膨胀系数为0.000 01/℃。取线膨胀系数为10-5/℃。分析简支梁结构无损情况下分别在20℃和40℃时的振型，并绘制振型图，如图2所示。由有限元软件分析得出各点相对于某坐标的相对位移来确定梁的振幅，将各位移分量除以于其最大幅值，即采取归一化处理，把向量表示为无量纲的形式，即得简支梁的各阶振型。图2（a）-（d）分别为简支梁的前四阶振型，如图2可见，前四阶振型在不同温度下的两条振型曲线完全重合，所以温度变化对简支梁无量纲振型不产生影响。

表1 简支梁损伤工况

图2 不同温度下无损结构振型图

3 损伤对振型影响分析

选取无损结构、工况一、工况二对比分析损伤位置对结构振型的影响，如图3、图4所示，三条曲线在一阶和二阶振型下均很接近，需要局部放大才能看清，各工况下及无损情况的振型曲线并不重合，损伤位置对结构振型有影响，但在损伤部位无法通过振型曲线的变化找出规律性现象，无法通过图示振型判断损伤位置；选取无损结构、工况二、工况三对比分析损伤程度对结构振型的影响，如图5和图6所示，一阶振型下损伤程度越高振型曲线越平缓（曲线靠上），而二阶振型情况相反，损伤程度越高振型曲线越陡（曲线靠下），没有形成规律性现象，且仍需对图形进行局部放大，判断损伤程度效果较差。故不采用结构振型来判断结构损伤的位置及程度。

图3 损伤位置对一阶振型的影响

图4 损伤位置对二阶振型的影响

图5 损伤程度对一阶振型的影响

图6 损伤程度对二阶振型的影响

4 损伤对振型曲率影响分析

对于梁类结构,某一截面的曲率v"可以表示为[9]

其中，M 为截面弯矩；EI 为截面的抗弯刚度。 式（1）表明，梁的截面曲率与截面刚度密切相关[10]，截面刚度的下降可以明显地反映在其曲率的改变上来[11]。 从本质上看,曲率就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度。其反映的是转角的变化率,而转角反映的是位移的变化率。 因此,如果结构的某个部位出现损伤,则结构在这个局部的曲率应明显大于其他部位的曲率[12]。 这正是利用振型曲率对结构进行损伤检测的出发点。 由此考虑通过结构振型曲率来进行分析，由曲率公式

计算无损及各工况下的结构振型曲率，绘制成图，结构损伤的位置及程度对各工况下前三阶振型曲率的影响如图7-图12 所示。

由图7、9、11 看出，简支梁振型曲率在损伤处发生突变，其他部位振型曲率则基本与无损情况的振型曲率曲线基本重合，表明简支梁的振型曲率可以用作损伤定位，但是随着阶次的增高，如图11 的三阶振型曲率， 在损伤部位曲率线条两端会出现反向毛刺状凸起。 损伤程度对简支梁振型曲率的影响如图8、10、12 所示，损伤程度越大，振型曲率在损伤处的突变幅度越大，同样随着阶次增高，损伤部位两端会出现毛刺状突起，损伤程度越高，越明显。 笔者认为出现毛刺原因可能由于，在有限元模拟中通过改变弹性模量来模拟损伤，即损伤部位的刚度产生变化，所以在损伤部位两端出现刚度突变而导致。

以上分析均只考虑了结构出现单处损伤的情况，但在实际结构生命周期内，经常会同时出现多处损伤。因此选取工况4 与无损结构进行对比，分别计算简支梁结构振型曲率，如图13、14 所示，分析多处损伤对振型曲率的影响。

图7 损伤位置对一阶振型曲率的影响

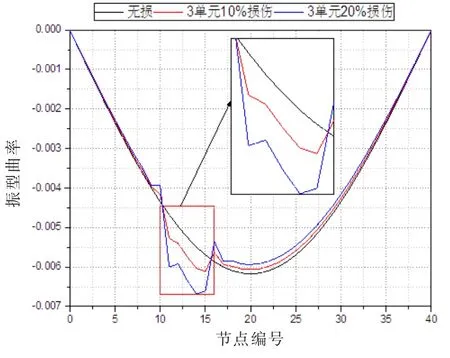
图8 损伤程度对一阶振型曲率的影响

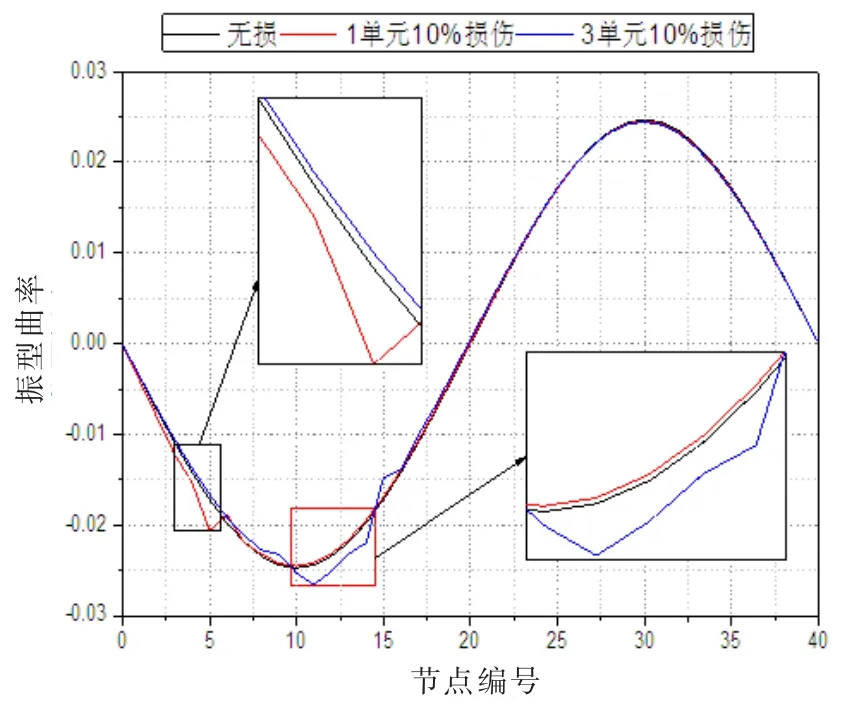
图9 损伤位置对二阶振型曲率的影响

图10 损伤程度对二阶振型曲率的影响

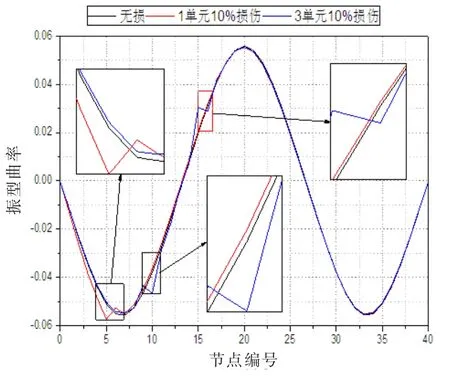
图11 损伤位置对三阶振型曲率的影响

图12 损伤程度对三阶振型曲率的影响

图13、14中，简支梁的振型曲率在各损伤部位处均发生突变，其余部位振型曲率曲线与无损状态曲线基本重合。结果表明，对于多处损伤的简支梁结构，振型曲率也能很好的作出识别定位。

图13 多处损伤对一阶振型曲率的影响

图14 多处损伤对二阶振型曲率的影响

5 结论

通过建立含损伤的简支梁有限元模型，使用有限元进行分析，研究了在环境温度下结构损伤对简支梁振型及振型曲率的影响，得出以下结论：

（1）环境温度的改变对结构振型及振型曲率没有任何影响。在进行结构损伤识别、定位时可以忽略温度的影响；

（2）损伤结构与无损状态下振型的差别随结构损伤程度的增大而增大，但损伤对简支梁振型的影响较小。通过简支梁振型的变化无法对损伤进行定位；

（3）简支梁的振型曲率在损伤部位会形成突变，且随着损伤程度的增大，损伤处的突变幅度也增大。随着阶次的增高，损伤部位两端会出现毛刺状突起，损伤程度越高越明显；

（4）对于多处损伤的简支梁，其振型曲率依然在损伤处发生突变。

简支梁的振型曲率可以对结构的损伤进行有效的识别、定位，对多损伤结构仍然适用。低阶振型的曲率识别效果要好于高阶振型曲率。本文的有限元建模和识别方法可以用于分析其它边界条件的梁或连续梁。