基于波动法的静水压力下环肋圆柱壳耦合振动特性研究

梁 斌，李 戎，刘小宛，NODA Nao－Aki，徐红玉

(1.河南科技大学 土木工程学院，河南 洛阳 471023;2.九州工业大学 机械系，日本 北九州 804－8550)

由于肋骨加强的圆柱壳体结构能够在减小自身重量的前提下达到增强结构刚度和强度的作用，加肋圆柱壳已被广泛应用至潜艇耐压船体结构、航空航天等领域，研究环肋圆柱壳在静水压力下的振动特性对于研究水下圆柱壳体结构的力学行为有着非常重要的意义。Junger［1－2］最早对浸没在声场中的各向同性圆柱壳进行研究。Zhang等［3－4］利用波动法研究了考虑流体影响的圆柱壳的振动特性。Loy等［5］利用Rayleigh－Ritz法研究了仅含有一条环肋时圆柱壳的振动特性。Liu等［6］考虑了静水压力对水下环肋圆柱壳输入功率的影响。Gan等［7］以环肋圆柱壳为研究对象讨论了波动法在对此类问题进行分析时的计算精度问题。Tatianna等［8］采用 Flügge 壳体理论研究了侧向压力下圆柱壳体的稳定性。Zhu等［9］基于波动法讨论了通过壳体的固有频率和静水压力来得到不加肋水下圆柱壳临界压力的方法的可行性。

本文在Flügge理论的基础上，考虑流体的影响，采用波动法得到耦合系统的振动方程。再通过变换轴向波数，利用牛顿迭代法得到连续变化的静水压力下、不同边界条件时水下圆柱壳的固有频率。通过分别退化计算不考虑液体影响的环肋圆柱壳和水下不加肋圆柱壳的固有频率，验证了本文方法的有效性和正确性。作为算例，计算并分析了肋条尺寸和数目、静水压力、边界条件等因素对壳体固有频率的影响。

1 力学模型

假定环肋圆柱壳(外加肋)如图1所示，半径为R，长度为L，壁厚为h，肋条截面长度为hr，宽度为 br，肋条间距为d2。将正交坐标系(x，θ，z)建立在壳体中面上，其中x，θ和z分别为壳体的轴向、环向和径向坐标。

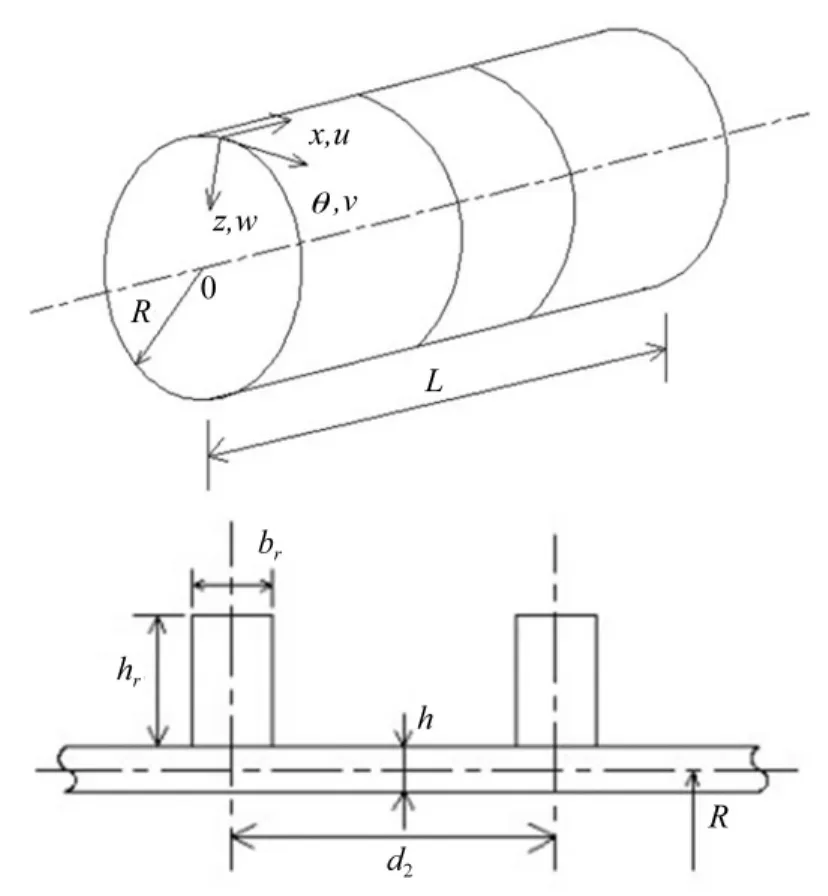
图1 环肋圆柱壳模型Fig.1 Geometry of a ring-stiffened cylindrical shell

2 理论推导

由Flügge［10］理论可以得到考虑静水压力时圆柱壳的运动方程

圆柱壳的振动位移函数可以表示为

式中，Um，Vm，Wm分别表示 x，θ，z方向的波幅，ω 为固有角频率。

考虑液体影响的圆柱壳满足声波方程，在柱坐标系(x，θ，r)中，流体的运动方程为

式中，t为时间，c为流体的声速，ψ为声压，r坐标沿壳体径向选取。而在流体中，满足声波方程(3)的声压场在柱坐标系中的形式，可以表示为

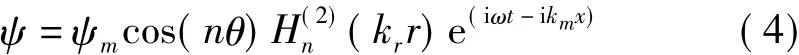
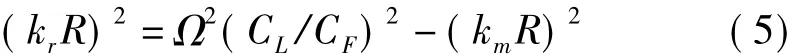
式(5)中，Ω，CL和CF分别为无量纲频率参数，圆柱壳体的声速及流体的声速。由于在壳体外壁与流体的接触界面上，流体径向位移与壳体径向位移必须相等。该耦合条件表达式为

针对不同情况，代入具体的边界条件至km［11］，求解式(8)，可以得到

式中，P1(ω)和P2(ω)分别为关于未知数ω的多项式。在一定外压下，采用牛顿迭代法即可得到给定静水压力时环肋圆柱壳的固有频率值。当FL=0，Q=0时，即可还原为不考虑流体影响情况下环肋圆柱壳的固有频率的计算。

3 算例与讨论

表1计算了静水压力下，不考虑肋条影响时三种边界条件下圆柱壳的固有频率。通过与Zhu［9］的结果进行对比，验证了本文在计算静水压力下壳体固有频率时的有效性和正确性。壳体的几何参数为:E=2.1×1011N/m2，μ =0.3，ρ=7 850 kg/m3，L/R=20，h/R=0.01，R=1 m，m=1，n=2。

表1 不同边界条件下水下圆柱壳固有频率的对比分析Tab.1 Comparison offundamental natural frequencies under different hydrostatic pressures in various boundary conditions

表2计算了两端简支边界条件下，不考虑液体影响时环肋圆柱壳的固有频率。通过与参考文献［7，12］的结果进行对比，验证了本文在计算环肋圆柱壳的固有频率时的有效性和正确性。

由于当静水压力超过临界压力时，结构会失稳，再进行固有频率的计算已无意义，所以对圆柱壳容器进行结构分析时，需要考虑其临界压力大小。而对于静水压力下的环肋圆柱壳，当壳体的固有频率为0时，则可认为此时所对应的静水压力即为环肋圆柱壳临界荷载的弹性理论解。因此，本文在进行水下环肋圆柱壳的振动特性分析时，静水压力数值均控制在其壳体分别对应的临界压力以下。作为算例，本文分别计算了连续变化的静水压力下，变换h/R、轴向半波数、肋条尺寸和数目、边界条件等多种影响因素时圆柱壳的固有频率变化曲线，见图2至图10。壳体的几何参数为:E=2.077 88 × 1011N/m2，μ =0.317 756，ρ=8 166 kg/m3，L/R=20，R=1 m，m=1，hr=0.005 m，br=0.003 m，肋条数 Nr=20。

表2 环肋圆柱壳固有频率的对比分析Tab.2 Comparison of natural frequencies of stiffened cylindrical shell

为了更好的表现肋条对于圆柱壳的固有频率的影响，下面首先以两端简支边界条件下的环肋圆柱壳作为研究对象，分析不考虑静水压力时肋条对壳体固有频率的影响，h/R=0.002。图2分别以不加肋和环肋圆柱壳作为研究对象，给出了不同轴向半波数时，两端简支边界条件下圆柱壳的固有频率的变化规律曲线。从图中可以看出，加肋圆柱壳的固有频率明显大于不加肋圆柱壳的固有频率，且随着周向波数的逐渐增大，肋条对固有频率的影响逐渐显现;与不加肋圆柱壳相比，肋条对壳体的固有频率的影响主要表现在周向波数较大的情况下;轴向半波数对固有频率的影响主要表现在周向波数较小的情况下。

图3给出了不同肋条数目(当壳体长度一定时，增减肋条数目等同于改变肋条间距)时，壳体固有频率的变化曲线。可以看出，随着肋条数目的不断增多(肋条间距的逐渐减小)，壳体的固有频率逐渐增大，肋条数目对固有频率的影响主要表现在周向波数较大的情况下;随着周向波数的逐渐增大，固有频率先减小后增大。

图4以肋条截面长度和宽度比作为出发点，研究了肋条尺寸对壳体固有频率的影响，br=0.003 m。由图可知，壳体的固有频率随着肋条截面长度和宽度比的增大而增大，且其比例值越大，频率增长幅度约明显;长度和宽度比对固有频率的影响主要表现在周向波数较大的情况下;与肋条数目(肋条间距)相比，肋条的截面长度和宽度比对固有频率的影响更为显著。

图5给出了不同h/R时环肋圆柱壳的固有频率曲线。如图所示，随着周向波数的逐渐增大，壳体的固有频率先减小后增大;固有频率随着h/R的增大而增大，且h/R对固有频率的影响主要表现在周向波数较大的情况下。

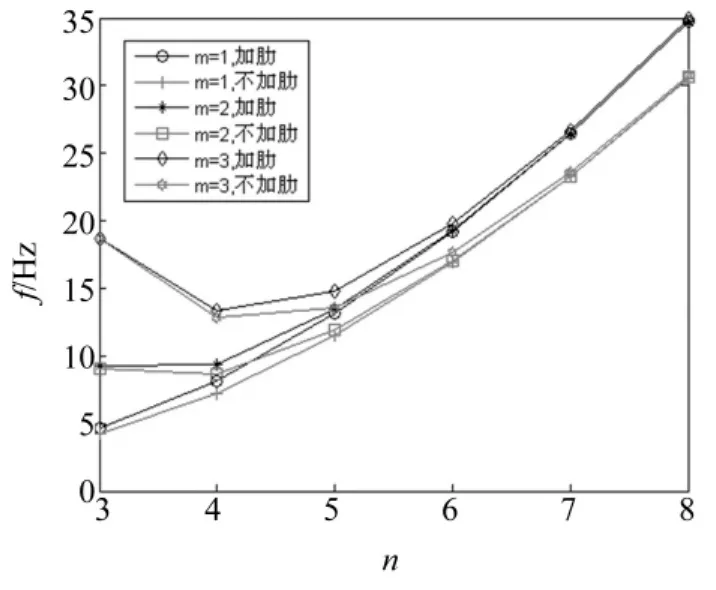
图2 不同轴向半波数m时圆柱壳的固有频率的变化规律曲线Fig.2 Variation of natural frequencies of cylindrical shells for some different axial half wave numbers

图3 不同肋条数目时圆柱壳的固有频率的变化规律曲线Fig.3 Variation of natural frequencies ofring-stiffened cylindrical shells for the number of Nr

图4 不同hr/br时圆柱壳的固有频率的变化规律曲线Fig.4 Variation of natural frequencies for a ring-stiffened cylindrical shells with different hr/br ratios

图5 不同h/R时环肋圆柱壳的固有频率变化曲线Fig.5 Variation of natural frequency for a submerged ring-stiffened cylindrical shell with different h/R ratios

图6 不同轴向半波数m时圆柱壳的耦合频率和非耦合频率的变化规律曲线Fig.6 Variation of coupled and uncoupled frequencies of cylindrical shells for some different axial half wave numbers

图7 两端简支边界条件下水下圆柱壳的固有频率变化曲线Fig.7 Variation for a simply support submerged cylindrical shell

图6 －10给出了考虑液体影响时环肋圆柱壳的固有频率变化规律曲线，为了更好表现流体因素对壳体固有频率的影响。图6给出了仅考虑流体影响，静水压力Q=0时的固有频率曲线。可以看出声压对壳体的固有频率有显著的影响;随着周向波数的逐渐增大，耦合频率逐渐由非耦合频率的约1/5增大至非耦合频率的1/3;轴向半波数对固有频率的影响主要表现在周向波数较小的情况下。

选用h/R=0.01。图7给出了静水压力下，两端简支环肋圆柱壳的固有频率曲线。可以看出，随着静水压力的逐渐增大，壳体的固有频率逐渐减小;固有频率随着周向波数的增大而增大;当n=2，Q=80 kPa时，固有频率接近0，此时的静水压力即为壳体的临界压力。

基于上图结论，接下来将n=2时壳体固有频率作为研究对象。图8给出了静水压力下，不同肋条数目时壳体的固有频率。从图中可以看出，随着静水压力的不断增大，壳体的固有频率逐渐减小;不同肋条数目时壳体的固有频率非常接近，即肋条数目对壳体的固有频率的影响并不明显，当静水压力接近80 kPa，固有频率下降速度明显加快，不同固有频率之间的差别开始显现;当Nr=0时，壳体的固有频率下降速度变快。

图9给出了静水压力下，不同边界条件时环肋圆柱壳的固有频率变化曲线。可以看出，壳体的固有频率随着静水压力的逐渐增大而减小，接近临界压力时固有频率下降速度变快;五种边界条件中，两端固定边界条件下的固有频率最大，一端自由一端滑移边界条件下的固有频率最小;一端自由一端滑移和一端固定一端自由这两种边界条件下的固有频率非常接近;当静水压力为50 kPa时，一端自由一端滑移边界条件下的固有频率接近0，达到临界静水压力。

图10给出了静水压力下，不同h/R时壳体的固有频率。由图可知，壳体厚度对固有频率的影响非常显著;随着静水压力的增大，壳体的固有频率逐渐减小，当h/R=0.002时固有频率下降速度最快;壳体的固有频率随着h/R的增大而增大，且固有频率的下降速度随着h/R的增大而迅速变缓。

图8 静水压力下不同肋条数目时圆柱壳的固有频率的变化曲线Fig.8 Variation of natural frequencies of ring-stiffened cylindrical shells for the number of Nr under hydrostatic pressure

图9 不同边界条件下环肋圆柱壳的固有频率曲线Fig.9 Variation of natural frequency for a submerged ring-stiffened cylindrical shell with different boundary conditions

图10 不同h/R时水下环肋圆柱壳的固有频率变化曲线Fig.10 Variation of natural frequency for a submerged ring-stiffened cylindrical shell with different h/R ratios under hydrostatic pressure

4 结论

本文基于Flügge理论并考虑流体影响，采用波动法研究了静水压力下环肋圆柱壳的耦合振动特性。

(1)环肋圆柱壳的固有频率明显大于不加肋圆柱壳的固有频率;肋条对固有频率的影响主要表现在周向波数较大的情况下;轴向半波数对固有频率的影响主要表现在周向波数较小的情况下。

(2)肋条数目对固有频率的影响主要表现在周向波数较大的情况下;壳体的固有频率随着肋条截面长度和宽度比的增大而增大，且其比例值越大，频率增长幅度约明显;长度和宽度比对固有频率的影响主要表现在周向波数较大的情况下;与肋条数目(肋条间距)相比，肋条的截面长度和宽度比对固有频率的影响更为显著。

(3)固有频率随着h/R的增大而增大，且h/R对固有频率的影响主要表现在周向波数较大的情况下;当考虑流体影响时，随着静水压力的增大，壳体的固有频率逐渐减小，当h/R=0.002时固有频率下降速度最快;壳体的固有频率随着h/R的增大而增大，且固有频率的下降速度随着h/R的增大而迅速变缓。

(4)随着静水压力的逐渐增大，壳体的固有频率逐渐减小;当静水压力接近临近压力时，固有频率下降速度明显加快。

(5)五种边界条件中，两端固定边界条件下的固有频率最大，一端自由一端滑移边界条件下的固有频率最小;一端自由一端滑移和一端固定一端自由这两种边界条件下的固有频率非常接近;当静水压力为50 kPa时，一端自由一端滑移边界条件下的固有频率接近0，达到临界静水压力。

［1］Junger M C.Radiation loading of cylindrical and spherical surfaces［J］.Acoust.Soc.Am.，1952，24(3):288 －289.

［2］Junger M C.Vibrations of elastic shells in a fluid medium and the associated radiation of sound ［J］.Appl.Mech.，1952，19(3):439 －445.

［3］Zhang X M，Liu G R，Lam K Y.Coupled vibration analysis of fluid-filled cylindrical shells using the wave propagation approach［J］.Applied Acoustics，2001，62(3):229 －243.

［4］Zhang X M.Frequency analysis of submerged cylindrical shells with the wave propagation approach［J］.International Journal of Mechanical Sciences，2002，44(7):1259－1273.

［5］Loy C T，Lam K Y.Vibration of cylindrical shells with ring support［J］.International Journal of Mechanical Sciences，1997，39(4):455 －471.

［6］ Liu Z Z，Li T Y，Zhu X，et al.Effect of hydrostatic pressure on input power flow in submerged ring-stiffened cylindrical shells［J］.Journal of Ship Mechanics.2011，15(3):301－312.

［7］ Gan L，Li X B，Zhang Z.Free vibration analysis of ringstiffened cylindrical shells using wave propagation approach［J］.Journal of Sound and Vibration，2009，326(3 －5):633－646.

［8］Vodenitcharova T， Ansourian P. Buckling of circular cylindrical shells subject to uniform lateral pressure［J］.Eng.Struct.，1996，18(8):604 －614.

［9］Zhu X，Ye W B，Li T Y，et al，The elastic critical pressure prediction of submerged cylindrical shell using wave propagation method［J］.Ocean Engineering，2013，58:22－26.

［10］ Flügge W.Stresses in shells［M］.Second Edition.Springer -Verlag，New York，1973.

［11］Zhang X M，Liu G R，Lam K Y.Coupled vibration analysis of fluid-filled cylindrical shells using the wave propagation approach［J］.Applied Acoustics，2001，62(3):229 －243.

［12］Jafari A A，Bagheri M.Free vibration of non-uniformly ring stiffened cylindrical shells using analytical，experimental and numerical methods ［J］.Thin-Walled Structures，2006，44(1):82－90.