电流谐波与轧制力谐波协同诱发主传动多态耦合振动研究
张义方,闫晓强,凌启辉
(1.北京科技大学 机械工程学院,北京 100083;2.马鞍山钢铁股份有限公司,安徽 马鞍山 243003)
连轧机振动问题是困扰轧钢生产的世界难题,随着对带钢表面质量要求越来越高,轧机振动问题成为带钢表面质量提升的一大瓶颈。许多专家和学者对轧机振动现象进行了大量的研究。近年来连轧机的振动研究已从过去单一因素研究提高到从耦合振动角度入手来开展研究[1-5]并取得了一些成果,研究发现在轧机系统中存在着各种变量控制参数耦合和多子系统相互耦合等多种耦合行为对轧机振动产生很大影响,因此研究轧机耦合行为对抑制振动具有重要价值。
1 问题提出
某热连轧F3轧机在轧制薄规格或高强度带钢时经常出现振动,利用自制的扭振遥测系统对主传动扭振进行了测试,扭振测试是将焊接式扭矩传感器用专用焊机焊在电机输出轴的表面上,信号由和轴一起旋转的内线圈与地面固定的静止外线圈之间的磁场耦合后经调理接入现场监测工控计算机数据采集系统(分辨率为0.5 Hz),力矩电流及轧制力信号由现场工艺采集系统提供(分辨率为0.1 Hz)。现场测试发现轧机主传动扭振波形及频谱中主要存在典型的强或弱两种振动特征现象。例如:一种典型较弱的扭振(如图1(a)所示)振动中心频率为41.5 Hz,同时含有18 Hz及49.5 Hz的频率,同一时刻主传动电机力矩电流及轧制力主频为49.6 Hz如图1(b);另外一种典型较强烈拍振中心频率也为41.5 Hz如图2(a),同一时刻电机力矩电流及轧制力主频都为41.9 Hz如图2(b)。初步认为:主传动扭振现象与主传动两端的激励频率紧密相关,为了说明这一现象,试图用仿真分析来解释。

图1 弱耦合时信号特征Fig.1 Signal characteristic for weak coupling

图2 强耦合时信号特征Fig.2 Signal characteristic for Strong coupling
2 主传动机械固有频率计算
为了求解主传动机械系统固有频率,依据现场提供的CAD图纸及有关参数,建立有限元模型如图3。经过仿真分析获得主传动机械系统的固有频率如表1。从表中可以看出:二阶固有频率与轧机强烈振动频率接近。

图3 F3轧机机械系统有限元模型Fig.3 Finite element model of mechanical system for F3 rolling mill

表1 F3轧机主传动系统扭振固有频率Tab.1 Natural frequency of torsional vibration for F3 rolling mill main drive system

图4 单相交-交变频器模型Fig.4 Single phase cycloconverter model
3 电流谐波与主传动机械系统耦合机制
针对该热连轧F3轧机的交-交变频供电系统,利用Matlab/Simulink中SimPowerSystems模块建立三相交流输入单相输出的交-交变频仿真模型如图4所示,模型中两组三相桥整流正组和逆组反并联连接,两个触发模块触发脉冲1和触发脉冲2的同步信号来自同步变压器。模型中两组三相桥采用逻辑无环流控制方式,逻辑控制器的输出信号分别连接触发器的block端,逻辑控制器根据给定信号和实际反馈电流信号极性确定两组整流器的工作状态。给定信号经绝对值变换和移相控制后连接触发器的alpha-deg端,改变正弦交流给定信号的频率和幅值,交-交变频器的输出电流频率和幅值作相应的变化。这里根据现场轧制速度选取变频器输出频率为7 Hz进行仿真,输出电流波形如图5所示。可见在输出频谱中除基频以外还产生谐波分量。为了分析含这些谐波分量的输出电流通过同步电机的磁场耦合会产生怎样的电机输出力矩。建立了三相交-交变频器和电动机联合模型如图6,电机采用电励磁凸极同步电动机,三组交-交变频分别给同步电机的三相供电,根据现场提供的参数仿真输出的电机定子电流和电磁力矩波形如图7和图8。
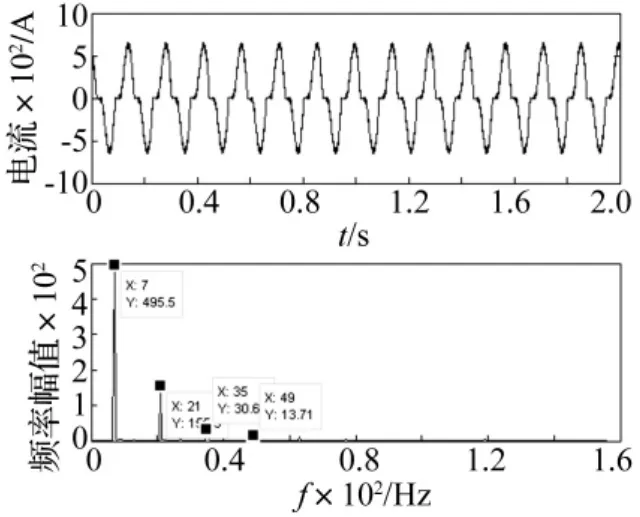
图5 变频器输出电流波形及频谱Fig.5 Waveform and spectrum of output current for cycloconverter

图6 三相变频器与电动机联合模型Fig.6 Model of three phase cycloconverter and motor
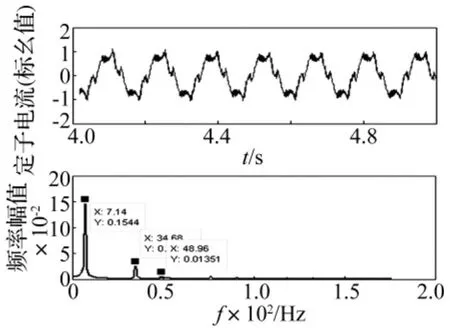
图7 定子电流波形和频谱图Fig.7 Waveform and spectrum of stator current

图8 仿真输出电机电磁力矩波形及频谱Fig.8 Waveform and spectrum of electromagnetic torque for simulation
从仿真波形上看:电动机在交交变频器控制运行时的定子电流除基频7 Hz外还有35 Hz(5次)和49 Hz(7次)谐波分量,电磁力矩信号中含有42 Hz振荡频率。初步确定变频谐波是产生电动机输出轴振荡的主要原因。实际上当谐波电流流过定子线圈绕组时,在绕组内感应出交变的磁势,三相绕组流过三相交流产生的磁势就会在电动机磁场空间产生相同频率的谐波磁势,5次负序谐波电流在空间产生反向的旋转磁势,相对于同步电动机基波磁场的旋转频率为-6ω=-5ω-ω,ω为同步电机磁场基波旋转频率即同步电机的工作转频。7次正序谐波电流在空间产生与基波磁场同向磁势,其旋转频率相对于基波磁场为6ω=7ω-ω,由此可见5次、7次谐波电流在同步电动机中相对于基波磁场的旋转频率相同,都为6次,当其和转子基波磁场作用,就会产生6倍基频(42 Hz)的电磁转矩,只是两者方向相反。这一谐波转矩叠加在同步电动机基波磁场产生的稳态转矩之上就造成了电动机输出转矩振荡,图2中频率42 Hz恰好为变频器输出基频7 Hz的6倍,因此它是由变频谐波电流和电动机基波磁场作用产生的谐波力矩频率。
可见同步电机输出轴力矩频率42 Hz为基频的6倍[6-7]。可以推测如果这一谐波频率和轧机主传动机械系统二阶固有频率耦合会诱发强烈振动[8-9]。也就是说谐波力矩越靠近主传动机械系统固有频率,耦合振动越强;远离固有频率,振动就会减弱。
4 轧制力谐波与主传动机械系统耦合机制
轧机液压压下系统是一个控制模型复杂、轧制力高、扰动参数众多、控制精度高和响应速度快的系统,它的主要功能是在一定轧制力下来控制带钢纵向的厚差。由于压下电液伺服阀本身的非线性特征,使得系统响应含有谐波分量[10-11]。根据压下液压缸及伺服阀等相关参数建立液压压下系统模型如图9,图中AGC伺服阀采用喷嘴挡板式二级控制电液伺服阀,通过它驱动轧机压下液压缸,压下缸活塞杆和轧机牌坊横梁固定在一起,液压缸外壳直接作用在轧机辊系轴承座上,图中轧机辊系以等效质量、刚度及阻尼代替。改变伺服阀的信号给定,在液压力的作用下,AGC缸外壳输出相同频率的作用力来改变轧机辊缝大小,达到调节带钢厚度的目的。假设F3轧机液压压下调节频率为6 Hz,仿真获得液压缸作用力(轧制力)波形及频谱如图10,从图中可以看出除6 Hz以外,还含有因系统非线性产生的谐波分量。由轧制理论可知,轧制力的变化会引起主传动系统扭矩的同频变化。在轧制过程中,由于液压压下的非线性变化产生的谐波分量通过轧制界面耦合到主传动扭矩中,当传动系统的扭矩中含有和主传动机械固有频率相近的谐波分量,就会诱发轧机传动系统的耦合振动,远离系统固有频率特性,振动就会减弱。

图9 AGC伺服阀驱动液压缸仿真模型Fig.9 Model for AGC servo-valve driving hydraulic cylinder

图10 液压缸输出力波形及频谱Fig.10 Waveform and spectrum of output force for hydraulic cylinder

图11 传动系统谐波激励仿真模型Fig.11 Simulation model of harmonic excitation on main drive system
5 电流谐波和轧制力谐波协同诱发多态耦合振动
为了同时研究电流谐波和轧制力谐波对主传动扭振的影响,通过Matlab/Simulink中的Simscape相关模块构建轧机主传动模型(图11)。在轧制过程中,随着轧制速度的变化,主传动电机电流谐波频率和轧制力谐波也会发生相应变化,这里分别以49 Hz和42 Hz两种特定谐波激励来进行研究。通常情况下,轧机轧制力增加,意味着轧制力矩增加,相应的轧机传动电机的电流也会增加,由上述的耦合机制可知:电流和轧制力谐波最终通过工作辊耦合在一起。
5.1 谐波远离固有频率时的现象
为了模拟现场测试结果,设两个谐波信号频率都为49 Hz,将主传动电机电流谐波力矩和轧制力产生的谐波力矩按照测试的实际值作为两个激励源施加在主传动系统上,仿真结果如图12所示。

图12 主传动轴扭振仿真输出波形及频谱Fig.12 Waveform and spectrum of torsional vibration on main drive shaft for simulation
5.2 谐波接近固有频率振动现象
参考现场测试参数值,设定现场两个谐波源激励频率为42 Hz,同样将主传动电机电流谐波力矩和轧制力产生的谐波力矩作为两个激励源施加在主传动系统上,仿真得到主传动轴扭振响应如图13所示。

图13 主传动轴扭振仿真输出波形及频谱Fig.13 Waveform and spectrum of torsional vibration on main drive shaft for simulation
从以上分析可见,当传动系统两个谐波激励频率远离主传动系统固有频率时,主传动系统振动较弱,出现了含有一阶和二阶及激励频率共存的多态耦合振动现象。而当谐波激励频率和机械系统二阶固有频率相近,主传动系统将发生强烈拍振,仿真得到的结论与现场实际测试结果相符。
6 结论
轧机主传动系统同时承受电流谐波产生的电磁力矩谐波和液压压下谐波产生的轧制力谐波协同激励下,主传动系统呈现多态耦合振动特征。主传动系统的多态耦合振动特征主要取决于谐波源的激励频率。在实际生产中,随着轧制速度的变化,两种谐波源的频率也跟随发生变化,在不同工况下会呈现强耦合和弱耦合状态。因此,抑制轧机振动可以从抑制谐波角度来开展工作,将强耦合状态降低到弱耦合状态,可以大大降低振动能量和振动现象。
[1]钟倔,唐华平.高速轧机若干振动问题-复杂机电系统耦合动力学研究[J].振动、测试与诊断,2002,22(1):1 -8.ZHONG Jue,TANG Hua-ping.Vibration problems of high speed rolling mill study of dynamics of complex electromechanically coupled system[J].Journal of Vibration,Measurement& Diagnosis,2002,22(1):1-8.
[2]张瑞成,童朝南.基于交流传动的轧机机电耦合系统振动特性分析[J].机械强度,2006,28(3):336-340.ZHANG Rui-cheng,TONG Chao-nan.Analysis vibration characteristic of electromechanical coupling system of rolling mill based on ac drive[J].Journal of Mechanical Strength,2006,28(3):336 -340.
[3]马维金,熊晓燕,李凤兰,等.热连轧机位移传感器结构的试验模态分析[J].机械工程学报,2009,45(7):259-264.MA Wei-jin,XIONG Xiao-yan,LI Feng-lan,et al.Modal parameter testing of roller gap sensor structure on hot rolling mill[J].Journal of Mechanical Engineering,2009,45(7):259-264.
[4]刘爽,张业宽,刘彬.轧机主传动机电耦联扭振系统的动态分岔研究[J].机械工程学报,2010,46(3):83-89.LIU Shuang,ZHANG Ye-kuan, LIU Bin. Dynamical bifurcation study on electromechanical coupling vibration in rolling mill's drive system[J].Journal of Mechanical Engineering,2010,46(3):83 -89.
[5]闫晓强.热连轧机机电液耦合振动控制[J].机械工程学报,2011,47(17):61-65.YAN Xiao-qiang.Machinery-electric-hydraulic coupling vibration Control of hot continuous rolling mills[J].Journal of Mechanical Engineering,2011,47(17):61 -65.
[6]李文,赵慧敏,邓武.变频器驱动异步电动机振动频谱特征分析[J].电机与控制学报,2012,16(8):67-73.LI Wen,ZHAO Hui-min,DENG Wu.Analysis of vibration spectrum characteristics for asynchronous motor driven by inverter[J].Electric Machines and Control,2012,16(8):67-73.
[7]Wang Y N,Gu JC,Chen CM.Real-time tracking of the torsional vibration of an induction motor supplied by distorted voltage sources[J].Electric Power Systems Research,2001,57(3):205-215.
[8] Lockley W E,Driscoll T S,Wharran W H,et al.Harmonictorque considerations applying a6000-HPinduction motor and drive to a high-speed compressor[J].IEEE Transactions on Industry Applications,1995,31(6):1412-1418.
[9] Joseph Song-Manguelle,Jean-Maurice Nyobe-Yome,Gabriel Ekemb.Pulsating torques in PWM multi-megawatt drives for torsional analysis of large shafts[J].IEEE Transactions on Industry Applications,2010,46(1):130 -138.
[10]姚建均,胡胜海,韩俊伟.电液伺服振动台加速度谐波抑制[J].机械工程学报,2010,46(3):22-28.YAO Jian-jun,HU Sheng-hai,HAN Jun-wei.Acceleration harmonic cancellation of electro-hydraulic servo shaking table[J].Journal of Mechanical Engineering,2010,46(3):22-28.
[11]宋琼,朱长春,牛宝良.液压振动台建模与加速度波形失真度分析[J].机床与液压,2008,36(12):81-83.SONG Qiong,ZHU Chang-chun,NIU Bao-liang.Modeling of the hydraulic shaker and analysis of the aceelaration wave distortion[J].Machine Tool& Hydraulcs,2008,36(12):81 -83.

