外载作用下环状周期结构固有频率分裂特性研究

刘 晨， 王世宇,2,3， 高 楠

(1.天津大学 机械工程学院，天津 300350； 2.天津大学 机构理论与装备设计教育部重点实验室，天津 300350；3.天津市非线性动力学与控制重点实验室，天津 300350)

工程领域广泛应用旋转电机、陀螺仪、行星齿轮传动及滚动轴承等基础部件。根据几何构型和受载特征，该类结构可视为受若干外载作用的环状周期结构[1-4]。受周期构型的影响，该类结构通常存在固有频率分裂问题。本文以受外载作用的环状周期结构为对象，研究由外载引起的固有频率分裂现象及其抑制条件。

国内外学者深入探讨了各类因素对环状周期结构自由振动的影响。Huang等[5]建立了弹性支承旋转圆环的振动模型并分析了固有特性，通过分析“静环动载”和“动环静载”这两类典型问题，揭示了科氏加速度对固有频率及振型的影响规律。Cooley等[6]建立了受离散刚度支承的高速旋转圆环的动力学模型，计算了轴对称自由环与非轴对称环在较高转速时的固有特性。林杰等[7]基于波动法研究了旋转圆环的模态特性。此外，Wang等[8]分析了振动波数、磁极数和转速等参数对永磁电机环形转子自由振动的影响。

还有学者研究了固有频率分裂问题。事实上，该问题可追溯至教堂钟的声学研究。为了深刻揭示固有频率分裂规律，Kim等[9]采用摄动法分析了盘形周期结构的分裂规律并给出试验验证。Wu等[10]建立了弹性支承静止环状周期结构的动力学模型，采用摄动法和Galerkin离散获得特征解，揭示了固有频率分裂规律。文献[11]总结了等效对称单元的分组方式与固有频率分裂之间的映射关系。此外，有些学者研究了固有频率分裂的抑制问题，Rourke等[13]建立了含质量缺陷的环状周期结构的自由振动模型，研究了固有频率分裂的抑制问题，指出由质量缺陷引起的非均布构型可改善动力学特性。Wang等[14]提出一种采用分组拓扑构型来抑制固有频率分裂的方法。Liu等[15]研究了拓扑结构与固有频率分裂的影响关系。应当指出的是，上述研究通常以离散质量或刚度来体现周期性。事实上，外载可导致非线性变形，进而显著改变初始应力分布，因此影响固有特性。对于外载如何影响固有频率的分裂行为，目前还未见报道。

本文考虑内外激励共同作用下的环状周期结构的几何非线性变形，拟采用Galerkin离散能量法建立含外载因素的解析动力学模型，研究外载对固有特性的影响，具体将分析拓扑结构与固有频率分裂的映射关系，并提出抑制固有频率分裂的方法。

1 数学建模

1.1 模型描述

在工程实际中，外载通常作为受迫项影响机械系统，但事实上它还产生支撑作用。因此，本文建立了图1所示含外载和支撑刚度的数学模型。其中，图1(a)为固定在弹性基础上受分组对称外载作用的环状周期结构数学模型，图1(b)为外载分布规律。o-rθz为惯性坐标系，极点位于结构的几何形心；v和u分别为圆环中性面上任意一点的径向和切向位移;er,eθ和ez分别为径向、切向及轴向单位矢量。圆环的中性面半径、轴向高度、径向厚度、径向连续支承刚度、切向连续支承刚度以及弹性模量分别为R,c,h,kv,ku和E。外载共有N1组，每组含N2个等间隔分布的外载。θij为第i组第j个外载的位置角，其中θij=θi+αj，θi=2π(i-1)/N1，αj=(j-1)α，α为组内相邻外载之间的夹角。第i组中的第j个外载记为Fij，为位置的函数，且每个外载与圆环径向的夹角均为β，离散刚度kmij与外载有相同的位置与径向夹角，同时为位置的函数。

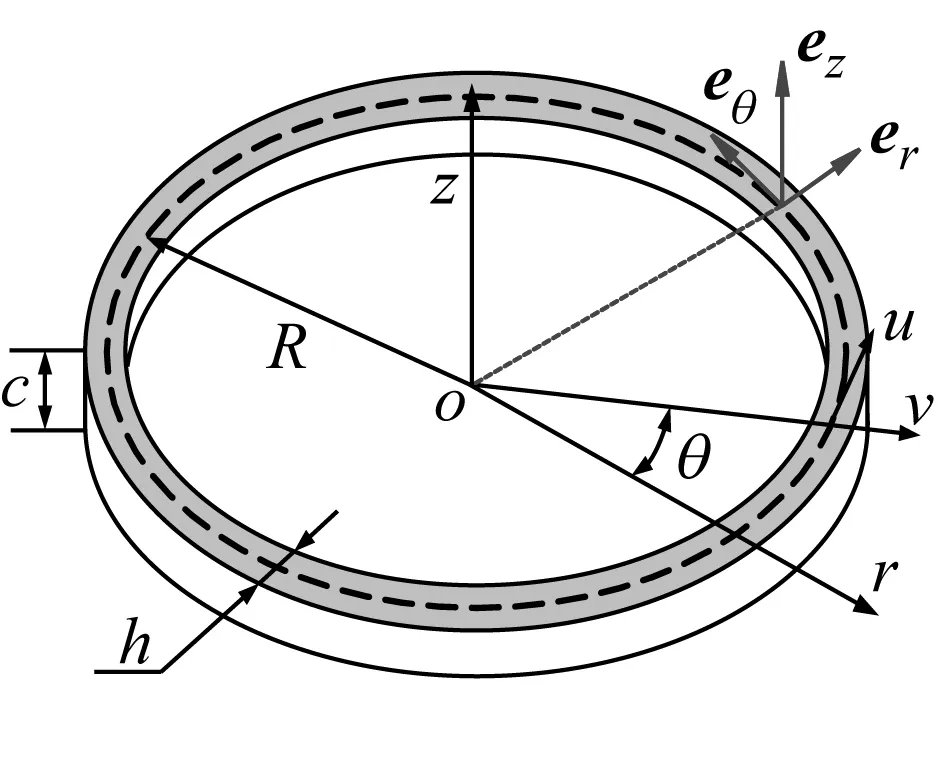
(a)

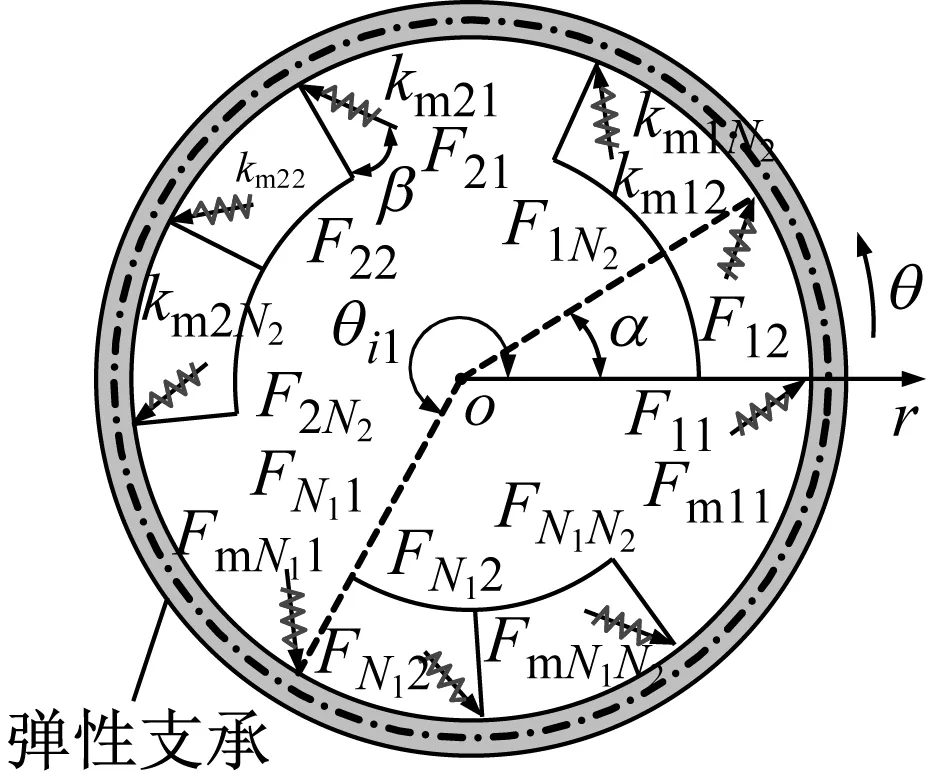
(b)图1 受分组对称外载作用的环状周期结构数学模型Fig.1 Schematic of RSPS subjected to grouping symmetrical external loads

1.2 能量分析

采用Euler-Bernoulli梁假设[16]，并应用能量法建立数学模型。在图1所示惯性坐标系下，圆环中性线上任意一点(r,θ)处的位置矢量可表示为

r=(R+v)er+ueθ

(1)

1.2.1 动能

在惯性坐标系下，圆环的动能可表示为

(2)

式中,d为材料密度，且

(3)

1.2.2 外载功

作用于圆环上任意点(r,θ)处的外载可表示为

(4)

式中:fm为幅值;δ为Dirac函数。外载功可表示为

(5)

1.2.3 势能

在平面应变状态下，(r,θ)处的切向应变为[17]

εθ=εθ0+(r-R)εθ1

(6)

其中

则应变能可表示为

(7)

式中:I为圆环截面的主惯性矩(I=ch3/12);圆环截面积A=ch。

连续和离散支承刚度的势能可分别表示为

(8)

(9)

其中

(10)

式中，km为幅值。因此，系统的总势能为

U=U0+Us+Um

(11)

1.3 数学模型

根据Hamilton原理

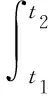
(12)

同时应用非线性无延展假设[18]

(13)

并将式(2)、式(5)和式(11)代入式(12)，可得

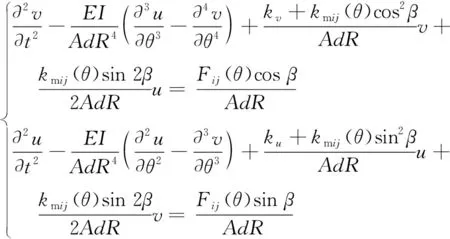
(14)

根据式(13)，经多次逼近可将径向和切向位移分别用时变广义坐标An(t)和Bn(t)表示为

v(θ,t)=An(t)cosnθ+Bn(t)sinnθ-

(15)

(16)

式中,K=(n-1/n)2且n≥2，n为波数。

将式(15)和式(16)代入式(14)，分别乘以An(t)和Bn(t)的权函数

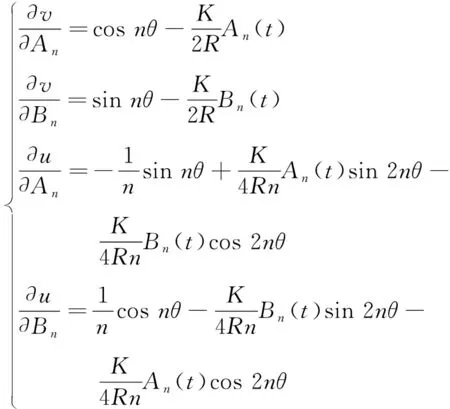
(17)

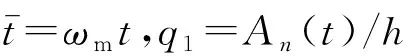
(18)

其中

A6=n2kmcos2β-kmsin2β，

式中：Kc为定常刚度矩阵；Kk为支承刚度矩阵；Kf为外载刚度矩阵。

由式(18)可知，通常作为受迫项的外载出现在动力学方程的刚度系数中，因此必然影响固有特性。事实上，外载使结构受预应力作用，进而影响了刚度分布规律，因此导致固有特性的改变。

2 固有频率分裂特性分析

2.1 固有频率

为求解固有频率，假设

(19)

式中,ωn为固有频率，将式(19)代入式(18)可得特征方程

(20)

解得

(21)

其中

2.2 固有频率分裂规律

(25)

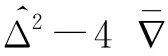
为了深入分析离散外载和刚度对固有频率的影响，本文给出以下4种典型情形：① 自由模式(fm=km=0)；② 纯外载模式(fm≠0,km=0)；③ 纯刚度模式(fm=0,km≠0)；④ 复合模式(fm≠0,km≠0)。

2.2.1 自由模式

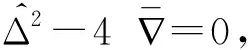
表1 固有频率及其分裂规律(fm=km=0)Tab.1 Natural frequencies and splitting conditions (fm=km=0)

表1中

2.2.2 纯外载模式

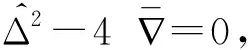
表2 固有频率及其分裂规律(fm≠0,km=0;l,l′为正整数)Tab.2 Natural frequencies and splitting conditions (fm≠0, km=0; l and l′ are positive integers)

表2中

2.2.3 纯刚度模式

表3 固有频率及其分裂规律(fm=0,km≠0;l,l′为正整数)Tab.3 Natural frequencies and splitting conditions (fm=0, km≠0; l and l′ are positive integers)

表3中

2.2.4 复合模式

表4 固有频率及其分裂规律(fm≠0,km≠0;l,l′为正整数)Tab.4 Natural frequencies and splitting conditions (fm≠0, km≠0; l and l′ are positive integers)

综上可知，可利用振动波数与分组数的关系，初步判定固有频率是否分裂，然后根据组内匹配关系最终确定是否发生分裂现象。由于外载与刚度的分布特征相同，因此除影响程度不同之外，固有频率是否分裂的判定条件完全相同。因此，调整分组参数与外载可控制频率分裂行为。

3 仿真分析

3.1 基本参数

表5为环状周期结构的基本参数，如不作特殊说明，均使用表5中的参数进行仿真计算，具体将根据表5和式(21)分析4种模式及其他参数对固有频率分裂行为的影响。

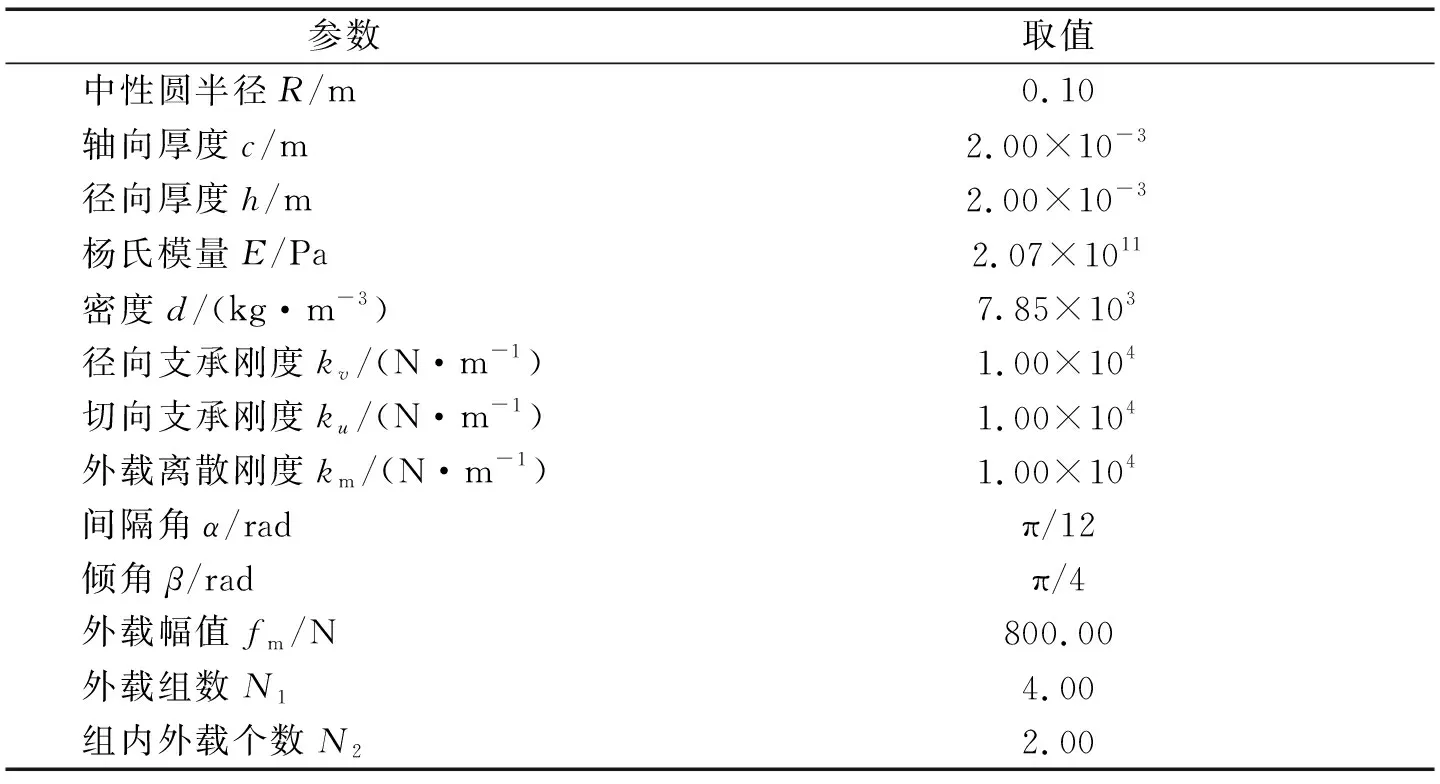
表5 环状周期结构基本参数Tab.5 Parameters of a RSPS

3.2 离散外载影响

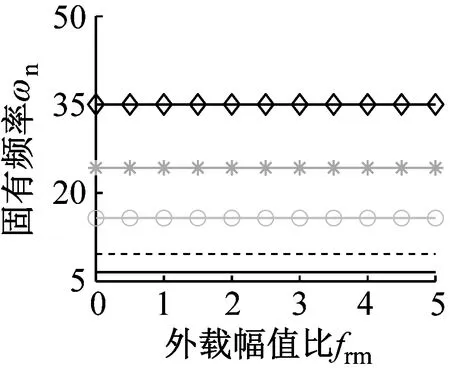
图2描述了波数和外载对固有频率的影响，其中第n阶振型对应的固有频率为ωn1和ωn2(ωn1≤ωn2)，rω(rω=ωn2-ωn1)表征固有频率的分裂程度。

(a) 模式①

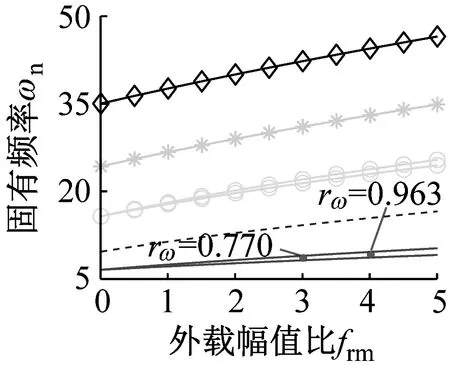
(b) 模式②

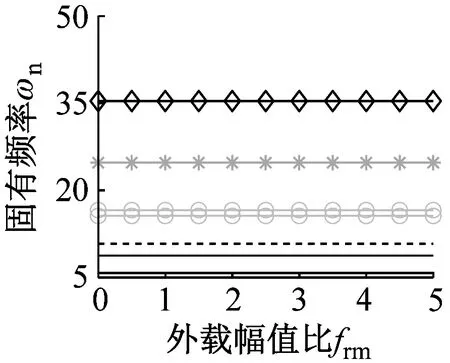
(c) 模式③

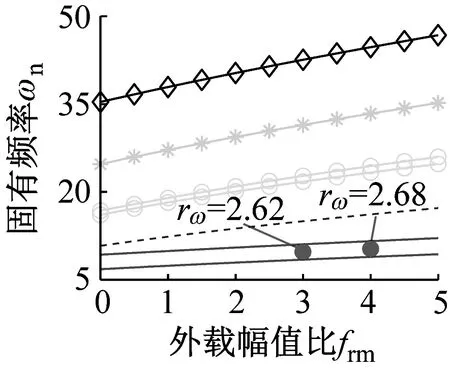
(d) 模式④图2 固有频率随外载变化规律Fig.2 Natural frequencies versus external load ratios

由图2可知，模式①的固有频率不分裂，模式②、模式③和模式④出现固有频率分裂且分裂规律相同。对比图2(a)与图2(b)可知，外载影响固有频率，且随着外载逐渐增大，固有频率随之增大。这表明在弹性变形范围内，增加外载可提高固有频率。观察该组参数下的固有频率分裂趋势可知：增加外载可增大分裂程度。图2(b)和图2(d)给出了离散刚度与分裂程度的关系。以n=2为例，当frm=3时，模式②和模式④的分裂程度为rω=0.77与2.62，显然模式④的分裂程度大；当frm=4时，模式②和模式④的分裂程度为rω=0.96与2.68，表明模式④的分裂程度更大。

3.3 离散刚度影响

图3描述了波数和离散刚度比对固有频率分裂行为的影响。可以看出，图3(b)～图3(d)的分裂规律相同。由图3(c)可知，增大刚度将增加固有频率分裂程度。比较图3(c)与图3(d)可知，在当前参数组合下，外载可降低固有频率分裂程度。

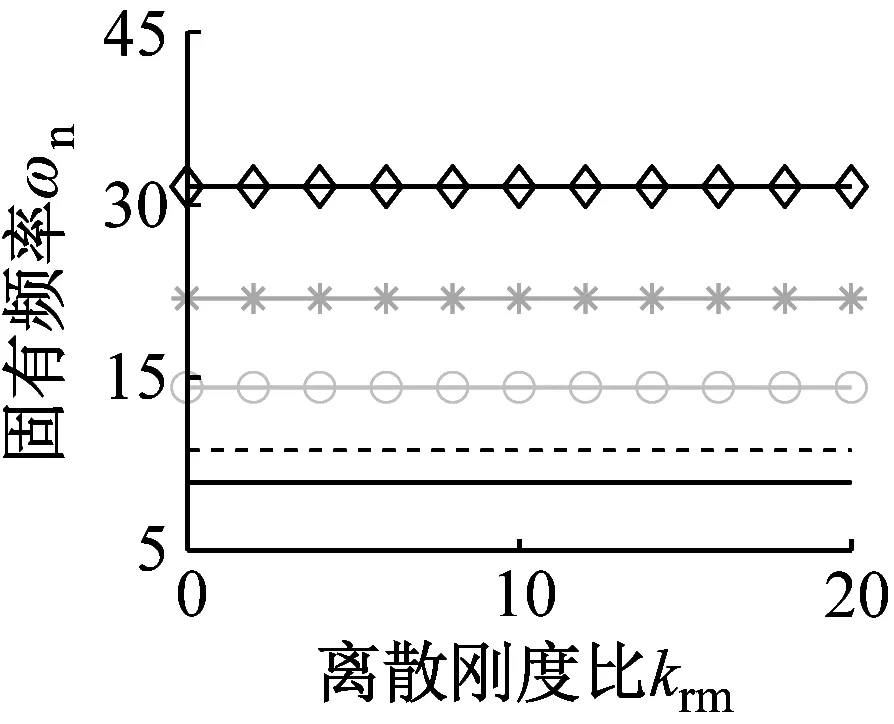
(a) 模式①

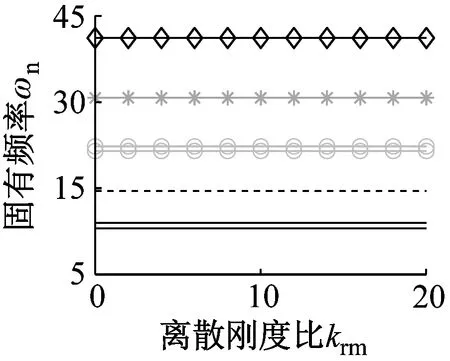
(b) 模式②

(c) 模式③

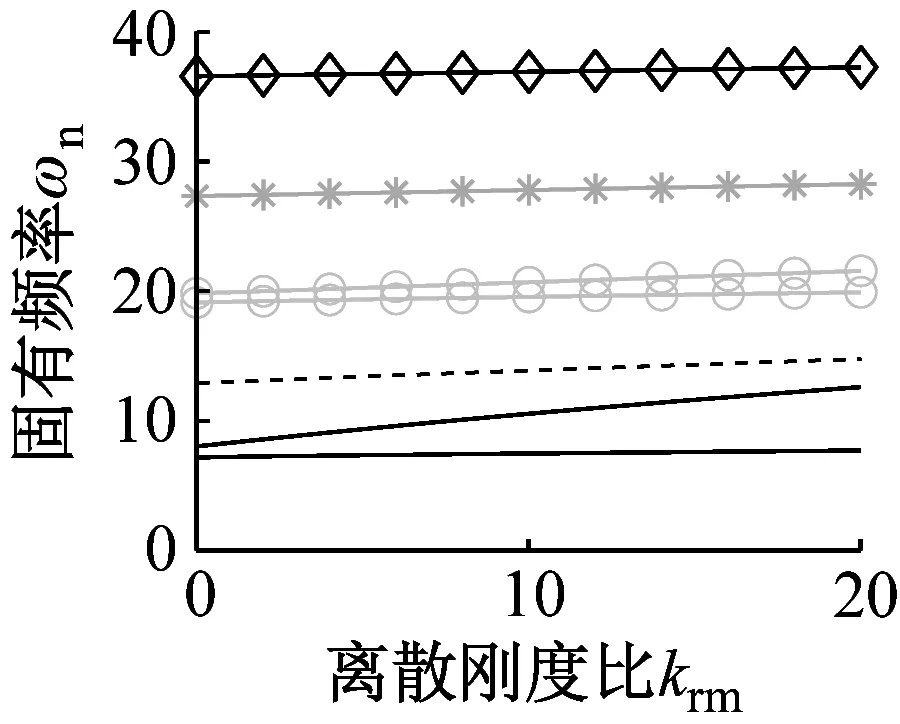
(d) 模式④图3 固有频率随离散刚度比变化规律Fig.3 Natural frequencies versus increasing stiffness ratios

3.4 倾角影响

图4描述了波数和倾角对固有频率的影响。对于模式②～模式④而言，随着倾角的增大，固有频率均有所下降。比较模式②和③可知，仅考虑外载模式的固有频率下降较显著，此时外载的施加方向由径向逐渐变为切向。对比图4(b)与图4(d)，发现当n=4时，随着倾角由π/4增至π/2，分裂程度分别由rω=0.52与0.91变为rω=0.91与0.97，可知模式④的分裂程度变化较小，表明当外载与离散刚度共同作用时，倾角对分裂程度的影响较小。

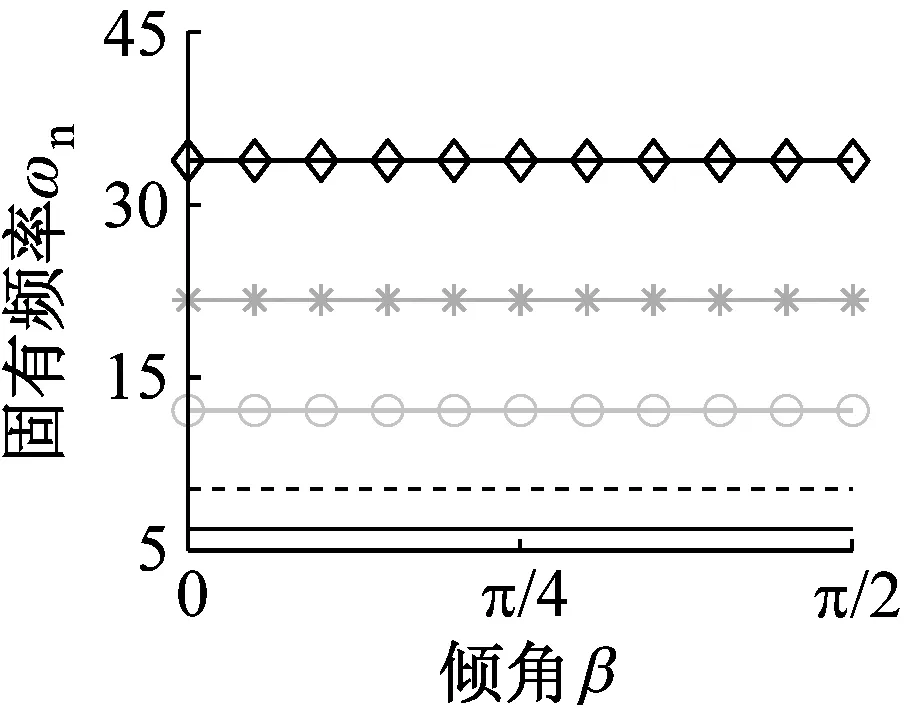
(a) 模式①

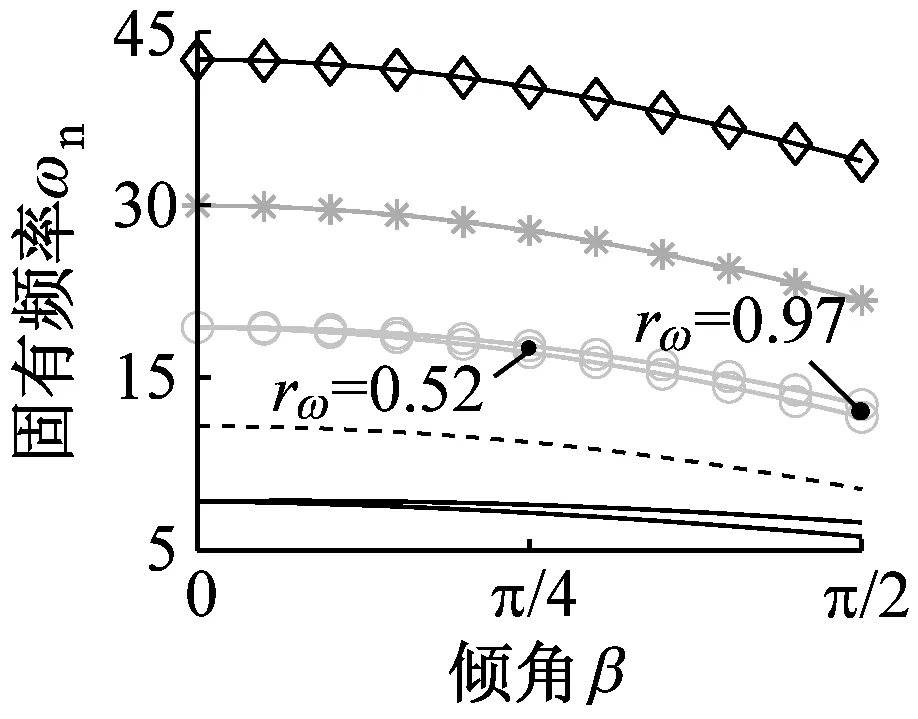
(b) 模式②

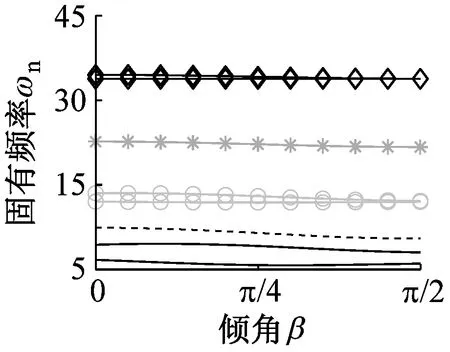
(c) 模式③

(d) 模式④图4 固有频率随倾角变化规律Fig.4 Natural frequencies versus increasing orientation angles

3.5 间隔角影响

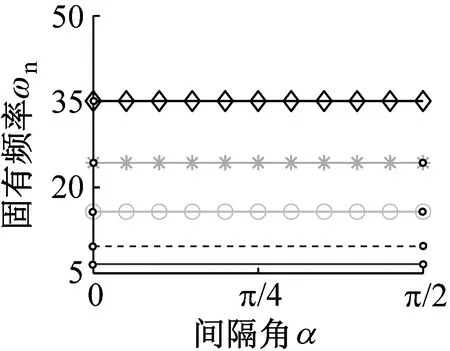
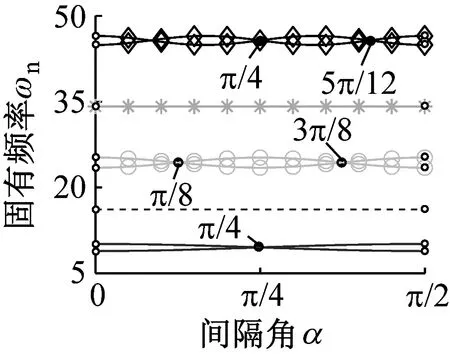
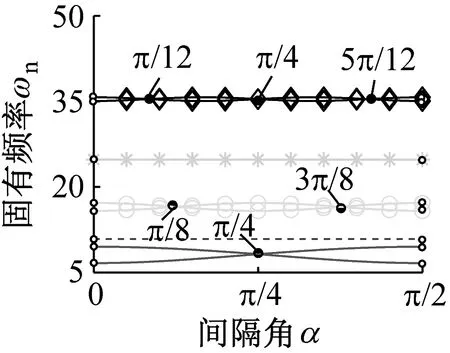
图5描述了波数和间隔角对固有频率的影响。当间隔角α=0时，对于模式②～模式④的不同波数，均存在固有频率分裂现象。随着间隔角的增加，分裂固有频率出现波动现象，且在某些特殊位置不再分裂(为便于观察，图中的固有频率分裂抑制位置用“·”标注，并给出了相应的角度)。因此，改变分组方式可调整分裂行为。

(a) 模式①

(b) 模式②

(c) 模式③

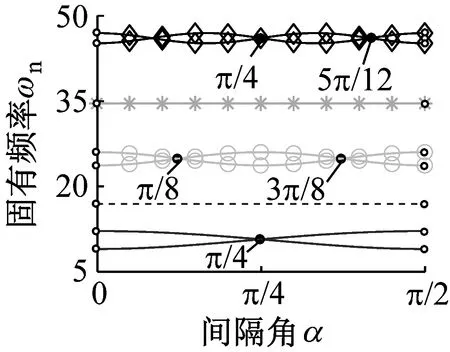
(d) 模式④图5 固有频率随间隔角变化规律Fig.5 Natural frequencies versus interval angles

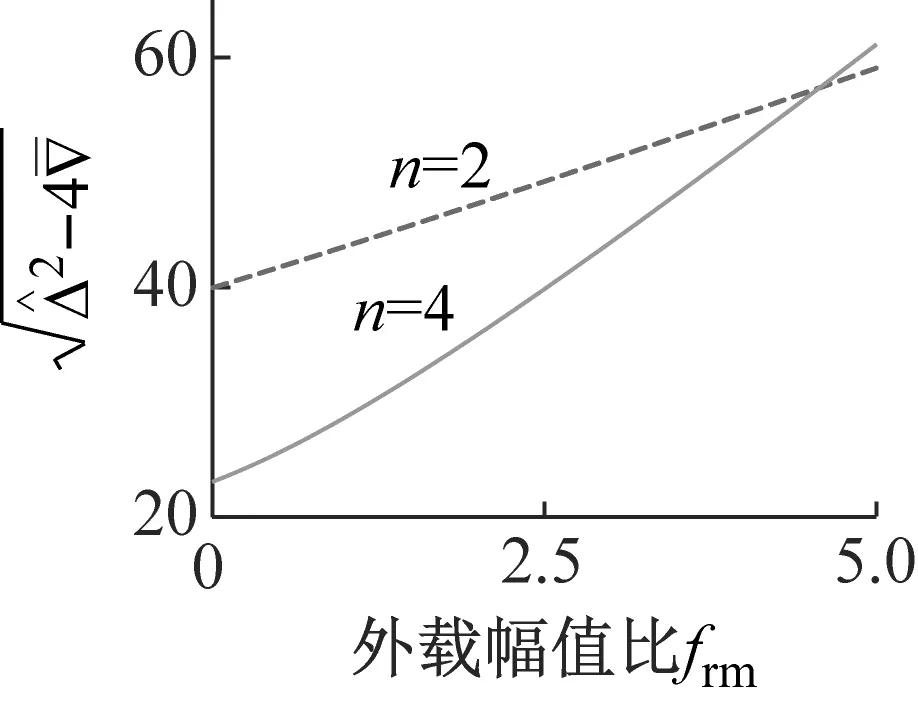
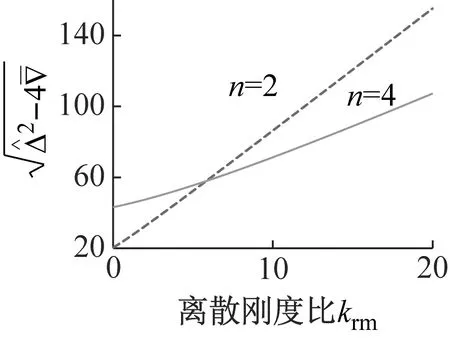
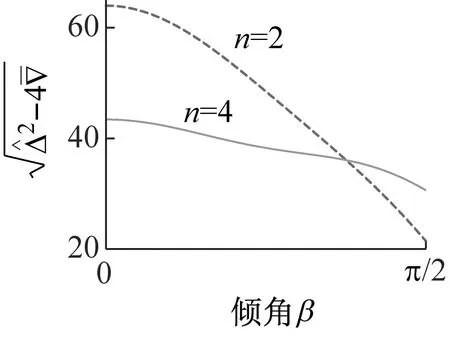
3.6 固有频率分裂程度变化规律

(a)

(b)

(c)

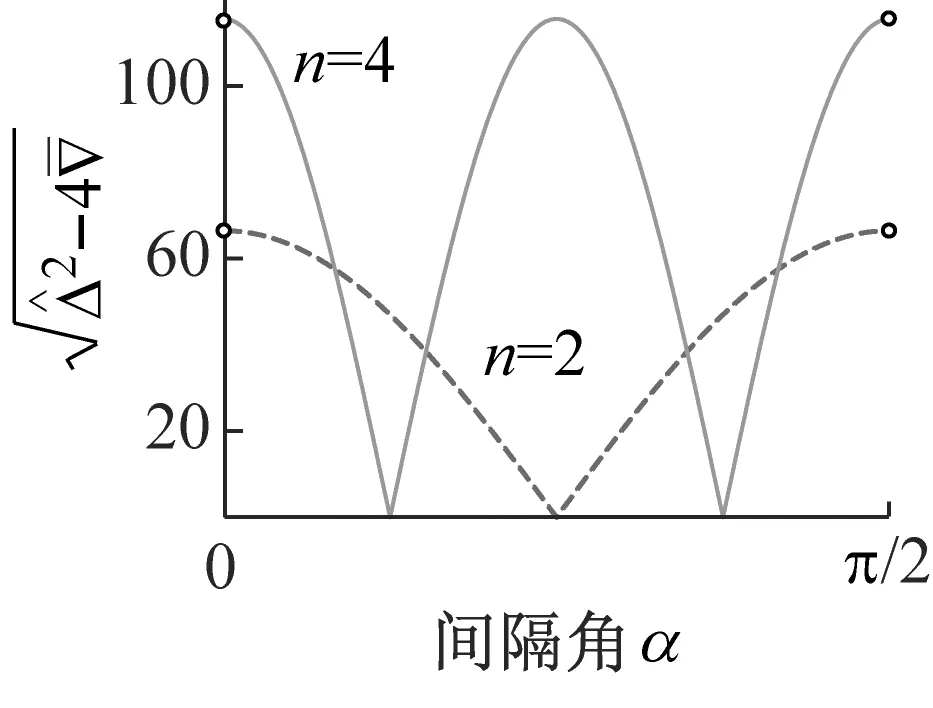
(d)图6 不同参数下固有频率分裂程度Fig.6 Natural frequency splitting versus different parameters

3.7 固有频率分裂抑制实例

表6给出组数、组内个数、间隔角及波数等不同参数匹配下周期结构的固有频率。

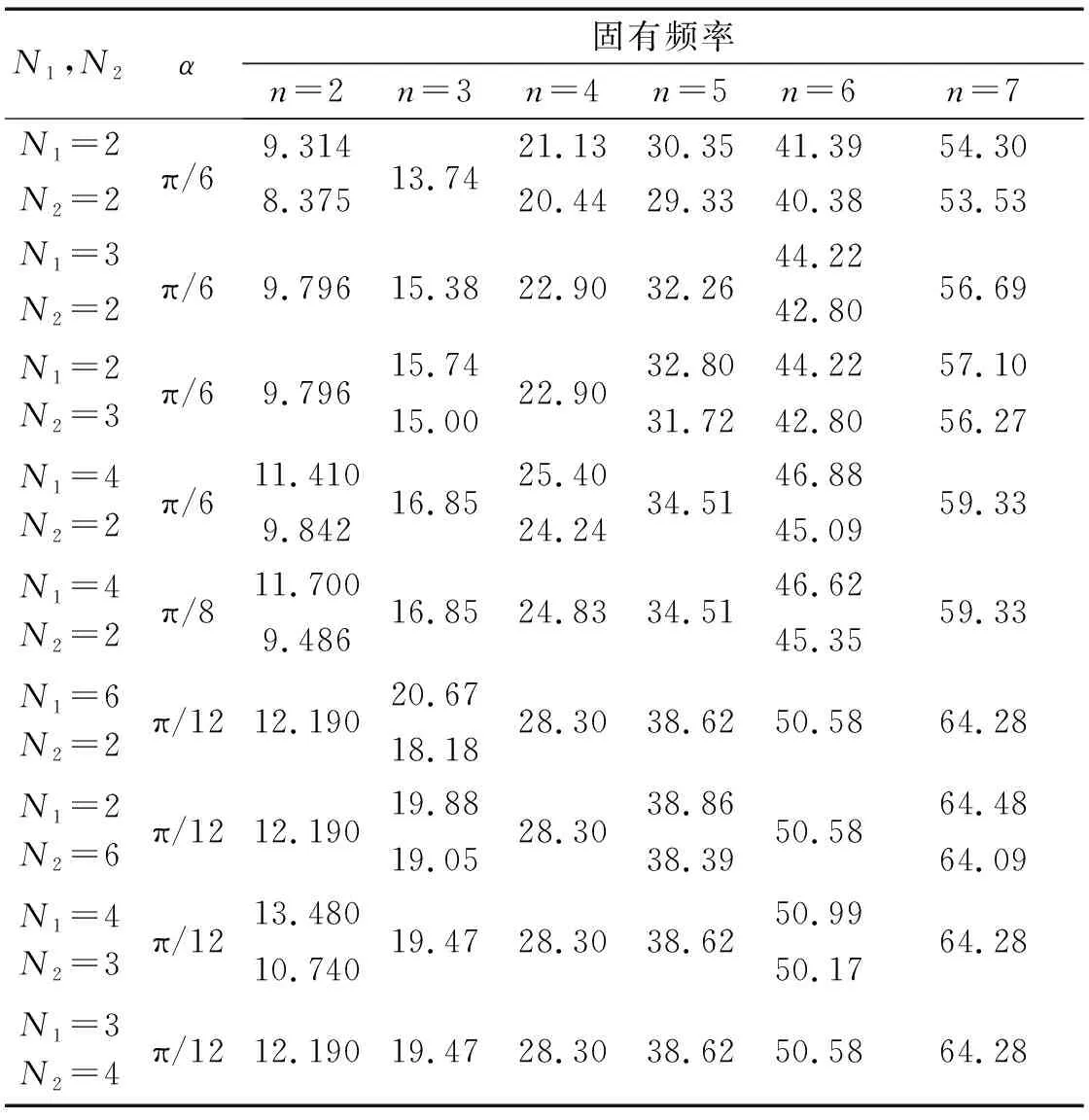
表6 环状周期结构固有频率Tab.6 Natural frequencies of the RSPS

由表1～表4可知，若2n/N1不为整数，则对应的固有频率必定重合，该结论与组内的外载分布特征无关。本文以参数组合{N1，N2，α，n}={4，2，π/6，4}和{4，2，π/8，4}为例，在不改变{N1，N2，n}的前提下，将间隔角调整为π/8。若不考虑计算误差，则原分裂固有频率(25.40，24.24)变为重合频率(24.83，24.83)。在不改变波数和间隔角的前提下，通过改变分组方式也可抑制频率分裂。以参数组合{2，3，π/6，3}和{3，2，π/6，3}为例，将分组方案{N1，N2}={2，3}调整为{3，2}，原分裂固有频率(15.74，15.00)变为重合固有频率(15.38，15.38)。若不改变外载组数N1，通过调节组内外载的数量和间隔角也可抑制频率分裂。通过对比参数组合{4，2，π/6，4}与{4，3，π/12，4}可发现，在不改变分组数N1的前提下，如果将组内分布参数{N2，α}调整为{3，π/12}，原分裂频率(25.40，24.24)将变为重合频率(28.30，28.30)。在保证组内外载个数N2、间隔角α及波数n不变的前提下，可改变外载组数以使频率重合。例如，若参数组合为{4，2，π/6，2}和{3，2，π/6，2}，可将外载的组数{N1}调整为{3}，原分裂频率(11.41，9.842)即变为重合频率(9.796，9.796)。上述结果表明，改变外载的构型及特征参数可显著抑制固有频率分裂。

4 结 论

本文研究了分组对称外载荷对环状周期结构固有频率分裂特性的影响。主要工作及结论如下：

(1) 应用非线性无延展假设，采用Hamilton原理建立了受分组对称外载作用的环状周期结构的解析动力学模型，该模型计入了均布和分组对称的外载及支撑刚度。

(2) 外载和刚度均影响固有频率的数值及其分裂程度。若2n/N1不为整数，无论参数如何选取，固有频率均不分裂；若2n/N1为整数，则固有频率是否分裂取决于组内参数的匹配关系。

(3) 揭示了外载和刚度的倾角、间隔角等参数对固有频率的影响规律，具体分析了4种典型模式下基本参数影响固有频率的规律，还提出一种抑制固有频率分裂的方法。