直升机旋翼/机身动力反共振隔振器的优化设计

李园园， 陈国平， 王　轲

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京　210016)



直升机旋翼/机身动力反共振隔振器的优化设计

李园园， 陈国平， 王轲

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京210016)

为提高直升机旋翼/机身反共振隔振器的隔振效率，对直升机主减隔振系统进行了优化设计。通过灵敏度分析，确定了以前后柔性梁的厚度和配重的密度作为优化设计变量，接着采用遗传算法对隔振效率和配重动能进行优化，考虑到仿真模型直接调用优化算法的计算效率较低问题，建立了基于响应面方法的优化近似模型。结果表明：优化后模型的某一阶反共振频率与激励频率一致，配重振动加大，力传递率下降，隔振效率大幅度提高。优化设计提高了动力反共振隔振器的隔振性能，可以为直升机隔振器的设计提供一定的指导。

直升机；反共振隔振器；响应面；优化设计

直升机在开展民用和军事行动等特殊任务上发挥着重要的作用，然而，由于动力学环境的复杂性，发动机和主旋翼剧烈振动，这些振动与冲击严重影响着机组人员的乘坐舒适性、设备的使用性和工作可靠性，降低部件的疲劳寿命。因此，降低直升机振动问题迫在眉睫[1,2]。

国内外学者为减轻直升机振动水平进行了大量的研究工作。针对直升机旋翼系统中隔振系统静变形不能太大与激励频率低这一矛盾，早在1963年Flannelly就提出了动力反共振隔振器(Dynamic Antivibration Isolator，DAVI)理论，这一新型的隔振器巧妙地结合了隔振和吸振，具有隔振特点和吸振特征，成功解决了直升机的振动问题[3-4],之后，此类隔振器趋向多样化，顾仲权[5]对该种隔振器进行了深入的研究，并提出了以弹性轴承支撑为主的DAVI，隔振效率高，几乎无噪声。李五洲[6]将DAVI理论应用于某型机，利用有限元软件分析了动力反共振隔振装置的隔振原理，重点分析了反共振频率与隔振器参数的关系。单一的DAVI主要隔离直升机在垂向激励下的振动，为此，法国学者将单项DAVI与聚焦柔性巧妙结合研制成SARIB隔振方案，能够隔离升力方向和旋翼旋转平面内的激振力。黄传跃[7]对一种新型旋翼/机身隔振装置(NRFVI)进行了静动力学特性分析，该隔振装置将弹簧式结构发展成联合梁式，兼具柔性隔振和反共振隔振。之后的学者运用动力反共振原理对机械式反共振隔振器进行不同的改进，邓旭东[8]提出了一种采用橡胶弹性扭管的新型高性能主减隔振系统，并在他的硕士论文中阐述了不同类型DAVI的原理、应用及隔振效率，如机械式DAVI，液体式DAVI和周期层合式黏弹DAVI。

上述研究中，主要通过改进不同类型的隔振器元件来提高隔振效率，而Joseph[9]从隔振元件的固有模态入手，分析了固有模态和隔振频带之间的关系，运用模拟退火算法对隔振器进行优化，从优化的角度提供了一种新的设计思路。

本文针对直升机的振动问题，从隔振原理出发建立了工程样机的动力学模型，对模型中的设计参数进行灵敏度分析，找出影响隔振效率和配重动能较大的参数定为优化设计变量，采用拉丁方试验设计拟合得到响应面近似模型，运用遗传算法分别进行单目标和多目标优化，为直升机主减隔振系统的设计提供理论依据。

1　动力反共振隔振原理

图1为一种基本的弹簧式反共振隔振装置[5]，它是在常规隔振器基础上附加惯性元件构成的，其中，M1、M2，m分别为隔振对象质量、加载处质量和配重的质量，A、B为ABCD梁的两个支点，C为梁的质心，r为两支点之间的距离，a为梁质心到B支点的距离，R为支点A到配重质心的距离，记ABCD梁的质量及绕质心C的转动惯量分别为mr、Jr。该力学模型的动能T，势能V和耗散函数E分别为：

(1)

(2)

(3)

将方程(1)～(3)代入Lagrange方程

(4)

得到：

(5)

(6)

(7)

当TD=0时，得到反共振频率为：

(8)

由式(7)、(8)可以看出，运动传递率与隔振对象和配重的质量、刚性杆的参数以及刚度系数有关，而反共振频率与隔振对象质量和加载处质量无关。

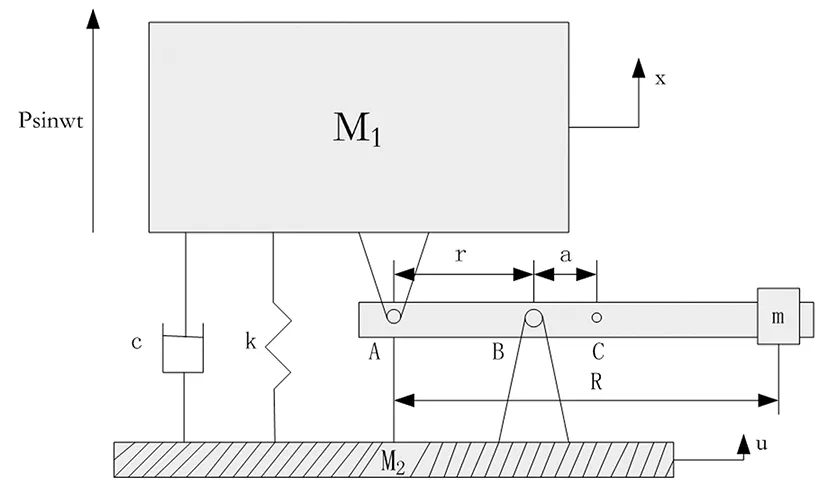
图1　弹簧式DAVI简图Fig.1 The Spring DAVI sketch

2　动力反共振隔振器的动力学建模

本文所设计的隔振模型是为更好的隔离直升机在某一阶频率下的桨毂交变力和力矩。已知直升机的振源主要是竖向定频激励，假如激励频率在25 Hz时直升机振动最为剧烈，则隔振器在25 Hz时应接近其某一阶反共振频率，这样，当外激励频率接近25 Hz时，原振动位置的振幅就会减小，达到局部隔振的目的。

鉴于此，以直升机主减系统的原始模型为依据，在能简单真实的反映结构惯量特性和刚度特性的前提下，对旋翼、主减和机身等做适当的简化，运用动力反共振隔振原理，结合聚焦式隔振和柔性隔振，通过对关键部件进行调整，模型具有很好的隔振效果。平面结构简图如图2所示。

图2中，各部件之间的连接均采用铰支，主减速器上固联一个具有一定弹性的防扭盘，主减速器与机身之间通过防扭盘进行力和力矩的传递，因此，防扭盘的弹性会对隔振效率产生一定的影响。在进行动力学建模时，将柔性梁和防扭盘之间的联接件用弹簧和阻尼器等效，防扭盘和机身之间等效为刚度系数很大的弹簧联接。前后质量块的质量和共振梁的长度因整机参数的要求而不同。该聚焦柔性动力反共振隔振器前后共有4个单一的DAVI，当桨架受垂向激励时，四根斜支撑将垂向力传递到柔性梁上，引起共振梁振动，从而使质量块具有一定的动能，完成吸振功能。当桨毂受到旋翼水平面内的交变力激励时，桨架在柔性梁的支撑下以主减底部为振动节点偏摆，由于偏摆的模态频率较低，向机身传递的交变力就会减小，从而降低振动水平。在振动过程中，共振梁、柔性梁和质量块之间存在力的平衡关系：FA+FB+Fg+FE=0，其中，FA为支点A的支反力，FB为B点的作用力，Fg为质量块的惯性力，FE为作用在柔性梁和主减速器之间的作用力，适当调整FA可使隔振器的力传递率为0[6]。

由于机体的非对称性，在垂向激励下桨架会前倾，造成机体的俯仰运动，根据Ⅱ类DAVI的特性[10]，假设系统受垂向的激励力和绕垂向转动的激励力矩的作用，位移分别为z和θ，设四根柔性梁的竖向位移分别为za,zb,zc,zd，建立图2系统的动力学模型。

系统动能包括主减速器动能、前后质量块动能、柔性梁以及斜支撑的动能，分别为：

则系统的总动能T*为

T*=T1+T2+T3+T4

(9)

系统的位能U*为：

(10)

系统的耗散函数E*为：

(11)

为研究该隔振器的动力学特性，建立了该装置的有限元模型，在进行频响函数分析时，设置模型的整体阻尼系数为0.02，假如隔振器受到幅值A=20 N，频率在1～39 Hz范围内的垂向正弦激励，力传递特性如图3所示。

图3　支反力频响函数曲线Fig.3 The FRF curve of constrain forces

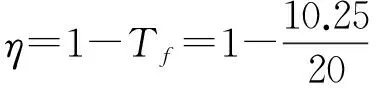
3　动力反共振隔振器的优化

3.1灵敏度分析

灵敏度分析是优化设计实现的重要步骤，在隔振器的众多部件中找出影响隔振效率的敏感部件，有针对性的进行优化设计，有助于提高优化效率。灵敏度分析的基本思想是优化模型的目标函数和约束条件对设计参数变化的灵敏性[11-12]，即：

(12)

式中：uj为优化模型的目标函数和约束条件，xi为设计变量。本文选取动力反共振隔振器的斜支撑杆半径r、前柔性梁的厚度t1、后柔性梁的厚度t2、配重的密度ρ以及防扭盘厚度d为设计变量，以隔振器的隔振效率和配重的动能为目标函数，计算目标函数在25 Hz时对设计变量变化的灵敏度，结果如表1所示。

当灵敏度值大于零时，目标函数值会随着设计变量值的增大而显著增加，当灵敏度值小于零时，目标函数值会随着设计变量值的增大而减小，灵敏度值的正负只表示目标函数值随设计变量值变化的灵敏度方向[13]。由表1可以看出，前后柔性梁的厚度t1和t2以及配重的密度ρ对隔振效率和配重动能的影响最大，而防扭盘厚度d和斜撑杆半径r的影响相对较小，因此，在后续的优化中，以前后柔性梁的厚度和配重的密度作为优化设计变量进行隔振效率和配重动能的优化，其初始值及取值上下限如表2所示。

表1　灵敏度分析

表2　设计变量的取值范围

3.2反共振隔振器的优化

3.2.1全局近似函数的构建

在优化过程中，如果仿真模型直接调用优化算法，迭代时间会很长，优化效率低下，此外，优化过程中仿真参数的变化和设计变量的取值不合理容易使单次计算失败，导致整个优化过程终止[14]。因此，用描述样本点与结构响应特征之间的关系构建代理模型代替真实目标函数进行优化，可以显著提高优化效率。本文采用响应面法拟合得到全局近似模型[15]。

经典响应面法是以多项式表示的一阶或二阶模型，其中以二阶模型最为常用，适用于线性特征较强的模型，基本形式如下：

(13)

式中：xi，xj分别为第i个和第j个设计变量，m为总的设计变量数，αi，αii为待定系数，ε为误差项。针对不同的模型，上述多项式可以取不同的阶数。

将设计变量和真实响应值代入(14)式，依据最小二乘原理通过回归分析可以确定多项式系数α，写成矩阵的形式为：

α=(XTX)(XTf)

(14)

3.2.2模型精度检验

为确保模型的拟合精度，常用决定系数R2及均方根误差RMSE检验代理模型，当R2值接近1，RMSE值接近0时说明代理模型的精度较高。表达式分别如下[15]：

(15)

(16)

(17)

(18)

基于上述理论，本文以配重的密度和前、后柔性梁的厚度为3个设计变量，采用拉丁超立方试验设计在整个设计空间中进行抽样，获得45个样本点，然后通过有限元分析获得支反力和配重动能的仿真数据，采用最小二乘法分别计算2个目标函数的回归系数矩阵，构成全局近似模型，表达式如下:

F(X)=27.948 8x33x1+36.55x13+0.835 8x23-

23.992x33-9.4997x12x3-28.572x12-

14.053 6x22+0.750 3x32-7.178 3x1x2-

27.495 2x1x3+25.284 6x2x3+8.603 1x1+

5.047 6x2+12.194x3+8.151 5

(19)

E(X)=12.1x14+14.367 2x24-20.450 7x34-

33.021 9x13-21.382 3x23+28.278x33+

23.285 6x12x3+27.649 8x12+6.531 3x22-

6.550 3x32+5.493x1x2-37.163x1x3+1.69x2x3-

2.988x1+0.1x2+9.021 4x3+1.957 7

(20)

响应面模型如图4和图5所示。

图4　支反力的响应面模型Fig.4 Response surface of the counterforce

图5　配重动能的响应面模型Fig.5 Response surface of the kinetic energy

由于在代理模型的构建过程中有3个变量，为画出三维响应面图形，本文将其中一个变量设为常数。

上述两个代理模型的决定系数R2分别为0.966 3和0.986 5，RMSE的值分别为0.038 4和0.028 3，说明所建近似面质量较高，能够提供较好的全局预测。

3.2.3优化

本文将隔振效率的优化转化为隔振器支反力的优化，使吸振器动能和支反力在25 Hz下的激励频率下分别达到最大和最小，以使吸能增加隔振效率提高，其数学模型描述为：

(21)

式中：X表示优化设计变量t1、t2和ρ，Xu、Xl分别表示设计变量的上下限，ω0为反共振频率，本文取25 Hz，F、E分别表示支反力与配重动能。需要注意的是，由于动能要求取极大值，因此对动能的目标函数乘以-1，将问题转化为求动能相反数的极小值。

在优化过程中，由于各个变量的变化范围不尽相同，为便于分析比较，将所有变量进行无量纲化处理，设第i个变量的实际变化范围是[p1ip2i]，i=1,2,3，则无量纲化的变化区间为：

(22)

经变换，变量pi的变化范围转化成新变量xi的变化范围[01]。于是模型的初始设计变量均变为“0.5”。

对所建的动力反共振隔振器有限元模型进行频响分析，提取模型在25 Hz处的速度和约束反力值，计算配重动能，生成构建代理模型的初始样本点，构建目标函数的响应面模型，然后调用Matlab中的遗传算法并结合Nastran动响应计算，可以获得单目标优化的最优解及多目标优化的Pareto前沿。优化结果如表3所示。

表3　优化结果

由表3可以看出，针对支反力最小的单目标优化有效的减小了支反力的幅值，其大小由10.245 N减小为3.365 N。针对配重动能的单目标优化的目的是使配重在25 Hz处剧烈振动，从而最大程度的吸收振动能量，优化后的动能提高到6.663×10-6J，然而此时的支反力却达到16.25 N，这表明在保证动能提高的同时，很难减小支反力的大小。由多目标优化的Pareto解集可以看出，支反力和配重的动能出现同时减小或增大的解， 而本文设计隔振器的目的是减小支反力(提高隔振效率)的同时增加配重的吸能，因此，为实现上述优化目标，本文在优化模型(21)的基础上继续优化，将上述支反力的优化结果定为下一步优化的最大值，使最终优化的支反力小于3.365 N，将动能相反数的最小值定为目标函数来提高配重的动能，从而达到设计目的，其优化模型如下所示：

(23)

式中：F0(X)为上一步优化的支反力值3.365 N，其他各参数定义如式(21)所示，最终的优化结果如表4所示。

表4　最终优化结果

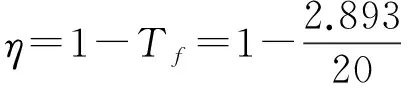
图6　优化前后的支反力频响函数曲线对比Fig.6 The Contrast of reaction forces FRF curve before and after optimization

由图6可以看出，优化后的隔振器在25 Hz处为其反共振频率，此时力的传递率大幅度降低，配重动能增加，隔振效率提高。

然而，当直升机受到幅值为200 N的竖向正弦激励时，该隔振器在优化前传到机身的力为102.885N，隔振效率为48.56%，传到机体的总能量为0.021 2 J，配重吸收的能量为4.5×10-4J，吸能比为2.12%，而在优化后，机身在该激励下受到的载荷仅为30.934 N，隔振效率达到84.53%，提高了74.07%，此时配重吸收的能量为5.531×10-4J，吸能比为2.6%，提高了22.64%。由于在两种不同载荷作用下隔振效率和吸能比的提高量接近，从而验证了上述优化过程的可行性，同时也说明了隔振效率与激励大小无关。

4　结　论

(1) 隔振效率是直升机主减隔振系统的重要指标，本文从优化的角度对主减隔振系统进行设计，提高了隔振效率。

(2) 基于灵敏度分析和响应面方法对动力反共振隔振器的隔振效率和配重动能进行了优化。在优化过程中，运用灵敏度分析避免了设计变量选择的盲目性，采用响应面法构造目标函数的近似模型，减小了优化计算的工作量，提高了计算效率。

(3) 根据设计目标对最优解集进行决策分析，找出使隔振效率提高吸能增多的解，结果表明：优化后的隔振效率有了极大的提高，同时吸能比也有一定程度的提高，达到了设计目的，可以为降低直升机振动提供技术指导。

[1] Phuriwat A I. Semi-active control of helicopter vibration using controllable stiffness and damping device[D]. United States：The Pennsylvania State University, 2002.

[2] Ganguli R. Optimum design of a helicopter rotor for low vibration using aeroelastic analysis and response surface methods[J]. Journal of Sound and Vibration, 2002, 258(2):327-344.

[3] Cheung Y L, Wong W O. Design of a non-traditional dynamic vibration absorber[J]. Journal of the Acoustical Society of America, 2009, 126(2): 564-567.

[4] Flannelly W G. The dynamic anti-resonant vibration solator [C]//Proc of 22ndAnnual AHS National Forum. Washingten DC, 1966: 152-160.

[5] 顾仲权. 动力反共振隔振[J]. 噪声与振动控制,1989,12(6):36-40.

GU Zhong-quan.Power anti-resonance isolation[J]. Noise and Vibration Control, 1989, 12(6):36-40.

[6] 李五洲. 反共振隔振装置隔振原理分析[J]. 直升机技术, 2004, 8(1):6-8.

LI Wu-zhou. The isolation principle analysis onanti-resonance isolator[J]. Helicopter Technology, 2004, 8(1):6-8.

[7] 黄传跃, 郭光海, 李祖钊. 一种新型旋翼/机身隔振装置及性能分析[J]. 振动工程学报, 1999, 12(3): 403-409.

HUANG Chuan-yue, GUO Guang-hai, LI Zu-zhao. A new rator/fuselage vibration isolator and its characteristic analysis[J].Journal of Vibration Engineering, 1999, 12(3): 403-409.

[8] 邓旭东, 刘勇. 橡胶弹性扭矩管式动力反共振隔振器性能分析[C]//第26届全国直升机年会学术论文集, 2010.

[9] Joseph T S. Helicopter gearbox isolation using periodically layered fluidic isolators [D]. United States：The Pennsylvania State University, 2003.

[10] Yilmaz C, Kikuchi N. Analysis and design of passive band-stop filter-type vibration isolation for low-frequency application [J]. Journal of Sound and Vibration, 2006, 291: 1004-1028.

[11] 王铁, 赵震, 陈峙,等. 某车架结构基于灵敏度分析的优化设计[J]. 机械科学与技术, 2013, 32(4):545-550.

WANG Tie, ZHAO Zhen, CHEN Zhi, et al. Optimization of the dump truck frame structure based on the sensitivity analysis [J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(4):545-550.

[12] 邬广铭, 史文库, 刘伟,等. 基于模态灵敏度分析的客车车身优化[J]. 振动与冲击, 2013, 32(3):41-45.

WU Guang-ming, SHI Wen-ku, LIU Wei,et al. Structural optimization of a light bus body-in-white based on modal sensitivity analysis[J]. Journal of Vibration and Shock, 2013, 32(3):41-45.

[13] 荣安琪. 重型卡车驾驶室模态灵敏度分析与结构优化[D]. 长春：吉林大学, 2009.

[14] 蒋荣超, 王登峰, 吕文超,等. 基于Kriging模型的驾驶室悬置系统多目标优化[J]. 农业机械学报,2015,46(3):344-350.

JIANG Rong-chao, WANG Deng-feng, LÜ Wen-chao,et al. Multi-objective optimization of cab suspension based on Kriging model[J]. Transactions of the Chinese Society for Agricultural Machinery,2015,46(3):344-350.

[15] 何成, 陈国平, 何欢. 基于全局近似函数的薄壁结构耐撞性多目标优化[J]. 南京航空航天大学学报, 2012, 44(4): 472-477.

HE Cheng, CHEN Guo-ping, HE Huan. Multi-objective optimazation of thin-walled structures crashworthiness based on global approxinate function[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2012, 44(4): 472-477.

Optimization design for dynamic anti-resonance isolators of helicopters’ rotor/fuselage

LI Yuanyuan, CHEN Guoping, WANG Ke

(The State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

To improve the isolation efficiency of helicopter rotor / fuselage anti-resonance isolator, optimization for the isolation system was conducted. The thickness of the front and rear flexible beams and their counterweight density were taken as the design variables through sensitivity analysis, and then the isolation efficiency and counterweight kinetic energy were optimized using genetic algorithms. Considering the lower computational efficiency problem due to simulation models directly calling the optimization algorithm, a surrogate model was established with the response surface method. The results showed that after optimization, a certain order anti-resonance frequency is consistent with the excitation frequency, counterweight vibration increases, force transmission rate decreases and vibration isolation efficiency is greatly improved; optimization design improves the dynamic isolators’ anti-resonance isolation performance and can provide a guidance for the design of helicopter vibration isolators.

helicopter; anti-resonance isolator; response surface; optimization

江苏高校优势学科建设工程资助项目；航空基金(20141552014)

2015-04-23修改稿收到日期：2015-07-11

李园园 女，博士生，1986年3月生

陈国平 男，博士，教授，博士生导师，1956年7月生

V223

A

10.13465/j.cnki.jvs.2016.15.019