不确定环境下项目型装配系统重调度研究

金腾飞，胡小锋，蒋 淳

(上海交通大学 机械与动力工程学院智能制造所，上海 200240)

0 引言

项目型产品通常为面向订单设计(Engineering to Order, ETO)的小批量产品，具有造价高昂、体积庞大、结构复杂、装配周期长的特点[1]。在项目型产品的装配过程中，常出现因物料供应不及时、零部件质量不合格、工人操作延时等不确定因素导致项目超期而给企业带来重大的经济损失。为此，在原计划受不确定因素干扰后，需及时实施重调度过程，以保持生产连续性、降低干扰造成的负面影响[2]。

近年来对于重调度的研究主要集中于单机系统[3]、Flow shop[4]以及Job Shop[5]领域。以上研究着重进行工作序列的重调度，生产扰动主要是新工作的插入，工作的执行时间都是固定的，没有考虑资源变动对于工作执行时间的影响。而目前为止仅有文献[6-7]进行了项目资源调度(RCPSP)类问题的重调度研究。在装配领域，Sabar等[8]研究了柔性装配线的人员排班重调度；Abd等[9]提出了田口模糊逻辑推理方法来解决机器人柔性装配重调度问题；Jung等[10]为双阶段装配流水车间调度问题建立了整数规划模型，并设计了三类不同编码方式的遗传算法进行求解。以上研究仅考虑了最小化完工时间这一目标，而项目型产品通常具有严格的交货期限，在交货期限内控制成本才是企业关心的重点。此外，上述关于重调度的文献大多没有考虑计划的稳定性，而工人配置的变化会带来额外的启动成本[11]。所以要求工人配置的调整尽可能小；工序开工时间的调整又会对物料配送、车间场地占用产生影响，因此，还要求工序开工时间的调整尽可能小。

根据上述分析，本文开展了针对项目型装配系统的重调度问题的研究，构建了以最小化项目成本和计划变动为目标的项目型装配系统重调度数学模型，并设计了一种基于帝国竞争[12]机制的双目标算法(MOICA)进行求解。模型和算法最终在汽轮机厂的阀门装配系统实例中得到了应用。

1 项目型装配重调度模型

1.1 问题描述

设某一项目型产品有JW道装配工序，工序不可拆分，工序间存在严格的先序约束关系，即不存在并行工序。企业一共分派W位工人执行该项目型产品的装配生产，每道工序一般由其中的若干位工人共同装配，装配同一个工序的工人称为一个装配组。工人的生产能力存在差异，工人具有不同的技能等级。在项目型装配系统中，工序的作业时间与工人配置，即装配组内工人数量与等级有关。增加工人或使用更高等级的工人能够缩短装配工序的作业时间，但同时意味着更多的成本投入。

1.2 条件假设

针对项目型装配系统有如下假设：

(1)车间内各类工装设备、零部件能满足制造要求；

(2)工序执行过程中装配组内的人员不发生变动；

(3)正常情况下工序一旦开始便不可中断，异常发生后，该工序的装配时间需重新计算；

(4)由于空间限制，同一时刻只能执行一道工序，即不存在并行工序；

(5)工序间存在严格的先序约束关系，所以重调度前后装配工序的顺序不发生变化；

(6)不同工人配置的装配组进行每一道工序装配的作业时间已知。

1.3 模型构建

1.3.1 参数定义

基本参数与变量定义如下：

(1)参数

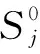
(2)决策变量

(1)

Sj∈[0,D),j=1,2,…,J

(2)

1.3.2 重调度模型

(3)

(4)

s.t.Sj≥Si+di∥Si≥Sj+dj,∀i≠j

(5)

(6)

Sj+dj≤D,∀j

(7)

(8)

dj=φ(x11,…,x1w,x21,…,xJ1,…,xJW)

(9)

xjw∈{0,1},∀j,∀w

(10)

式(3)、式(4)为模型目标，式(3)表示最小化项目成本，包含了工人工资成本和额外启动成本两部分，式(4)表示最小化重调度前后项目开工时间的总偏差；式(5)表示任一时刻只有一道工序在执行；式(6)表示不改变预调度计划下的工序执行顺序；式(7)表示工作要在项目交货期之前完成；式(8)表示各道工序的人员数量限制；式(9)表示工序作业时间dj是工人配置的函数；式(10)表示xjw为0～1变量。

2 基于帝国竞争机制的重调度算法

2.1 快速非支配排序方法

本文引入文献[13]中提出的快速非支配排序方法来计算各个解在解集中的非支配序，从而比较解的优劣，并形成Pareto解集。现设P为当前的解集，则对于P中的任意解p，首先计算如下两个指标：

np为集合P中支配p的解的数量；

Sp为p所支配的解的集合。

然后将所有np=0的解移出P并放入集合F1中，且F1中解的非支配序为1；此时对于F1中的每个解q，遍历Sq中的所有成员j并将其nj值减一；此时P中又会出现np=0的解，再将其放入集合F2中，且F2中解的非支配序为2。重复以上过程直到所有解的非支配序被确定。

2.2 算法主体

本文根据所研究对象的特点设计了一种基于帝国竞争机制的算法，算法流程如图1所示。

2.2.1 编码方式

本算法中个体编码的长度为参与重调度的工序数量J，式(11)所示为编码具体形式，其中每个点位cj称为基因片段，代表该道工序的工人配置情况，其与决策变量xjw(w=1,2…,W)的转换关系如式(12)。

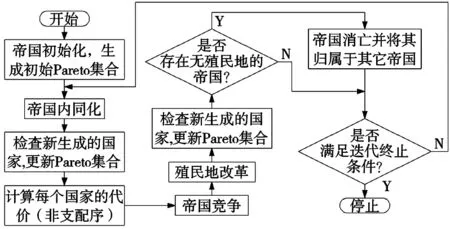
图1 算法流程

(11)

cj=2W-1xj1+2W-2xj2+…+20xjW

(12)

2.2.2 帝国初始化

帝国初始化的过程如下：

步骤1：根据公式(11)随机生成N个国家作为初始群体；

步骤2：根据解码规则计算各国的目标函数值(f1,f2)，使用快速非支配排序算法计算各国在群体中的非支配序，并将各国的代价函数值取为其非支配序。非支配序为1的解集中删除重复的解构成初始的Pareto集合。在竞争算法中，代价函数越小的国家势力越大。取势力较大的前Nimp个国家作为帝国，其余Nicol个国家作为殖民地，其中Nicol=N-Nimp。按照式(13)～式(15)计算每个帝国拥有的殖民地个数：

Cn=cn-1.3×max{ci}

(13)

(14)

NCn=round{pn×Nicol}

(15)

其中，cn是第n个帝国的代价函数值，Cn是标准化代价，pn是标准势力大小，round为取整函数，NCn表示第n个帝国的初始殖民地个数。

步骤3：从Ncol个殖民地中随机选择相应的个数分配给Nimp个帝国组成Nimp个帝国集团。

2.2.3 帝国内同化

步骤1：采用殖民地向帝国的移动来模拟帝国同化的机制，通过置换算子来实现移动的过程：即随机选取殖民地国家中半数基因片段，将其片段值置换为殖民地所属帝国相应基因片段上的值，移动过程如图2所示，灰色片段为随机选取的置换片段。

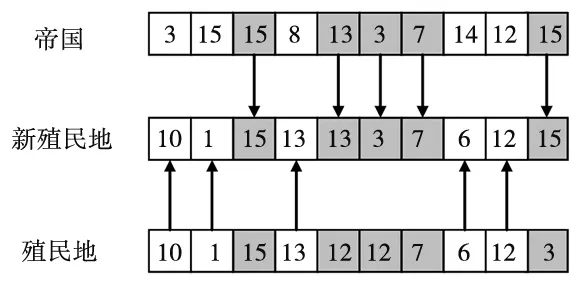
图2 帝国同化过程

步骤2：通过公式(16)来判断帝国与殖民地之间的相对势力大小，其中f1c与f2c分别为国家的两个目标函数值，Meanfk(k=1,2)分别为帝国集团内所有国家目标函数的均值。计算帝国集团内所有国家的γ值，若γ值最小的殖民地的γ值小于帝国的γ值，则交换帝国与该殖民地之间的位置。

(16)

2.2.4 帝国竞争及殖民地改革

帝国竞争过程如下：

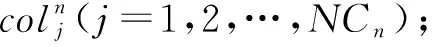
步骤2：根据式(17)计算各帝国的总代价函数值，函数值越小，帝国势力越大。式中μ为势力因子，一般取小于1的正实数；

(17)

步骤3：根据2.2.4中计算的γ值，取出各帝国集团中γ值最大的殖民地放入“自由国家”集合FC中；除去最弱帝国，将其余帝国放入“帝国集合”IC中；

步骤4：取出FC中代价函数值最大的国家，IC中帝国依据式(18)给出的概率计算公式占有该国家，并将得到新殖民地的帝国从IC中去除，重复该步骤直至IC=φ；

(18)

步骤5：重新将除最弱帝国外的帝国放入IC中，依据式(18)给出的公式将FC中最后一个国家分配给IC中的帝国。

为进一步提高全局搜索能力，在帝国竞争后增加殖民地改革操作：首先重新计算各帝国集团内国家的γ值，选取每个帝国集团中γ值最大的殖民地，然后以一个随机解来代替它。

2.2.5 帝国消亡

帝国竞争之后，帝国集团之间的势力差距会越来越大，最终会有帝国失去所有的殖民地而消亡。帝国消亡后，随机将其分配给其余帝国。

2.2.6 终止准则

满足如下3个条件之一即终止循环：①帝国集团的数量为1；②所有国家的非支配序为1；③循环次数达到限定值。

3 算法测试

3.1 实验数据

结合现场数据生成3类不同规模的数据，表1显示了3大类不同规模数据的工序数量、执行模式以及发生问题工序的组合情况。

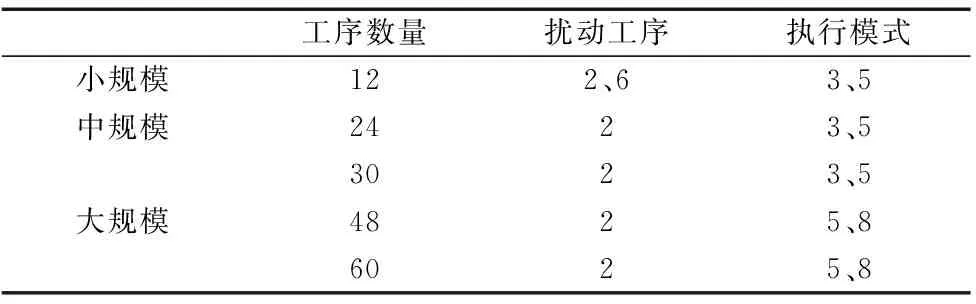
表1 实验数据归类

工序的启动成本和执行模式成本分别从区间(2，7)以及(20，100)中的均匀分布随机生成。生成工序时长时，首先从区间(20，200)中的均匀分布随机生成工序平均时长，设为T，则不同执行模式下的工序时长由区间(0.8×T,1.2×T)中的均匀分布随机生成，并与执行模式一一对应(执行成本越高的时长越短)。

生成延误时长时，首先计算案例的延误容许量，即未执行工序的最小作业时长总和减去初始计划中未执行工序的时长总和，则延误时间取为延误容许量的0.1、0.3以及0.5倍。

表2 初始数据

综上，首先为表1中的每种组合生成2组案例，每组案例均有三种不同的延误时间，所以共生成12×2×3 = 72个案例。其中小、中、大规模案例均为24个。

3.2 评价指标

3.2.1 最优覆盖率

小规模问题可在LINGO中求得最优解集，使用最优覆盖率对算法得到的解集进行评价。最优覆盖率(R)为一个算法所得解中Pareto最优解所占比例。式(19)中，P为算法得到的解集；Ppe为Pareto最优解集；|·|为解集中解的个数。

(19)

3.2.2 Hypervolume指标

在无法获得最优解集的中大规模问题上采用Hypervolume指标(IH)[14]对Pareto近似解集进行评价。

一般地，当归一化解集P={pi|1≤i≤n}，p0为参考点时，可按公式(20)计算IH(P)：

(20)

为使不同案例下得到的IH值进行比较，引入相对百分误差(relative percentage deviation, RPD)[1]作为方差分析的唯一因变量，如式(21)所示：

(21)

其中,Algsol表示单次算法运行得到的IH值，Maxsol表示得到的(当前案例)最大IH值。显然，RPD值越小代表结果越好。

3.3 算法性能测试

将本文的帝国竞争算法(ICA)与文献[13]中提出的快速非支配排序遗传算法(NSGA II)以及文献[14]中提出的加强Pareto进化算法(SPEA)进行了对比。测试数据为3.1节中生成的全部72个案例。

3.3.1 小规模案例测试

将24个小规模案例放入LINGO中进行求解得到了它们的精确解集。3个算法在扰动工序号为6的12个案例中均能求出最优解，表3显示了3个算法求解扰动工序号为2的12个案例得到的结果(以最优覆盖率显示)，可见本文提出的算法提供了最好的结果。

表3 小规模案例求解结果(最优覆盖率)

3.3.2 中大规模案例测试

中大规模案例无法在可承受时间内进行精确求解，我们使用解集的IH值来评价求解结果。同上一小节，为使不同案例下得到的IH值进行比较，计算单次运行结果的RPD值。表4所示为以初始工序数分组的求解RPD均值。进一步地，以算法为因子，RPD值为应变量进行方差分析以及LSD检验，图3所示为各个算法得到的RPD均值以及LSD误差范围，可见算法求解结果之间存在显著性差异，本文提出的帝国竞争算法能得到更好的结果。

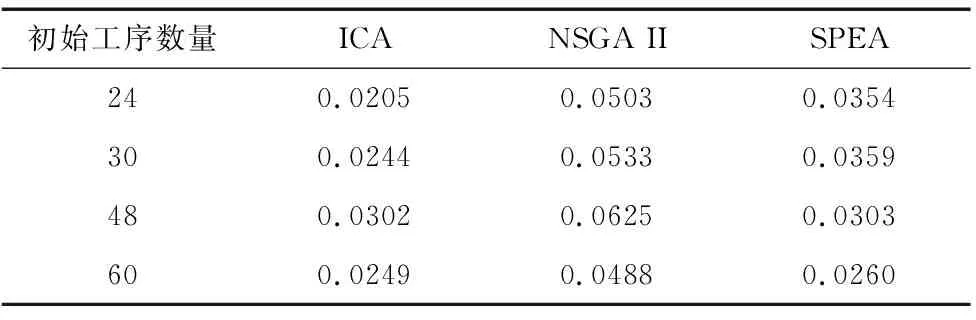
表4 中大规模案例求解结果(RPD均值)

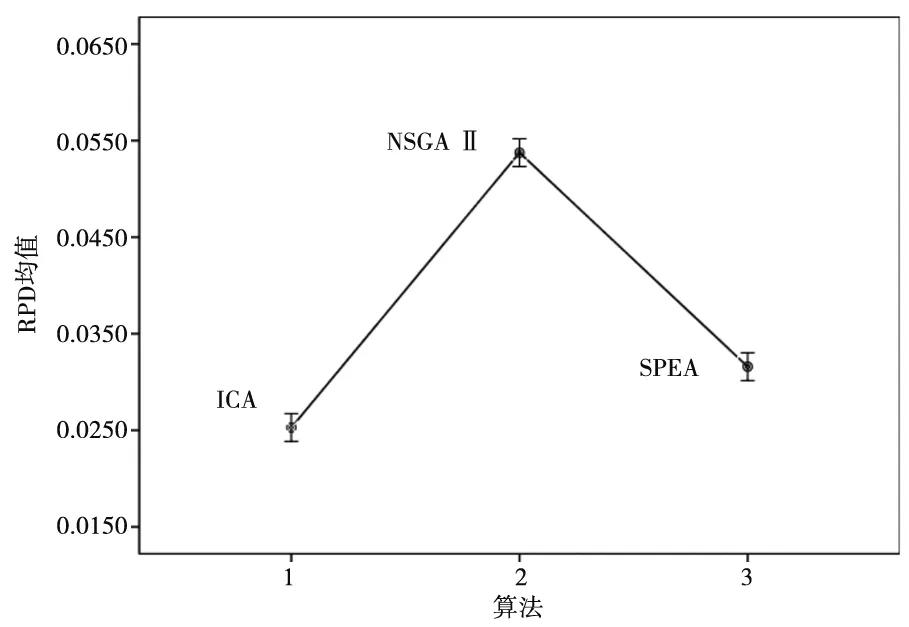
图3 不同算法得到的RPD均值及其LSD误差范围

4 工程案例

4.1 案例背景

本案例来源于某汽轮机阀门装配系统，该装配系统共包含24道装配工序，由阀门装配班组执行装配任务。阀门装配班组中共有两类不同技能等级的工人，其中有4名普工(A等级)，两名高工(B等级)。根据实际薪资水平，普工与高工单位时间的工人成本设置为1与1.3。实际生产时从装配班中选取若干人组成装配组执行装配工序，不同配置的工人组执行工序的时间不同。

4.2 扰动场景生成及求解

基于以上案例背景，现设有如下3种扰动事件：

(1)工序4处发生因零件返工问题导致项目有20单位时间的延误(J=20)；

(2)工序7因工艺更改造成工序时间翻倍(J=18)；

(3)工序9因液氮配送不及时造成35单位时间的延迟(J= 16)；

运行本文算法得到的Pareto近似解集，表5列出了Pareto近似解集在目标空间中的像，以(f1,f2)的形式表示，f1和f2分别表示项目成本和时间总偏差的值。

表5 Pareto近似解集对应的目标函数值

表6给出了事件目标函数为(1446,489)、(1484,108)、(1537,90) 的解重调度人员配置以及工序作业时长的变化情况(只列出了发生变化的工序，1A1B/33表示该道工序由1名A工人、2名B工人参与装配，工序时长为37)。图4为预调度计划以及以上3个重调度计划的甘特图，其工序方框内标有工序作业时长。

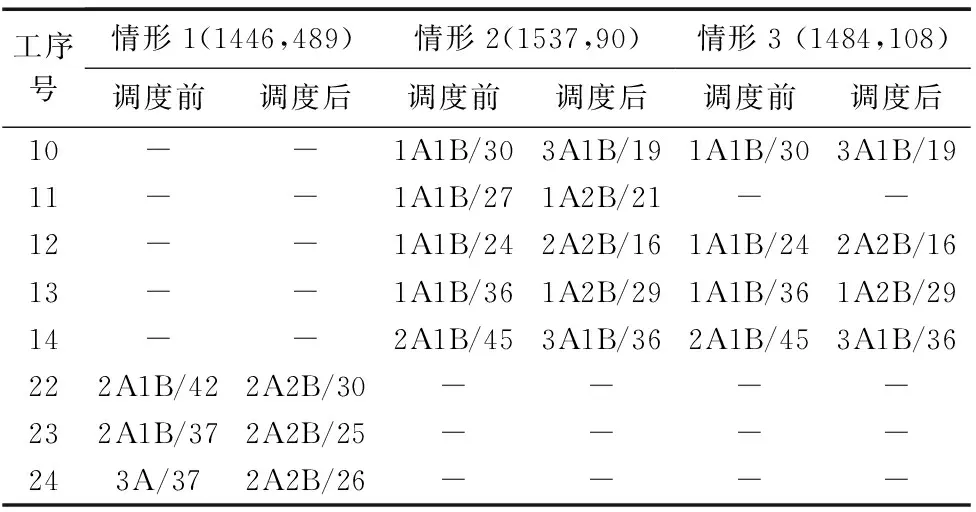
表6 重调度前后人员配置变化

定性分析模型中的两个目标，由于时间总偏差(目标2)总是在把资源投入越前置的工序时越小，而项目成本(目标1)则是在把资源投入边际成本与边际时间的比值越小的工序上达到越小的值。

结合表6以及图4给出的结果，情形2中前置工序投入了可支配的最大人力资源，其开工时间总偏差最小，但会导致高昂的项目成本；而情形1中项目成本最小，但若仅靠最后工序的资源重新配置来赶上项目交期，中间的大量工序开工时间都会延迟，会很大程度上扰乱车间的物流计划。在给出不同的重调度方案后，还需要根据现场的实际情况来确定最终的重调度方案。

图4 预调度计划及事件3中3种重调度计划的甘特图

5 结论

本文研究了不确定环境下的项目型装配系统中的工人重调度问题，构建了最小化成本和最小化重调度后计划较初始计划的偏离程度为目标的数学模型，并设计了多目标改进的帝国竞争算法进行求解，力求在优化目标的同时，保证项目按期交货。本文算法对帝国初始殖民地分配、同化以及消亡机制进行了优化，并增加了殖民地改革操作以增加算法的全局搜索能力。

算法测试结果显示本文算法在大小规模案例下均显著地优于NSGA II以及SPEA从而验证了本文提出的算法在求解本文模型时具有很好的性能。最后以汽轮机厂的阀门装配系统作为实例进行验证，得到了能有效执行的几个不同重调度方案，以供决策者选择。

虽然本文提出的模型和算法能够有效解决项目型装配的重调度问题，但该模型本质是针对单项目和无并行工位的装配系统的。在实际的项目型装配现场中，往往存在多项目同时执行(多阀门)以及存在并行工位的项目型装配系统(如汽缸装配)，因此，考虑多项目、并行工位将是后续研究的重点内容。