混合NSGA-Ⅱ算法求解多目标柔性作业车间调度问题*

景志强，王兆辉，高 琦

(山东大学 机械工程学院 CAD/CAM研究所，济南 250061)

0 引言

生产调度是影响制造业的重要因素，调度方法的研究与实施，对于企业提高生产效率、降低生产成本、节约能耗以及提高顾客满意度方面都起到了十分重要的作用。柔性作业车间调度(Flexible job scheduling problem，FJSP)是对传统作业车间调度问题的扩展，其中工件的某工序允许在多台机器中的某几台机器上加工，更加贴近实际。因而，柔性制造系统在当前的机械加工行业使用十分广泛。FJSP不仅需要确定工序加工的顺序，还要为每个工序分配机器，是一个复杂的NP-hard问题。

针对多目标优化问题，很多学者进行了研究。牛琳、刘燚[1-2]采用模拟退火算法融合遗传算法对调度领域进行了研究，获取优化调度策略。金敏[3]则是将遗传算法与粒子群算法相结合，提出了一种遗传算法和粒子群优化的多子群分层混合算法。张静[4]提出Baldwinian学习和模拟退火技术相结合的多目标局部搜索策略。张超勇[5]设计了一种改进的非支配排序遗传算法，改善原本算法在精英选择策略上的不足。鞠海华等[6-8]都是基于NSGA-II算法来对多目标调度问题进行求解。

从上述研究可以看出，单一算法由于搜索机制和进化方式，都会有各自的不足，因而采用混合算法求解将会改善寻优过程。目前的研究多为使用NSGA-II算法来求解，虽然其在多目标优化问题上体现了良好的求解能力，但在保持种群的多样性方面仍存在不足，为改善求解结果，引入模拟退火算法来执行选择过程，为子代提供更多的随机个体，增强整个算法的全局搜索能力。

1 FJSP调度模型

1.1 问题描述

柔性作业车间调度问题可描述为N个不同的工件在M台不同的机器上加工，每个工件有P道工序，且工序间的有先后约束。工件的每道工序可由M台机器上的一台或多台机器上加工，工件在各机器上的加工时间已知。确定N个工件在每台机器上的最优加工顺序，使得优化目标达到最优。

调度过程中要满足以下的约束条件：所有机器刚开始时均处空闲状态，在零时刻所有的工件都可进入生产系统进行加工；不同工件的工序之间没有先后约束，工件之间具备相同的优先级；工序的加工时间是确定的，某道工序完成后才能开始后道工序；工序一旦进行不能中断，同一时刻一台机器只能加工一道工序。

1.2 多目标优化模型

在车间调度的研究中常以最大完工时间、最大机器负荷、机器总负荷、加工质量、加工工期、加工成本、设备利用率、总拖期时间这些指标的组合作为多目标进行研究。

本文以最大完工时间、提前/拖期惩罚函数、生产总成本作为FJSP的多目标优化函数，对应的优化模型为：

(1)最大完工时间

调度的目标为确定每个工件的加工机器以及在加工开始和结束的时间，优化的方向为使得最大完工时间最小。其中ti表示工件i的完工时间，公式如下：

T=min(max(ti))

(1)

(2)提前/拖期惩罚函数

工件的加工应该满足交货期要求，而且也不应过早完成，造成库存浪费。最理想的结果是在各自的交货期时刻完成，因而要考虑提前/拖期惩罚函数，优化的方向为使得惩罚函数值最小。其中N为工件数量，M为机器数量，ri提前惩罚系数和wi拖期惩罚系数，di为工件的交货期，公式如下：

(2)

(3)成本函数

成本方面，本文只考虑机器加工过程中的成本。其中Xijk为工件i的工序j在机器k上的加工时间，Cijk为工件i的工序j在机器k上的单位成本。

(3)

2 混合NSGA-Ⅱ算法设计

2.1 基因编码

针对柔性作业车间调度的复杂性，本文采用双层编码原则。个体基因序列的前半部分代表工序的顺序，后半部分代表对应的加工机器。如3工件、每个工件3工序、6机器的调度问题的一个调度 [3 1 2 1 1 3 2 2 3 1 2 1 5 3 4 6 5 4]。

所代表的加工顺序为：工件3的第一道工序(加工机器为1)→工件1的第一道工序(加工机器为2)→工件2的第一道工序(加工机器为1)→工件1的第二道工序(加工机器为5)依次类推。

2.2 选择算子

本文采用模拟退火算法与模拟二进制选择相结合的方法对已进行非支配排序的个体进行选择。在原有模拟二进制的基础上，对于序值和拥挤距离这两个选择参数进行模拟退火操作，以实现全局搜索。操作步骤如下：

若RiRj，个体i的序值劣于个体j，按照Metropolis准则来进行操作，而且这个概率随着时间推移逐渐降低。倘若Ri=Rj则同理对拥挤距离进行模拟退火操作。模拟退火对应的概率公式为：

(4)

2.3 交叉与变异

交叉采用单点交叉的方式，变异采用线性的自适应变异来实现种群的进化，随着种群进化代数的不断增加，其变异概率会不断增大，加强算法的全局搜索能力。

2.4 算法流程

混合NSGA-Ⅱ算法是以遗传算法为基础(GA)，通过引入非支配排序、个体拥挤距离、精英保留与模拟退火的多目标优化算法。通过对种群中的个体进行非支配排序得到个体序值与拥挤距离，使用模拟退火与模拟二进制相结合的选择原则，进行选择操作。算法流程如图1所示。

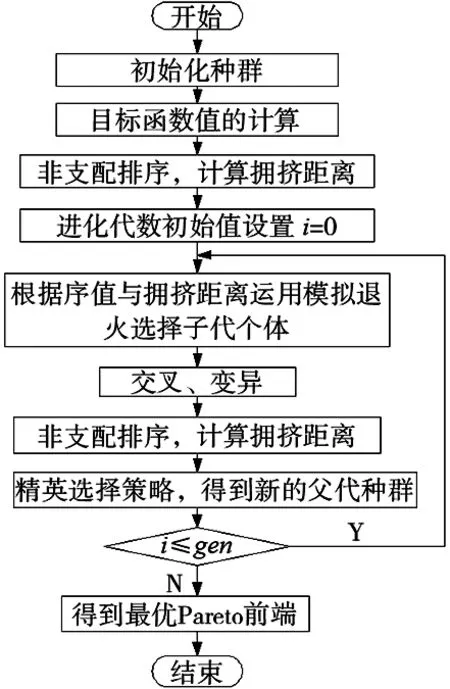
图1 混合NSGA-Ⅱ算法流程图

2.5 算法验证

本文将混合NSGA-Ⅱ算法与NSGA-Ⅱ算法进行了对比分析，针对的基准问题为一个双目标和一个三目标函数的优化，实验结果如下图，图中圆圈代表混合NSGA-Ⅱ算法的Pareto前端，星号代表NSGA-Ⅱ算法的Pareto前端。使用Matlab软件编程，得到结果如图2、图3所示，双目标优化结果对比见表1。

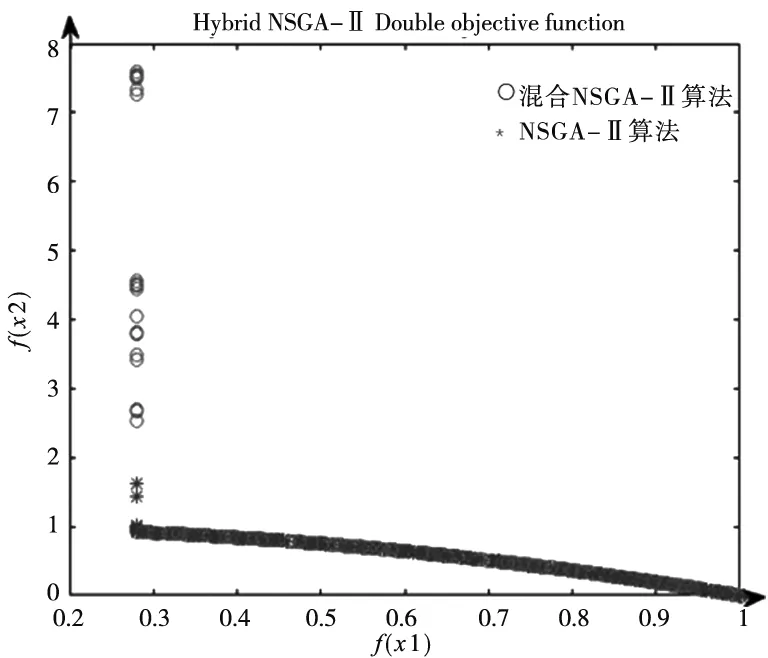
图2 混合NSGA-Ⅱ算法与NSGA-Ⅱ算法双目标求解结果对比图

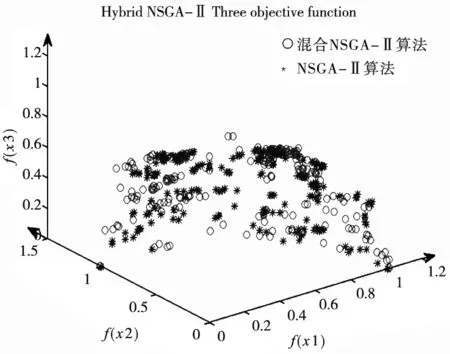
图3 混合NSGA-Ⅱ算法与NSGA-Ⅱ算法三目标求解结果对比图

双目标f(x1)f(x2)优化前(0.28,1)(0,1.7)优化后(0.28,1)(0,7.8)

可以明显看出混合NSGA-Ⅱ算法的Pareto前端的范围更广，说明其全局搜索能力更强。

3 车间调度仿真实例

本文参考文献6中的相关数据，对以最大完工时间、提前/拖期惩罚函数、生产总成本为优化目标车间调度问题进行验证。文献中的数据是针对6工件，每个工件有6个工序，10台机器的FJSP问题的研究。

本文新增了惩罚函数以及成本的相关参数，工序的可选机器号如表1所示，工序的加工时间如表3所示，工件惩罚函数相关参数如表4所示，各机床的单位时间成本如表5所示。

表2 各工序的可用机器

表3 各工序加工时间

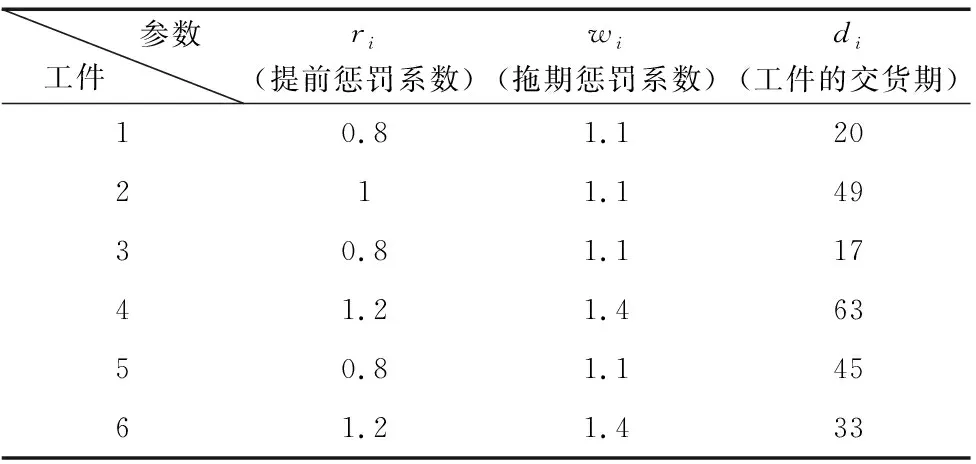
表4 各工件惩罚函数相关参数

表5 各机床的单位时间成本

得到如图4所示的Pareto前端，以及以如图5所示Pareto前端第一个解的甘特图。甘特图中的三位标号，第一位代表零件编号，后两位为零件工序号。如503，表示工件5的第3道工序。

针对完工时间、提前/拖期惩罚以及成本的三目标优化问题，求解得到了完整的Pareto前端，由图4可以明显看出，三个目标之间相互影响。在实际应用过程中，企业可根据实际情况选取合适的解，如注重减少成本则选取成本值较小的解。随后可以得到相应的甘特图，用于指导实际生产。

图4 混合NSGA-Ⅱ算法求解FJSP的Pareto前端

图5 柔性车间调度甘特图

4 总结

本文针对柔性作业车间调度问题，摒弃了将多目标转换为单目标的方式，使用改进的NSGA-Ⅱ算法，对多目标问题进行直接求解，并在求解过程中保持了解的多样性，得到车间调度的解决方案，为生产车间提供一系列可参考的调度，实现了最优调度方案的获取。

该研究为相关问题的解决提供新思路，可以进一步向流水车间调度问题或其他调度问题进行拓展。