真空管道列车动态运行气动特性研究

宋嘉源，李田，张继业

西南交通大学 牵引动力国家重点实验室，成都 610031

0 引言

真空管道运输系统（ETT）通过低真空与磁悬浮技术显著降低列车运行阻力，受到国内外研究人员的广泛关注。2005年，沈志云院士[1]提出并论证了中国发展600km/h真空管道高速交通的设想。2013年，Musk[2]提出了Hyperloop 真空管道胶囊车的概念。2020年5月，西南交通大学启动了“多态耦合轨道交通动模试验平台”项目，计划建设超导磁浮技术与低真空技术结合的综合性试验平台。与目前的高速列车[3]相比，真空管道列车高速运行时流场中存在一系列复杂的气动现象[4]，如前驱激波、尾部激波、壅塞流动等。

数值计算是研究真空管道列车的主要方法之一。Niu 等[5-6]采用轴对称的简化模型作为研究对象，利用数值计算模拟了不同运行速度和阻塞比的真空管道列车气动及气动热特性，拟合了压力系数与列车运行速度的关系。Kim[7]、Choi[8]和Zhou[9]等研究了真空管道列车的气动阻力与阻塞比、真空度及列车运行速度的关系。针对二维管道内复杂的激波现象，周鹏等[10-11]采用自适应网格技术精确捕捉激波位置，研究了1 250 km/h 二维管道列车激波的产生与反射传播规律。三维磁浮列车需要考虑悬浮间隙和非轴对称的几何外形，管道内会出现更复杂的激波及气动热现象[12]。胡啸等[13-14]采用IDDES 方法研究了三维磁浮列车的热压载荷分布及其瞬态特性，得到了热压载荷的频率和分布规律。此外，为减少数值模拟计算的时间，Hou 等[15]指出准一维的管道列车模型和数值方法适用于真空管道流场研究，并推导了基于无黏与黏性气体的典型流动模型和流型之间的过渡极限，其中等熵极限与激波脱离极限分别对应于壅塞流动和激波脱离现象。张晓涵等[16]结合进气道理论与数值仿真阐明了管道气流壅塞现象的形成机理。Li 等[17]采用一维流动理论快速预测了管道列车周围的气流参数。

目前多数学者的研究主要针对匀速运行的管道列车，对列车加/减速运行时的气动阻力及特性的关注较少[18]。本文建立三维列车计算模型，采用剪切应力输运（Shear Stress Transport,SST）k–ω模型求解管道内的流场，通过对比匀速工况和不同加速度工况的列车气动阻力时程曲线以及不同时刻管道内的压力分布，揭示加速度对列车气动阻力和管道流场特性的影响规律，为真空管道试验平台的建设提供一定参考。

1 数值模型

1.1 控制方程

真空管道列车高速运行时的马赫数大于0.3，会引起一系列复杂的气动现象（如前驱激波、壅塞流动和尾部激波），因此数值模拟需要考虑空气的可压缩性。根据气体连续性假设、动量守恒和能量守恒关系得到连续性方程、动量方程和能量方程[19]：

式中：ρ为气体密度；t 为时间；xi、xj为直角坐标分量，ui、uj分别为流体速度u 在xi、xj上的分量；p 为压力；τij为黏性应力张量；e 为内能；h 为焓；K 为热传导系数；T 为温度；i、j 取1、2、3 分别代表 x、y、z方向。

管道内空气剧烈压缩和膨胀会引起较大的温度变化，造成不同区域气体黏度不同，采用Sutherland公式可以更准确地描述气体温度与黏度的关系[20]：

式中：µ为气体动力黏度；µ0= 1.71 × 10−5Pa·s，为标准气压环境（101 325 Pa、273.15 K）下的气体动力黏度；T0为温度参考值，取273.15 K；S 为Sutherland常数，取110.4 K。

1.2 等熵极限与激波脱离极限

根据一维等熵流动理论，当来流马赫数超过临界值时，列车周围气流可通过的最大质量流量受到限制，气流发生壅塞并产生前驱激波。壅塞现象对应的来流马赫数Ma 为等熵极限的临界速度[16]：

式中：阻塞比β=Strain/Stube，其中Strain为列车在运行方向（x 方向）的投影面积，Stube为管道在列车运行方向的投影面积；γ为空气绝热指数，取1.4。

当列车运行速度不低于等熵极限的临界速度时，列车前方与尾部分别产生前驱激波和尾部激波。在管道参考系下，当列车速度继续增大至大于尾部激波速度，尾部激波发生脱离并向列车后方传播。根据一维流动理论[3]可以确定尾部激波脱离极限的临界速度，如图1所示。

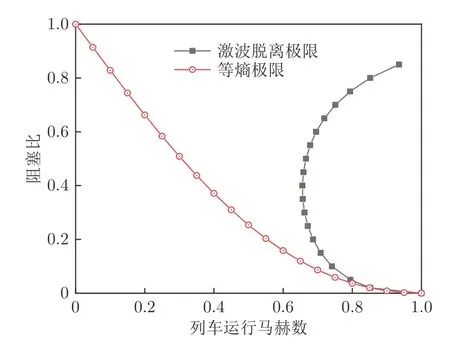
图1 等熵极限与激波脱离极限Fig.1 Isentropic limit and shock detachment limit

1.3 计算工况

为模拟列车速度达到不同极限（等熵极限和激波脱离极限）时的气动现象，并对比不同加速度对气动阻力及流场的影响，设置了3 种不同的计算工况。图2 为不同工况下列车的运行速度及距离。工况1、2 的加速度a 分别为385 和278 m/s2，当列车加速至333 m/s 时，停止加速并保持匀速行驶；工况3 列车一直保持333 m/s 匀速运动。

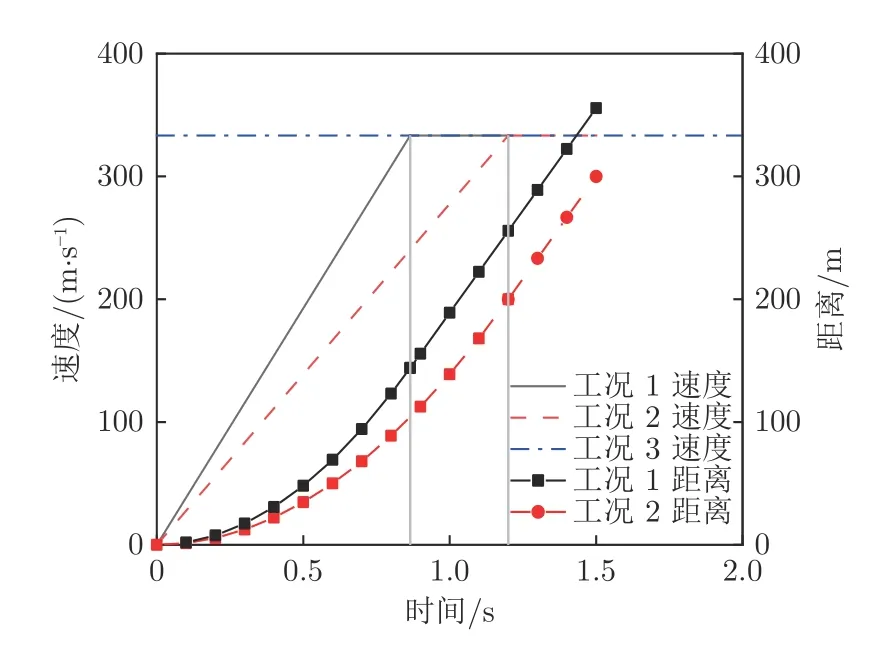
图2 不同计算工况的速度和距离时程曲线Fig.2 Curve of speed and distance under different cases

2 数值模拟方法

2.1 几何模型

如图3所示，采用三维真空管道列车模型进行数值模拟。为保证头尾车流线型的细长比与高速磁浮列车接近，设置列车中心截面的轮廓曲线为列车采用3 编组结构，总车长度Lt为40 m，头、尾车长度都为10 m，中间车长度为20 m，直径D 为3.5 m。管道总长为550 m，在运动初始位置，列车头车鼻尖距离隧道入口400 m。管道直径为11.07 m，不同工况下列车的阻塞比均为0.1。

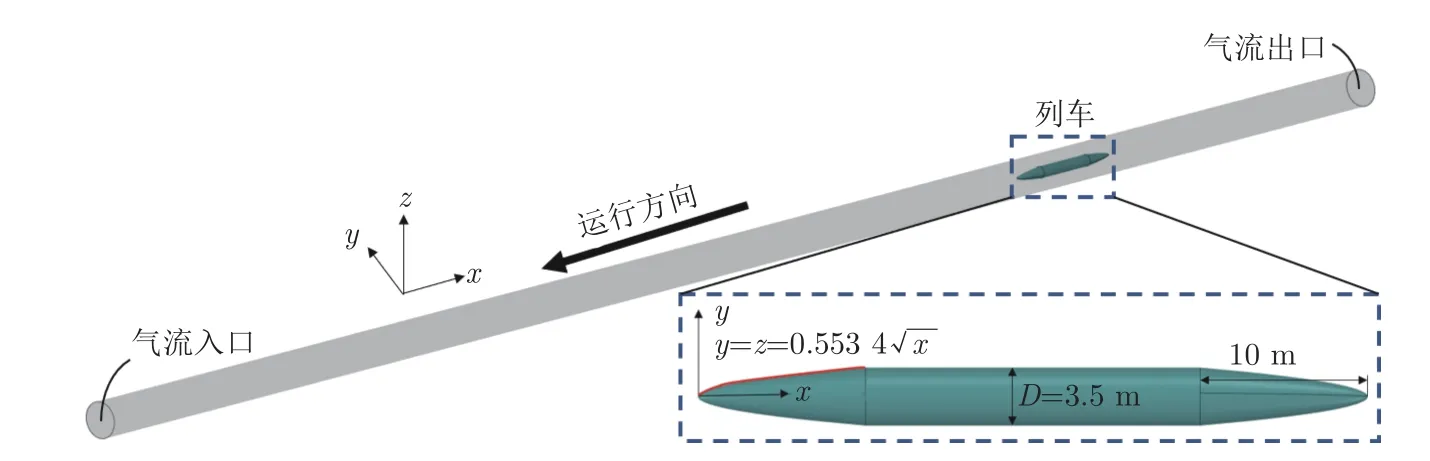
图3 几何模型Fig.3 Geometric model

2.2 计算域与边界条件

图4 为模型计算域与边界条件，环境压力设为20 265 Pa，温度设为288.15 K。为保证出入口边界不影响管道内流场分布，设置出入口边界为压力出口，相对压力为0，管道壁面设置为固定绝热壁面。采用重叠网格技术模拟列车运行过程，计算域分为重叠区域与背景区域，重叠区域直径为4.7 m，重叠区域前、后边界与头、尾车距离分别为10 和30 m。

图4 计算域与边界条件Fig.4 Calculation domain and boundary conditions

2.3 计算模型

根据流体控制方程建立了三维可压的数值计算模型，雷诺平均方法被广泛应用于高速列车与真空管道列车数值模拟中[5]，本文采用了SST k–ω湍流模型。采用隐式非稳态耦合流算法求解控制方程，时间离散项为二阶。计算的时间步长为1 × 10−4s，内部迭代步数为20。初始压力和温度分别为20 265 Pa和288.15 K，参考压力与环境压力相同。

2.4 网格划分方法

由于真空管道列车运动计算域较大，为提高计算效率，采用重叠网格技术模拟列车运动过程。重叠网格技术通过重叠区域网格单元与背景区域网格单元的数据交换进行耦合，可以有效降低总网格数量。设置重叠区域与背景区域的网格单元尺寸一致可以降低计算误差。此外，重叠网格的收敛速率与相同分辨率的单个网格相同。

划分了如图5所示的重叠网格及背景网格用于数值计算，为保证2 套网格过渡良好，背景网格的基础尺寸设置为200 mm，重叠区域添加了2 个加密区，基础尺寸分别为50 和100 mm，重叠网格最外层尺寸为200 mm。真空管道列车尾部流场更加复杂，为更好地捕捉尾部激波及后方尾流，设置尾车鼻尖与重叠网格交界面后侧的距离为30 m。如图5 右上框所示，列车近壁面划分了总厚度为10 mm 的15 层边界层网格，列车表面网格的基础尺寸为50 mm。

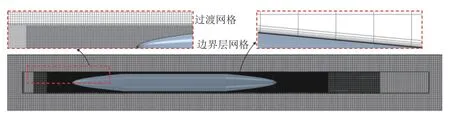
图5 计算域网格划分Fig.5 Mesh of computational domain

2.5 激波管验证

1955年，Trimpi 和Cohen[21]提出了预测激波管内气流流动的理论公式，并与激波管试验数据进行了对比。图6 为该试验的装置示意图，激波管左侧为高压段，右侧为低压段，交界面处有1 或2 片0.003 175或0.003 81 cm 的软黄铜垫片作为膜片，将高低压段隔开。初始状态下，低压段气体压力等于环境压力（101 325 Pa），高压段气体压力分别为45、70 和95 psi（即411 481、584 037 和755 378 Pa），气体温度均为室温300 K。该试验开始时，通过装置戳破薄膜，交界面处将产生激波向低压段传播并衰减，在距膜片3.23、5.23、7.23、9.18 和11.18 英尺（即0.984 5、1.594 1、2.203 7、2.798 和3.407 7 m）处监测压力，得到激波通过前后压力比与膜片距离的关系。在数值模拟时使用了SST k–ω湍流模型进行求解，考虑气体传热，求解精度为隐式二阶。时间步长设为10−6s，最大迭代次数为20 次。

图6 激波管装置示意图[21]Fig.6 Schematic diagram of shock tube[21]

图7 为0.001 s 时刻激波管内的压力分布和波系结构。图8 为激波通过前后压力比的试验和数值模拟结果对比，高压段压力为45、70 和95 psi 条件下对应最大误差分别为1.08%，1.16%和1.38%。结果表明，当前模型能准确捕捉激波管内激波的瞬态传播特征。

图7 0.001 s 时刻激波管内压力分布Fig.7 Pressure distribution in shock tube at 0.001 s

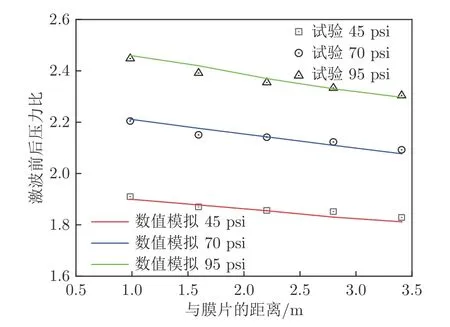
图8 Trimpi 实验[21]与数值计算结果对比Fig.8 Comparison of Trimpi experiment and simulation[21]

3 数值模拟结果分析

3.1 气动阻力瞬态特性分析

根据1.2 小节关于等熵极限与激波脱离极限的讨论，在管道列车阻塞比为0.1 时，壅塞极限与激波脱离极限对应的临界马赫数分别为0.678 和0.741，在工况2 中对应的时刻分别为0.83 和0.91 s。图9为工况2 头、尾车气动阻力的时程曲线，呈现先增加后稳定的趋势；在0～0.5 s，管道内流场处于非壅塞状态，尾车阻力增长缓慢，而头车阻力随列车加速基本不变。图10 和11 分别为列车周围压力分布和列车表面压力分布情况。0～0.1 s，列车启动形成了流场初始扰动，正压主要集中在头车周围；0.1～0.4 s，气流在头车鼻尖位置被剧烈压缩产生正压聚集区域，经过鼻尖时压力快速降低；当气流通过头车周围的流通区域时，头车表面压力由正变负，负压在头车与中间车连接处达到最大值。0.1～0.4 s，头车阻力受到正负压区域共同影响，正负压力同时增大，因此阻力变化不明显，而尾车阻力随表面负压增大逐渐增大。如图11所示，在0.1、0.3 和0.5 s 时刻，头车鼻尖的最大正压分别为2.756、1.071 和0.214 kPa，与运行距离基本呈线性关系。列车匀加速过程中运行距离x ∝t2，因此列车表面最大压力pmax∝t2。

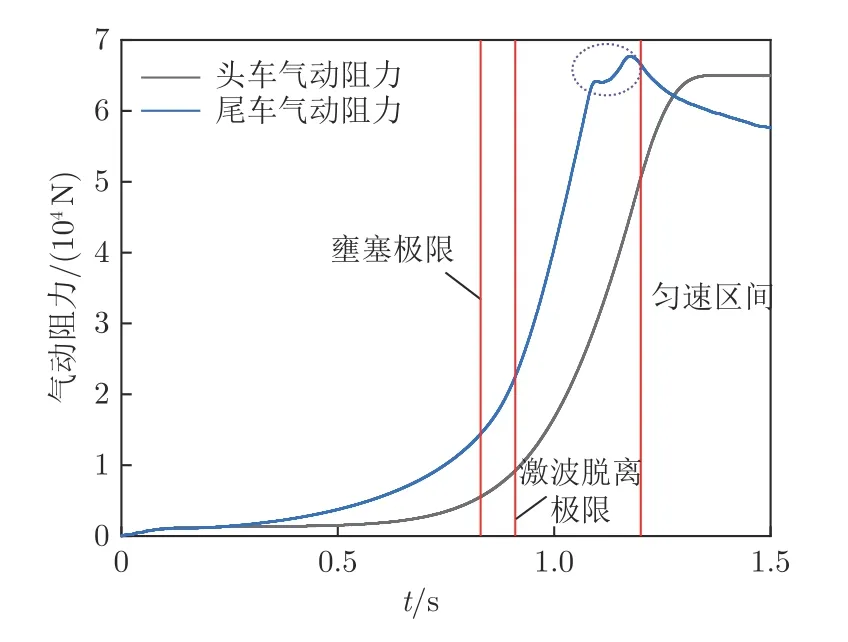
图9 工况2 气动阻力时程曲线Fig.9 Curve of aerodynamic resistance under case 2

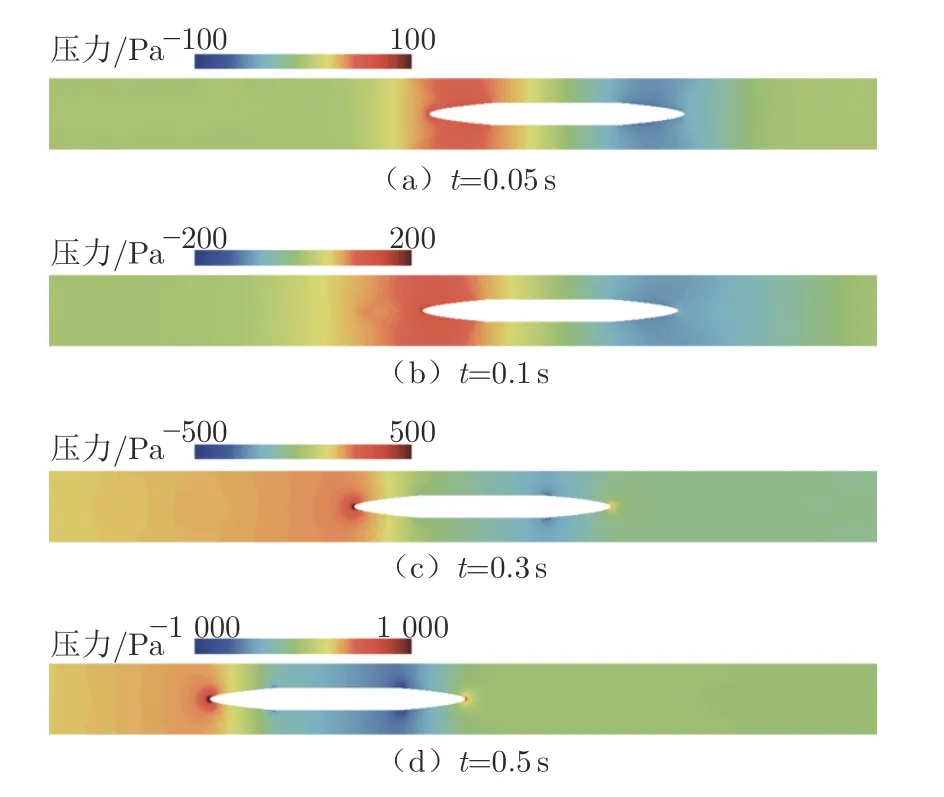
图10 工况2 下0～0.5 s 列车周围压力分布Fig.10 Pressure distribution around the train under case 2 of 0～0.5 s

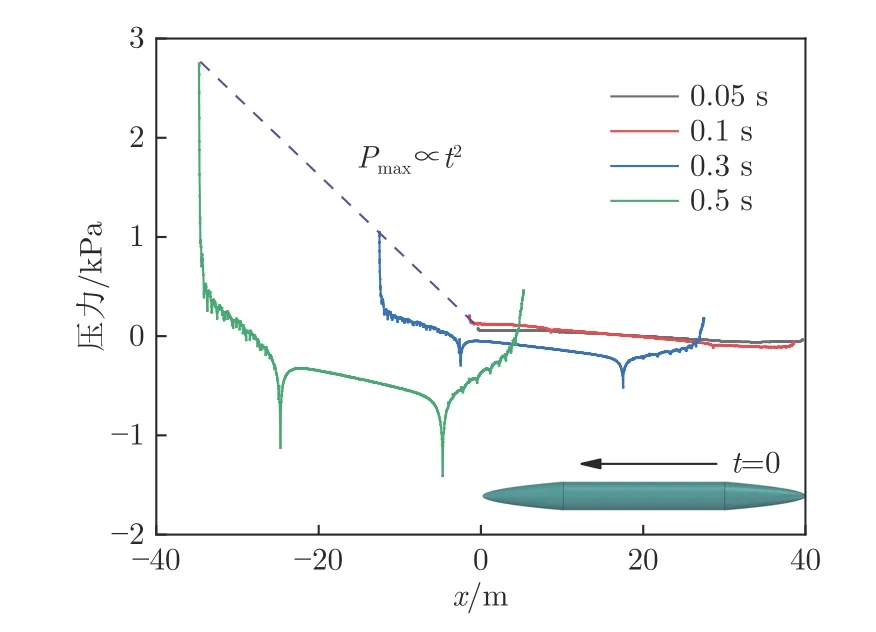
图11 工况2 不同时刻列车表面压力分布Fig.11 Pressure distribution of surface at different times under case 2

图12 为t=0.6～1.2 s 列车周围压力分布。t=0.83 s 时刻，真空管道列车达到壅塞极限，通过列车周围流通区域的空气质量流量受到限制，列车前方的壅塞现象造成头尾车气动阻力增长速度明显变快。同时，气流在中间车与尾车连接处膨胀加速，横截面积的突变导致该位置产生膨胀波，随着气流继续加速，在尾车流线型膨胀过度并产生尾部激波。t=0.91 s 时刻，真空管道列车达到激波脱离极限，随着列车继续加速，尾部激波和膨胀波相对于列车向后运动，波系在管道与列车表面之间反射传播。当膨胀波反射并击中尾车表面时，尾车气动阻力产生波动，如图9所示。t>1.2 s 时，列车保持速度为1 200 km/h 的匀速运动，壅塞气流聚集产生的前驱激波会继续向前方流场传播，但对头车周围流场影响较小。由于尾部激波和膨胀波不断向后传播，尾车周围流场继续变化，尾车阻力缓慢减小并逐渐趋于稳定。

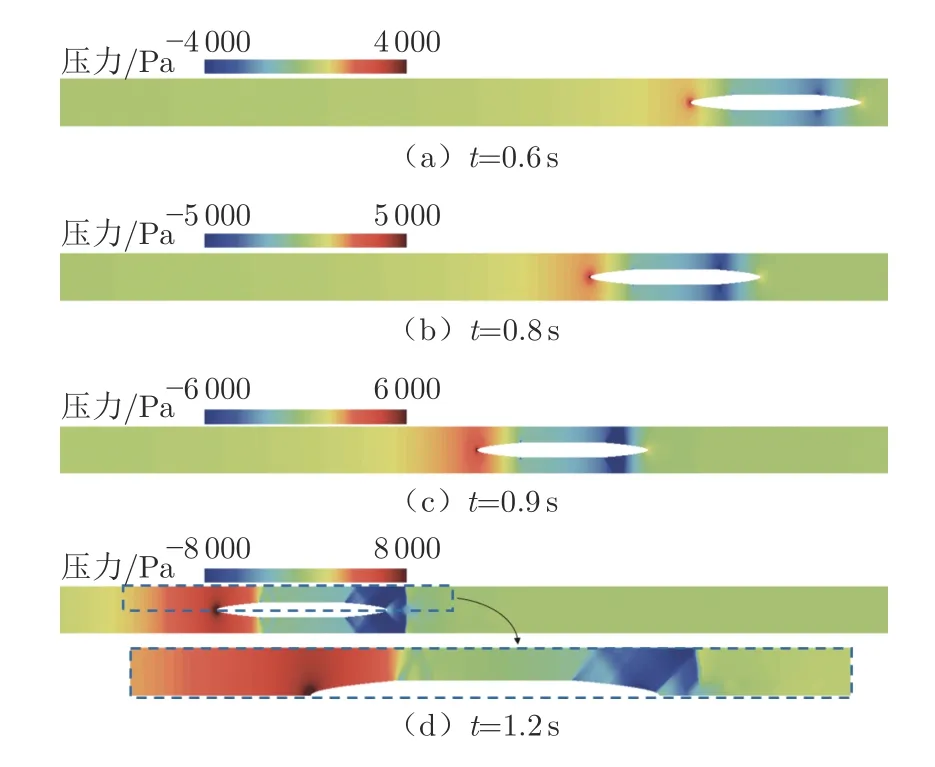
图12 工况2 下0.6～1.2 s 列车周围压力分布Fig.12 Pressure distribution around the train under case 2 of 0.6～1.2 s

图13 为管道内流场稳定即t=1.5 s 时刻管道内的速度矢量图。由于前驱激波在管道参考系下的运行速度大于列车，随运行时间增加，未受扰动的流场区域相对于头车越来越远。在头车与中间车连接处，壅塞现象限制了气流流动，如图13 的局部放大图所示，头车带动的一部分气流没有通过流通区域进入后方流场，而是堆积在列车前方区域，导致壅塞段变长。尾部流场的分布具有周期特性，尾部激波在管道壁面间反射，并在后方流场形成了多个马赫杆。气流通过间断面[4]时速度发生突变，间断面后的流场速度基本为0，但列车尾流的影响距离较远，并在尾流两侧形成强度较低的涡旋。

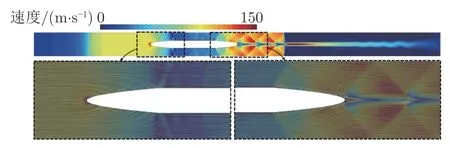
图13 工况2 下1.5 s 时刻管道内速度矢量图Fig.13 Velocity vector diagram in the tube under case 2 at 1.5 s

3.2 加速工况与匀速工况对比

图14 为工况3 头、尾车气动阻力的时程曲线。由图9 和14 可知，当流场基本稳定时，工况2 和3 的头车气动阻力分别为64 929 和64 448 N，偏差为0.74%，尾车气动阻力分别为57 778 和56 027 N，偏差为3.13%，因此，加速阶段基本不影响流场稳定时的气动阻力。与工况2 相比，在工况3 的初期阶段（t=0～0.2 s），头车气动阻力的增长速率基本不变，而尾车气动阻力发生了周期性波动，振荡幅值随运行时间增长不断衰减，在t=0.09 和0.11 s 时刻，尾车气动阻力明显降低。

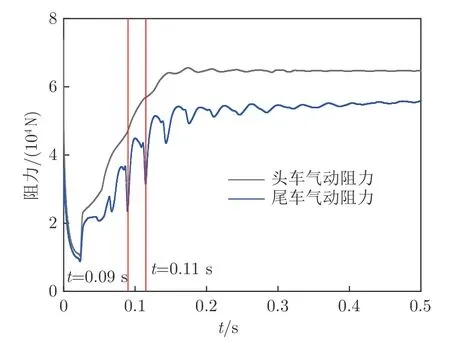
图14 工况3 列车气动阻力时程曲线Fig.14 Curve of aerodynamic resistance under case 3

为分析工况3 尾车气动阻力大幅波动的原因，提取了t=0.09、0.1 和0.11 s 3 个时刻列车表面压力分布曲线，如图15所示。可以看出气流通过头尾车时压力的变化趋势和幅值基本相同，列车表面压力分布差异主要集中在中间车。不同时刻中间车与尾车连接处的压力不同，从而影响了尾车整体的压力分布。

图15 工况3 不同时刻列车表面压力Fig.15 Pressure distribution of surface at different times under case 3

图16 为工况3 下不同时刻列车周围压力分布，t=0.09 s 时刻，头车前方的壅塞气流通过头车与中间车连接处时产生斜激波，随着时间增加，斜激波的角度逐渐变大，在管道壁面和列车表面的反射点位置发生移动，造成中间车表面压力变化较大。当反射点位于中间车与尾车的连接处时，反射点附近的正压区域会影响尾车表面压力分布，使其出现周期性的压力波动，从而影响尾车气动阻力。随着反射次数的增加，斜激波强度逐渐变小，尾车气动阻力的振荡幅值逐渐降低。

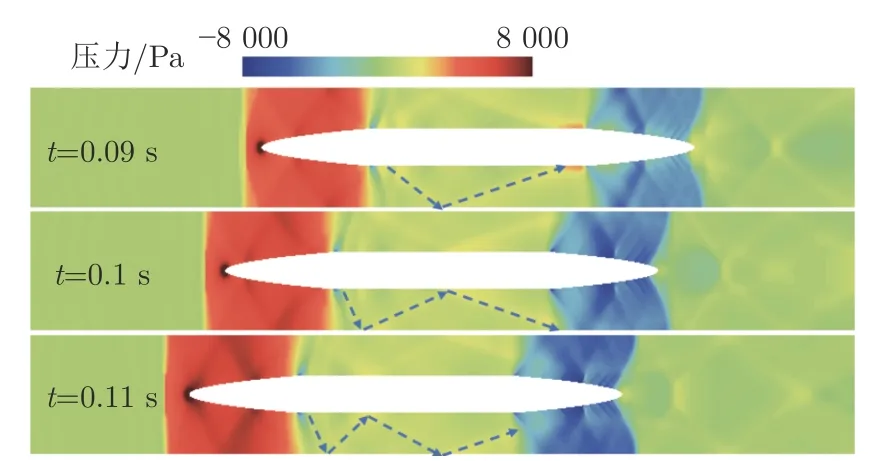
图16 工况3 不同时刻列车周围压力分布Fig.16 Pressure distribution around the train at different times under case 3

3.3 不同加速工况对比

图17～19 分别为工况3、2、1 不同时刻的管道压力分布。在匀速工况下，头尾车周围压力与运行距离基本呈线性关系，并在大约t=0.16 s 时刻头尾车周围压力基本同时达到最值。在工况1 和2 下，尾车周围压力首先达到最小值，在加速阶段完成后列车匀速运行，头车周围压力继续保持一段时间增长，在大约t=1.4 s（工况2）和t=1 s 时刻（工况1）达到最大值。这是由于在加速阶段完成时刻，加速工况下头车压缩前方空气过程较缓慢，对应的压力梯度较小，前驱激波强度小于工况3，头车将继续压缩前方空气直到前驱激波后的气流压力和马赫数稳定。总体看来，头车气动阻力和周围压力变化与运行速度变化相比表现出一定的滞后性，且加速度越小，滞后性越明显。

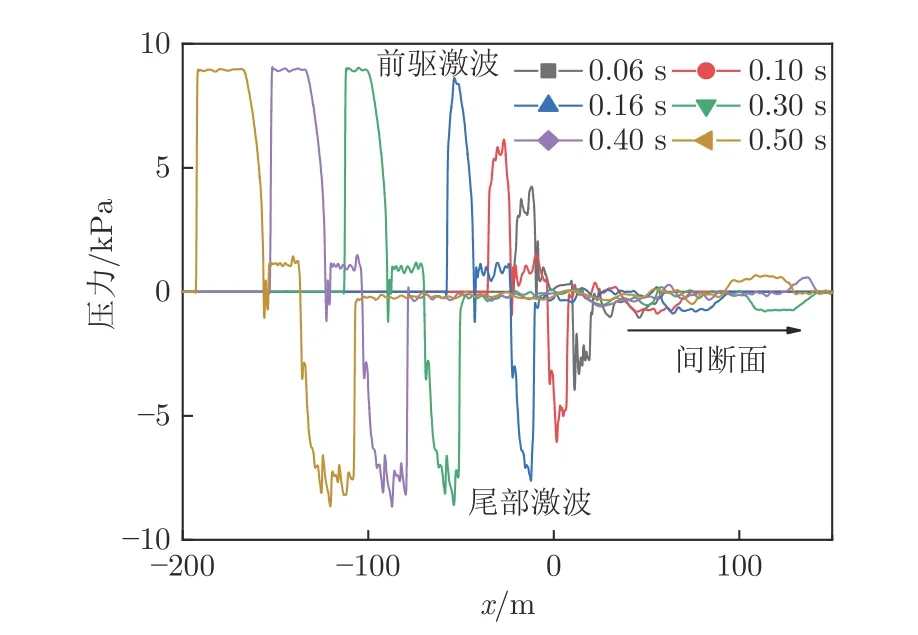
图17 工况3 不同时刻管道内压力分布Fig.17 Pressure distribution in tube at different times under case 3

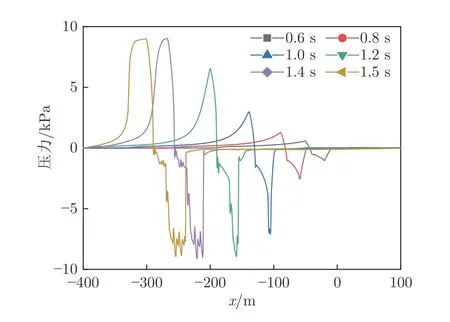
图18 工况2 不同时刻管道内压力分布Fig.18 Pressure distribution in tube at different times under case 2

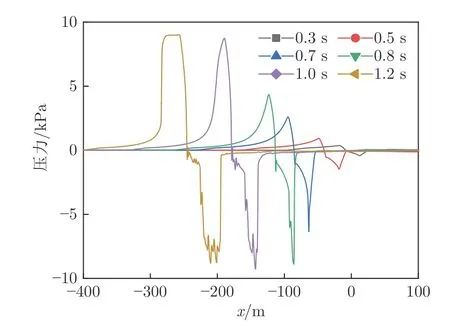
图19 工况1 不同时刻管道内压力分布Fig.19 Pressure distribution in tube at different times under case 1

在头尾车周围压力达到最值后，随着列车匀速运动，前驱激波与头车鼻尖间的壅塞段长度增加，尾部激波向后方流场的传播距离也增加。以工况3 为例，当t=0.3、0.4 和0.5 s 时，壅塞段长度分别为12、18 和24 m，尾部激波段长度分别为11、16 和20 m，与运行时间成正比。对于尾部流场，匀速工况列车启动速度较大，形成尾部激波、中心间断面和尾部膨胀波等一系列气动现象，气流经过激波及膨胀波时压力先降低后恢复。在加速度阶段，由于启动速度较低，尾部压力波动不明显。

4 结论

本文建立了三维真空管道列车模型，采用SST k–ω模型求解了管道内的流场，研究了匀速工况和两个不同加速度工况下的瞬态列车气动阻力、流场特性以及管道压力分布，主要得到以下结论：

1）管道在非壅塞状态下，尾车气动阻力增长缓慢，头车气动阻力基本不变；达到壅塞状态后，头尾车气动阻力快速增大；达到激波脱离极限和加速阶段完成后，尾车与头车气动阻力都趋于稳定。

2）流场稳定时加速工况与匀速工况的气动阻力相对误差较小，由于匀速工况启动速度较大，头车与中间车连接处产生的斜激波影响列车表面压力，导致尾车阻力大幅波动，波动幅值随运行时间增长逐渐降低。此外，在匀速工况下，尾部流场还存在中心间断面和尾部膨胀波等一系列气动现象。

3）由于加速工况下头车压缩前方空气过程较缓慢，前驱激波强度较低，头车气动阻力和周围压力的变化与运行速度变化相比表现出一定滞后性，并且加速度越小滞后性越明显。

4）在加速阶段，尾车周围压力比头车先达到最值，匀速阶段头尾车周围压力基本不变；壅塞段长度和尾部激波段长度与列车运行时间成正比关系。