基于改进FPM法高维复杂多相分离过程的GPU并行计算研究*

甄玉洁，胥 康，蒋 涛，任金莲

（扬州大学 数学科学学院，江苏 扬州 225002）

引言

含高阶导数的多元Cahn-Hilliard (C-H)方程常被用来描述多相流体力学或热力学等领域中的复杂非线性相分离现象[1-4].近些年来，多元C-H 的高效性数值模拟方法研究受到许多国际学者的关注，目前，已有多种基于网格类方法被成功地用于单变量C-H 方程下非线性扩散或高维多元C-H 方程下相分离过程的数值预测，如有限元法[5]、有限差分法[6-8]和多重网格法等[9-10].上述方法对多元C-H 描述的多维复杂非规则相界面的模拟实现比较复杂，且不易实施多CPU 或异构图形处理器(GPU)的并行计算.于是，近年来不完全依赖网格的纯无网格法在国际科学计算领域中受到普遍关注.相较于网格类方法，无网格方法[11-15]具有易推广到复杂区域问题求解和高维问题并行计算实施的优点[15-20]，如有限点集法(finite pointset method,FPM)[21-24]和光滑粒子流体动力学(简称SPH)法等[15,20-23].

然而，上述纯无网格FPM 和SPH 法推广应用到C-H 方程下多相分离过程的模拟在国际上还鲜有报道.笔者在2020年首次将FPM 拓展到二维单分量C-H 方程的求解，并发展了基于局部加密的LR-FPM 法(见文献[24])，将其直接推广应用到多元C-H 方程下三维复杂多相分离过程的模拟涉及巨大计算耗时问题，且计算精度有待进一步提高.FPM 数值模拟多元C-H 下三维多相分离过程较网格类方法的主要优点在于：① 易处理高维复杂相界面和易离散求解四阶空间导数；② 易并行计算实施.

基于上述分析，拓展FPM，采用Wendland 权函数，引入基于CUDA 的CPU-GPU 异构并行计算，提出了一种能够高效、准确地模拟多元C-H 方程下高维复杂多相界面分离过程的改进FPM GPU 并行算法(CFPMGPU).首先采用Wendland 权函数的FPM 对四阶导数分裂成的两个二阶空间导数依次离散；其次准确施加Neumann 边界条件；最后，采用基于CUDA 语言的单个CPU-GPU 异构协同的并行计算方式给出上述离散过程的GPU并行算法以加速计算模拟.本文并行计算模拟中采用一个型号为TITAN RTX 的GPU，其包含24 GB显存和4608 个CUDA 核心数.数值算例中首先展现了方法的准确性和并行计算效果；其次对二维复杂二或三相分离过程，以及三维复杂二相分离过程进行了模拟预测.

1 三元C-H 方程

本文主要研究多元C-H 描述的相分离现象[1,10]，考虑如下三元C-H 方程在区域Ω ⊂Rd(维数d=2 或3)内的形式：

在边界 ∂Ω上满足齐次Neumann 边界条件

其中，ϕi(x,t)(i=1,2,3)为三元混合物中每个分量的摩尔数，n为边界上的单位法向量.根据质量守恒律，摩尔数总和须满足

在本文数值模拟中，利用ϕ3表示一个任意复杂区域(相分离现象发生在区域内)，区域上ϕ3≈0，其余区域，在区域边界上考虑ϕ3≈0.5(可详见文献[10]).此外，根据式(3)可得.因此，方程(1)描述的相分离过程可以简化为求解关于ϕ1的C-H 方程：

2 CFPM-GPU 并行算法

本文主要考虑多元C-H 方程下高维复杂多相界面分离过程的纯无网格法模拟，基于CUDA 的单个GPU 并行计算，结合Wendland 权函数的优点[17]，拓展文献[24]中二维FPM 离散过程得到一种能够准确、高效模拟多元高维C-H 方程的CFPM-GPU 并行算法.

2.1 三维CFPM 离散格式

对带Neumann 边界条件(2)含四阶导数三维C-H 方程(5)的求解，拓展应用文献[24]里对二维情况下单个C-H 方程连续应用两次FPM 的离散过程，时间更新采用二阶预估校正格式.基于Taylor 展开和加权最小二乘思想的FPM 主要用来离散函数空间一阶/二阶导数，其详细离散过程参见文献[25-27].相对于网格类方法，纯无网格FPM 更易实施非均匀或局部加密节点分布计算的优点也已在文献[24]中对二维问题进行了详细分析.文献[24]中FPM 离散过程采用样条权函数，而根据文献[17]知，Wendland 权函数较样条函数具有更好的光滑性和较高的数值精度，本文的离散过程采用Wendland 权函数.

以三维空间上均匀布点为例，采用的Wendland 权函数[17]形式如下：

其中，r=|xj−x|为支持域半径，j代表位置点x处支持域内的相邻点，wd为权函数系数，其在二维、三维空间中分别为7/(64πh2)和21/(211πh3)，h为光滑长度，在离散节点不动的情况下常取h≈0.95d0(d0为离散点初始间距).

由文献[24-27]知FPM 离散过程中，对一个函数f(x)在计算区域的任意分布离散点x处的一阶/二阶导数的近似值，通过x点在其支持域内所有相邻节点xj(j=1,2,···,n)(n为相邻节点数)上进行Taylor 级数展开和加权最小二乘思想过程得到的一个线性方程组求解而获得，即需求的局部线性方程组为

其中，上标符号“T”为转置，MTWM为9×9的局部系数矩阵；a9×1为x处函数一阶/二阶导数形成的未知矢量，为所有相邻节点处与x处函数差和施加边界条件构成的已知矢量，对角线上元素为“w1,w2,···,wn,1” ；矩阵M(n+1)×9为

单位外法向量n=(nx,ny,nz).

本文数值模拟中函数f(x)为方程(5)中函数ϕ 或µ.值得注意的是，上述线性方程组的求解过程需要求解两次来得到四阶空间导数的近似值，再结合二阶精度的时间离散格式可得方程(5)中 ϕ1新时间层里的数值解，然后可得 ϕ2，该过程称为高维多元C-H 方程的CFPM 离散格式.

2.2 单个GPU 并行加速算法

众所周知，运用纯无网格方法或粒子法对高维问题的计算模拟中，为得到较高精度数值结果常需要上百万离散节点或粒子数，这将会导致巨大存储或较长时间计算的问题[15-20].根据文献[15,17-18]知，对不含全局大型系数矩阵的纯无网格法或粒子法易于并行实施以提高计算效率.为此，已有许多基于MPI 多CPU 并行技术或算法被提出以加速纯无网格方法的计算[17-18]，为提高加速比就需要更多的CPU，会使得计算硬件和服务器的管理成本增加.近些年来，随着计算机GPU 的发展和NVIDA 公司不断更新的CUDA 编程模型[16,18-20]，使得GPU 能够进行大规模的并行计算，比如不涉及系数矩阵的纯无网格粒子法(SPH 或耗散粒子动力学法(DPD))的计算模拟已被成功地与GPU 并行计算技术结合发展了高效的并行算法 (详见文献[16,18-19,23])，且单个GPU 的并行计算加速比可以达到100 及以上(与单个CPU 串行计算相比)，但一个GPU 小工作站的管理成本远远低于有上百个CPU 工作站的管理.

纯无网格FPM 在高维多相分离过程的模拟还处在发展探索阶段，其并行算法实施的研究更是鲜有文献报道.本文首次考虑了基于CUDA 的单个GPU 来实现上述多元C-H 方程CFPM 离散格式的并行计算以提高效率，发展了CFPM-GPU 并行算法.在CFPM 离散格式的实施过程中涉及较大计算量或长时间计算的主要有两个方面：① 相邻节点的标定[23]，在时间层更新前每个节点i(对应位置xi，i=1,2,···,N，N为离散节点数)都需要通过搜索所有离散节点确定其支持域内相邻节点(每个点的相邻节点数不尽相同，其与离散点分布情况和位置有关系，本文数值模拟过程中离散点位置不变，故模拟实施中只需要循环一次相邻节点的标定)，随着离散节点数的增加该标定的计算时间也会变大(值得注意的是，本文数值模拟中节点或粒子位置在计算中固定)；② 在每个时间层的物理量更新中，N个离散点处空间导数的计算以及函数值的更新在串行编程实施过程中需要循环N次，包括局部矩阵的形成和求解，随着离散点数N的增大将会导致物理量每更新一次将需要较长时间的计算，但该循环可以同时并发进行(完全不依赖网格方法的特点).鉴于此，并行算法思想是重点对相邻节点编号标定和每次物理量更新中每个离散点处导数模型的循环实施并发性的计算.为实施CPFM 离散格式的GPU并行计算(并行算法较单个CPU 的加速比可见4.3 小节的讨论)，本文采用基于CPU 和GPU 的异构计算框架，其中以一个CPU 为主处理器(程序中常用host 表示)和一个GPU 为并发性计算实施的协处理器(程序中常用device 表示)，具体实施以CUDA-C + + 编程语言为主.另外需要注意的是，CFPM 格式中含9×9局部矩阵的形成和求解，其局部矩阵形成与相邻节点有关，在单个CPU 上串行计算实施时可以采用向量vector 的动态方式定义二维数组，准确地标记每个离散点处的相邻节点编号及相邻节点数，则在物理量更新计算的循环语句中形成局部矩阵时也需要用动态指针定义方式.但在GPU 并行计算实施中发现，将上述串行实施采用的动态指针方式来定义计算循环里的局部矩阵会使得GPU 内存不足，导致程序计算运行的阻塞.因此，在GPU 并行算法编程中需要首先用常量的方式来给出最大相邻节点数(估计值)，然后动态定义一个一维或二维数组来标记相邻节点编号，同时在物理量更新计算的循环语句中可用静态方式来定义局部矩阵的形成.

一个离散模型需消耗CPU 计算的实际时间，除了与编程语言和算法流程实施有一定关系外，受计算硬件性能指标的影响也很明显，本文数值模拟中采用的并行服务器工作站的主要硬件参数为：Intel Xeon Silver 4214 型号的CPU 处理器两颗，每颗CPU 处理器12 核心24 线程，主频为2.2 GHz，动态加速频率为3.2 GHz；三星DDR4-2666 的内存共128 GB；一个NVIDIA Geforce Titan RTX 型号的GPU，其显存容量为24 GB，核心频率1770 MHz，CUDA 核心数4608 个.本文给出的CFPM-GPU 并行算法流程可简化为如下几个步骤：

1)选定光滑长度h和时间步长dt，并用常量定义方式给计算中需要的一些参数变量赋值.值得注意的是，考虑计算区域 Ω为长方形或长方体 (相分离发生在一个复杂非规则区域内且对 Ω进行离散得节点数为N，其中上离散点采用均匀分布情况，上离散节点可根据其形状特点进行非均匀布点方式，但相邻两个节点的距离近似等于均匀布点的情况(比如圆形或球体上可以采用圆形或球形方式布点，也体现了本文采用的纯无网格法可以任意布点的优点).

2)动态方式定义所需的变量分配相关变量的host 内存及数据初始化，其中对函数 ϕ3赋初值(计算中不变)，函数 ϕ1和 ϕ2赋初始时刻的值；分配device 内存，并把host 上数据拷贝到device 上(CPU 到GPU)；调用CUDA 核函数在device 上并行方式运算标记出相邻节点的编号，便于后面物理量随时间更新循环运算.

3)当Nnum=1 时(设Nnum为计算时间层数，实际时间t=dt×Nnum)，调用两次CUDA 核函数在device 上并行实现方程(5)右端项CFPM 格式的运算，并结合时间项格式的第一步，得到每个离散点处函数 ϕ1,i的第一个中间值其中包括局部矩阵形成和调用在device 与host 上都编译的求解线性方程组的子函数.

4)结合时间项格式的第二步重复步骤3)的运算，将得到每个离散点处函数 ϕ1,i的第二个中间值.5)通过上述得到的两个中间值结合时间项上采用的预估校正格式的第三步，调用CUDA 核函数在device(GPU)上并行得到Nnum=1 时间层上每个离散点处第一个函数值；然后把device 上的计算结果传递到host 上(GPU 上信息传到CPU 上).6)运用式(3)在host(CPU)上计算得到Nnum=1 时间层上每个离散点处第二个函数值，然后再把host 上结果传递到device 上.

7)重复步骤3)～6)可以得到下一个时间层上每个离散点上的函数值 ϕ1,i和 ϕ2,i.

8)根据需要输出指定时间层上的计算结果.

3 CFPM-GPU 并行算法有效性验证

文献[24]主要对FPM 离散格式求解二维单分量C-H 方程的数值收敛性进行了分析，但未对多分量CH 描述的明显相分离过程以及三维C-H 方程进行数值研究.本节采用文献[8]中具有二维圆环和三维球壳收缩相分离过程的两个基准算例，对给出的CFPM-GPU 算法求解带Neumann 边界二维/三维C-H 方程的准确性和高效性进行分析，从而验证本文算法捕捉相分离过程的有效性.

文献[8]中两个相分离的基准算例没有理论解析解，其通过坐标变换给出了高精度的数值解作为基准解，并列出了某一时刻64 个网格点上的基准解(详见文献[8]中表1 和表3)用来进行误差分析.为了体现本文算法的准确性，参照文献[8]中误差分析方式，则有：

二范数误差

和最大范数误差

其中，d为空间维数，表示本文方法数值解和文献[8]中的基准解.

本节数值模拟二维圆环和三维球壳收缩过程对应的C-H方程可详见文献[8]，其中势函数F(ϕ)=0.25(ϕ2−1)2，梯度能量系数值得注意的是，为与文献[8]中的基准解做对比，本节数值模拟中的离散点均采用的是均匀分布方式，且离散点间距(空间步长)d0=1/64.

3.1 二维圆环收缩过程模拟

考虑二维空间区域Ω=(−1,1)2下圆环收缩现象，并将区域均匀离散成N=129×129个点，对应节点间距d0=1/64，时间步长取运算结束时间取T=8 000 000dt≈2.384.选取初始时刻函数：

经物理量更新循环8 000 000时间步运算，本文CFPM-GPU 法得到的数值解与基准解(见文献[8]中表1)的二范数误差E2=0.003 39，最大范数误差E∞=0.004 96.上述表明，本文方法求解二维圆环收缩过程对应的C-H 方程是准确稳定的，得到的圆环收缩现象也是可靠的.图1 给出了三个时刻二维圆环收缩现象的CFPMGPU 数值结果，其与文献[8]中图6 数值结果吻合.从图1 中可以看出圆环外圆与内圆随时间延长逐渐缩小形成圆环的收缩过程，结合上述算法误差精度可知，圆环的内外圆半径随时间延长的变小过程与文献[8]的基准解一致，从而体现本文给出的CFPM-GPU 法模拟二维情况下相分离过程是准确有效的.

图1 二维圆环收缩现象CFPM-GPU 数值模拟结果：(a)t=0；(b)t=1.31；(c)t=2.38Fig.1 The 2D shrinking annuli obtained with the CFPM-GPU:(a)t=0;(b)t=1.31;(c)t=2.38

3.2 三维球壳收缩过程模拟

三维球壳收缩过程对应的是球对称的C-H 方程，数值模拟中考虑三维空间域Ω=(−1,1)3，并将区域均匀离散成N=129×129×129个点，对应节点间距d0=1/64，时间步长取运算结束时间取T=400 000dt≈1.192.选取初始时刻函数：

经400000 时间步运算，CFPM-GPU 法得到t=1.192 时刻的三维球壳收缩现象，并与初始时刻结果做对比(见图2).图2 给出了两个时刻三维球壳收缩形状和二维截面圆环，其展现出明显的三维球壳收缩现象与文献[8]中图10 结果吻合.为体现本文方法数值求解的准确性，将沿半圆环线上的数值结果与基准解(见文献[8]中表3)进行对比，得到二范数误差E2=0.005 4和最大范数误差E∞=0.007 81.通过上述数值误差和三维球壳收缩现象表明本文方法模拟三维相分离过程准确.

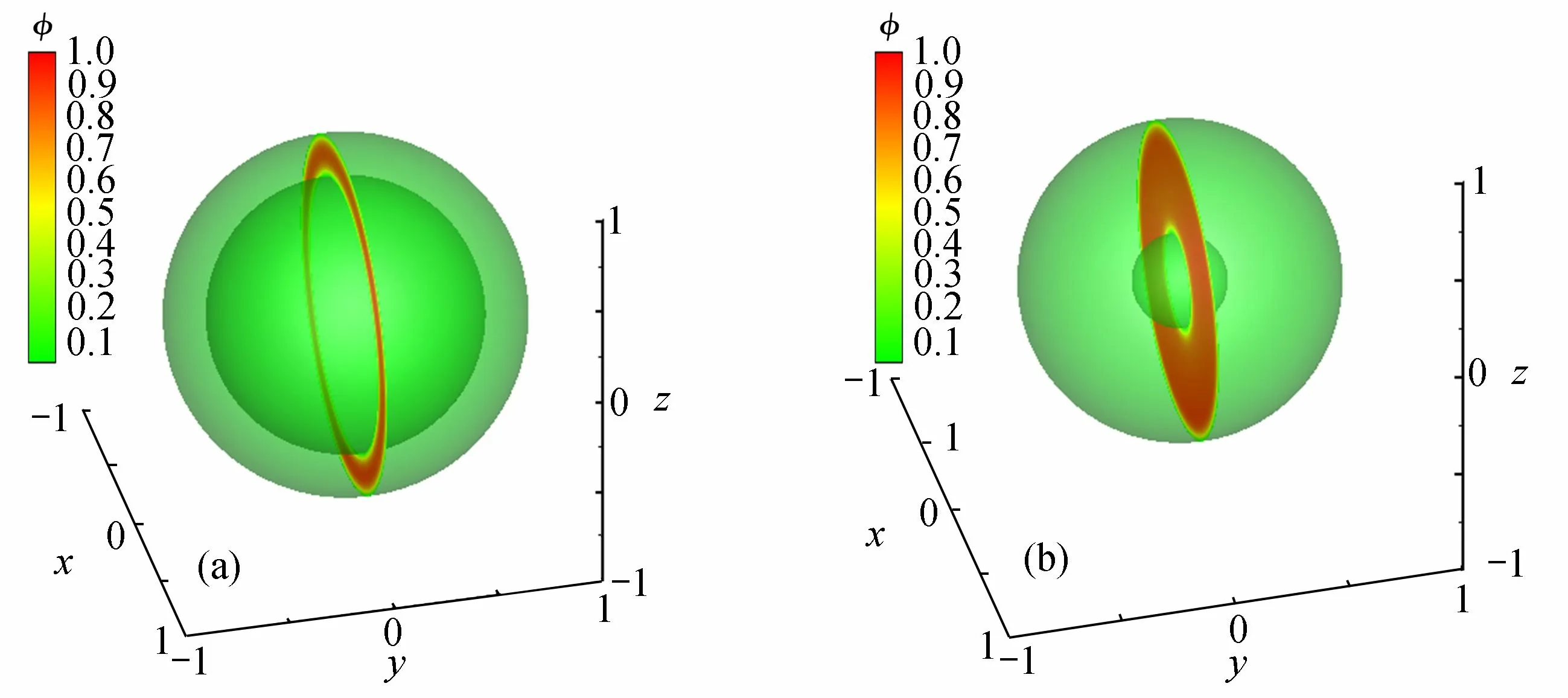
图2 三维球壳收缩现象CFPM-GPU 数值模拟结果：(a)t=0；(b)t=1.192Fig.2 The 3D spherical shells obtained with the CFPM-GPU:(a)t=0;(b)t=1.192

3.3 GPU 并行算法加速比分析

为体现本文基于CUDA 的单个GPU 并行算法的高效性，将其与单个CPU 的串行计算时间进行对比，关于GPU 并行服务器的性能参数见2.2 小节.为体现并行算法的效果，采用3.2 小节三维C-H 方程的算例，并定义加速比：

其中，tC表示单个CPU 计算消耗的时间，tC-G表示单个CPU-GPU 异构并行计算消耗的时间，δSur为加速比.

根据2.2 小节里并行算法思想的讨论，需要并行加速提高计算效率的有相邻节点标定和物理量更新循环两个部分，表1 和表2 分别给出了相邻节点标记消耗计算时间和每个时间层里物理量更新循环所需平均计算时间及加速比.由表1 和表2 知，随节点数增加，单个CPU 计算时间和GPU 并行计算时间也都随之非线性增加，但GPU 并行消耗计算时间远少于CPU 计算时间，表明基于CPU-GPU 异构并行计算较单个CPU 串行提高运算效率是显著的，且GPU 并行算法的加速比约为160.

表1 不同节点数下，相邻节点标定消耗计算时间对比Table 1 The consumed computing time for the calibration of neighbor nodes under different node numbers

表2 不同节点数下，每个时间层里物理量更新循环所需平均计算时间对比Table 2 The average computing time costs at each time step under different node numbers

4 二维/三维多相分离过程数值预测

为进一步体现本文给出的CFPM-GPU 并行算法数值模拟高维复杂区域上多相分离现象(m相分离情况对应m+ 1 元C-H 方程)，本节选取5 个代表性的复杂区域上的相分离算例[10]，其中包含3 个二维算例(圆盘域内和脑切面域内二相分离，星形域内三相分离)和2 个三维算例.

4.1 二维多相分离现象数值预测

算例1二维圆盘域上二相分离现象

其中rand(x,y)表示介于−1 和1 之间的随机数.选取节点间距为d0=1/512，时间步长为dt=10−6.运算到1 05时间步(对应时间t=105dt)结束，图3 给出了几个时刻下圆盘域上二相分离现象的CFPM-GPU 模拟结果，其中蓝色为 ϕ1，红色为 ϕ2.通过图3 可观察到在较短时间里(约t=0.05)就出现了明显的相分离现象，且随时间延长相分离越来越明显.本文结果与文献[10]中图3 的多重网格法得到的二相分离过程趋势一致，表明本文CFPMGPU 法模拟预测二相分离现象是可靠的(注意，两者间存在的差异主要由随机数rand(x,y)生成的初始值不完全相同导致).

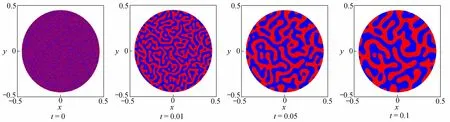
图3 二维圆盘域上二相分离现象CFPM-GPU 模拟结果Fig.3 The 2-phase separation obtained with the CFPM-GPU in the 2D disk domain

算例2二维脑剖面域上二相分离现象

为进一步体现本文方法模拟较复杂区域上二相分离现象的能力，将文献[10]中二维脑剖面轮廓形成区域视为发生二相分离的复杂区域，并嵌入到单位计算区域Ω=(−0.5,0.5)×(−0.5,0.5)内.图4 给出了二维脑剖面原图及复杂脑剖面轮廓作为区域，并通过图像处理技术和迭代计算得到模拟的初始值具体步骤如下：第一步，将脑剖面轮廓图4(b)拷贝到画图工具里，设置像素大小为512 × 512；第二步，用MATLAB 处理图像命令读取第一步里的RGB 像素矩阵，并输出到一个txt 文件里；第三步，通过编程对第二步得到的数据进行0-1 化处理，得到另一个txt 文件，将其作为模拟初始数据的估计值；第四步，将第三步里得到的数据代入到C-H 方程中，经过10 次迭代运算得到的值作为模拟初始的数据.模拟中初始时刻函数值除了 ϕ3，其他两个与上述算例1 的相同.对单位计算区域采用离散节点513×513，时间步长dt=10−6，经1 05时间步运算结束.图5 给出了CFPM-GPU 并行算法模拟的二维复杂脑剖面域上随时间演化的二相分离过程，其中蓝色为 ϕ1，红色为 ϕ2.通过图5 可知，本文方法能够模拟复杂区域上的二相分离现象，且与文献[10]中图5 结果趋势一致(两者存在差异的主要原因在于随机数产生的初始值不完全相同)，进一步表明CFPM-GPU 模拟预测复杂区域上二相分离现象是有效的.

图4 二维脑剖面原图及其复杂脑剖面轮廓[10]：（a）脑剖面原图；（b）脑剖面计算区域图Fig.4 The 2D brain section picture and the complex brain shape domian[10]:(a)the brain section picture;(b)the brain section calculation domain

图5 二维脑剖面域上二相分离现象CFPM-GPU 模拟结果Fig.5 The 2-phase separation obtained with the CFPM-GPU in the 2D brain shape domain

算例3二维星形域上三相分离现象

许多物理问题系统中存在多组分的三相分离现象，比如多相合金和三元纳米线制备中[28].因此，本节考虑了在单位计算区域Ω=(−0.5,0.5)×(−0.5,0.5)内星形域上三相分离过程的CFPM-GPU 法模拟，对应四元CH 系统的求解.四元混合物中各个分量ϕi(x,y,t)(i=1,2,3,4)同样满足质量守恒律ϕ1+ϕ2+ϕ3+ϕ4=1，且星形域各个分量初始条件为

其中θ=tan−1(y/x)且x≠0，随机数rand(x,y)同上.值得注意的是，ϕ1和 ϕ2的初始值表达式相同，但编程计算时使其取的随机数值不完全相同，且计算中需要求解关于 ϕ1和 ϕ2的C-H 方程组.采取的计算节点数与时间步长同上，经1 06时间步运算得到几个不同时刻的三相分离现象(见图6).观察图6 可知，在t=0.1 时刻出现了明显的三相分离现象，随时间演化三相分离现象越来越清晰(红色区域为 ϕ1，蓝色区域为 ϕ2，绿色区域为 ϕ3)，表明本文方法模拟预测非规则区域上三相分离过程是有效的.

图6 二维星形域上三相分离现象CFPM-GPU 模拟结果Fig.6 The 3-phase separation obtained with the CFPM-GPU in the 2D star domain

4.2 三维多相分离现象数值预测

算例4三维环形体域上相分离现象

为体现CFPM-GPU 法模拟三维复杂域上相分离现象的有效性，考虑三维环形体域上二相分离，取环体区域嵌入在计算区域Ω=(−0.5,0.5)×(−0.5,0.5)×(−0.25,0.25)内.三元C-H 方程中每个分量的初始条件为

其中随机数rand(x,y,z)同上.

模拟中采取离散节点129×129×65，初始间距d0=1/128和时间步长为dt=10−6.图7 展示了本文数值方法得到的关于 ϕ1三个时刻的相分离现象，在较短时间t=0.01 时就出现相分离，随时间演化相分离现象越发明显，且与文献[10]中图7 结果趋势一致.

图7 三维环体域上相分离现象CFPM-GPU 模拟结果Fig.7 The phase separation obtained with the CFPM-GPU in the 3D torus domain

算例5三维Schwarz-D 域上相分离现象

为进一步体现CFPM-GPU 法模拟三维复杂域上相分离现象的可靠性，考虑Schwarz-D 形域[10]嵌入在计算域Ω=(0,1)×(0,1)×(0,1)的二相分离，其中发生相分离的复杂Schwarz-D 形域三元C-H 方程中每个分量的初始条件为

其中

C(x,y,z)=cos(2πx)cos(2πy)cos(2πz)−sin(2πx)sin(2πy)sin(2πz).

模拟中采取离散节点129×129×129，初始间距和时间步长与算例4 相同.图8 展示了三维复杂Schwarz-D 形域上CFPM-GPU 法模拟的相分离现象，可观察到在较短时间t=0.01 时就出现明显的相分离现象，本文数值结果与文献[10]中的相分离趋势一致.

图8 三维Schwarz-D 区域上相分离现象CFPM-GPU 模拟结果Fig.8 The phase separation obtained with the CFPM-GPU in the 3D Schwarz-D domain

通过算例1～算例5 二维/三维复杂域上相分离现象的CFPM-GPU 模拟，并与文献[10]中图8(b)结果比较可知：本文提出的CFPM-GPU 求解三元或四元C-H 方程组是有效的；CFPM-GPU 数值预测二维/三维复杂域上的二相或三相分离现象是高效可靠的.

5 结论

本文针对二维/三维复杂域上多相分离现象的高效性与准确性模拟，首次结合CPU-GPU 异构并行计算、拓展求解含四阶导数二维C-H 方程的FPM 和采用具有较好光滑性的Wendland 权函数，给出了一种基于CUDA 语言单个GPU 的CFPM-GPU 并行算法.为体现CFPM-GPU 模拟预测复杂域上多相分离的有效性，首先运用CFPM-GPU 分别对两个相分离的基准算例(二维/三维)进行了模拟，并对误差和并行加速效率进行了分析；其次，用CFPM-GPU 对无解析解的多个二维/三维复杂域上的二相或三相分离现象进行了数值预测，并与多重网格法结果比较.所有数值结果表明：

1)本文的CFPM-GPU 并行算法求解二维/三维C-H 方程描述的相分离过程是准确、高效的；

2)基于CUDA 的单个GPU 并行较CPU 串行运算的加速比约为160 倍；

3)给出的CFPM-GPU 能准确预测二维/三维复杂区域上二相或三相分离现象随时间的演化过程.

致谢本文作者衷心感谢扬州大学本科专业品牌建设与提升工程项目(ZYPP2018B007)对本文的资助.