预混燃烧边界层回火的数理模型及研究进展*

李文栋，张文普

（浙江大学 航空航天学院，杭州 310027）

引言

燃气轮机、锅炉和内燃机等动力机械需要通过燃烧过程将燃料的化学能转化为机械能，而燃烧过程的组织方式，即燃烧方式，可依据燃料和氧化剂在反应前是否充分接触混合，分为扩散燃烧和预混燃烧，扩散燃烧由于其火焰稳定性高等优势得到了广泛的应用，但是难以避免氮氧化物等污染物的大量产生.近年来，随着科技和工业的发展，人类意识到以破坏生态和污染环境为代价换来的发展是不可持续的，人们的环境保护意识逐步增强，陆续出台了大量控制污染物排放的法律法规.因此，在动力机械及设备的研究与设计中，低污染燃烧与排放技术逐步成为必须发展的核心问题和关键性技术.相比于扩散燃烧，预混燃烧需要在燃烧之前将反应物气体混合均匀，可以通过调整燃料与氧化剂的掺混比，来控制燃烧的温度，使燃烧装置的工作温度低于氮氧化物等污染物成分的生成温度，从而降低氮氧化物等污染物的生成率[1].

预混燃烧技术虽然有许多优点，但是相比于扩散燃烧，很多时候会出现火焰从燃烧室向上游传播并进入预混区的现象，即回火现象.回火的发生会破坏燃烧的稳定性，这样非但达不到预混燃烧原有的技术优势，还会引起燃烧器结构破坏等严重后果[2].因此，想要燃气轮机平稳运行，必须避免回火的发生，需要对其发生的机理和条件进行深入理解和研究.

1 回火机理

目前已知的回火机理主要有以下四种：中心流回火、燃烧不稳定引发回火、燃烧诱发旋涡破碎引发回火及边界层回火.

中心流回火[3]是指在燃烧过程中，与中心流的局部流速相比，若燃烧速度更大，则火焰可能在中心流向上游传播.燃烧不稳定引发回火[4]是由流场的大幅度振荡造成的，流场振荡由不稳定燃烧所诱发，同时又与不稳定燃烧相互作用，这一过程涉及到声学、热释放和流场结构之间的相互作用.燃烧诱发旋涡破碎引发回火主要出现在旋流燃烧器中[5]，旋涡破碎的产生是由于旋流数超过了一定值[6-7]，从而引发回火.

对于第四种回火机理——边界层回火，近年来燃气轮机越来越广泛地使用富氢燃料，这类富氢燃料具有较高的火焰速度与相对较小的熄火距离，导致在燃气轮机燃烧室内更容易发生边界层回火现象，因此针对边界层回火的相关研究也变得愈发重要.在正常运行的条件下，燃气轮机燃烧室中心区域来自预混器的气流速度大于火焰传播的速度，不会发生回火.但是在靠近壁面处的气流流速会降低，在一定条件下，当火焰传播速度大于壁面附近的气流速度且小于中心区域的气流速度时，尽管不会产生中心流回火，但火焰依然会向上游传播，边界层回火由此发生.研究人员最初为了研究边界层回火倾向发展了经典的临界梯度模型(critical gradient model，CGM)，但近年来随着研究的逐步深入，实验和数值研究揭示了这一经典模型存在一些局限和不足，并据此发展了新的理论模型.

2 理论模型

2.1 CGM 及其衍生模型

Lewis 等[8]在20世纪40年代通过对边界层回火的实验，发展了经典的CGM.如图1所示，图中δq和δp分别为熄火距离和渗透距离，临界速度梯度可表示为

图1 CGM 示意图Fig.1 Schematic diagram of the critical gradient model

式中，gc为临界速度梯度，τw为切应力，µ为动力黏度，SL为层流火焰传播速度.CGM 假定在回火发生时，流速分布不受火焰影响，且在壁面附近流速是线性的，其对于层流边界层回火可以较为准确地预测回火倾向，这一模型的出现奠定了边界层回火研究的理论基础.

Putnam 等[9]于20世纪40年代末在CGM 的基础上，应用无量纲数来预测回火，提出了Peclet 数模型(Peclet number model，PNM)：

式中，PeJ和PeF分别表示基于回火时来流平均速度的Peclet 数和基于火焰传播速度的Peclet 数，C为比例系数，为回火时的来流平均速度，λ 为热传导系数，d为管道直径.

该模型引入Peclet 数的目的是想通过无量纲数使得CGM 得到应用范围上的扩展，但从本质上而言，PNM 其实是基于CGM 的一个衍生模型，因此，我们将其归类于CGM.

瑞士保罗谢尔研究所(Paul Scherrer Institute，PSI)的研究人员Lin 等[10]在研究边界层回火时发现，在回火即将发生的临界状态下，湍流火焰速度与壁面附近的局部流速几乎一致，于是将湍流火焰速度应用于CGM 得到

式中ST为湍流火焰速度，δf为火焰厚度，Le为Lewis 数，通过Lewis 数可以捕捉到混合物中的氢气成分对于回火的影响.虽然Lin 等的实验装置中没有直接安装在燃烧器顶端的专用热电偶，但在燃烧器入口上游的位置，对燃烧器头部温度进行了监测.且由于用水冷却了燃烧器头部，该实验的研究者认为燃烧器头部的温度不会对回火极限预测造成明显影响.与CGM 相比，该模型对于湍流火焰速度和火焰厚度等参数的引入提高了在湍流边界层回火下的适用性.

CGM 及其衍生模型作为边界层回火研究领域的经典理论模型，模型简单，能够快速且比较准确地预测回火现象的产生、发展及火焰的回火特性，应用相对比较广泛，但是由于建模过程中忽略了一些比较重要的因素，因而存在一定缺陷和局限性.Eichler 等[11]的实验研究以及Gruber 等[12]的数值研究都发现：在CGM 中被忽略的火焰-流场相互作用对回火现象的生成与发展具有重要影响，CGM 忽略了这一相互作用的影响，降低了模型的预测效果.

李宇斌[13]也在针对层流平板流动的氢气-空气边界层回火数值研究中验证了CGM 的局限性，他针对图2所示的平板流动，对于氢气的单步总包反应机理和10 组分21 步详细化学反应机理分别进行了数值计算.计算结果一方面验证了：在层流条件下，CGM 能够快速且比较准确地预测层流火焰的回火特性；另一方面，计算结果也表明：火焰-流场间的相互作用对回火的产生与发展有着重要影响，CGM 对这一相互作用的忽略影响了其预测的准确性.他在计算过程中发现逆流区存在“回流泡”，“回流泡”在向上游运动的同时促进了火焰的回火，这说明火焰-流场相互作用对于回火有着重要影响，CGM 未考虑火焰对于流场所产生的影响，无法准确预测及发现“回流泡”等边界层回火过程中的真实物理现象.在李宇斌的研究中还发现，当火焰前缘产生逆流区时，壁面温度并未达到临界分离温度，从而认为火焰-流场之间的相互作用在火焰前缘产生的压升是逆流区产生的重要因素，进一步表明，火焰-流场间的相互作用对回火的产生与发展有着重要影响.此外，CGM 在一维条件下的动量守恒对于数值计算过程中化学反应发生时壁面的升压变化也难以作出解释.

图2 计算域示意图Fig.2 Schematic diagram of the computational domain

2.2 Damköhler 数模型

针对CGM 及其PNM 的不足和局限性，后续的学者陆续对此类模型进行了一些补充性的研究工作.自提出PNM 以后的几十年间，理论模型未有较大的发展.直到21世纪，Kurdyumov 等[14-15]提出了Damköhler 数模型(Damköhler number model，DNM)，依靠这一模型可以实现对边界层回火更加准确的预测：

式中Dc为临界Damköhler 数.与CGM 相比，DNM 还额外引入了火焰厚度等相关参数，这为后续理论模型的改进提供了一些新的思路.

在Kurdyumov 等提出DNM 之后，Kalantari 等[16]进一步通过实验研究了在高压(3 ～ 8 atm)、高温(300 ～500 K)和湍流条件下，预混射流火焰的回火倾向.Kalantari 等基于量纲分析的π定理，根据Duan 等[17]在大气压下基于不同燃料组分和燃烧器材料下的DNM，将其拓展到高压条件，建立了一个新的综合的无量纲模型：Damköhler 关联(Damköhler correlation，DC)模型，并且与文献[18]中高压条件下的实验数据相比无较大误差.该模型Damköhler 数的具体表达式如下：

式中Tu为未燃混合物温度，T0为参考温度，其值为300 K，TB为燃烧器边缘温度，Pu为环境压力，P0为参考压强，其值为1 atm.

与之前的PNM 和DNM 相比，DC 模型拓展了在湍流射流火焰，尤其是高压和富氢燃料条件下的回火研究.DC 模型具有输入参数数量适中、计算复杂度较低等优势，有较高的可用性.Kalantari 等[19-20]在商用65 kW微型涡轮发电机上证明了该方法的适用性.

Kalantari 等[21]还将此方法与2.1 小节中提及的PSI 应用湍流火焰速度的CGM 进行了比较：该模型的一个重要局限性是没有充分考虑到火焰前锋和燃烧器之间的热耦合效应，而DNM 对于火焰前锋和燃烧器之间的热耦合效应则有所考虑，这更加贴合燃气轮机在工程应用中的实际情况.

2.3 火焰角度理论

在CGM 提出七十余年之后，Hoferichter 等[22]提出了一个与CGM 及其衍生模型都截然不同的新的边界层回火模型.

对于如图3所示的非受限空间火焰的回火情况，Hoferichter 等[22]在Baumgartner 等[23-24]对预测模型初步描述的基础上，建立了“火焰角度理论”(flame angle theory，FAT)，火焰角度αFB在这一预测模型中起关键作用.该理论对于回火起始的局部分析和整体分析如图4 和图5所示，回火火焰形状假设为三角形或者锥形.

图3 非受限空间的边界层回火Fig.3 The unconfined boundary layer flashback

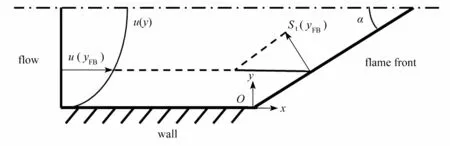
图4 非受限空间火焰的局部分析Fig.4 Local analysis of the unconfined flame

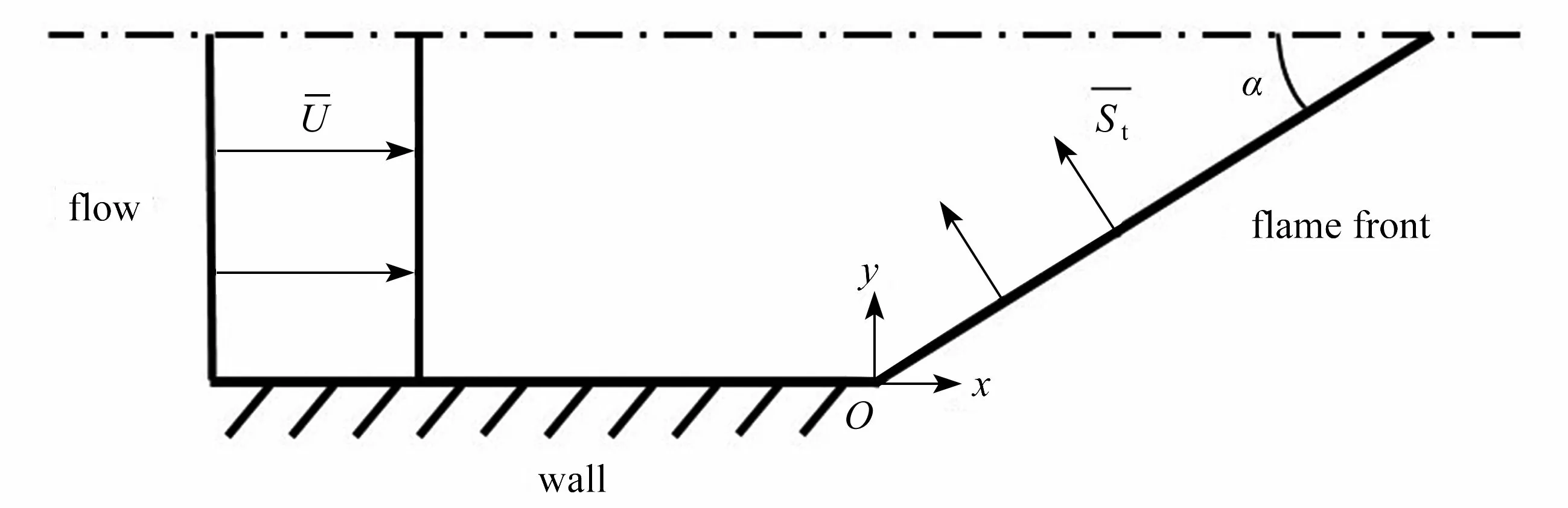
图5 非受限空间火焰的整体分析Fig.5 Global analysis of the unconfined flame

分析牵涉到以下7 个方程[22]：

式中S为燃烧速度，下标中，l 和t 分别表示层流和湍流，0 和s 分别表示未拉伸和拉伸，FB 表示回火情况，u为平行于壁面的速度分量，y为垂直于壁面的距离，Cs为湍流燃烧速度关联系数，u'为湍流速度脉动，LM为Markstein 长度，ΓK为ITNFS (intermittent net flame stretch)模型效率函数，Λ 为湍流宏观尺度，δF为层流火焰厚度，uτ为剪切应力速度，u+为归一化速度为归一化壁面距离 (uτy/ν)，为平均流速，B为壁面对数律参数，其值为5.0，K为von Kármán 系数，其值为0.41，h为燃烧器高度或直径，ν 为运动黏度.

通过分析方程数目和未知量数目，可知上述7 个方程中，有8 个未知量：St，u，u′，αFB，Sl,s，ΓK，uτ，.为了使这组方程封闭可求解，需要另外确定参量火焰角度αFB.为求解αFB，Hoferichter 等[22]基于整体质量守恒，建立了以下6 个方程：

式中G1～G4为火焰-湍流关联系数.先根据方程(13)～ (18)求得火焰角度αFB，然后在αFB已知的条件下对方程(6)～ (12)进行求解，这样就可获得回火极限UFB.

Hoferichter 等[22]还通过槽道和管道燃烧器的实验对FAT 模型进行了验证，研究发现：在贫燃条件下有一定的误差，来源于混合物中燃料的局部富集现象的影响造成的高度不确定性，这是由氢气在氧气中比较高的扩散率所导致的，特别是一旦与火焰拉伸这一影响因素相结合，会导致火焰传播更快.由于FAT 基于回火的物理过程进行分析，因此其适用条件十分广泛.

Hoferichter 等[25]对DC 和FAT 这两种理论模型进行了分析比较，选取的工况是直径为25.4 mm 的管道燃烧器[16]，依据所得的Damköhler 数进行比较.如图6所示，当量比范围为0.35 到1 之间，其中较低的当量比对应于较低的层流燃烧速度，也就对应于较低的Damköhler 数，反之亦然.图中的实线表示DDC和DFAT相等的理想情况，虚线表示实验所得数据[16]的波动范围，可以看出在当量比较低（即Damköhler 数较低）的情况下，DDC比DFAT小；而在当量比较高的情况下，DDC比DFAT大.也就是说式（5）对于Damköhler 数的预测在低当量比的情况下偏小，而在接近化学当量的情况下偏高，这可能是由于DC 模型没有考虑到火焰拉伸这一影响因素所导致的.因此，Hoferichter 等[25]依据FAT 模型对于DC 模型进行改进，得到修正Damköhler 关联(modified Damköhler correlation，MDC)模型.MDC 模型中的Damköhler 数表达式如下：

图6 依据DC 模型和FAT 模型获得的Damköhler 数[25]Fig.6 Damköhler numbers obtained from the DC and the FAT[25]

式中C1为模型系数，其值为2.731 × 10−4，ρ 为混合物密度，下标u 表示未燃状态.MDC 模型所预测的回火极限在大气压条件下与实验数据误差较小，而在高压条件下，虽然MDC 模型对于回火极限的预测准确性优于DC 模型，但是与FAT 模型的结果仍不能完全吻合.在后续的研究工作中，还需要在高压和高预热温度的情况下，对不同当量比射流燃烧器的回火极限进行实验研究，用于检验MDC 模型.

从模型建立过程来看，FAT 模型比较充分地复现了回火发生时的物理过程，广泛适用于非受限空间的边界层回火，但由于对于物理真实性的追求，该模型的数理方程十分复杂，因而实际应用性受到一定局限；DC 模型及MDC 模型则更注重于工程上的应用，输入参数相对简单，可用性较高，但准确性和适用范围则不及FAT 模型.

2.4 针对受限空间火焰的新理论模型

除了FAT 模型之外，Hoferichter 等[26]还针对受限空间火焰提出了新的理论模型.该模型的依据是Eichler 等[27]的研究发现：受限空间火焰的回火是由于火焰尖端上游处的边界层分离而引发的，而且Gruber 等[12]也通过DNS 研究证实了这一结论.因此只

要能确定引起边界层分离的受限空间火焰上游的最小压力上升，就可以预测回火极限.针对边界层分离，Hoferichter 等使用了Stratford 准则进行分析，这一准则是Stratford[28]为研究空气动力学现象中的边界层分离而开发的.Hoferichter 等基于该准则与湍流燃烧速度，通过以下8 个方程推导出满足引发边界层分离条件的燃烧器平均流速：

式中，Δp为未燃烧状态下与燃烧状态下的压强差，xf为火焰尖端位置，Tad为绝热温度，κ 为火焰拉伸率，lt为湍流宏观尺度，a0～a5为固定的系数.

Hoferichter 等[26]将该模型的预测结果与Eichler[29]在槽道燃烧器下的实验数据进行了比较，如图7所示.图中实心标记表示实验数据，空心标记表示依据模型所得的预测数据，从图中可以看出该模型的预测结果与实验结果保持了较好的一致性，证明了该模型对于受限空间火焰回火预测具有较高的准确度.

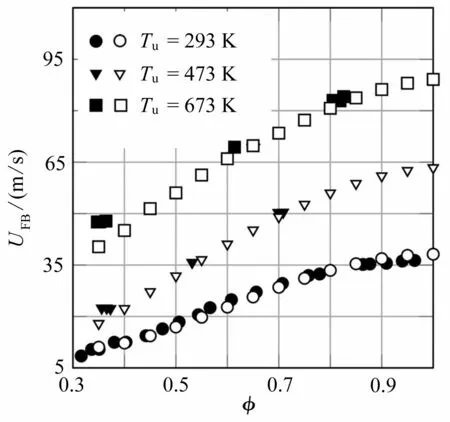
图7 预测回火发生时的流速与实验数据对比[26]Fig.7 Predicted velocities at flashback compared to experimental data[26]

2.5 边界层回火理论模型发展的回顾

CGM 对于流场和回火机理简洁高效的描述和本身简单易用的特点使其成为了边界层回火领域最为经典的理论模型，很长一段时间都被当作边界层回火理论模型的基石，不论是PNM 还是DNM，都是在其基础上所进行的补充.直到近年来随着实验和数值研究水平及精确性的提高，经典模型忽略火焰与流场相互作用的局限性逐渐被研究人员重视起来.针对这一问题，总结近年来的理论模型相关研究，可以看到有两种发展方向：其一是在无量纲数模型的基础上，为了满足燃气轮机在应用中对于回火预测的需求，进一步发展出如DC 模型等更加贴合实际情况，在真实的应用场景中更为准确，使用起来也十分简便高效的理论模型；其二是基于边界层回火的物理过程分析，建立如FAT 这样新的理论体系，突破了经典模型的局限性，虽然理论本身较为复杂，但是适用范围广泛，兼容性好，有广阔的发展空间.

3 实验研究

Lewis 等[8]建立CGM 的研究是有文献记载的针对边界层回火最早的实验研究之一[30]，在这一研究之后，即20世纪40年代之后的数年间也陆续出现了许多针对边界层回火的实验研究.Von Elbe 等[31]在大气压条件下，对于直径为0.108 ～ 0.33 cm 的燃烧器，测量了氢气燃烧的回火倾向.Garside 等[32]将边界层回火实验研究的压强条件拓展到了亚大气压.Edse[33]在最高达100 倍大气压的高压条件下，针对氢气和氧气混合物的湍流边界层回火，用本生灯火焰进行了实验研究.Grumer 等[34]针对预热温度对于回火极限的影响进行了实验研究，对象是甲烷/空气混合物.Bollinger 等[35]在大气压条件下，对氢气/氧气混合物火焰，研究了尖端温度对于回火的影响.

进入21世纪以后，边界层回火相关实验研究的数量就没有上个世纪那样迅速的增加了.Davu 等[36]在大气压和室温的条件下，研究了甲烷/空气混合物的回火倾向受燃烧器直径的影响.Dam 等[37]针对H2/CO 和H2/CH4混合物的层流边界层回火进行了实验研究，他们发现混合物的临界速度梯度随着H2浓度的增加而发生非线性变化，实验中还采用了不同的燃烧器直径，由此发现在贫燃条件下燃烧器直径的影响较小，但是随着当量比的增大，直径影响会变得更加明显.

Eichler 等[38]研究了甲烷/氢气/空气混合物的湍流边界层回火，使用一种实验装置捕捉到边界层回火过程火焰尖端的位置，然后依据经典的CGM 理论通过RANS 模拟得到临界速度梯度，但是结果与已有的管式燃烧器所测得的回火数据相差较大，这可能是由于逆压梯度对于边界层结构的影响导致的.Eichler 等[27]还对于氢气/空气在不同燃烧器结构下的边界层回火极限进行了实验研究，实验中采用了两种典型的燃烧器类型，管道燃烧器结构如图8所示，槽道燃烧器结构如图9所示.其中结构3 示意图中的数字表示两种不同的高度组合：第一种为左侧3.5 mm、右侧0.5 mm 的A 处结构；第二种为左侧2 mm、右侧2 mm 的A 处结构.研究得到不同工况下的回火极限结果如图10所示，可以看出受限空间火焰和非受限空间火焰的回火极限差别明显，Eichler 等认为这一结果的出现与不同工况下熄火距离的变化有关.该研究以前的边界层回火研究对象大多是管道燃烧器的非受限空间火焰，Eichler 等则通过此次实验研究证实了：火焰位置是边界层回火极限的关键影响因素之一，这也是该实验研究极具意义的重要发现.

图8 管道燃烧器示意图[27]Fig.8 Schematic diagram of the tube burner[27]

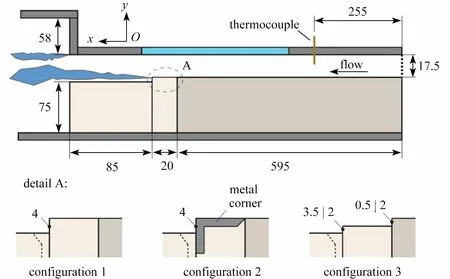
图9 槽道燃烧器示意图[27]（单位：mm）Fig.9 Schematic diagram of the channel burner[27] (unit:mm)

图10 不同燃烧器的边界层回火极限[27]Fig.10 Boundary layer flashback limits for different burners[27]

Duan 等[39-40]使用了不同的燃烧器材料（石英和不锈钢）进行研究，并且发现石英材料增大了边界层回火倾向，他们认为这是由于石英的热导率较低导致尖端温度升高.他们还针对不同的火焰结构进行了研究，并且认为不受限的火焰回火倾向更高，其原因可能是边界层加热，临界速度梯度的变化可能是尖端温度变化以及边界层加热的结果.

Hoferichter 等[41]针对热声不稳定性在燃烧器出口诱发速度振荡，进而引发火焰回火这一问题，进行了纵向声激励对管道燃烧器边界层回火影响的实验研究，用声激励模拟热声不稳定性的影响.激励幅度增大，回火发生的风险增加，这种效应在低频时最强.激励频率增大，速度振荡的影响减小.

Goldmann 等[42]在常温(293 K)和常压(101 kPa)下对预混的氢/氨/空气混合物的边界层回火进行了实验研究，介绍了一种新的实验装置，该装置采用全自动测量程序，首次研究了各种测量方法对回火极限的影响.

在边界层回火研究领域，不管是理论模型的建立，还是数值模拟的结果，往往都需要实验的验证才具有说服力.实验研究所针对的影响边界层回火的条件，包括了燃料组分、压力、预热温度、燃烧器尺寸与材质、流动状态等众多因素，现代的实验研究倾向于发掘一些未被广泛考虑的因素对于边界层回火可能造成的影响，比如热声不稳定性和测量装置及方法等影响因素.

4 数值研究

在20世纪80年代，Lee 等[43]的研究是有文献记载的针对边界层回火的第一批数值研究之一，模拟的是管道中的预混层流火焰的回火状况.研究发现随着管道直径的减小，临界速度梯度持续增加后骤减，这可能是由于熄火效应的影响.Lee 等[44]还研究了绝热壁和等温壁圆管中火焰的稳态传播，燃料为贫燃甲烷/空气混合物，他们发现在管内稳定传播的火焰呈现不同的形状，而且火焰的速度和形状都会受到重力的影响.随后的数年间，数值研究的方法被越来越多的研究者使用，研究对象包括非受限空间下甲烷/空气火焰的回火[45]、Poiseuille 流条件下绝热槽道中的火焰回火[46]、不同Lewis 数的预混层流火焰[47]等.

Gruber 等[12]采用DNS 方法研究了氢气/空气预混燃烧的回火现象，模拟的环境是充分发展的湍流槽道流.他们发现向上游传播的预混火焰的前锋始终位于近壁区域，火焰向反应物凸起.近壁回流区域的存在，以及流体动力学不稳定性和压力与流场间的相互作用，都对边界层回火有重要影响，其回火速度会随着压力的增加而增加.这一研究表明，CGM 忽略火焰与来流相互作用不能完整表现出回火机理.

Endres 等[48]研究了大涡模拟对于已经实验确定过的回火极限的再现能力，再现的对象是Eichler 等[27]的实验，燃烧过程通过有限速率化学和详细化学动力学进行模拟.结果表明，采用Smagorinsky 湍流模型的大涡模拟能够再现槽道流的湍流特性，所选择的燃烧模型再现了与边界层回火相关的所有物理效应.此外，当局部流动分离区的尺寸明显超过火焰的熄灭距离时，边界层回火现象开始出现，这与Eichler 等提出的假设相符合[29].该研究发展了使用LES 捕捉湍流边界层回火的研究思路，同时研究对象是受限空间火焰，对于更高的温度与压力下，亦或是非受限空间火焰的相关研究仍有待进行.

Gruber 等[49]针对湍流边界层回火中的火焰形状进行了DNS 研究，并开发了一个简易模型来预测火焰形状，该模型在贫燃或富燃条件下对于火焰形状都有一定的捕捉能力，但在贫燃条件下更为准确.Gruber 等[50]还针对燃烧反应物从均匀混合结构转变为分层混合结构的火焰结构与回火情况，在湍流边界层回火条件下进行了DNS 研究，这为从燃料对于回火倾向的影响这个角度出发的研究提供了新的思路，可以不仅是局限于燃料组分，还要考虑到燃料的分布.

曹敏等[51]针对贫油直喷燃烧室，采用LES 方法研究其回火特性.在精确捕捉到回火的动态过程后，研究发现贫油直喷燃烧室内会在强旋流的作用下形成中心回流区，回流区向上移动，从而促进了火焰向上游的传播，最终导致回火的发生.

Endres 等[52]对于氢气/空气的受限空间火焰回火中压力的影响进行数值研究.研究方案使用了有限速率化学和详细化学动力学的LES，0.05 ～ 0.3 MPa 下的扩散模型.研究发现随着压力的增大，回火倾向增大，但是回火条件下的分离区尺寸和湍流火焰速度减小(降低了回火倾向)，同时熄火距离减小(增大了回火倾向).所以仅仅根据湍流火焰速度或者分离区大小与熄火距离之比，无法预测边界层回火的发生，在模拟边界层回火时，必须考虑所有影响因素的相互作用.此外还发现，火焰前面的压力上升不能采用一维模拟，且在有约束边界层回火过程中，边界层理论的假设不满足.

Ding 等[53]研究了壁面粗糙度对于边界层回火的影响，其采用二维模拟来研究具有粗糙壁面的槽道中的层流边界层回火.如图11所示，该研究选用了三角形的粗糙结构，s和h分别表示粗糙元的高度和半长，其中s固定不变，通过更改斜率k=h/s来更改粗糙度，当然也会改变壁面面积.该研究使用非正交结构化网格，在保持结构化网格计算效率高等优点的同时，又能保证网格在粗糙壁面处的精确度，在粗糙结构附近采用多层四边形网格来反映壁面粗糙程度变化带来的影响.模拟结果表明，高的壁面粗糙度可以减弱回火倾向.更高的粗糙度会在近壁区形成更厚的流动停滞区，也会造成更大的热量损失，这增加了壁面附近的熄火距离和渗透距离，进而，临界速度梯度和火焰传播速度会发生变化：临界速度梯度随着壁面粗糙度的增大而减小，随着热膨胀系数的增大而增大；火焰传播速度随着粗糙度的增加而降低.该研究还比较了壁面处有热损失的模拟与绝热壁面的模拟，得出结论：当壁面的热阻较低时，由壁面粗糙度增加而导致的热损失强度变化，可能比来流参数的改变更重要.通过对回火临界条件的研究，发现来流剖面在火焰附近发生了很大的改变，而经典的临界速度梯度理论忽略了这一点.

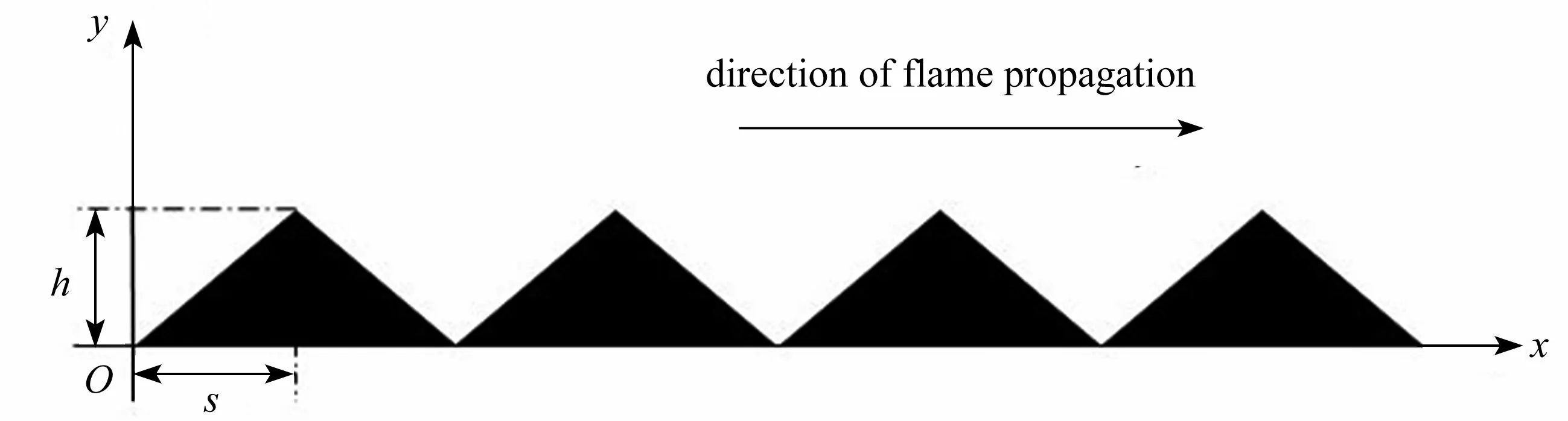
图11 粗糙结构示意图[53]Fig.11 Schematic diagram of the roughness configuration[53]

关于边界层回火的数值研究工作数量众多，其所得到的海量模拟数据作为重要的资源值得进一步发掘，Ahmed 等[54-55]应用统计分析的方法，对Kitano 等[56]关于回火的数值模拟数据进行分析，研究了火焰回火行为、湍流动能输运过程和反应进度变量梯度(也称为表面密度函数(surface density function，SDF)).Kitano 等[56]针对预混氢气/空气火焰边界层回火进行DNS 模拟，Ahmed 等则在Kitano 等模拟工作的基础上，应用统计方法分析了DNS 模拟中所得到的流场、湍流结构和火焰特性等，分析过程中还对比性地参考了Gruber 等[12]所进行的DNS 模拟数据.通过统计分析，Ahmed 等发现火焰传播到充分发展的湍流边界层上游时，会在上游区域引起逆流区域，这与Gruber 等[12]的早期研究发现相符合，并且逆流区域还导致了负的壁面剪切应力；统计分析还发现在回火条件下，压力膨胀和压力引起的湍流输运是湍流动能方程中的两个主导项，这与Lai 等[57]关于迎面熄火火焰的早期发现相吻合.基于Ahmed 等的工作可以看出，湍流动能输运方程未封闭项的模拟将成为未来边界层回火研究的方向之一.另外在关于反应进度变量(reaction progress variable，RPV)的研究中，Ahmed 等[55]将其定义为三种类型，分别基于H2、O2和H2O 的质量分数.研究发现，由于冷壁面的存在，近壁区域的膨胀效应减弱，并且随着离壁面距离的增加，SDF 与最大主应变率之间的一致性会增强.这就导致了在距离壁面的不同位置处，法向应变率和切向应变率的行为存在差异.同时研究结果和槽道流的Reynolds 数之间有一定相关性，未来还需要分析不同Reτ情况下的更多数据，以研究湍流的变化对SDF 的影响.

边界层回火数值模拟的目标，始终是在迅速发展的CFD 技术和众多的实验数据的辅助下，通过计算在数值上表现出边界层回火的动态过程与回火发生时的临界状态，得出回火极限的影响因素以更好地避免在燃烧装置中发生回火现象.可以看出，与实验研究相类似，初期的数值模拟着重针对燃料组分以及燃烧管径等常见的外部条件，且常用层流流动，然后在实验数据的验证下进一步确定这些参数对于回火极限的影响.近年来得益于计算机技术的迅速发展，边界层回火数值研究中能有效提供流场信息但是颇为消耗资源的DNS 方法逐渐成为主要的数值研究工具，以Gruber 等针对湍流情况的DNS 研究为代表，详细的DNS 研究数据也帮助研究人员发现了CGM 的局限性，这表明了数值方法已经成为研究边界层回火强有力的手段.大量的相关数值研究也证实了LES 方法具有捕捉回火现象的能力，可以再现回火的临界状态，LES 方法与DNS 方法相比在节省计算资源、减少计算时间的同时，还能够获取相对比较详细的流场与火焰特性.同时，现代的数值研究还能处理如壁面粗糙度等实验中难以频繁调整的影响因素，这让数值方法的优势得到了进一步展现.此外，近年来回火研究领域还出现了一些新趋势，研究人员针对已有的数值模拟数据进行统计分析来深度研究回火现象和发掘回火机理，这也是对于边界层回火领域众多数值模拟研究结果的充分利用.

5 总结：未来边界层回火研究的方向

5.1 完善和发展边界层回火理论模型

回顾边界层回火理论模型的研究与发展历史可以发现，直到现在人们还未能完全理解边界层回火的全部机理.虽然现代的DC 模型等无量纲模型具有很高的应用价值，但是其兼容性不够好，局限于模型所针对的燃气轮机种类以及燃烧室工作条件.而兼容性广泛的FAT 模型由于发展较晚，过程不够简化，涉及的数理方程较为繁复，在工程实践中的实际可应用性较差.因此，边界层回火研究未来的发展方向之一就是发展更优秀的理论模型，其应用范围广泛，能够在避免CGM 的局限性、实现回火预测的高精度和高准确性的同时，又能保持C GM 的高可应用性，为在燃气轮机燃烧室设计中避免回火现象的发生提供理论指导.

5.2 探索发现新的回火现象和机理

过去对于回火的研究，主要针对的是气相燃烧的条件，而针对气液两相燃烧的研究数量较少.在气液燃烧条件下，燃气轮机燃烧室内的火焰发展，可能会受到液体燃料的喷射与雾化等过程的复杂作用.此外，由于在一些气液两相燃烧设备中并未明确划分预混区域，而且液体燃料的喷射、雾化、混合以及燃烧过程全部都在燃烧室中进行，针对这种情况的回火判断依据需要进一步研究.

同时，边界层回火研究对于回火机理的探索也从未停止，现代的边界层回火研究趋于将火焰界定为受限空间和非受限空间两种状态，以便更为清晰而细致地对火焰状态和回火过程进行研究.同时对于回火的研究也在引入新的变量和影响因素，比如边界层分离等.未来的边界层回火研究可以借助功能更多样化的实验装置和更强大的CFD 技术，发现更多对于回火能够产生影响的因素，来完善边界层回火机理的理论体系.

5.3 进一步发展回火研究方法

近年来，在关于边界层回火的研究中数值模拟手段发挥了越来越重要的作用，DNS 研究几乎和实验研究同时发现了CGM 的局限性.随着以LES 和DNS 方法为代表的CFD 技术不断发展，DNS 数值模拟已经成为当前边界层回火数值研究的主流理论工具，LES 方法兼顾了计算效率与模拟精度，是在工程研究和应用领域辅助理论模型进行回火预测与设计的重要方法.可以预见：在未来的边界层回火数值研究领域，DNS 会是主要的数值模拟方法.同时，近年来边界层回火研究领域也出现了一些新方法和思路，即对边界层回火DNS 数据加以二次利用，进行统计分析，进而研究回火发生时火焰的动态变化以及表面密度函数、湍流输运等参数在回火过程中的变化及其影响程度，并且与已有的研究结论相互验证.

虽然数值方法在边界层回火研究领域发挥着越来越大的作用，但是实验研究也始终是最为重要的研究方法之一，通过实验方法人们往往能够十分迅速而直观地发现各种各样的因素对于边界层回火的影响.同时，随着科技发展而带来的实验技术革新，也使得回火实验能够借助更高端的实验装置，针对更广泛的影响因素进行研究.实验研究的验证作用也是理论模型建立所不可或缺的，数值方法和实验方法可以更好地相辅相成，运用数值方法去进一步探索未被广泛研究的边界层回火的影响因素也将成为新的数值研究趋势.

另外，当前人工智能理论与方法发展速度很快，并迅速向科学和技术研究的各个领域渗透，以机器学习为代表的人工智能方法也开始逐步应用到流体力学相关研究工作中[58-59].从文献来看，目前尚未见应用机器学习等人工智能方法进行回火研究的报道，但从理论上讲，机器学习方法可以在大量相关实验及数值研究数据的基础上，基于神经网络算法，针对已有样本数据进行训练，通过强大的非线性拟合和建模能力，在建立预测模型的同时，还能考虑到影响边界层回火的所有重要因素，如当量比、压力、温度、燃烧室几何尺寸等，这是现有的理论模型和数值模拟难以做到的.从这一点来讲，以机器学习为代表的人工智能方法将是未来边界层回火研究的另外一类重要研究方法.