约束分布对混合边界薄板固有频率影响的研究★

任 帅 曹金凤 黄 伟

(青岛理工大学理学院，山东 青岛 266520)

0 引言

混合边界薄板在工程中被广泛应用，例如在建筑工程、船舶工程、微电子等领域中大量应用的边缘点焊钢板就是一种典型的混合边界薄板。由于薄板本身刚度相对较小，在激励荷载作用下容易产生振动，导致结构失效或者产生其他不利因素，混合边界条件给相关研究增加了难度，很多问题无法得到解析解。对此，国外学者开展了许多研究工作。T.Ota 和Hamada[1]使用级数法研究了简支固支结合薄板的固有频率；Helmut.F等[2]研究了不同混合边界条件下圆形薄板固有频率的变化情况和低阶模态的偏移情况；S.C. Fan和Y.K. Cheung[3]用有限条方法研究了混合边界薄板振动。国内对于混合边界薄板的研究集中于静力学问题[4-6]，在动力学方面，李广基和何志平[7]使用加权残值法解答了部分混合薄板的固有频率。而关于混合边界条件分布对于矩形薄板固有频率的影响的研究较少。

本文使用有限元软件Abaqus，对于不同边界分布和边界比例组成的简支固支混合边界条件的薄板的固有振动进行分析。为通过边界分布改变薄板的固有频率提供了参考。

1 基本方程

薄板的基本振动方程为：

(1)

其中：

其中，w为薄板上的点在t时刻的纵向位移；ρ为薄板的密度；h为薄板的厚度；p为薄板上点受到的激励力;E为弹性模量;μ为泊松比。当p(x,y,t)=0，薄板上激励力为0，这时薄板的振动是自由振动。于是薄板自由振动方程为：

(2)

简支边界条件如下：

(3)

固支边界条件为：

(4)

对于一般简单边界条件的薄板，常常使用分离变量法将薄板的位移方程分解成振型函数和时间函数的乘积方式：w(x,y,t)=W(x,y)T(t)。将满足边界条件的振型函数和时间函数代入式(2)可得到薄板的自由振动的基本振型和与其相对应的固有频率，而对于一些复杂的混合边界条件，函数W(x,y)难以求得，本文使用有限元软件Abaqus求解。

2 两种混合边界条件下的模态分析

图1和图2分别给出了薄板的两种边界条件：简支与固支，A表示A型薄板边上固支长度，B表示B型薄板上固支约束的长度，A,B两种类型薄板四边上约束一致。使用大型非线性有限元分析软件Abaqus建立模型，薄板尺寸为800 mm×800 mm×1 mm，选择单元类型为S4R，单元总数6 400，节点数6 561。薄板的材料属性为弹性模量210 000 MPa，泊松比为0.27，密度为7 780 kg/m3。模拟固支长度A分别为0 mm(四边简支)，50 mm，100 mm，150 mm，200 mm，250 mm，300 mm，350 mm，400 mm(四边固支)；B型薄板固支长度B为0 mm(四边简支)，100 mm，200 mm，300 mm，400 mm，500 mm，600 mm，700 mm，800 mm(四边固支)条件下薄板固有振动。其固有频率如表1，表2所示。

表1 A型薄板固有频率表

Hz

表2 B型薄板固有频率表 Hz

由表1，表2可以看出：随着固支长度的增加，薄板的各阶固有频率都在增加，B型薄板随着B的增加，各阶固有频率迅速增加，接近于四边固支约束；A型薄板各阶固有频率随着A增加较为平缓接近于线性增加。两种边界条件的薄板在固支长度相同时，B型较A型薄板的固有频率在每一阶上都偏大，这种情况在固支边界长度较小时更为明显，例如在A=100 mm，B=50 mm时固支长度总量在两种薄板上长度一致,而A板的基频是B板基频的1.483倍，但高阶频率相差较小；第8阶时，A板固有频率是B板固有频率1.017倍，这种现象随着固支约束提高而下降。对于一条边固支长度为700 mm时(A=700 mm，B=350 mm)，B板基频是A板基频的1.0312倍；第8阶时，B板固有频率是A板的1.008倍。可以认为：随着固支长度增加，约束分布对于薄板的固有频率影响变小。

3 几种混合边界条件薄板固有频率分析

以B型边界条件薄板为基础，研究了部分约束失效或改变时薄板的固有频率变化。如图3～图6所示，C型薄板固支约束分布在三边上；D型薄板的固支约束分布在两个对边上；E型薄板固支约束分布在两个邻边上；F型薄板只在一边上布置固支约束。四类薄板的固支约束都分布于边的中间，除固支约束以外其余边的边界条件都是简支约束。C，D，E，F分别为C型D型E型F型边上固支约束的长度。薄板尺寸与材料属性与第2章一致。使用Abaqus软件分析四种薄板固有频率，结果见表3～表6。

表3 C型薄板固有频率表

C/mm第1阶第2阶第3阶第4阶第5阶第6阶第7阶第8阶07．754519．39519．39531．0338．82738．82750．45350．45310010．6321．45323．24631．59840．26845．23751．79351．89820011．45722．624．94433．20341．46147．46652．56653．13530011．99623．63626．35435．47943．17248．97653．94955．29840012．30424．35627．29637．64344．70150．11956．35958．52350012．44624．72927．7638．98845．47250．92158．53161．30560012．49524．86527．91739．5145．73151．24959．51662．49670012．50524．89427．94739．61845．78451．31359．73162．73480012．50624．89627．94939．62445．78751．31759．74462．747

表4 D型薄板固有频率表

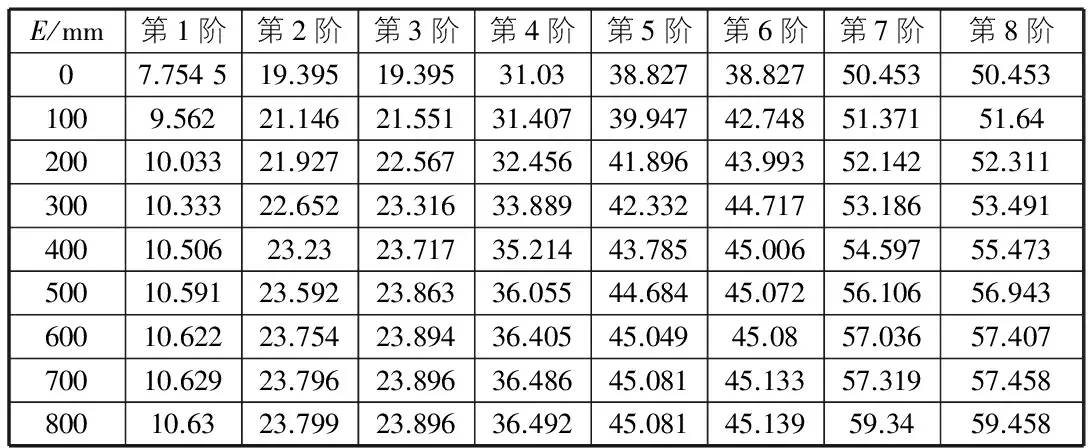
表5 E型薄板固有频率表

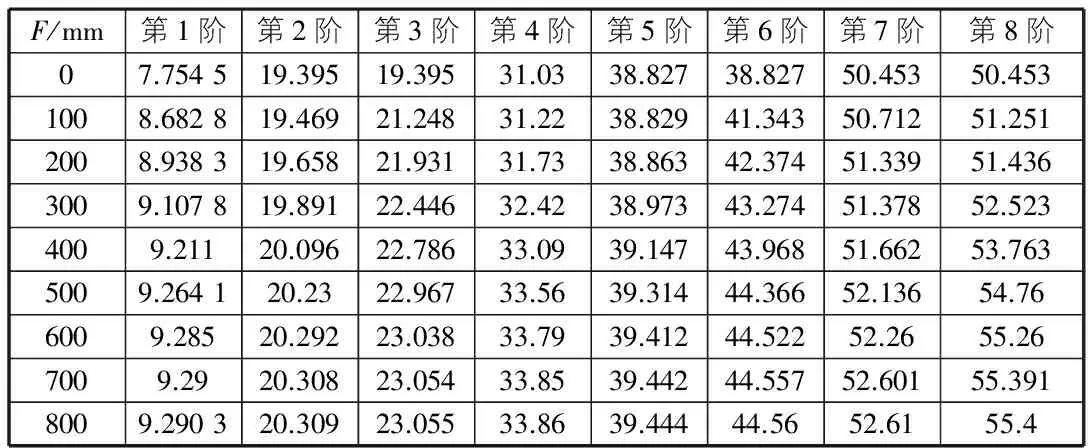
表6 F型薄板固有频率表

由表3～表6可见，几种薄板的各阶固有频率随着固支长度增加而迅速增加，其趋势与B型薄板相近，迅速接近于全边固支。基频呈现出fB>fC>fD>fE>fF。值得注意的是：D,E在其边上的固支边界长度相同时，其总的固支边界长度是一致的，而D型边界薄板的基频大于E型，第二阶fF>fE，第三阶时fE>fF，其固有频率大小关系交替变化。

在固支长度一定时，薄板前几阶固有频率存在fB>fC>fD(fE)>fF>fA,而高阶频率差值较不明显，除了B稍大于其他类型的薄板外，其他类型薄板固有频率均相近，可以认为边界条件分布对于高阶固有频率影响较小。

4 结语

1)对于混合边界条件矩形薄板，其固有频率可以通过调整边界约束条件比例来改变。对于简支/固支混合边界条件的薄板，固支边界占总的边界长度的比例越大其固有频率越高，反之固有频率越低。

2)简支/固支混合边界条件薄板中，将固支边界分布于板边的中间要比固支边界分布于板的角位置增加固有频率的效率会更好，尤其在增加基频上效果最好，但对于高阶振动这种现象并不明显，即对于高阶振动，边界条件的布置方式对其影响较小。通过调节边界分布方式来调解薄板的基频效果较好，对于调节高阶固有频率的效果较差。

3)对于简支/固支混合边界条件薄板，固支边界在总的边界长度中所占比例越大，分布方式对于薄板固有频率的影响越小。

[1] T. OTA,M.HAMADA. Fundamental frequencies of simply supported but partially clamped squareplates[J].Bulletin of Japan Society of Mechanical Engineering，1963(6)：397-403.

[2] Bauer, Helmut,F. Werner Eidel.Approximate natural frequencies of circular plates with mixed boundary conditions [D].Universitaet der bundeswehr muenchenneubiberg,2004.

[3] S. C. FAN,Y. K. CHEUNG. Flexuralfree vibrations of rectangular plates with complex supported conditions[J].Journal of Sound and Vibration,1984(93)：81-94.

[4] 陈立志,付宝连.简支与固定混合边界条件矩形薄板的弯曲[J].东北重型机械学院学报,1993(1):67-80.

[5] 史宝军,鹿晓阳,许焕然.一个简明有效的四边形杂交/混合薄板弯曲单元[J].工程力学,2000(2):102-110.

[6] 李建华,曲庆璋.两对边自由另两边自由与固定混合支承矩形板的弯曲[J].强度与环境,2001(1):32-37.

[7] 梁广基,贺志平.混合边界矩形薄板的自由振动[J].力学与实践,1991(5):17-20.