基于拓展峭度的电缆缺陷高分辨率定位方法

高春林，刘国锋，胡意茹，张安安

(1.西南石油大学，成都 610500； 2.中海油研究总院有限责任公司，北京 100028)

0 引 言

随着电网的复杂化以及愈加高度的关联性，电力电缆应用日益广泛，扮演着越发关键的角色。一旦电缆发生故障将影响电网及关联用电设备的安稳运行并可能导致严重经济损失。老化是导致电缆故障发生的重要原因[1-2],而在故障初期通常表现为微弱缺陷，为能尽早发现电缆隐患，检测并掌握缺陷位置至关重要。

电缆故障定位技术目前主要可分为时域反射分析法(TDR)和频域反射分析法(FDR)。TDR发展较早也最为成熟，其通过向待测电缆发射脉冲信号，测量脉冲信号遇到故障产生的反射信号到达发射端的时间实现电缆故障的定位[3-5]。由于需要捕捉反射信号，当电缆故障较为微弱时较低的阻抗不匹配程度和信号传输过程中的衰减将导致反射信号不够明显从而难以实现故障准确定位，故TDR难以定位早期微弱的故障[6-7]。并且信号往返时间的测量误差也会在一定程度降低定位精确性。所以TDR难以满足现代检测手段准确预知、监测故障的发展趋势。

频域反射分析法多是通过向待测电缆发射正弦扫频信号采集电缆输入阻抗谱检测、定位电缆故障。当电缆发生缺陷时会引起电缆输入阻抗谱发生改变，通过分析电缆输入阻抗谱即可确定缺陷位置。电缆输入阻抗谱技术最早于21世纪初提出并用于核电站电缆诊断，电缆阻抗频谱包含了大量电缆运行特性，文献[8-10]通过LIRA算法实现对电缆健康状况的诊断以及缺陷定位，但其定位曲线未制作缺陷的地方有“误判点”出现，易混淆对缺陷处的判断。近几年通过傅里叶变换分析电缆阻抗频谱也实现了电缆缺陷定位，文献[11]使用快速傅里叶变换实现了对电缆缺陷的定位,在此基础上，文献[12-13]探讨了不同辐射强度、温度对实验的影响，文献[14]研究了电缆结构对实验的影响，文献[15]研究了绝缘材质对实验的影响。但基于输入阻抗谱得到的定位曲线两端通常有高于缺陷处幅值的“屏蔽带”出现，将会影响对缺陷处的判断，并且也存在混淆缺陷位置判断的“误判点”。在数据处理时加窗函数的方法能够在一定程度提高缺陷处峰值的幅值，但是这仍然不足以完全回避易“误判点”对定位曲线的影响。并且考虑到缺陷幅值与故障的严重程度成正比，所以对于定位、评估更加微弱的缺陷，更高缺陷处幅值是至关重要的一环。

文章通过分析电缆输入阻抗谱特性及其变化的根本原因，提出一种基于拓展峭度与传输系数谱结合的高分辨率高精度缺陷定位方法，即定位曲线中故障处与非故障处有直观、明显的区别，甚至能通过肉眼观测，且定位曲线中故障位置与实际故障位置相差很小，其体现为更小的定位误差。通过对定位曲线提取峭度特征量，从峭度的角度对定位曲线进行定量分析，再将峭度特征曲线延展为拓展峭度以适配原有数据的数量，最后与原始定位曲线相乘，最终实现高精度、高分辨率缺陷定位，成功降低易误判点的干扰，与现有频域反射分析法的定位曲线相比几乎不存在误判点(误判点与缺陷处幅值最高相差3个数量级)，并且在扫频信号带宽较宽的情况下能一定程度提高定位精度，拓展了频域反射分析法实现精准定位的适用范围。

1 传输线理论

在高频下，一般是电长度l/λ大于0.1时，传输线通常作为分布参数电路来考虑[16-17]，其等效图如图1。

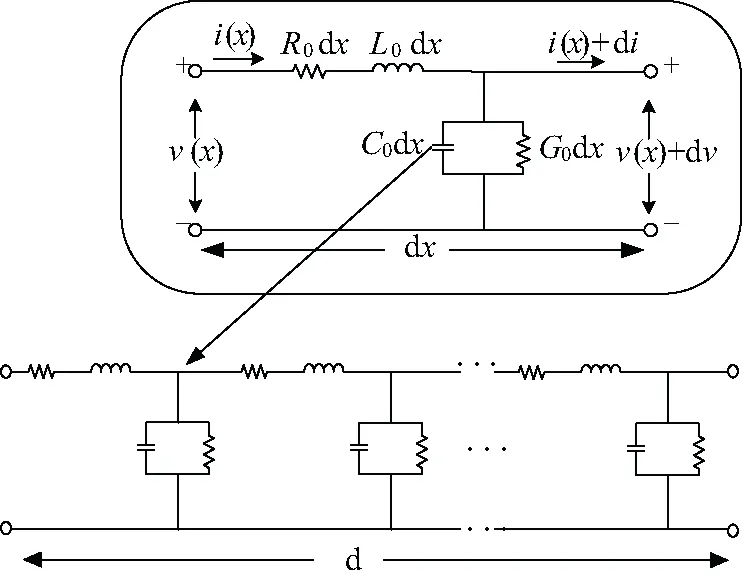
图1 分布参数电路Fig.1 Distributed parameter circuit

图1中R0、L0、C0、G0分别代表在分布参数情况下传输线的单位电阻、单位电感、单位电容、单位电导。在扫频下，可近似为文献[18]。

(1)

(2)

单位电容C0与单位电导G0不直接受频率影响，主要与电缆本身特性相关[19][20]，可按照静电场方式进行计算：

(3)

(4)

式中ω为信号发生器角频率;μ0为真空磁导率(铜导体磁导率与真空磁导率相同)；σc、σs为电缆线芯及屏蔽层电导率；ε为电介质介电常数；σ为电介质电导率；rc、rs分别为电缆线芯与屏蔽层内半径。在分布参数情况下，通过求解波动方程可得到输入阻抗Zin、传输系数γ如下[16]：

(5)

(6)

(7)

(8)

式中d为电缆长度；γ为传输系数；α为衰减系数；β为相位系数。输入信号为扫频信号时，传输系数、输入阻抗具有频率依附性，均会随着频率变化而变化。

2 基于传输系数谱电缆缺陷定位方法

2.1 传输系数谱定位原理

输入阻抗谱能够在一定程度上反应电缆状态变化，电缆发生缺陷时输入阻抗谱将会改变，如图2所示。

图2 输入阻抗谱Fig.2 Input impedance spectrum

图中无标记曲线为缺陷电缆输入阻抗谱，带“+”号标记曲线为发生老化后的电缆输入阻抗谱，对比可看出，老化后输入阻抗谱发生了变化。而通过式(5)可知，主要影响输入阻抗谱性质的是因子e-2γl， 进一步分析，其性质反应在传输系数γ中。传输系数与加载在电缆上的电压无关，仅与电缆的几何尺寸、结构、材质以及信号频率有关。所以这使得利用测量传输系数进行电缆故障检测和定位成为了可能。

综上可知，输入阻抗反映电缆状态的实质是由于传输系数对电缆自身特性的表征。在高频下传输系数谱将直接表征电缆状态，故直接分析电缆传输系数将对电缆运行状况有更直观的掌握。

2.2 基于s参数的采集方法

文献[21]通过对反射系数谱的测量实现了对因子e-2γl的提取，并实现电缆故障定位。通常情况下电缆传输系数难以测量，但将传输线视为一个二端口网络，利用s参数可以实现对传输系数的精准采集。s参数即散射参数，是建立在入射波、反射波关系下的一种网络参数，适用于分布参数电路，可描述电阻在高频信号激励下的射频特性。由“三点式测量”方法可以求得电缆的传输系数与s参数的关系：

S21=e-γl

(9)

图3为健康电缆与老化缺陷电缆的传输系数谱对比图，从图3中可看出，在完好状态和老化缺陷下的电缆传输系数谱出现了明显的差异。这种递增的差异性表明传输系数谱可以敏锐察觉电缆状态的变化。

图3 传输系数谱Fig.3 Propagation coefficient spectrum

2.3 数据处理方法

由于传输系数谱对于电缆自身特性改变非常敏感，通过一定数据处理方法将电缆传输系数谱从“频率关系”转换为“空间关系”可以对电缆缺陷进行有效识别及定位[11]。常见的转换函数是傅里叶变换或傅里叶逆变换，在数字信号处理中一般选择离散傅里叶变换(DFT)或离散傅里叶逆变换(IDFT)。DFT可将一个信号从时域变换为频域，而IDFT可将信号从频域转变为时域。因此DFT或IDFT可将包含电缆缺陷信息的传输系数谱转换“距离谱”。

图4为基于拓展峭度与输入阻抗谱结合的电缆缺陷定位方法流程图。

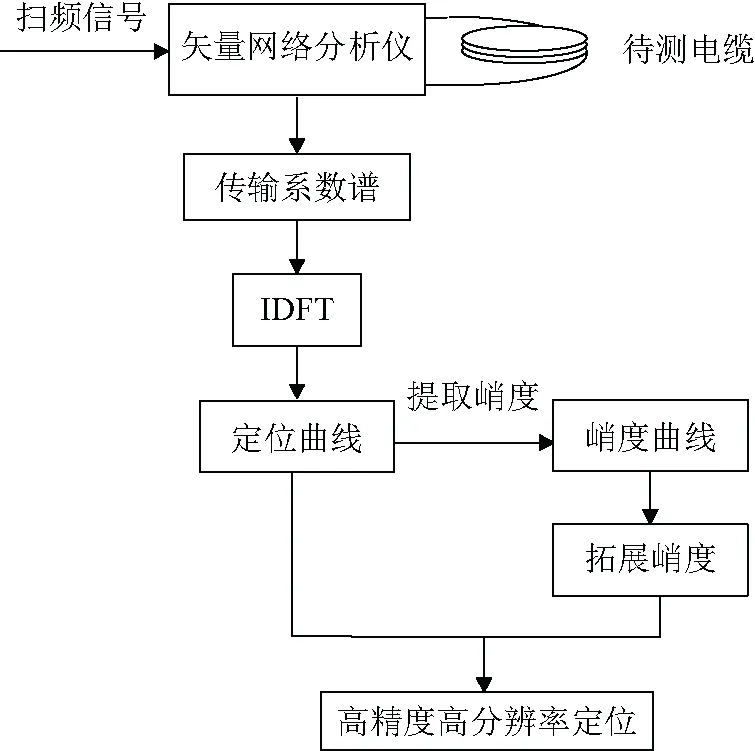
图4 基于传输系数谱定位方法流程图Fig.4 Flow chart of localization method based on propagation coefficient spectrum

3 实验结果与分析

利用矢量网络分析仪,采用双端口测量方式通过SLOT的直通件校准可测得S21参数进而获得电缆传输系数谱。为了验证文章所提出方法，在14.92 m电缆上进行试验，通过隔离水浴法以80 ℃、100 h的恒温恒时方式在11.20 m处模拟电缆局部老化缺陷，缺陷长0.01 m。

为探究带宽对最终定位结果的影响，对起始频率为45 MHz，带宽分别为300 MHz、500 MHz、800 MHz、1 GHz的传输系数谱进行实验。通过IDFT将传输系数谱从“频域”转换到“空间域”，得到电缆老化缺陷定位曲线如图5(a),同时我们将图5(a)按频率沿z轴展开，得到图5(b)。

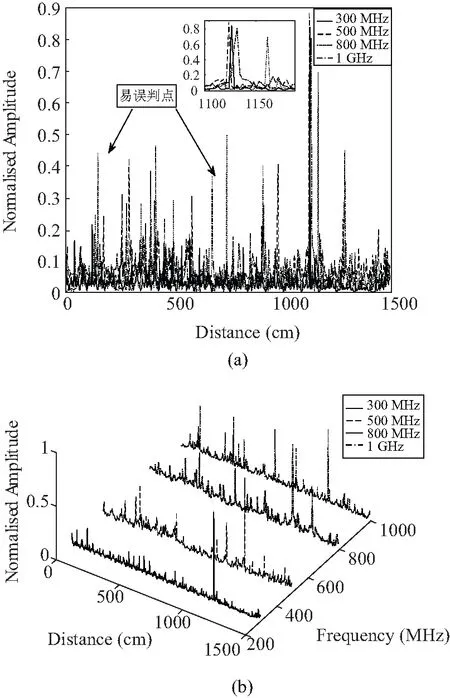
图5 电缆老化缺陷定位曲线Fig.5 Location curve for cable aging defect

图5(a)中分别是带宽300 MHz、500 MHz、800 MHz、1 GHz时的定位曲线，四种带宽下的“畸变峰值点”均位于1 120 cm处附近，且均未出现“屏蔽带”。对比不同带宽下缺陷位置可发现，300 MHz带宽时的缺陷定位曲线“畸变峰值点”位于1 124.5 cm处，定位误差通过式10约为0.3%，同时可观察到此时曲线“毛刺”较少，500 MHz带宽缺陷定位图“畸变峰值点”位于1 121.4 cm处，定位误差约为0.1%，当带宽达到800 MHz时，“畸变峰值点”位于1 130 cm附近，其定位误差约0.6%，达到1 GHz带宽时，“畸变峰值点”位于1 160 cm附近，与实际故障点位置已有较为明显的偏差，定位误差高达2.8%。

(10)

式中e为定位误差;dc为定位图谱中缺陷处位置;dm为实际制作缺陷位置;d为电缆长度。

3.1 频率对测试及定位的影响

为说明定位曲线中缺陷处幅值“畸变”程度，对得到的定位曲线进行峭度分析。将长为n的定位曲线f(γ,n)均分为j等分的小窗，每个小窗长M，任一段曲线f(γ,ni)峭度数学表达式为：

(11)

式中K为峭度值；μx为曲线均值；σx为曲线方差。峭度能够给描述曲线中的“冲激成分”[22]，可应用于电缆局放信号的识别[23]。零峭度定义为峭度K=3时的分布曲线，当其分散程度减小，峭度值将增加，即曲线分布越“陡峭”其峭度值越大。基于此，通过峭度曲线f(K,n)的幅值大小分析定位曲线的分辨率以及“易误判点”的数量和幅值并确定上限频率阈值。

提取峭度特征的图形如图6所示，从图中可知，随着带宽从300 MHz上升到800 MHz，“畸变峰值点”处的峭度值随之增加，即定位曲线分辨率提高。但当到带宽达到1 GHz时，“畸变峰值点”的峭度值降低至8 000左右，将不利于我们对缺陷点的准确判断。对比四种带宽下的“易误判点”可看出，随着带宽增加，“易误判点”的幅值以及数量都呈现上升趋势，当带宽到达1 GHz时，“易误判点”的幅值与“畸变峰值点”的幅值已相当接近达到了同一数量级内，将会影响我们对缺陷点的判断，故有必要设定测试信号上限频率阈值进行限制。

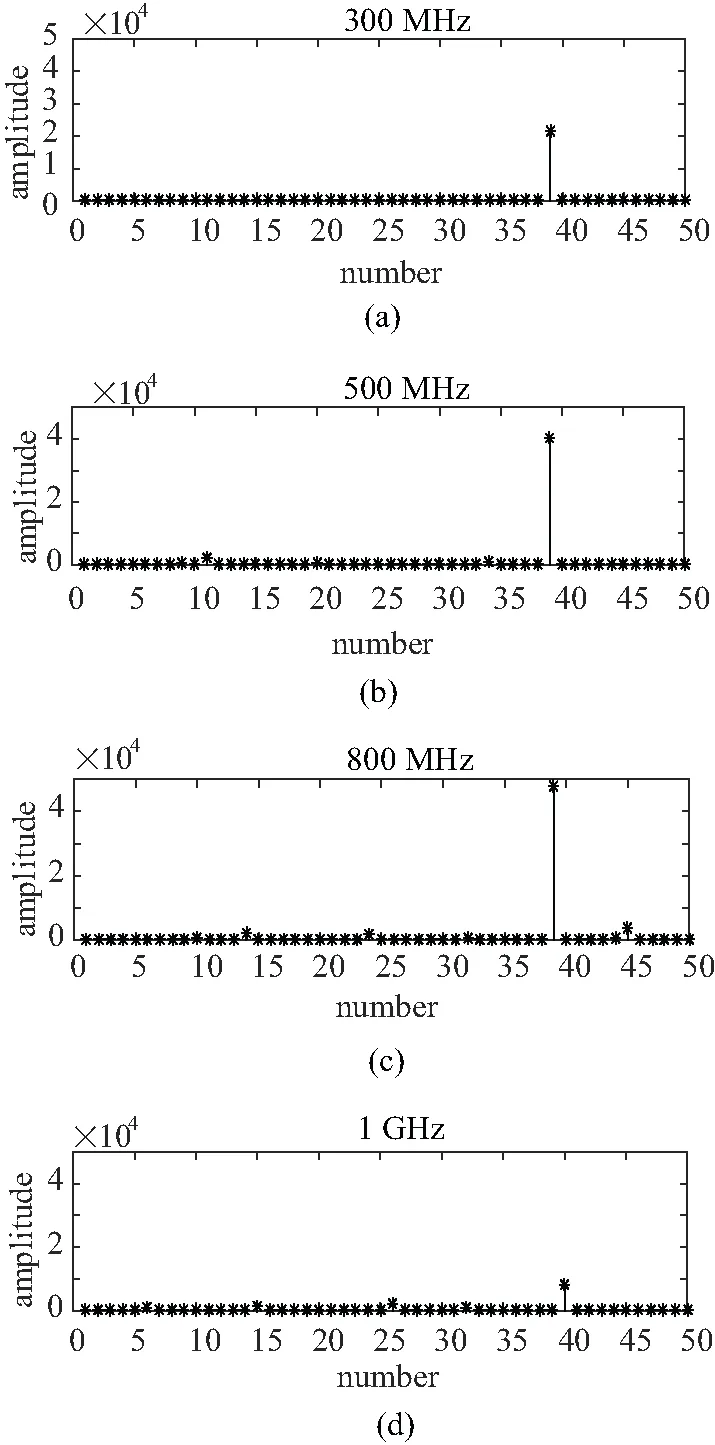
图6 定位曲线峭度对比图Fig.6 Comparison diagram of localization curve kurtosis

为比较带宽对定位结果的影响，我们将定位曲线信息以及峭度图以表格形式汇总，如表1。通过表1和定位曲线图5(a)可知，随着带宽从300 MHz增加至500 MHz，缺陷定位结果的精度随之提高，定位误差从0.3%下降到0.1%，而当带宽继续增加，由于接头处的影响以及噪声的影响导致定位误差开始上升。同时结合表 与图5(b)可看出，当带宽从300 MHz增加至800 MHz缺陷处峭度值随着带宽增加而增加(21 600增加至47 850)，但将更容易出现“易误判点”体现为非缺陷处的尖峰值增加。当然这些“易误判点”不会直接影响定位精度，但其幅值较高时易混淆对缺陷位置的准确判断。

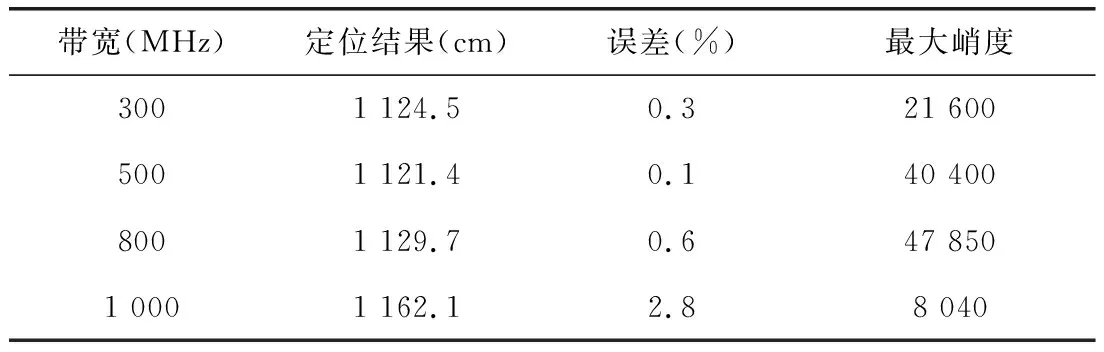
表1 定位曲线对比表Tab.1 Comparison of localization curves

当扫频信号上限频率控制在600 MHz内时“易误判点”虽然存在但其幅值依然远低于缺陷处幅值，可通过幅值大小与缺陷点区分。当扫频带宽超过限制带宽时，由于扫频信号频率过高导致接头处引入的额外电容对电缆及传输系数谱产生较为明显的影响，定位精度反而呈下降趋势，同时“易误判点”幅值上升，“畸变峰值点”幅值下降，致使“畸变峰值点”与“易误判点”更易混淆。

综上可知，对同一起始频率，增加上限频率会使缺陷更明显体现，但是当频率上限或带宽过高将导致电缆接头引入的额外电容等其他因素对传输系数谱的测试以及定位造成影响，所以我们将本方法中的扫频信号上限控制在600 MHz。当上限频率低于阈值时，增加带宽在一定程度上能够提升定位精度与定位分辨率，但可能会导致“易误判点”的出现，适当降低扫频信号带宽可在保证定位精度的情况下减少这种情况发生，可根据缺陷类型、缺陷严重程度以及电缆长度进行合理取舍。同时在限制频率以内，通过传输系数谱得到的定位曲线可保证小于0.5%以内甚至仅0.1%的定位误差，优于现在大多数的时频域定位方法。

3.2 基于拓展峭度的提升定位曲线空间分辨率方法

由图6以及峭度定义可知，峭度能够衡量曲线凸起的程度，并在一定程度上反映易误判点大小，同时由于在计算峭度时将原始曲线分割为了若干个子窗来计算并且使用了方差与均值等参量，使峭度图可以忽略定位曲线中的一些凸起，这将使得易误判点减少。所以若将峭度视为一个权重再与定位图结合则可以“过滤”易误判点，从而提升定位效果。

由于在计算峭度时选取了10个点作为一个小窗，则在与定位函数结合前需要将窗函数拓展，形成拓展峭度窗函数，使峭度点数与定位曲线点数相同，以适配后续处理，如图7所示。

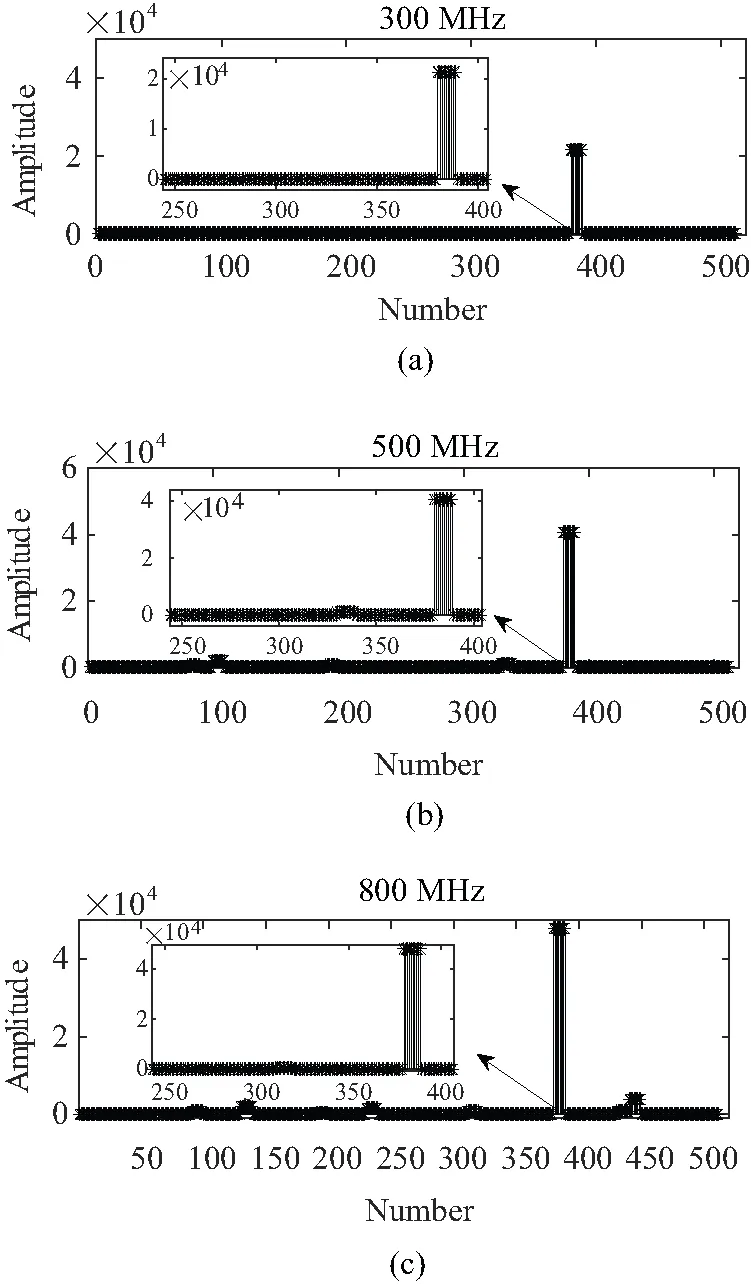
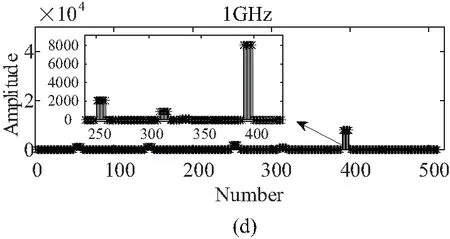
图7 拓展峭度Fig.7 Expanded kurtosis

从图7可以看出，将每一点峭度值拓展为10点，以此形成拓展峭度窗函数，而峭度值并未改变，依然反映了定位曲线的缺陷表达能力以及蕴含易误判点的信息。将拓展峭度窗函数与定位曲线相乘，可以得到“滤波”后的定位曲线，如图8所示。

图8 基于拓展峭度定位曲线Fig.8 Localization curve based on expanded kurtosis

通过扩展峭度形成窗函数，再与定位曲线相乘得到的滤波后定位曲线几乎不含有任何误判点、易误判点以及定位盲区。这是因为将拓展峭度作为权重与定位曲线相乘的步骤进一步增大了缺陷处幅值与易误判点等其他处幅值的差异。

图9为处理前后定位曲线对比。原始定位曲线的易误判点处幅值一般为缺陷处幅值的0.3倍以上，最大超过了0.5倍，此时易误判点幅值极为接近缺陷处的幅值，易对准确判断缺陷造成影响，而观察处理后定位曲线发现，随着频率增加本应出现的由测试原因引起的易误判点幅值增加的现象几乎完全消失，从图9中的放大处可以看到滤波前呈易误判点位置的幅值仅有20不到，而缺陷处幅值在四种不同频率下分别达到了：18 900/19 100/17 500/1 800，如表1 所示，与其他凸起处幅值相差百倍甚至千倍，所以此时易误判点对缺陷定位的影响大大下降，甚至可以完全忽略。

图9 拓展峭度处理对比图Fig.9 Comparisonof localization curve based on extended kurtosis processing

将不同频率沿z轴展开可得图10，从图10中可以看出随着频率增加本应出现的由测试原因引起的易误判点幅值增加的现象几乎完全消失，仅有缺陷处的幅值呈现出一定差异。

图10 不同频率峭度处理对比图Fig.10 Comparison of processed localization curve in different frequency

同时与800 MHz及其以前的带宽不同的是，当扫频信号频率达到1 GHz以上时幅值骤降至1 200左右，这是因为1 GHz的峭度值比其他频率的峭度值更低，故在相乘后幅值相比其他频率更低。但其根本原因仍是因为在1 GHz时由于测量或校准原因导致传输系数谱出现了额外的抖动以及噪声的影响，最终导致在有无缺陷的差异出现异常变化，最终导致缺陷反映能力降低。

但值得一提的是，对比1 GHz处理前后的图像，可以发现除了可以降低易误判点对定位曲线的影响，其精度也有了显著的提升，从之前在1 162.1 cm处的峰值变为了在1 117.1 cm附近，其定位精度提升了2.6%，将图中定位信息汇于表2所示。

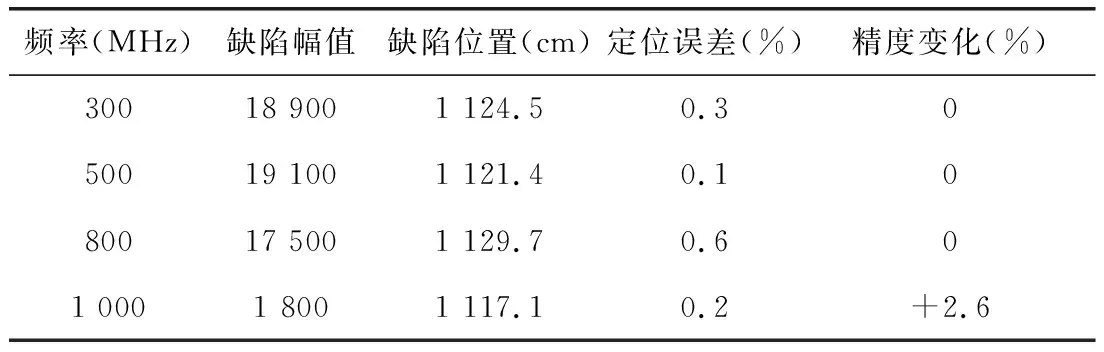
表2 处理后定位信息Tab.2 Locating information after processing

现有基于频域反射分析法的技术中，文献[21]中定位误差可以保证小于0.6%，文献[24]中定位误差约为1%, 文献[25]中定位误差约为0.8%, 而文献[26]中定位误差约为1.5%。对比可知，文中所提方法在保证一定带宽的情况下优于现有的方法，同时能够提高定位图谱分辨率，使得故障位置相比其他方法更容易分辨，不受易误判点干扰。

综上所述，由表可知，300 MHz、500 MHz、800 MHz的定位曲线与拓展峭度窗函数相乘后可在保证定位精度不变的情况下大幅降低易误判点对缺陷判别的影响。同时对于较高频扫频信号通过拓展峭度作为权重相乘，不经能够在降低易误判点影响，还可以在一定程度上能够提高定位精度。

4 结束语

文章提出了一种基于拓展峭度的频域反射分析法高精度高分辨率定位方法，通过对定位曲线提取峭度特征量再延展为拓展峭度并与原始定位曲线结合得到新定位曲线，能够大幅降低定位曲线中的易误判点，提高了定位分辨率。同时在不同带宽下进行了实验，研究了带宽对传输系数谱定位的影响。在不同带宽下的实验结果表明基于拓展峭度的定位方法在有效降低误判点时不会改变定位精度，同时对于1 GHz的更高频扫频信号，所提方法不仅能够提升定位曲线分辨率，还可以在一定程度上提高定位精度，这有助于将频域反射分析法高分辨率、准确定位缺陷的应用拓展到GHz以上的带宽数量级。