市场环境下共享汽车电池仓库能量管理策略研究

林洋佳，杨军，Ghamgeen Izat Rashed，詹祥澎，吴赋章，龙雪梅

(武汉大学 电气与自动化学院， 武汉 430072)

0 引 言

随着环境问题和交通压力的日益突出，电动汽车作为一种绿色出行工具，替代燃油汽车成为未来主要交通工具已经成为时代发展的趋势[1]。与此同时，共享出行的应用将极大地改善城市交通拥堵和基础设施紧缺的现状，在满足出行需求的同时可以免除维修保养、停车等费用，是未来交通出行的热门领域[2]。

文献[3]推广电池租赁等车电分离的消费方式，鼓励研制充换电结合的汽车产品，以促进换电模式的发展。换电模式本身具有流程快捷、电池可调度性强等特点[4]，通过共享电动汽车运营商的统一管理，无须担心电池型号、接口等问题，在共享运营中选择换电模式具有良好的发展前景。

电动私家车由于行驶特性随机性强，其电能补充形式受用户意愿的影响较大[5]，因而其换电规律的掌握尚不完全，加之型号、接口标准尚未统一，对换电模式的推广造成了极大的阻碍。相比之下，基于换电的共享电动汽车可以在满足随机性极强的私家车出行需求的同时，通过将不同的出行需求在时间上组合后，又因其大规模运营的规模效应，换电需求的随机性大幅减弱。故而对共享汽车电池仓库的容量状态和配送需求的预测准确性相对较高,又因其统一的运营和管理，为其参与电力市场提供了很大的便利。因此，有必要对基于换电的共享电动汽车运营进行研究，分析其电池仓库的能量管理问题，为其参与需求侧响应提供理论支持。

现有的共享电动汽车研究大多从车辆调度、网点规划、需求预测等角度入手。文献[6-7]对站点间车辆失衡的问题进行研究，基于成本最小化设计了车辆调度方法，文献[8]通过激励用户参与车辆调配的积极性来降低车辆调度的成本，文献[9]将车辆作为移动边缘计算的服务器收集对共享电动汽车的出行需求，从而对服务网点选址进行优化，而文献[10]考虑资金约束提出了满足服务范围内充电需求的充电站选址定容方法，文献[11]则将选址和调度进行联合优化以求更好地解决网点布局以及车辆供需平衡的问题，文献[12]考虑时空特征变量的交互影响，对共享电动汽车的充电负荷进行预测。文献[13]研究了共享电动汽车的充电管理问题，设计了一个智能的充电框架降低了电价高峰时段的充电负荷，同时证明了电动汽车负荷可以较好地消纳光伏发电，为降低充电成本提供了思路。总体而言，现有文献大多对共享电动汽车的整车充电模式进行研究，鲜有文献对换电模式展开分析。此外，对换电模式的研究也主要集中在换电站规划和电池调度上，重点考虑了电池的物流配送问题[14]、换电站的选址定容[15]以及换电站间的电池调配[16]，却忽略了换电所需的电池仓库相比于电动汽车聚合商，对调度指令的响应程度更高，有更大的优势可以通过参与电力市场竞价的方式进行能量管理，改变自身的效益水平。

目前针对基于换电模式下的共享汽车电池仓库的研究十分缺乏，对电池仓库的充放电管理和参与电力市场竞价更是鲜少涉及。因此，文章提出了电池仓库能量管理的双层规划模型。上层以电池仓库成本最小化为目标对电池充放电功率进行优化，下层对电池仓库参与日前电力市场的出清过程进行建模。利用KKT条件和强对偶理论将模型转换成混合整数线性规划问题，调用求解器进行优化求解。最后，通过算例仿真验证了文章所提模型的可行性和有效性。

1 共享电池仓库运营模式分析

基于换电模式的共享电动汽车采用集中充电统一配送的运营模式，电动汽车在使用完毕返回服务网点后，根据电池电量情况进行电池更换和回收操作，更换下来的电池运送回电池仓库，进行统一的充放电调度，待达到电量阈值后根据用户需求配送至相应的共享服务网点，其电池流动和信息交互情况如图1所示。

图1 共享电动汽车电池配送示意图Fig.1 Schematic diagram of shared electric vehicle battery delivery

共享电池仓库中聚集了较大规模的电池，加之其灵活的充放电调度方式，为其提供了参与需求侧响应的机会。电池仓库可以根据市场出清电价，合理安排电池能量管理策略。由于出清电价在事前是未知的，文中将电池仓库作为电力市场的参与者，与发电商一起提交报价，从而模拟市场出清的过程，形成出清电价。电池仓库根据共享用户的电池需求，参考日前市场中其余参与商的报价，确定自己的报价策略。其过程如下：

(1)电池仓库对共享运营情况进行预估，主要包括运回电池仓库的电池电量情况、共享电动汽车的电池需求等；

(2)电池仓库基于运营需求，同时估测参与竞价的对手的报价，制定自身的竞价策略，向电力市场交易中心提交报价；

(3)交易中心根据各参与者提交的报价，基于电力供需平衡以及社会效益最大化的原则进行市场出清，可获得电池仓库的充放电电量以及出清电价；

(4)电池仓库基于获得的充放电电量和共享运营的电池需求，对每个时刻各电池的充放电功率进行优化管理。

2 共享电池仓库能量管理模型

针对上述市场出清过程，文中构建了共享电池仓库最优报价和能量管理的双层规划模型，如图2所示。上层以电池仓库的效益最优为目标，对电池的充放电功率进行优化，下层以社会效益最大化为目标进行市场出清，从而决定各参与者获得的电量。上层模型向下层模型提供电池仓库的竞价策略，故而下层模型中所有参与者的报价均为已知，可以完成市场出清。下层模型则可以为上层模型提供统一出清的电价和电池仓库的中标功率，从而以此为基准调整仓库内可参与调度的电池充放电功率，上下两层模型交互影响。

图2 共享电池仓库能量管理双层规划模型Fig.2 Bi-level programming model for energy management in shared battery warehouse

2.1 上层电池仓库模型

电池的使用寿命受充放电循环次数的影响很大，频繁的充放电会给电池造成很大的危害，在考虑电池仓库的使用成本时包含了电池损耗成本和用电成本两部分，上层模型的目标函数表达式如下:

(1)

文中选取经典损耗模型计算电池损耗成本，其表达式如下：

(2)

式中CBLd为深度充放电模式下每单位电能导致的电池损耗成本；CB为电池的购买成本；LC为标称的电池充放电循环次数；EB为所选用的电池容量；d为与标称循环次数对应的电池放电深度。

在经典损耗模型中，电池循环寿命仅与放电深度有关，当放电深度减小时，电池损耗成本会有明显下降。电池仓库通过对电池的统一管理使得电池的使用价值最大化，大多数情况下处于浅度充放电循环模式，可通过下式进行简单估计[17]：

CBL=kCBLd

(3)

式中k为浅度充放电模式下单位电能的损耗成本占深度充放电模式的比例。

电池仓库的约束条件如下：

(1)电池可调度状态约束

(4)

xt,n∈{0,1}

(5)

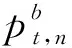
(2)电池充放电功率约束

(6)

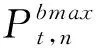
(3)电池电量等式约束

(7)

式中St,n为第n块电池在t时刻荷电状态(SOC, State of Charge)；η为电池充放电效率。

(4)电量安全约束

Smin≤St,n≤Smax

(8)

式中Smax和Smin分别是电池SOC的上下限。

(5)电池使用需求约束

Stl,n≥Sb

(9)

式中Sb为电池出库所需达到的最低SOC要求，Stl,n为tl时刻(即第n块电池进入预备配送状态，不再参与充放电调度的时刻)电池的SOC。

(6)充放电设备数量约束

(10)

式中N为电池仓库的充放电设备的数量；Psmax和Psmin分别为充放电设备所允许的充放电功率的上下限。

2.2 下层市场出清模型

市场出清模型以社会效益最大化为目标函数，即市场总购电费用最低。假设系统运行过程中没有出现输电阻塞，满足电网安全运行的条件，主要考虑发电商与电池仓库的竞价过程，不考虑其他市场参与主体。因而约束条件中包括各时段的功率平衡约束和发电商的功率上下限约束，表达式的冒号之后是各约束条件对应的拉格朗日乘子。

(11)

(12)

(13)

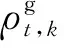
3 双层优化模型的求解

将双层优化模型转换为单层模型是解决双层优化问题的常见方法。由于下层优化模型的目标函数是凸函数，由约束条件可知其可行域是凸集，因而下层是凸优化问题，可通过KKT条件将双层模型转化为单层模型。再利用强对偶理论和大M法将模型线性化，即可直接利用求解器获得优化结果。

3.1 市场出清模型的KKT条件转化

市场出清模型的拉格朗日函数为：

(14)

通过KKT条件将下层模型转换为：

(15)

(16)

(17)

(18)

(19)

其中，式(15)～式(16)为拉格朗日函数对下层模型各个变量的偏导所构成的等式约束；式(17)为原下层模型的等式约束；式(18)～式(19)为原下层模型的不等式约束与对应的对偶变量构成互补条件。

3.2 模型线性化

(20)

(21)

(22)

通过以上步骤，原双层优化模型已经转换为混合整数线性规划模型，可调用CPLEX商用求解器直接进行求解。

4 仿真分析

4.1 算例参数设置

文章假设某区域共享电动汽车运营商的车辆规模为2 500辆，以保证共享运营为基本需求，不考虑为参与电网辅助服务等增值服务而调整电池规模，文中设定的车辆和电池的比例为1:2，基于美国NHTS2017的出行统计数据，可预测得到各时段的电池换电需求，如图3所示。考虑到共享电动汽车在凌晨的使用需求和换电需求都很小，而凌晨的电价相对较低，充电过程多在此期间完成，因而选择早上6点～次日6点作为仿真时段，时间间隔为1 h。

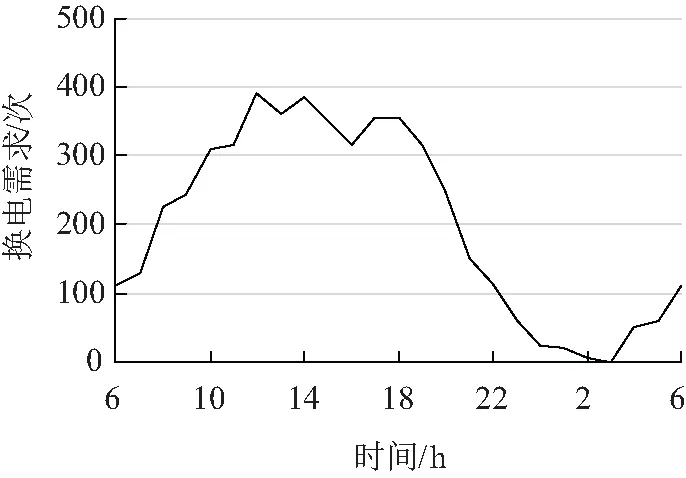
图3 电池换电需求Fig.3 Requirements for battery-swapping

假设有3个常规机组的发电商与电池仓库一同参与日前电力市场竞价，各发电机组的出力区间为0～40 MW，参考PJM电力市场公布的报价数据，计算各个时段的平均报价作为该发电商的预测报价，如图4所示[19]。假设该区域内有一个风电场，风电在电力市场中为全额收购，无需参与竞价，其风电出力数据参考文献[20]。和基本负荷曲线共同绘制在图5中，其余参数设置见表1。

图4 发电商报价曲线Fig.4 Quoting curve of generators

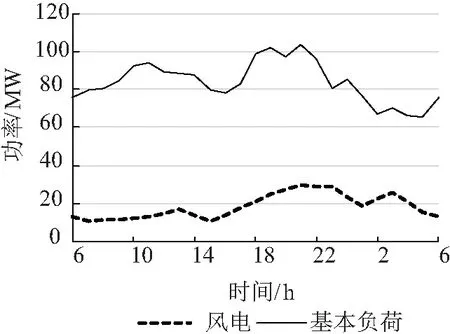
图5 风电和基本负荷功率曲线Fig.5 Power curves for wind and base load

表1 算例参数设置Tab.1 Parameter settings of examples

4.2 电池仓库的能量管理策略分析

电池仓库的竞价策略和各时段的充放电功率如图6所示。其报价曲线走势与消纳风电后的基本负荷曲线基本一致。在负荷低谷时，常规机组的报价较低，电池仓库可以通过较低的报价获得充电功率，此时出清电价较小，充电成本也较低。在负荷高峰时，机组的报价也较高，此时出清电价较高，电池放电可以获得较大的收益。

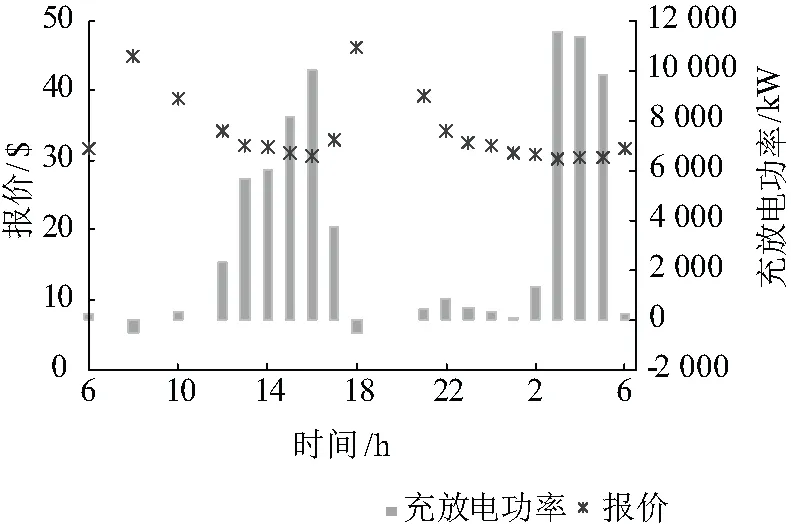
图6 电池仓库报价和能量管理策略Fig.6 Quotation and energy management strategies of battery warehouse

而电池仓库仅在两个电价峰值处出现放电现象，其原因有二:一是由于电池放电导致的损耗成本达到0.01 $/kWh，电池基于出清电价的波动通过高发低储获得的收益大部分时候仍低于损耗成本，电池成本较高、放电损耗较大是制约电动汽车电池参与放电调度的一大重要因素;二是共享电动汽车使用较为频繁，对电池的可调度时段约束较多。由图3可知，从8点～20点，每个时段的换电需求都在200次以上，上午更换下来的电池可能到黄昏就需达到出库的电量标准并配送到相应的服务网点。在白天基本负荷较大时，电池仓库为保证用户需求，其充电功率也较高。

凌晨电价较低，仓库内电池基本都充满电后，可满足上午的大部分换电需求，故而在上午的负荷高峰，充电负荷较小，甚至有余力可参与放电调度。在22点之后，换电需求较小，大部分电池要到次日才需出库配送，故集中在电价最低的后半夜进行充电，少量电池由于需要在夜间出库配送才提前充电。

4.3 不同能量管理模式成本比较

文章对三种不同的能量管理模式进行比较。模式一为前文所述的基于市场出清电价对电池充放电功率进行优化。模式二为仅充电状态下通过参与市场竞价获得的能量管理策略。图7为模式二所得的共享汽车电池仓库的报价和充电策略，其变化趋势与模式一相近。

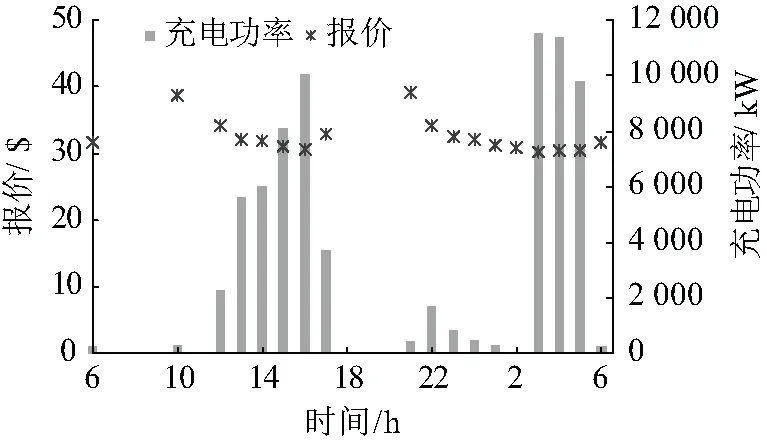
图7 模式二中电池仓库报价和充电策略Fig.7 Quotation and energy management strategies of battery warehouse under mode two

模式三为无序充电状态，即电池返回电池仓库后立即以额定功率开始充电，达到电量上限后断开连接，同样参与市场出清基于出清电价计算成本。三种模式均基于出清电价进行充电费用结算，由于电池仓库的规模较小，其能量管理模式的变动很难对出清电价造成影响，而由KKT条件的式(16)可知，该出清模型中电池仓库的报价与出清电价相等，因此三种模式下同一时段的报价是相同的。模式三中共享汽车电池仓库的成本为2 382.63美元，模式二的成本为2 258.01美元，模式一的成本为2231.08美元，相比于无序充电模式，文中所提的能量管理优化方法可以使成本下降6.4%，有助于共享电动汽车运营商降低运营成本，提高利润空间，可以为共享电动汽车未来的发展模式提供参考。

4.4 电池损耗成本的影响分析

图8为单位电池损耗成本下降50%后电池仓库的报价和充放电策略，其变化趋势与图6相近。在电价相对较高时，图6中由于损耗成本偏高，充放电功率为0的时段，在图8中均参与了放电调度，放电功率相比图6有了很大的提升，可见电池损耗成本极大地影响了参与放电的积极性。近年来，动力电池的技术经济性能提升很快，随着未来电池成本的进一步下降，参与放电带来的收益将会大幅提高，成为共享电动汽车运营的一个新的效益来源。

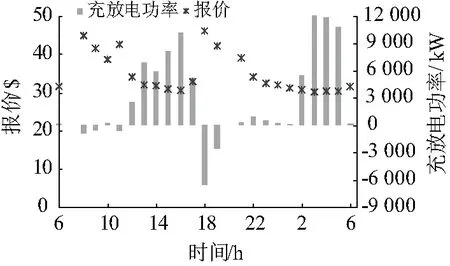
图8 单位电池损耗成本下降50%后电池仓库报价和充放电策略Fig.8 Quotation and energy management strategies of battery warehouse after battery loss cost drops by 50%

5 结束语

基于换电模式的共享电动汽车是未来发展的重要方向，文章对换电所需的电池仓库开展研究，提出了电池仓库能量优化管理的双层规划模型。上层以电池仓库成本最小化为目标对电池充放电功率进行优化，下层实现了电池仓库参与电力市场的出清过程。基于KKT条件和强对偶理论将模型转换成混合整数线性规划问题，调用CPLEX进行优化求解。最后，通过算例仿真分析了电池仓库的竞价和充放电策略，验证了文中所提的能量管理策略可以在满足共享用户电池需求的同时，降低共享汽车电池仓库的运营成本。随着未来电池技术的发展，电池成本的进一步下降，共享电动汽车运营商通过电池仓库参与电网充放电调度的积极性显著提高，可以为运营商缩减成本，为共享电动汽车换电模式的发展提供参考。此外，未来共享电动汽车规模的扩大，换电模式的大规模应用后，可以通过广义纳什均衡模型实现电池仓库集群与发电商的博弈，进而影响出清电价，将在后续展开深入研究。