局部阴影下光伏电池最大功率点跟踪方法

李刚，李超臣，王雅文，何一卓

(吉林大学 仪器科学与电气工程学院， 长春 130021)

0 引 言

随着社会的发展，人类的生活与科技越来越依赖于能源的使用，但由于化石能源的存贮量愈发减少以及对煤炭类的一次能源的重度挖掘利用，能源危机已然化作为世界所需面对的严峻问题。太阳能作为一种绿色能源，以其永不枯竭、环境友好等优点得到广泛重视。光伏发电是太阳能利用最常见的形式之一，最大功率点跟踪(MPPT)作为光伏电池发电的一个重要优化领域备受关注。由于受房屋、植物等的投影覆盖，局部乌云、表层尘土等的干扰，光伏阵列中经常会出现局部阴影。在这种情况下，光伏系统具有多个局部最大功率点，即它的功率-电压(P-V)曲线呈现出多峰的特性[1-2]。此时，简单的传统MPPT算法难以快速准确地寻找到并工作在最大输出功率点，从而极大地影响了系统的效率和可靠性。据统计，在目前市场流通的光伏电池中，由非均匀光照导致的功率损失占总功率损失70%左右[3]。在光伏电池悠久的发展历程中，效率一度成为衡量电池可用性的标准之一，其重要性不言而喻。本课题的研究目的就在于通过搭建仿真模型研究局部阴影对光伏电池工作特性的影响，分析光伏阵列最大功率点的特征，并结合电力电子变换器[4]，设计优化在局部阴影条件下的最大功率点跟踪算法，从而提升效率，降低成本。

传统最大功率点跟踪方法有恒定电压法、扰动观察法和电导增量法[5-6]。恒压法是早期研究出并广泛应用的方法，其主要依据是均匀光照下最大功率点处电压一般在开路电压的4/5左右，据此设计控制电路，使得系统的输出电压稳定保持在0.8Voc附近，但在一些开路电压变化较大的情况下控制精度差，所以现在工程上很少使用。扰动观察法基本工作原理是在每个控制间隔内先增大或者减小光伏电池的电压或电流，之后依据功率变化的方向决定下一步的电压或电流变化的方向。扰动观测法易于实现，但由于“扰动”的存在，会造成电路最终的状态是波动的，无法完全稳定，导致损失功率、降低效率。电导增量法的依据是光伏系统的功率-电压曲线在最大功率点处斜率等于零，此方法精确度高，但控制电路较为繁复，且对硬件要求较高。

上述的传统MPPT算法均有效利用了光伏系统的各种特点，有不同的巧妙之处，但也均各自存在着缺陷，且仅适合于光照均匀输出曲线单峰的情况，但另一方面，一些复杂光照条件适用的跟踪算法常常与这些传统算法的思路有着密不可分的联系。

国内外对局部阴影下最大功率点跟踪的解决方法主要分为三类[7-10]。第一类：通过给阵列附加硬件补偿电路来改变局部P-V曲线多峰的性质，之后再利用传统的跟踪算法[7]。文献[8]中给出各组件并联补偿电路，当光伏阵列被遮挡一部分时，补偿电路工作，受到阴影组件的端电压就得以保持。通过此方法光伏电池的P-V曲线就被矫正为单峰，避免了多峰的出现，从而使用传统方法能让光伏系统工作在最大的功率点附近。但采用此方法时，由于并联了大量的补偿电路，整个光伏发电系统变得复杂，从而导致造价过高；第二类：对阵列结构的优化组合法。文献[9]采用重新构建系统组件的方法削弱非均匀光照对系统输出带来的变化，但该方法的灵活性和应对环境突变能力通常较弱；第三类：采用可以在多峰情况下搜索全局的MPPT算法。其中文献[10]介绍了基于粒子群的跟踪算法，在局部发生阴影的情况下比传统的跟踪算法更加高效、准确。

文中分析了光伏电池基本单元的等效模型，光伏阵列的输出特性，研究了基于改进粒子群算法的局部阴影下光伏电池最大功率跟踪算法，建立仿真模型，进行算法仿真验证。

1 光伏电池模型

单二极管光伏电池数学模型的等效电路模型如图1所示。图1中Iph为光生电流源、Rsh为硅晶缺陷产生漏电流的电阻，Rs为等效的串联电阻。

图1 单二极管等效电路Fig.1 Single diode equivalent circuit

根据 KCL 定律可得光伏电池输出电流为:

I=Iph-Id-Ir

(1)

式中，

(2)

(3)

Id=I0(eq(U+IRs)/akT-1)

(4)

(5)

上式为单二极管模型的数学关系式[11-12]。其中，Isc为短路电流；I0为反向饱和电流；S为光照强度；T为所处环境温度；α为二极管品质因数；q为电子电量；K为玻尔兹曼常数(1.38 ×10-23J/K)。

上述的单二极管模型精度较高，但若应用于实际工程则显得较为复杂。由于Rsh阻值极大且对输出特性影响较小，为了简化，在工程应用中可忽略漏电流。而Rs的改变会给P-V 特性曲线带来很大变化，因此等效串联电阻必须保留。综上，简化后得工程数学模型关系式为：

I=Iph-I0(eq(U+IRs)/akT-1)

(6)

制造商通常在包装上只提供用户获取光伏组件在标准条件下测试出的最大功率Pm、最大功率点电流Im、最大功率点电压Um、开路电压Uoc、短路电流Isc的值[11]。由此，常令I0=C1Isc，akT/q=C2Uoc，则式(6)可表示为：

(7)

其中，

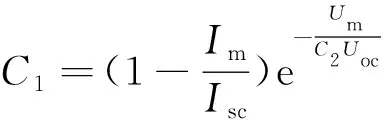
(8)

(9)

dv=-βdt-Rsdi

(10)

(11)

dt=Tc-Tref

(12)

式中α表示电流变化温度系数(A/℃)，β表示电压变化温度系数(V/℃)；S代表当前的太阳照度;Tc表示此时的环境温度(℃);Sref、Tref分别为系统光照度和温度的参考值，标准情况取值为1 000 W/m2和25 ℃。

2 光伏阵列局部阴影下输出特性

首先分析相互串联和并联的两个光伏组件发生局部阴影的情况。

图2(a)是存在局部阴影的由两个组件并联组成的光伏阵列。其中，PV2受到遮挡，因此PV1的开路电压、短路电流就会大于PV2的开路电压和短路电流[17]，即Voc1>Voc2，Isc1>Isc2。VDs1和VDs2是针对热斑效应设置保护的阻塞二极管。

图2 两光伏组件串并联阴影影响分析Fig.2 Analysis of shadow influence of two photovoltaic modules in series and parallel

图3绘制出了两个光伏组件PV1(光照强度1 000 W/m2)和PV2(光照强度500 W/m2)单独运行及并联运行时的电流-电压、功率-电压输出特性曲线。当系统的总输出电压低于遮阴组件的开路电压Voc2时，两个光伏组件就都处于输出的工作状态，此时的电池总输出电流为并联组件PV1和PV2电流之和；而当系统的总输出电压大于遮阴组件的开路电压时，PV2将无法继续工作，此时只有PV1处于输出的工作状态，电池总输出特性就和PV1单独工作时的输出特性一致。因此，对于光伏阵列来说，并联的光伏电池串可以相对独立的工作，当仅仅是某条或某几条并联支路整体处于阴影情况时，整个电池的输出P-V曲线仍呈现单峰值的特性。

图3 局部阴影下两并联组件输出特性Fig.3 Output characteristics of two parallel modules under partial shadow conditions

图2(b)是存在局部阴影的由两个组件并联组成的光伏阵列。其中，PV2受到遮挡，因此同样的，Voc1>Voc2，Isc1>Isc2。VDp1和VDp2是针对热斑效应设置保护的旁路二极管。图4绘制出了两个光伏组件PV1(照度1 000 W/m2)和PV2(照度500 W/m2)单独运行及串联运行时的I-V、P-V输出特性曲线。当系统的总电流小于短路电流Isc2时，则旁路二极管均不工作，两组件上流经的电流大小相同，它们一起处于输出状态，整个电池的输出电压为组件PV1与PV2的电压之和；当ipv>Isc2时，为防止PV2成为负载消耗功率，二极管VDp2开启并将受遮挡组件旁路，此时只有未受遮挡组件PV1处于输出状态，整个电池的输出特性和PV1输出特性一致。

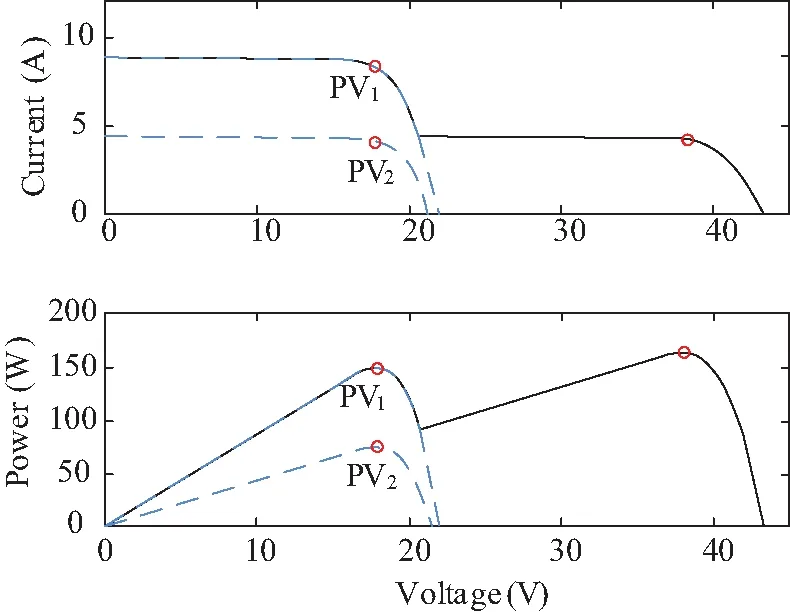
图4 局部阴影下两串联组件输出特性Fig.4 Output characteristics of two series modules under partial shadow conditions

由以上分析可知，当串联的光伏组件发生局部阴影时，若光伏系统的工作电流大于被遮挡组件的电流时，遮阴的组件将不再工作。这就导致了光伏电池的I-V曲线呈阶梯状，P-V曲线出现多个局部极值并会产生奇点。且结合式(7)，对于各光伏组件之间是串联关系的阵列，局部遮阴情况下的表达式可体现为有关电流的分段函数：

(13)

式中N2为旁路二极管导通前参与发电的串联组件数；N1为旁路二极管导通以后参与发电的串联组件数。在图2(b)所示情况中，N2=2，N1=1。

可由此推知由m个光伏组件串联的光伏电池在局部阴影情况下P-V曲线的特性。假如这m个光伏组件受最多种(m种)不同光照强度的影响，随着输出电流的增大，阵列中工作的光伏组件将越来越少，导通的旁路二极管越来越多，最后直至受到阴影的m-1个组件全部被旁路。此时，整个光伏电池的输出P-V特性曲线将呈现m个峰值，即由m个光伏组件串联的光伏电池的输出功率曲线至多存在m个峰值。

4串2并光伏阵列如图5所示，对8个光伏单元设置了6种不同的阴影情况，如表1所示。不同阴影下4串2并光伏系统输出特性如图6所示。通过以上分析，4×2的光伏阵列最多有4个峰值。

表1 各光伏组件光照强度情况Tab.1 Light intensity of each photovoltaic module

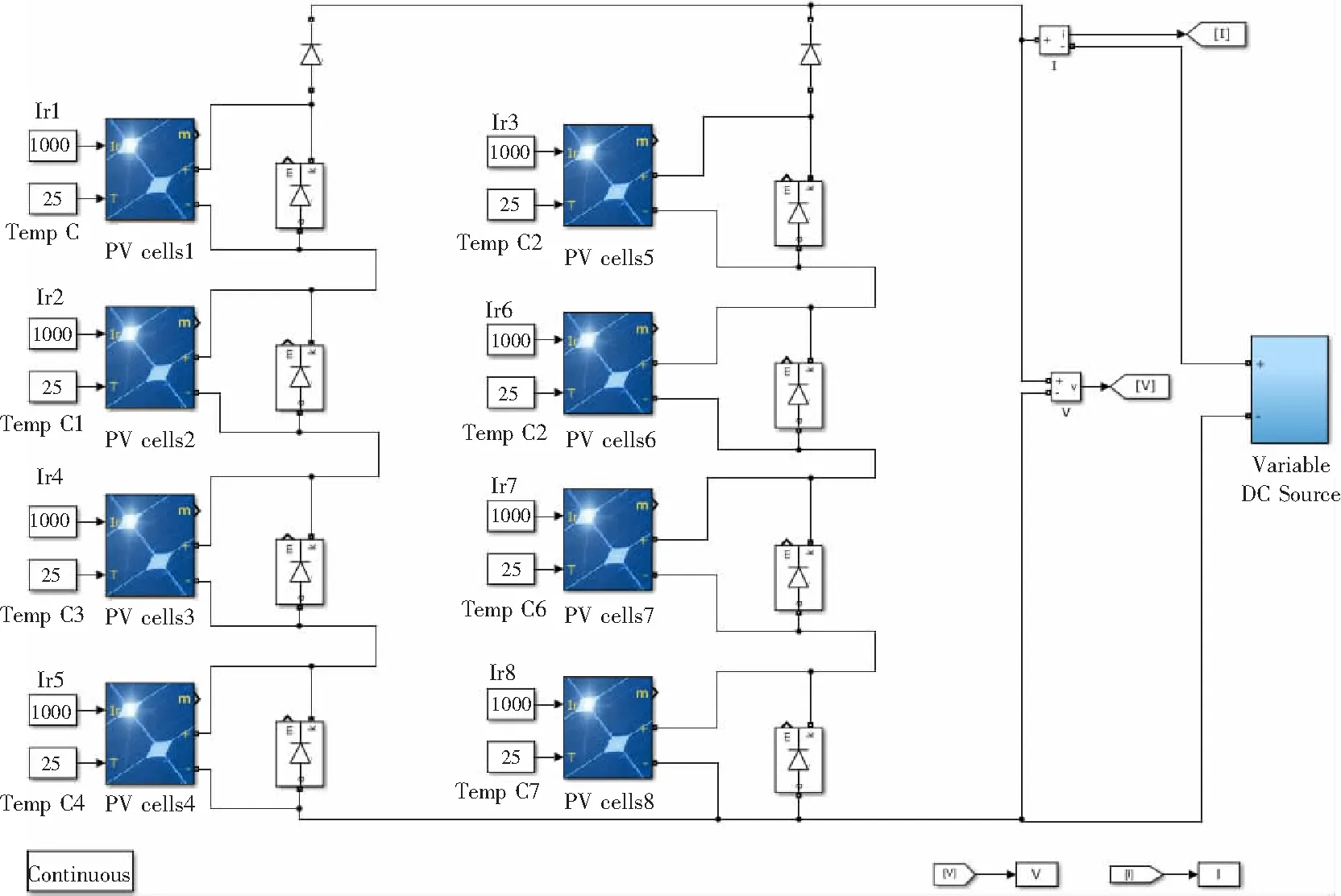
图5 局部阴影下4×2光伏系统Fig.5 4-series 2-parallel photovoltaic system under partial shadow conditions

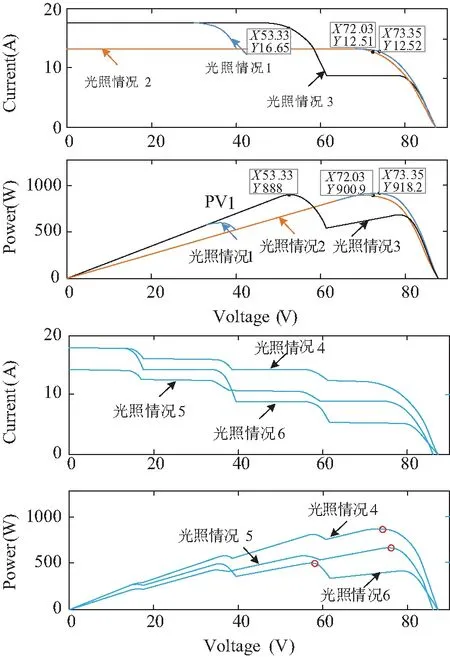
图6 不同阴影下4串2并光伏系统输出特性Fig.6 Output characteristics of 4-series 2-parallel photovoltaic system under different shadows

3 局部阴影下光伏电池最大功率跟踪算法

粒子群优化算法(Particle Swarm Optimization，PSO)最初的目的是模拟社会行为，它也是基于迭代法，通过不断尝试来逐步优化可能解，向更优的位置逼近，从而最终确定最优解。

从原理上来说，粒子群算法[7]类似于模拟鸟群寻找食物。每个粒子的属性包括其自身的位置、速度和适应度函数。适应度函数根据具体目标要求设定；粒子的速度决定其运动距离和方向[13]。每个粒子的运动受其自身历史最优位置(Pbest)的影响，同时也被引导到整个搜索空间中全局最优的位置(Gbest)，这些最优位置都会随着迭代而更新[14]。

其中，粒子的速度和位置更新公式如下：

(14)

(15)

式中w表示惯性权重；d表示空间维数；i为粒子标识；r为随机数(在0～1之间取值)；k表示迭代次数。式中Pi和Pg有如下定义：

(16)

Pg∈{P1,P2,...,Pn}，f(Pg)=max[f(Pi)](1≤i≤n)

(17)

将粒子群算法应用于最大功率点跟踪算法[15]，维数d在文中是一维，式中当前位置Xik就代表粒子i当前的电压Ui；速度vi是i粒子的电压增量ΔUi；Pi是每个粒子自身搜寻到历史最大功率对应的电压；Pg是所有粒子搜寻到的最大功率对应的电压。

将粒子群算法应用于MPPT中的具体流程如图7所示。局部阴影下粒子群算法的MPPT跟踪结果如表2所示。

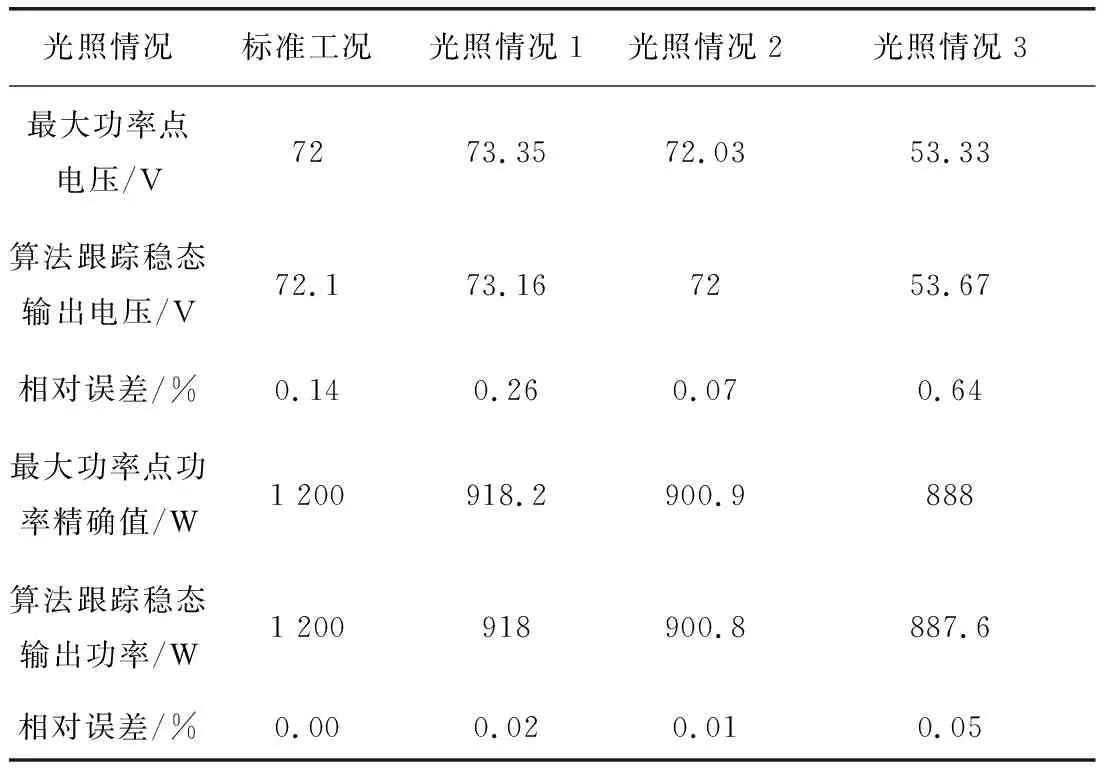
表2 局部阴影下粒子群算法的MPPT跟踪结果Tab.2 MPPT tracking results of particle swarm algorithm under partial shadow conditions

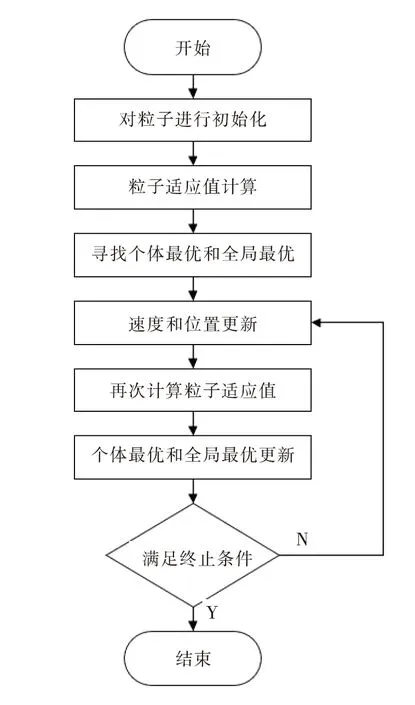
图7 粒子群算法流程图Fig.7 Particle swarm algorithm flow chart

(1)初始化。参考相关文献中的经验和不断调试为粒子群算法中各个参数赋值，并设置初始速度及初始位置等[11]；

(2)评价粒子。通过公式计算出不同位置(电压)粒子的适应度(功率)，由式(16)和式(17)比较出每个粒子自身搜寻到最大功率对应的电压pbest和所有粒子搜寻到的最大功率对应的电压gbest，并把这些电压及对应的功率存储下来；

(3)更新粒子。根据式(14)和式(15)更新粒子电压Ui的和电压增量ΔUi，如果粒子的电压超过设定的上下限，则在下一时刻仍令其维持在此刻的位置；

(4)重新计算适应度。重新计算处于新电压的粒子的功率，并和历史自身最大功率、全局最大功率比较，更新pbest和gbest；

(5)检验是否终止。若算法达到了程序中设置的收敛精度或最大次数，那么迭代终止并使电路工作在最大功率点对应的电压。如若未达到，即跳转回步骤(3)继续迭代计算。

4 仿真结果

算法采用3个粒子，初始化时将3个粒子均匀分布在最大功率点可能出现区间。在粒子群算法中惯性权重w表示的是下一刻粒子对本时刻自身的继承度，是PSO算法较为重要的参数之一，w若设置过小，初期收敛速度慢且较易引导到局部功率峰值点，w若设置过大，后期收敛会变得更加波动，难以得到精确解[16-17]。w一般在[0.4,1.2]之间取值[18]，在本算法中，经过调试，取惯性权重w=0.5。c1设置的是每个粒子向自身最优逼近的重要程度，c2设置的是每个粒子向全局最优逼近的重要程度，它们分别代表着粒子的自我认知以及社会认知对下一时刻去向的影响，这两个学习因子一般在[0,4]之间取值[16]，在本算法中，经过调试，取值为c1=0.15，c2=0.35时不易陷入局部极值点，且后期波动较小。为了防止算法过分偏离正轨，还需要设置上下限，上限为90 V，下限为30 V，若超过范围，则维持当前电压。根据仿真结果，给PWM模块输入不同的电压，电路均能在0.08 s前达到稳定，因此在输入当前粒子的电压后的0.08 s采样功率P作为适应度函数。

如图8(a)所示，在其中1串光伏阵列的阴影度为50%时，在2 s左右，电路基本达到稳定运行状态，最终跟踪到的最大功率为918 W，工作电压73.16 V，与图8(b)中的精确值(最大功率为918.2 W，工作电压73.35 V)比较，误差小于1% ,证明了粒子群算法跟踪的可靠性。

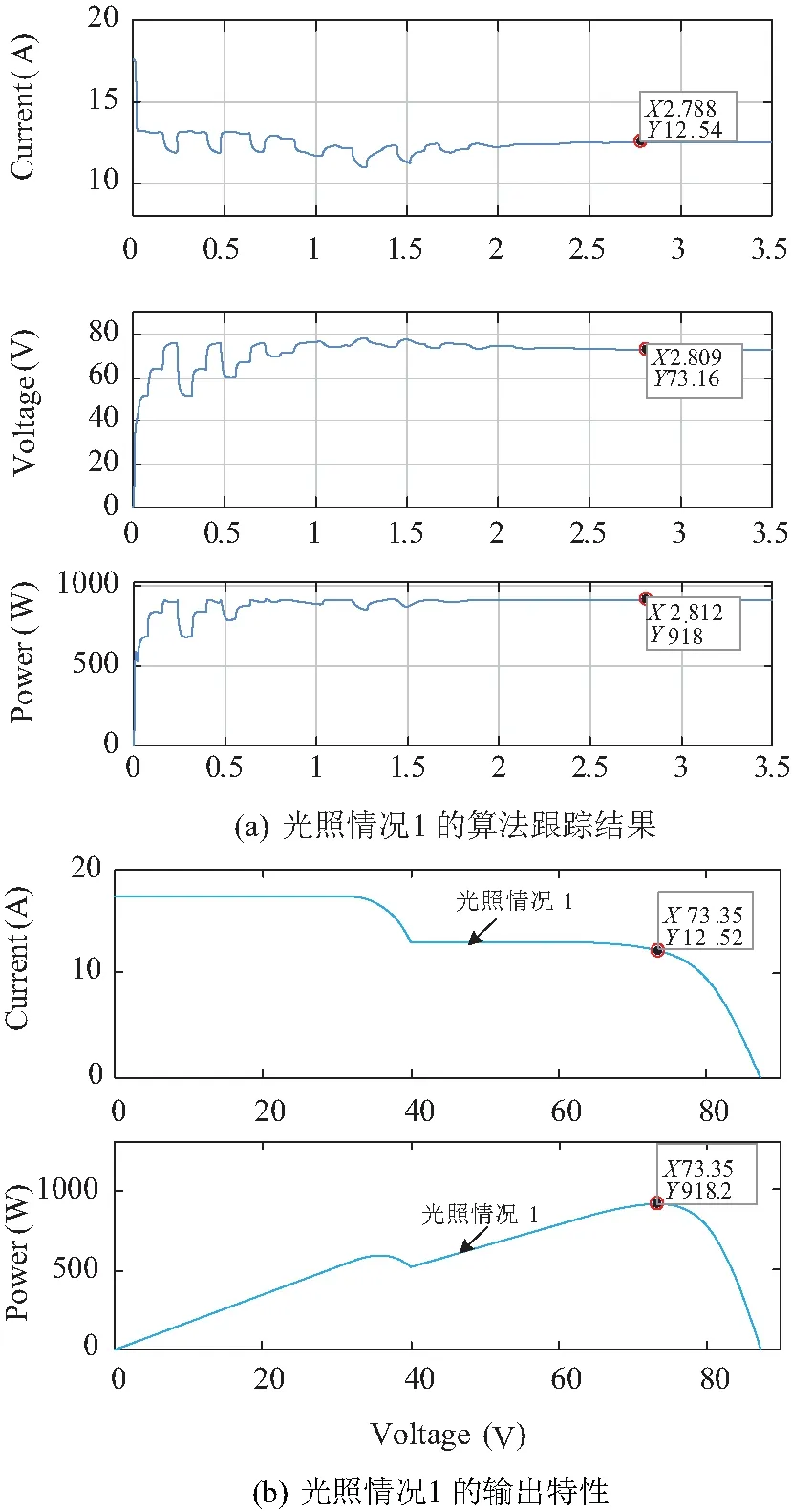
图8 光照情况1时跟踪结果与精确结果对比Fig.8 Comparison of tracking results and accurate results in light condition 1

如图9(a)所示，在并联支路两相邻光伏模块局部阴影时，在2 s左右，电路基本达到稳定运行状态，最终跟踪到的最大功率为887.6 W，工作电压为53.67 V，与图9(b)中的精确值(最大功率为888 W，工作电压53.33 V)比较，误差小于1%，证明了粒子群算法跟踪的可靠性。

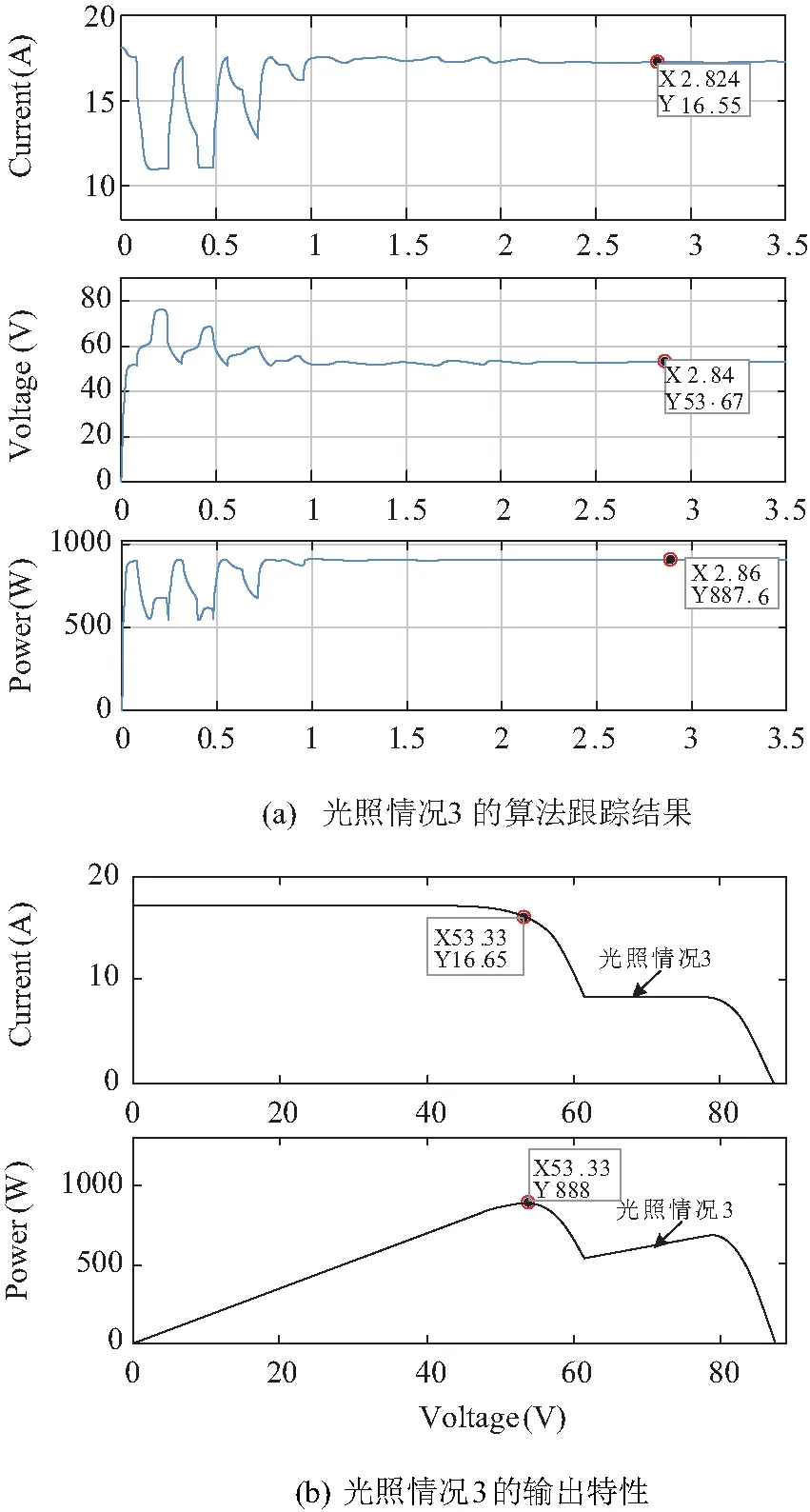
图9 光照情况3时跟踪结果与精确结果对比Fig.9 Comparison of tracking results and accurate results in light condition 3

由仿真结果，不同阴影情况下电压和功率的相对误差均小于1%，因此，在局部阴影情况下文中提出的算法能够相对准确地跟踪到系统的最大功率点。

粒子群算法由于各粒子搜寻到的自身历史最大功率和种群历史最大功率是不断更新并保留下的，因此，若阴影情况发生突变，各粒子却仍会将当前功率与历史最大功率对比，从而会导致算法失灵。基于以上问题，进行了进一步拓展研究，使算法能根据阴影的变化重新初始化，最终改变工作点。由于以上设计的算法基本可在2.8 s内到达相对误差1%以内的稳定状态，因此设置在2.8 s后可以开始检测当前光照情况是否发生变化，如有变化则再次初始化重新追踪，如无变化则保持当前状态直至光照情况发生变化。图10是光伏组件4和组件8的光强初始为1 000 W/m2(表2中的标准工况)，在3.5 s时突变为500 W/m2(表2中的光照情况3)的仿真结果，跟踪误差小于1%。

图10 动态阴影变化下的MPPT仿真结果Fig.10 MPPT simulation results under dynamic shadow changes

5 结束语

文中通过建立光伏电池模型，分析相互串联和并联的两个光伏组件发生局部阴影情况，搭建了一个4串2并结构的光伏系统，探究其在局部阴影下的输出特性并将粒子群算法应用于最大功率点跟踪，最终通过仿真证明在局部阴影情况下，文中提出的算法能够相对准确地跟踪到系统的最大功率点。