基于多周期性MILP模型的新型配电系统拓扑辨识方法

萧展辉，邹文景，唐良运

(南方电网数字电网研究院有限公司，广州 510000)

0 引 言

新型配电系统是深度融合了分布式能源、柔性负荷、新型储能、柔性多状态开关等设备的复杂系统[1-2]，其结构更趋复杂、潮流分布极不确定、调控节点更加细密。配电系统的状态估计、故障定位、电压/无功控制等功能的实现都严重依赖于准确的拓扑结构，因此，拓扑辨识(Topology Identification, TI)[3]对于新型配电系统的运行控制至关重要。然而，在实际工程中，由于配电系统的测量数据有限、配电馈线上开关和断路器的状态信息不可用、不可靠，使得准确辨识配电系统的拓扑结构十分困难。

在实际工程中最常用的拓扑辨识方法是配电网运维人员现场查看馈线上开关和断路器的开断状态，这种做法虽然简单可靠，但不能持续地跟踪配电系统拓扑结构的变化。因此，基于量测的拓扑辨识方法根据传感器的测量数据来估计馈线上开关和断路器的状态[4-5]。文献[6]基于匹配环路功率确定可能的拓扑结构,并根据公共量测值对可能的拓扑结构进行状态估计。文献[7]基于支路有功功率残值的大小选择可能断开的支路，得到若干种可能拓扑结构,在每个可能拓扑结构下分别进行状态估计。文献[6-7]中的拓扑辨识方法主要是根据传感器量测数据对可能的拓扑结构进行状态估计，在状态估计中根据最小残差来选择拓扑结构。然而，这类基于状态估计的拓扑辨识方法需要足够的量测数据来提高状态估计的准确性，这对于分支众多的配电系统来说，安装足够多的传感器去获取量测数据显然不可取。为此，也有文献采用有限的量测数据来实现拓扑辨识。文献[8]通过对电压序列的动态时间弯曲距离进行聚类分析，自动识别低压用户所属台区，得到正确的低压配电台区网络拓扑结构。文献[9]通过在每类台区内采用Tanimoto相似度系数计算各台区内设备的相似性及隶属关系，从而实现相关台区的拓扑辨识。文献[10]用皮尔逊相关系数判断用户电压序列曲线的相似性，通过相关系数算法来辨识台区户变关系。但这类拓扑辨识方法也需要积累一定数量的电压样本，存在辨识分辨率不高、计算量大等问题。

随着大数据以及配电系统高级量测体系技术的发展，已有文献从各台区的电压、电流的时空特性数据挖掘出隶属关系，实现拓扑辨识。文献[11]通过建立基于KCL的优化模型，并将其转化为二次规划问题求解，实现低压配电网线户关系识别。为了克服数据缺失问题，文献[12]利用知识图谱技术对多个低压配电网信息系统中的数据进行整合，推理出缺失数据，挖掘出各数据之间的关联建立拓扑结构。文献[13]建立了基于节点多时段有功、无功负荷和电压幅值量测的非线性参数估计模型，提出了配电网拓扑重建算法。文献[14]提出了一种配变互联关系辨识的集成深度神经网络模型，提高了灵活网络的拓扑辨识精确度。文献[15]利用支持向量机多分类模型来辨识量测数据所对应的拓扑。可见这些拓扑辨识方法均是通过数据重构拓扑，缺乏内在的机理解释，对数据的纠错能力有限[16-17]。

从上述文献也可以看出，考虑测量电流的拓扑辨识方法的数据容错能力有待提升。随着新型配电系统馈线终端FTU上升级改造之后配置宽带电压传感器、宽带电流传感器。与测量电压和功率的传感器相比，宽带电流传感器的成本更低且更易于安装，非接触式电流传感器还可以测量电场，可用于估计当前测量的相对相位角。换句话说，这些电流传感器可以估计相量，就像u-PMU[18]。为此，文中提出一种基于支路电流的配电网拓扑辨识方法。在构建基于支路电流测量的背景下，建立了拓扑辨识的多周期性混合整数线性优化模型，提高了拓扑辨识的精度和鲁棒性，IEEE-33节点系统的仿真测试验证了文章方法的优势。

1 基于支路电流的新型配电系统拓扑辨识

1.1 拓扑辨识的MINLP模型

假设配电系统中所有线路的开关处于闭合状态。根据基尔霍夫电流定律(KCL)，注入每个节点的电流等于与该节点相连接的线路的支路电流总和：

(1)

式中Ii为节点i的注入电流；Iij为线路(i,j)的支路电流；Ni为与节点i相连接的节点集合；N为配电系统所有节点。

线路(i,j)流过的支路电流Iij取决于线路的开关状态、两个节点的电压以及线路的导纳。根据基尔霍夫电压定律(KVL)，可得：

Iij=sij(Vi-Vj)yij

(2)

式中sij表示线路(i,j)的运行状态，sij为1表示在运行；否则为0，保证Iij为0；Vi、Vj分别表示节点i、j的节点电压；yij为线路(i,j)的导纳。

根据节点电压Vi和节点注入电流Ii，可以得到节点注入功率：

(3)

式中Si表示节点i的负荷注入功率；bi表示节点i与系统的连接状态，如果节点i连接到网格，则bi为1；否则为零，表示存在孤岛节点。在这种情况下，拓扑辨识方法可以确定停电区域；从而将其扩展到基本拓扑辨识，形成拓扑辨识问题的优化模型：

(4)

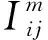
1.2 拓扑辨识的MILP模型

拓扑辨识的MINLP模型式(4)是一个典型的混合整数非线性优化问题，本节将此模型转换为更易于求解的MILP模型。

式(2)中的非线性是由于0-1变量sij与连续相量变量Vi和Vj的乘积。为了消去这种非线性，将式(2)代入以下线性方程：

Iij=yijUij

(5)

式中Uij为一个辅助变量，相当于sij和Vi-Vj的乘积。如果sij=1，即如果线路(i,j)处于闭合状态，则Uij=Vi-Vj，否则Uij=0。Uij、sij和Vi-Vj之间的上述关系可以通过添加以下线性约束来消去非线性项[19]：

-M(1-sij)≤Re{Uij}-Re{Vi-Vj}≤M(1-sij)

(6)

-Msij≤Re{Uij}≤Msij

(7)

-M(1-sij)≤Im{Uij}-Im{Vi-Vj}≤M(1-sij)

(8)

-Msij≤Im{Uij}≤Msij

(9)

因为Uij和Vi-Vj是复数变量，所以式(6)～式(9)中的方程分别采用Re和Im取实部和虚部。如果sij=0，则约束条件式(6)和式(8)不起作用；从约束条件式(7)和式(9)中可得到Uij=0，同时Iij=0。因此，当sij=0时，强制执行式(2)中的非线性等式约束。如果sij=1，则约束条件式(7)和式(9)不起作用；从约束条件式(6)和式(8)中可以得到Uij=Vi-Vj，因此有Iij=(Vi-Vj)yij。因此式(2)中的非线性等式约束也在sij=1时强制约束，式(5)～式(9)中的线性约束等价于式(2)中的非线性约束。

拓扑辨识的MINLP模型式(4)的另一个非线性项是约束条件式(3)中相量Vi和Ii的乘积，即非线性潮流约束。非线性潮流约束的线性化方法很多，但需要适应不同的拓扑结构，而且分支电流必须保留。为此，采用文献[20]中的线性化方法，该方法基于复数域的泰勒展开，而不是在实数域的潮流方程进行泰勒展开。假设节点i的电压在额定电压1 pu附近，可以表示为：

Vi=1-ΔVi

(10)

通过应用泰勒级数并忽略高阶项，可得到：

(11)

这种复数域的泰勒展开近似的精度可以通过潮流解来进行验证，其近似误差为：

(12)

在文献[20]中绘制出了误差指标如图1所示。

图1 验证式(11)中线性化的准确性：Fig.1 Validating the accuracy of the linearization in formula(11)

图1(a)为以1.0为圆心，在ΔVi为半径的圆盘内的每个点进行评估，得到图1(b)中的误差区域。例如，在ΔV=0.1 p.u.时，近似误差仅为1%左右。实际中ΔV通常小于0.05 p.u.，因此，逼近误差小于0.3%，这是满足工程潮流计算的精度要求。

将式(11)代入式(3)可得：

(13)

然而，由于0-1变量bi和相量变量Vi相乘，上述方程仍然是非线性的。因此，引入一个新的辅助变量Wi， 将式(13)替换为如下线性方程：

(14)

式中Wi等价于bi和Vi的乘积。如果bi为1，即如果节点i连接到系统，则Wi=Vi；否则Wi=0，表示该节点未连接到系统。Wi、bi和Vi之间的上述关系可以通过增加如下线性约束来实现：

-M(1-bi)≤Re{Wi}-Re{Vi}≤M(1-bi)

(15)

-Mbi≤Re{Wi}≤Mbi

(16)

-M(1-bi)≤Im{Wi}-Im{Vi}≤M(1-bi)

(17)

-Mbi≤Im{Wi}≤Mbi

(18)

上述Big-M的方法与式(6)～式(9)的原理基本一样，这里不在赘述。

需要注意的是，式(14)可以保证断开节点的注入电流为零，但不能保证断开节点的电压也为零，因此，还需要添加一组新约束，以确保断开节点的电压为零，即：

-Mbi≤Re{Vi}≤Mbi

(19)

-Mbi≤Im{Vi}≤Mbi

(20)

(21)

(22)

Eij≥0 andFij≥0

(23)

综上所述，拓扑辨识的MINLP模型转化为如下的MILP模型：

(24)

满足式(1)、式(5)～(9)、式(14)～式(23)。

2 考虑伪测量和周期的拓扑辨识方法

2.1 电流传感器的优化配置

从理论上讲，为了辨识配电系统的拓扑结构，每条支路均配置电流传感器，这会造成巨大的投资成本，为此，电流传感器优化配置是为了解决支路电流的可观测性，以便有足够的支路电流数据支撑拓扑辨识的MILP模型。电流传感器优化配置就是明确支路电流传感器的配置支路和数目，从而实现配电系统支路电流的可观测性，从而准确地辨识拓扑。文章证明了配电系统支路电流可观测性的必要条件是在配电系统的每个独立回路中至少配置一个电流传感器，则配电系统的拓扑是可以准确辨识的。证明过程如下：

证明：一个电路中有N个节点和L条支路，则需要L个独立方程来获取支路电流。从N个节点的注入电流方程中，N-1个方程是独立的[21]。因此，为了获取L个独立的支路电流方程，需要L-(N-1)个额外的独立方程，因此，通过测量L-(N-1)条支路电流来获得独立方程。

回路是从一个节点开始，经过一组节点后，返回到初始起始节点的闭合路径，且一个至多经过一次。如果一个回路本身不包含任何回路，则称该回路是独立的。在电路理论中，独立回路产生独立的KVL方程。因此，只需要电流传感器测量到独立回路中的L-(N-1)条支路电流，就可以推算出所有支路电流。

对如图2所示的一个独立的回路，假设节点注入电流为I1,I2,...,In已知，要得到回路中每条支路的电流，In,1,I1,2,...,In-1,n，根据KCL可得：

图2 n个节点组成的独立回路，电流传感器配置在支路{i-1,i}以测量Fig.2 An independent loop consisting of n nodes, the current sensor is installed at branch {i-1,i}

(25)

(26)

与式(25)不同，式(26)具有唯一解。因此可以得出在独立回路中的任意支路配置一个支路电流传感器，就可以附加一个独立方程到回路的KCL方程中。由于网络中有L-(N-1)个独立回路；在每个独立回路配置L-(N-1)个支路电流传感器，为可以推算出所有支路电流。

接下来用简单的电路例子来说明配电系统支路电流可观测性的必要条件。如图3所示。

图3 由4个节点和2个回路组成的电路Fig.3 A circuit with 4 nodes and 2 loops

在节点数N=4、支路L=5的电路中，用l1表示的回路1231和用l2表示的回路1341是两个独立回路。需要注意的是回路12341不是一个独立回路，因为它在其内部包含其他回路l1或l2。则该网络的KCL方程组如下：

(27)

表1 图3中网络的电流传感器配置方案Tab.1 Current sensor configuration scheme of the network in Fig.3

2.2 考虑伪测量误差的拓扑辨识方法

为了解决测量和伪测量中误差的影响，将式(1)中的注入电流约束以惩罚项的形式添加到目标函数中，有：

(28)

通过采用与第1.2节中类似的方法将式(28)的绝对值线性化处理，定义辅助变量Gi和Hi， 并增加以下线性约束条件：

(29)

(30)

Gi≥0，Hi≥0

(31)

考虑测量和伪测量中误差的拓扑辨识的MILP模型进一步改写为：

(32)

2.3 考虑测量周期性的拓扑辨识多周期优化方法

式(32)中拓扑辨识的MILP模型是针对单个时间周期的，在实际中，支路电流测量值可能在配电系统拓扑变化后的初始时刻继续采用。拓扑辨识需要考虑测量的多周期性问题，以更好地减轻测量误差和伪测量的影响。T表示测量和伪测量的周期数，[t]表示每个时刻t对应的数据，t=1…T，让Ψ[t]表示在t时刻式(32)中的目标函数。因此，考虑测量周期性的拓扑辨识MILP模型表示为：

(33)

满足式(5)～式(9)at[t],t=1,…,T,式(14)～式(23)at[t],t=1,…,T,式(29)～式(31)at[t],t=1,…,T。

式(33)可以看成是基于多场景的优化模型，其中γ[t]表示与场景t相关的概率。如果不同场景的随机性服从均匀分布，则可以选择γ[t]=1/T,∀t=1,...,T；否则，可以使用已知的非均匀概率分布。这是由于每个节点负荷存在随机性，测量值和伪测量值会随机变化，每个场景都会为这些随机负荷变量生成一个新的随机场景，在估计开关状态时提供冗余。

3 仿真分析

采用IEEE-33节点标准算例来验证所提出的拓扑辨识方法，接线示意图如图4所示，所有支路开关的状态采用实线和虚线表示，常闭合开关用实线表示，常开开关用虚线表示。图4中由标记为l1～l5的五个回路组成，支路电流传感器配置在支路在<8>、<13>、<20>、<24>和<29>上。由于该配电系统中有21个开关，因此可以创建221种不同的拓扑，其中选择了65种拓扑配置，包括50个辐射状、10个回路和5个孤岛。除了电流测量之外，假设所有负荷注入都可以通过伪测量获得。

图4 IEEE-33节点测试系统Fig.4 IEEE-33 node test system

本节的拓扑辨识算法在Matlab软件中实现，并调用intlinprog函数求解式(24)、式(32)和式(33)中的MILP模型。在仿真中：

(34)

(35)

这保证了99.7%的ei值落在真实值的±ηi百分比范围内。此外，拓扑辨识方法的精度定义如下：

(36)

在实际中，伪测量通常是基于智能电表数据或历史数据的短期负荷预测获得的，采用蒙特卡罗方法生成不同的场景，针对任何给定的测量不准确度验证文所提出的拓扑辨识算法的鲁棒性。

在仿真测试中假设伪测量误差在10%～50%的范围内，评估所提出的拓扑辨识算法在不同伪测量误差下的精度。表2给出了在不同伪测量误差下的拓扑辨识精度。不难看出：如果伪测量误差低于30%，拓扑辨识精度高达98%左右，随着伪测量误差增加到50%，那么拓扑辨识精度会显著下降；使得拓扑辨识结果不可靠。当然，在如此高的伪测量误差下，失去拓扑辨识精度也是不可避免的。

表2 在不同伪测量误差下的拓扑辨识精度Tab.2 Topology identification accuracy under different pseudo measurement errors

伪测量中误差的影响可以通过2.3节所提出的拓扑辨识多周期优化方法补偿。为了测试拓扑辨识多周期优化方法的性能，采用正态概率分布生成伪测量误差，均值为零，标准偏差为式(35)，求解式(33)中的拓扑辨识的多周期优化模型，每次新的测量场景都可用于更新辨识结果。

图5给出了不同伪测量误差下的拓扑辨识多周期优化方法的精度。随着更多测量场景的增加，拓扑辨识精度逐渐增加。即使伪测量误差达到50%，拓扑辨识单周期优化方法的准确度为77.1%，而多周期优化方法在增加20个测量场景后将准确度提高到了95.0%。当然，求解式(33)中的拓扑辨识的多周期优化模型的计算复杂度随着场景数量的增加逐渐增大，拓扑辨识的多周期优化方法运行10个和20个场景分别需要大约40 s和125 s，这比表2中给出的单周期优化方法运行时间要长得多。

图5 IEEE-33节点测试系统Fig.5 IEEE-33 node test system

进一步，对比了拓扑辨识的多周期优化方法和单周期优化方法，拓扑辨识结果如表3所示，表3中×表示拓扑辨识错误，√表示拓扑辨识正确，在仿真中，IEEE-33节点配电系统拓扑在所有15个场景中保持不变。从表3中看出，拓扑辨识的单周期优化方法仅能辨识出场景6、场景9、场景11和场景13这四个场景的拓扑，其他11个场景的拓扑都辨识错误，这是由于负荷变化和伪测量误差较大而引发的。然而，拓扑辨识的单周期优化方法只要有足够的场景6个就能辨识正确的拓扑。拓扑辨识的多周期优化方法在仅有第一个场景时与拓扑辨识的单周期优化方法相同，在获取第2个场景后，拓扑辨识的多周期优化方法就可以利用第一个和第二个测量场景的组合，依此类推。

表3 拓扑辨识多周期优化方法和单周期优化方法的比较Tab.3 Comparison between multi-period optimization method and single-period optimization method for topology identification

进一步与文献[22]中提出拓扑辨识的MIQP模型进行对比，结果如表4所示，不难发现：文中所提出的拓扑辨识MILP模型比文献[22]中的MIQP模型精度更高，能够削弱伪测量误差造成的拓扑辨识影响。这是因为文献[22]中的MIQP模型中的目标函数的平方和将偏离期望值，而不是像文中最小化绝对误差。此外，MIQP的计算时间比MILP多。从成本效益的角度来看，文献[22]中的MIQP方法需要采用10个支路功率传感器，而文中仅需采用5个支路电流传感器，这也证明了文中方法简单、成本效益高等优势。

表4 文中方法与MIQP模型的比较Tab.4 Comparison between the proposed method and MIQP model

最后，针对支路电流传感器测量误差和伪测量误差共同作用下验证所提出的拓扑辨识方法的性能，这里支路电流测量误差以总矢量误差表示，包括幅度误差和角度误差，拓扑辨识结果如表5所示。从表5可以看出，所提出的拓扑辨识方法受伪测量误差的影响比支路电流测量误差更大。当然，这里认为伪测量的误差要高得多，因为在实际中确实如此。

表5 支路电流传感器测量误差和伪测量误差共同作用下的拓扑辨识精度Tab.5 Topology identification accuracy under the branch current sensor measurement error and pseudo measurement error

4 结束语

在新兴的非接触式、低成本的电流传感器的基础上，提出了配电系统拓扑辨识的多周期性混合整数线性优化模型，IEEE-33节点系统的仿真测试结果表明：

(1)如果伪测量误差低于30%，拓扑辨识精度高达98%左右，随着伪测量误差增加到50%，那么拓扑辨识精度会显著下降,使得拓扑辨识结果不可靠；

(2)随着更多测量场景的增加，拓扑辨识精度逐渐增加。即使伪测量误差达到50%，拓扑辨识单周期优化方法的准确度为77.1%，而多周期性优化方法在增加20个测量场景后将准确度提高到了95.0%;

(3)伪测量误差对所提出的拓扑辨识方法的精度影响较支路电流测量误差更大。