基于多级高阶微分求积法的非线性电磁暂态快速仿真研究

张静，叶婧，殷明，李博文

(1.三峡大学 电气与新能源学院，湖北 宜昌 443002； 2.国网湖北省电力有限公司随州供电公司， 湖北 随州 441300)

0 引 言

随着现代化工业技术的发展，分布式能源的引入，电网结构变得庞大和复杂，而电网不仅可能会受到操作过电压，雷电过电压的冲击，也会面临不同类型的故障带来的影响。为了确保电力系统的可靠运行，为保护整定提供参数，也为了满足电网对实时仿真的要求，对电磁暂态仿真计算速度的研究显得尤为重要。电磁暂态过程一般由一组微分方程表示，极小的仿真步长使得计算效率低下；精度和速度之间的矛盾制约着电磁暂态仿真效率的提高。为了在保证计算精度的同时加快电磁暂态计算速度，研究者在不同方向展开探讨，并取得了可观的结果[1-4]。

并行技术作为一种提高电磁暂态计算速度的有效手段活跃在电磁暂态仿真中。图形处理器(GPU)结合所选算法的特点将电磁暂态计算中硬件设备的优点充分发挥出来[5-6],数据的并行处理极大提高了电磁暂态计算速度。而算法上的并行实现更是为电磁暂态计算效率的提高做出了卓越的贡献[7-9],得到了可观的加速比。

另一方面，大步长仿真也是提高电磁暂态仿真的重要手段。文献[10]成功实现了基于时间尺度变化下的大步长电磁暂态仿真；而动态相量的引入也带来更多电磁暂态大步长仿真的可能性[11-13]。动态相量建模法可以实现大步长仿真的本质是因为作了降频处理，使快变化变成慢变化，但动态相量也暴露出很多不足，动态相量对非线性元件建模依然复杂，并且动态相量将时域信号转变为复数信号，造成系数矩阵增维，也增加了计算量。总的说来，对动态相量的研究还有待增加。

电磁暂态计算中数值方法的选择也为大步长仿真提供了选择性。经典的隐式梯形法由于具有A稳定性，且拥有二阶计算精度，广泛应用在电磁暂态计算中。但隐式梯形法不具有L稳定性，即无法有效抑制突变情况下的振荡特性，且其仿真步长小，因此更多多级多阶的方法被应用于电磁暂态计算中[14-15]。其中微分求积法原理简单，易于实现。具有A稳定性且可以有效抑制震荡。文献[16]已经证明了微分求积法与龙格库塔(RK)方法的等值性，其计算结果为s级s阶精度。和隐式梯形法相比可以采取更大的仿真步长。但对于s级微分求积法来说随之而来的是内点的引入，由于需要在每个步长里引入s个内点，造成系数矩阵维数增加到原来的s倍，因此在矩阵求逆上会花费大量时间，使得大步长计算失去意义。文中算法在微分求积法的基础上，结合V变换的特点，根据增维后的矩阵特点进行分块求解，提高矩阵求逆的速度，以此来提高基于微分求积法的电磁暂态计算速度。

1 微分求积法简介

若函数f(x)在区间上光滑可导，则f(x)在网格点ci,i∈(1,s)上的导数可由该区间上所有网格点处的函数值的线性加权和表示，即：

(1)

式中gij为加权系数;s为整个区间进行划分的网格点数，不包括起始端点。将式(1)写为矩阵形式为:

f(1)(c)=G0f(c0)+Gf(c)

(2)

其中：

(3)

(4)

且：G0=-Ge，e为s维单位列向量。微分求积法加权系数矩阵G一般有两种求解方式，一种是将拉格朗日插值基函数作为试函数带入式(1)求解，叫显示表达式；另一种是将一般多项式函数带入式(1)求解，其结果由范德蒙德矩阵及其逆矩阵的乘积来表示，称为隐式表达式，其结果如下：

(5)

其中：

(6)

(7)

αs=[α1,α2,…,αs]T=(1/s)V-1cs

(8)

(9)

对于网格点的选取，常见的有勒让德网格、切比雪夫网格、均匀网格等，采取的是切比雪夫网格，其表达式为：

(10)

电磁暂态过程是由磁场和电场的变化引起电压、电流的变换过程，由于变换速度快，一般由一组带有初值的微分方程来表示：

(11)

式中x∈Rm×1，x为系统中状态变量的集合;g(t)只与时间变量有关;x0则为t0(t=0)时刻状态变量x的初值。

将积分区间[tn,tn+1]正则化到c∈(0,1)上，并将式(11)带入式(2)，可得：

(12)

(13)

令：A=G-1≡[aij]，⊗示直积计算，则可由下式来表示微分求积法求解步骤：

(14)

2 基于微分求积法的电磁暂态计算

将式(14)写为矩阵格式则可得：

(15)

式中：

(16)

式中Im为m维单位矩阵，利用A=G-1，将式(15)变换得：

(17)

当式(12)描述为非线性问题时，定义：

(18)

用牛顿迭代法对式(17)进行整体求解，ξ为迭代次数。带入式(18)定义的初值，则：

-JΔx(ξ)=∇R(x(ξ))

(19)

式中：

(20)

(21)

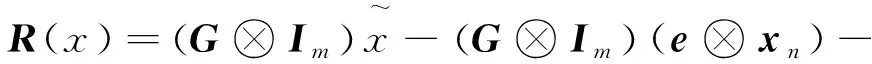
(22)

式中Is为s维单位阵。令：

(23)

带入式(5)，则式(19)变为：

(24)

式中：

(25)

(26)

(27)

式(19)可以写为：

(28)

如果直接求解式(28)，在每一次迭代中都会对增维矩阵(s×m维)进行三角分解，若m很大将会增加很大的计算量，使得微分求积法大步长的优势失去意义。观察式(28)，由于As矩阵具有特殊结构，因此其逆矩阵也具有特殊结构，表达式为：

(29)

将式(29)带入式(28)，并且展开分块可得：

(30)

(31)

令：

(32)

(33)

(34)

(35)

(36)

将式(32)～式(36)带入式(30)和式(31)可得：

(37)

观察可得，H2为下三角矩阵，因此只需要进行简单的前代运算就可以将式(37)第一式中的y2表示成y1的线性表达式，而不需要进行复杂的三角分解，即：

y2=φ(y1)

(38)

再将式(38)带入式(37)的第二式，得：

(39)

Q∈Rm×m，利用LU三角分解，解出y1，带入式(38)，解出y2，在通过式(23)反解出Δx即可。通过判断是否小于收敛精度，小于收敛精度则计算下一个步长，大于收敛精度，则需要按照内点平均值作为初值方式进行下一次迭代，直到收敛到精度范围内则开始进行下一个步长的计算。

当初值问题为线性时变微分方程时，即：

f(x)=Utx

(40)

Ut只与时间变量有关。将式(40)带入式(17)，则有：

(41)

式中：

(42)

G′(t)=(G⊗Im)(e⊗xn)+hG(t)

(43)

令：

(44)

做近似处理：

(45)

带入式(42)，则式(42)中对角矩阵块变为相等的矩阵块。式(41)变为：

(46)

(47)

将式(46)按照非线性部分算法处理，进行分块处理。即可获得可观的加速比。

3 算例仿真

上述算法是在微分求积法基础上提出来的，旨在解决由于内点引入，使得矩阵增维降低计算速度的问题。此部分中引入三个算例，分别为非线性和线性时变系统算例，并从精度和速度两个方面进行讨论，证明文中算法的有效性。算例仿真部分的算法都是在三级微分求积法上形成的。

3.1 加速比定义

定义文中算法仿真时间与其他算法仿真时间之比为加速比，加速比为仿真时间之比，没有量纲。具体规定为：加速比K1表示传统串行微分求积法与文中算法的仿真时间之比(步长一致)；加速比K2表示小步长隐式梯形法与文中算法的仿真时间之比；加速比K3表示小步长隐式梯形法与传统串行微分求积法的仿真时间之比。大步长与小步长在每个算例里均有具体的定义。

3.2 含非线性负荷的高压输电线路仿真

含非线性负荷的高压输电线路系统如图1所示。在系统合闸时，输电线路首端和末端将会产生过电压，需要评估过电压对输电线路电力设备绝缘的影响程度，为了提高过电压电磁暂态过程的数值计算效率，需要在更短的时间内得到其仿真结果。

图1 含非线性负荷的高压输电线路仿真图Fig.1 Simulation diagram of high voltage transmission line with nonlinear load

图1中，输电线路L首端与电源，电阻Rs，电感Ls串联，输电线路末端接有一非线性负载，由定电阻RL和非线性电感LL组合表示，LL中磁链φ与iL的数学关系为：φ=atanhbiL。输电线路全长100 km。其余参数如表1所示。

表1 参数表Tab.1 Parameter table

本算例中采用分段π模型电路对输电线路进行建模。每段电路模型如图2所示。

图2 π型等值电路Fig.2 π model equivalent circuit

本算例里将输电线路分为30段，每段输电线路的电磁暂态过程由式(48)表示：

(48)

仿真总时长为0.004 s，t=0时刻合闸。输电线路首端末端约束方程为：

(49)

将输电线路方程和首尾两端约束方程联立起来，最终含非线性负载的输电线路电磁暂态数学模型为：

(50)

式中x为系统状态变量；U为系统线性部分系数矩阵；f(x,t)为系统非线性部分。

分别用隐式梯形法、串行的微分求积法对式(50)进行离散，牛顿-拉夫逊迭代求解离散后的非线性方程组,再用文中算法对式(50)进行离散求解。隐式梯形法仿真步长1 μs(后文称为小步长)，串行的微分求积法以及文中算法仿真步长10 μs(后文称为大步长)。设置收敛精度为10-4，三种算法每个步长内只需要迭代两次就能完成收敛。

图3为采用文中算法仿真得出的输电线路首端和末端的电压，图4为文中算法(大步长)和隐式梯形法(小步长)仿真出的输电线路首端电压和末端电压波形的误差曲线。需要注意的是由于串行微分求积法和文中算法在离散方法和步长的选择上是一致的，两种算法的精度误差在10-5之内，故不再给出误差曲线。

由图3和图4可知，文中算法步长是隐式梯形法步长的10倍，但两者仿真精度误差如图4所示，说明微分求积法能在大步长仿真下依旧保持仿真精度。加速比以及计算时间以表2给出。

图3 输电线路首端末端电压Fig.3 Voltage at the front end of the transmission line

图4 文中算法和隐式梯形法精度误差图Fig.4 Algorithm proposed in this paper and the implicit trapezoidal method precision error graph

由于传统串行方式下，每一次迭代求解过程都会进行s×m维矩阵的LU分解，即使采用大步长计算，增维矩阵的三角分解也使得计算效率低下，反映为表2中的K3值，其加速比不明显。对于文中算法来说，在采用大步长的计算基础上，每一次迭代过程中都会将s×m维矩阵的三角分解转换为(s-1)×m维矩阵的前代运算以及一个m维矩阵的三角分解，且相对于传统串行微分求积法来说，这种加速优势将会随着一次又一次的迭代累积，最终形成可观的加速比，反映为表2中的K1、K2值。

表2 加速比及计算时间Tab.2 Acceleration ratio and calculation time

3.3 柔性高压直流系统算例

图5为柔性高压直流系统图(VSC-HVDC)，下标为1代表系统整流侧，下标为2代表系统逆变侧。对上述系统有两点假设：

图5 柔性高压直流系统图Fig.5 Flexible HVDC system diagram

(1)换流桥均由理想阀元件组成，即其正向漏电流为零；

(2)系统电压、电流满足三相平衡条件且为工频正弦波。

整流侧、逆变侧时域方程为：

(51)

直流侧时域方程为：

(52)

式中：

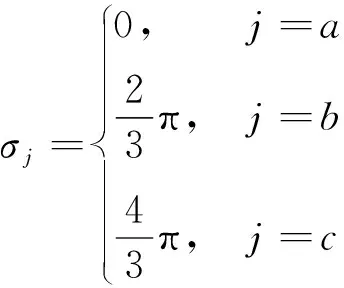
将式(51)和式(52)整合成矩阵形式方程：

(53)

式中:

VSC-HVDC系统参数：两端电压源电压分别为3 kV和2.8 kV,系统频率为50 Hz，两侧电气参数一致，即：

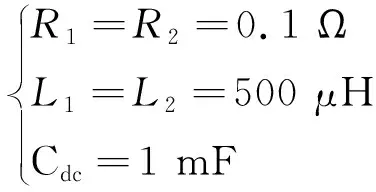
t=0.06 s时，VSC其中一侧调制比由0.78下降到0.65，t=0.12 s时恢复到初始值。总的仿真时长为0.3 s。

为了满足电网对实时仿真的要求，提高电磁暂态仿真速度是极其必要的。下面分别用隐式梯形法对式(53)进行离散仿真，步长为0.0001 s(小步长)；微分求积法对式(53)进行离散仿真，串行求解，仿真步长为0.001 s(大步长)；文中算法对式(53)离散仿真，步长为0.001 s(大步长)。图6给出了由文中算法仿真出来的直流电压波形图以及与小步长隐式梯形法仿真结果的精度误差曲线。由于微分求积法串行算法在离散算法和步长选择上与文中一致，两者之间的仿真误差在10-8之内，故不再给出其误差曲线。

图6 文中方法计算结果Fig.6 Calculation results of the proposed method

由图6可以看出，即使微分求积法仿真步长为隐式梯形法仿真步长的10倍，却依然可以达到很高的计算精度。加速比由表3示出。

表3 加速比及计算时间Tab.3 Acceleration ratio and calculation time

由表3可以看出：虽然相比隐式梯形法，微分求积法增大了仿真步长，但由于每个步长引入s个内点使得计算量增加，因此微分求积法串行方式下其加速比K3只是略大于1，即加速优势不明显，而文中算法在采用大步长的前提下，针对引入内点增加计算量这点提出改进方法，在每一个计算步长里将s×m维矩阵的求逆计算分解为(s-1)×m维矩阵的前代运算和m维矩阵的三角分解，减少计算量，得到了较为可观的加速比。

3.4 VFTO算例仿真

气体绝缘开关设备中的隔离开关投切空载短母线时会产生特快速暂态过电压(VFTO)，具有频率，幅值，陡度高的特点，对与其相连设备造成安全威胁。为了给保护整定提供电气参考值，维护设备正常运行，对VFTO进行高效率电磁暂态仿真是必要的。图7是一个简化的VFTO计算模型。

图7 VFTO系统图Fig.7 VFTO system diagram

图7中，电源电压幅值为550 kV，LT，CT组合表示变压器等效电感和对地电容，L1，L2为连接短母线，由无损短传输线表示，L1长度为10 m，L2长度为3.5 m。CR表示隔离开关对地电容。隔离开关合闸过程的电弧模型由以下数学表达式来模拟：

R(t)=R1e-t/τ1+R2e-t/τ2

(54)

无损传输线单位长度的电感和对地电容分别由L0，C0表示。所有参数值由表4提供。

表4 参数表Tab.4 Parameter table

隔离开关投切空载短母线时，短母线上的残余电荷电压对VFTO有重要影响。考虑最严重的VFTO，即电源侧与残余电荷电压差达到2.0 p.u.(电源侧为1.0 p.u.,负荷侧残余电荷电压取-1.0 p.u.)。

输电线路采用分段π型等值电路，L1均分为20段，L2均分为7段。仿真时长为1.2 μs。VFTO数学模型表达式为：

(55)

Ut∈R57×57,且为时变系数矩阵，分别用隐式梯形法(步长为0.1 ns，小步长)，文中算法(步长为0.6 ns,大步长)，传统的串行微分求积法(步长为0.6 ns)进行离散仿真。仿真结果如图8所示，u(t)表示用隐式梯形法仿真出来的母线末端电压，v(t)表示由文中算法仿真出来的末端电压，Δuv(t)表示两者之间的精度误差。需要说明的是，由于文中算法和串行微分求积法所采用的离散方法和步长都是一致的，两者之间的计算精度误差在10-8之内，故不再给出误差曲线。

图8 VFTO结果对比图Fig.8 VFTO result comparison diagram

由图8可以看出，微分求积法采用大步长计算，其仿真结果依然保持一定精度。

加速比及计算时间在表5中给出。

表5 加速比及计算时间Tab.5 Acceleration ratio and calculation time

Ut为时变系数矩阵，对于每一个步长来说，Ut依然为定系数矩阵。因此每一个步长的计算都需要求解s×m维矩阵的逆。文中算法依旧将s×m维矩阵的求逆计算分解为(s-1)×m维矩阵的前代运算和m维矩阵的三角分解，因此会得到可观的加速比。

3.5 结果分析

通过上述三个算例的分析，可以发现，文中算法对非线性和线性时变系统是有明显加速效果的，其加速比是通过每次迭代或者是每个步长的快速求逆累积得到的。对于非线性电力系统算例来讲，s的取值不会影响非线性部分算法的迭代次数。所以无论是文中算法，串行微分求积法，还是隐式梯形法，每个步长的迭代次数均为两次。3.3节以及3.4节给出了两个线性时变算例，虽然都获得了较好的加速效果，但从这两个算例可以看出，矩阵规模越大其加速效果是更加明显的。而对于线性常微分算例来讲，由于系数矩阵为定常数矩阵，整个计算仿真过程只需要进行一次求逆计算。只需要不断更新初值和时间函数变量。加速优势无法通过累积得到，因此文中算法对此类算例效果不明显。

需要说明的是：针对非线性电力系统，无论其拓扑结构复杂程度如何，其电磁暂态过程最终可写为式(50)的形式；而对于线性时变系统来说，其电磁暂态过程可描述为式(53)的形式，利用所提算法对式(50)或式(53)进行离散仿真，便可以在保证精度的前提下得到可观的加速比。因此所提算法针对不同拓扑结构的非线性系统以及线性时变系统均具有有效性。

4 结束语

文中算法是在微分求积法基础上形成的，利用微分求积法V变换的特点，对增维矩阵进行分块处理，避免直接对增维矩阵进行三角分解，使得需要三角分解的矩阵由串行模式下的s×m维降低到m维，因此大大提高了基于微分求积法的电磁暂态计算速度。且算例表明，所提算法对非线性算例以及线性时变算例均有理想的加速效果，且矩阵规模越大其加速效果更加明显。文中算法可以基于任何级的微分求积法。因此，文中算法可以有效提高基于微分求积法的电磁暂态仿真效率。