基于变分模态分解和深度学习的短期电力负荷预测模型

阳曾，丁施尹，叶萌，李晶，薛书倩，吴昊天

(1.广东电网有限责任公司广州供电局电力调度控制中心，广州 510000； 2.北京清软创新科技股份有限公司，北京 100085； 3.华北电力大学，北京 102206)

0 引 言

负荷预测是制定电力供应计划和电网电量供需平衡的关键挑战之一，它是电力市场运营的基础工作和电力规划中不可或缺的组成部分[1]。电力系统负荷预测可根据预测的时间长短分为超短期、短期、中期和长期预测[2]。其中，短期负荷预测是电力日常调度工作中重要的一项内容，同时是能量管理系统的重要组成部分。提高短期负荷预测的准确性，有助于提高电力设备的利用率，降低能耗，缓解能源的供应端和需求端两者之间的不平衡[3-4]。

现阶段，围绕负荷序的时序性和非线性特点，短期负荷预测方法层出不穷，有多元线性回归法[5]，其优点在于结构形式简单，预测速度快，但描述较复杂的问题时，精度较低；卡尔曼滤波法[6]，该算法能很好的解决数据中的噪声问题，但这样也会造成变化较大的负荷也被筛选出去,对预测结果造成一定的影响；灰色理论法[7]，该方法所需数据量少，计算方便，但未考虑到相关因素之间的联系，故误差偏大；支持向量机[8]，其泛化能力好，预测精度较高，预测但运算时间太长，难以预测大规模数据；随机森林法[9]，可以处理高维数据，其泛化误差小，但对于噪声较大的数据，易出现过拟合现象；以及应用较为广泛的神经网络法[10-11]等。随着深度学习的兴起与发展，多种深度学习神经网络逐渐应用于负荷预测领域。文[11]利用LSTM网络预测负荷功率, 在浅神经网络中，只能改变单隐层神经元的数量，而在LSTM网络中，宽度和深度都可以改变，它通过预训练方式缓解了传统网络局部最优点问题。

对于随机性、波动性较强负荷序列而言，单一预测方法难以得到理想的预测精度。目前，各种组合预测方法广泛应用在短期负荷预测领域，以EMD[12]为主的分解方法能有效的实现原始负荷序列的分解，实现平稳序列和非平稳序列互相分离的目的，然后再结合预测方法对各个IMF分别进行预测。但是，EMD分解方法难以避免模态混叠现象产生，得到的虚假IMF，会对预测精度产生不利影响。文[13]采用VMD将负荷数据分解为特征互异的模态函数，避免了模态混叠现象发生，提升了信号的分析效果。

基于以上研究工作，文中以某地区负荷数据为研究对象，对负荷序列进行VMD分解，获得多个特征互异的子序列，并分别结合LSTM网络进行预测，将多个预测结果叠加后得到最终的预测结果。与单一LSTM和EMD-LSTM方法预测结果相比，验证了所提方法可有效挖掘负荷序列潜在特征，从而提升预测精度。

1 VMD算法原理

2014年Konstantin Dragomiretskiy提出一种新型的VMD估计方法，用于非平稳信号的自适应分解，可将复杂的信号分解成K个调频调幅的子信号[14]。它本质上是一个自适应维纳滤波器组，可以有效地将测试信号分解成一组有限带宽的中心频率。不同于EMD和EEMD方法，VMD方法采用了非递归及变分模态求解模式处理原始信号，具有较好的抗噪声性能和非平稳性能信号处理效果。

VMD的目的是将多分量信号分解为带宽上具有特定稀疏性的有限带宽模式的集合；相反，这些分解的模式也能够重构输入信号。求解约束变分优化问题：

(1)

式中uk(t)为输入信号的模态函数；{uk}表示模态集合{u1,u2, ……,uk}；wk是对应于输入信号的第k阶模态的中心频率；{wk}表示分解后的模态对应的一组中心频率{w1,w2, ……,wk}；f(t)是输入信号；δ(t)是单位脉冲函数。

将拉格朗日乘子λ和二次惩罚因子α引入，可以将式(1)改写为：

(2)

使用乘法算法的交替方向法求解(2)，获得一组模态分量及其各自的中心频率。每个模态可由频域中的解估算出来，表示为：

(3)

在式(3)中具有维纳滤波结构的特点，它直接更新了傅立叶域中的模态。此外，还可以通过提取滤波分析信号傅里叶逆变换的实部，在时域内得到这些模态。

(4)

2 LSTM神经网络结构

传统的神经网络在处理分类以及回归问题时难以避免会陷入局部最优点，而深度学习神经网络通过预训练方式缓解了这个问题[15]。LSTM网络源自于循环神经网络的一种，而后者在每个时刻都对应着一个输出，同时结合其当前时刻的状态得到对应的输出。当前的状态是根据上一时刻的状态以及此刻的输入共同作用来决定的，通过这种结构比较适合解决与时间序列有关的问题。但是，如果时间序列过长会导致当前时刻节点对历史时刻节点的感知能力不足，从而出现梯度消失的问题。而且当前时刻预测和当前时刻所需信的息之间的跨度长短不一致，这种长期依赖的问题是传统的循环神经网络所不能解决的。

LSTM网络对经典循环神经网络做了改进，通过引入“遗忘门”，让信息有选择性地影响RNN中每个时刻的状态。计算节点由输入门、输出门、遗忘门和cell组成[16]，LSTM的计算节点图见图1。

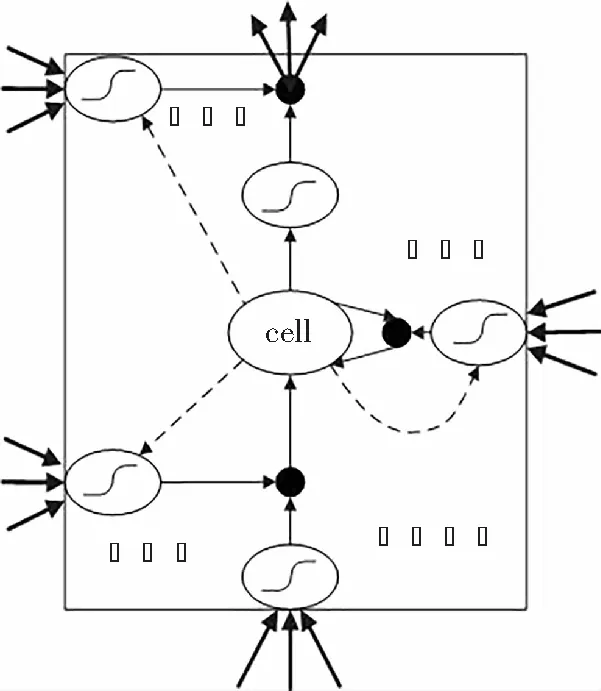
图1 LSTM模型结构Fig.1 LSTM model structure

在图1中，cell为计算节点的核心，记录着当前时刻的状态；控制信息的输入和输出则分别由输入门、输出门操控；而遗忘门则控制着细胞历史时刻状态信息的储存。遗忘门的输出值始终保持在[0, 1]之间，这得益于门利用的sigmoid激活函数，输出值为0，将上一状态的信息全部丢弃，输出值为1，上一状态的信息则全部保存。如式(5)所示：

ft=σ(Wf·[ht-1,xt]+bf)

(5)

式中Wf是遗忘门的权重矩阵；bf是偏置项；[ht-1,xt]是遗忘门的输入向量；σ是sigmoid函数。

“输入门”负责新状态的补充，根据xt，ht-1来判断ct-1状态中的哪些部分应当写入当前时刻状态ct中去，如下：

it=σ(Wi·[ht-1,xt]+bi)

(6)

式中Wi是输入门的权重矩阵；bi是输入门的偏置项。

同时，新状态的候选值c*t由tanh函数产生，c*t可能会加入到新状态中，如下：

(7)

那么当前时刻的状态ct就是由上一时刻的状态ct-1乘以遗忘门ft，再用新状态候选值c*t乘以输入门it，再将两个乘积求和，有：

(8)

类似地，输出门表示如式(9)所示：

ot=σ(Wo·[ht-1,xt]+bo)

(9)

式中Wo是输入门的权重矩阵；bo是输入门的偏置项。而LSTM最终的输出ht是由输出门与单元状态共同决定的。

ht=ot·tanh(ct)

(10)

在网络传播的过程中，ot并不是唯一起作用的，ht才是LSTM网络的特殊之处，它是根据三个门新增加的，有效解决了梯度消失的问题。

3 VMD-LSTM模型的短期负荷预测

电力负荷基于用户习惯性消费信息，受人类活动、气象条件、社会经济和政治因素等不同程度的影响表现出一定的波动性、随机性的特点。然而，人类生活生产活动有一定的规律性，因此，负荷也具有较强的周期特性。负荷序列本质上具有不稳性，为精细研究分析负荷序列特点，采用VMD方法对原始负荷序列进行分解，得到一系列有利于预测的负荷分量。由于深度学习算法具有多层次内部结构和重复学习特征的训练方式的特点，所以能更好地应对负荷预测问题，所以将各个负荷分量结合LSTM网络进行训练预测，叠加每个分量预测结果，进而得到了VMD-LSTM模型的最终预测结果，模型框图如图2所示。

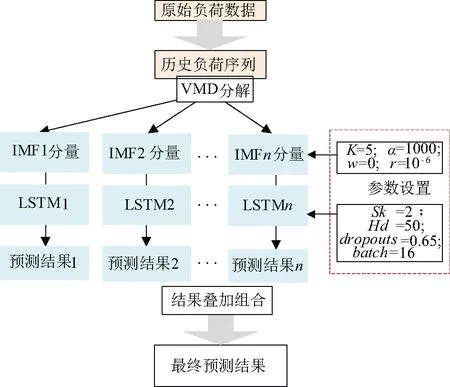
图2 负荷预测模型Fig.2 Load forecasting model

图2中给出了VMD的参数设置[14]：通过反复实验测试，模态函数个数K=5；二次惩罚因子α=1 000；收敛判据r=10-6。起始中心频率w=0。LSTM网络参数调试，通过调节LSTM网络中的堆叠层数、隐含层神经元个数、Dropout参数以及每批处理样本数量来提升网络的预测的性能。

(1)堆叠层数(Sk)和隐含层神经元个数(Hd)

堆叠层数及隐含层神经元个数的选取对负荷预测精度有着显著的影响，以日周期分量数据为测试对象，计算了当堆叠层数分别为1层～3层，隐含层神经元个数分别为5、20、50、100个时训练集和测试集的MAPE，结果见表1所示。

表1 训练集及测试集的测试结果Tab.1 Test results of training set and test set

从表1中，可以看出当网络堆叠层数为2，隐含层神经元个数为50时训练集和测试集的MAPE最小，故以此网络参数进行后续的短期负荷预测仿真实验。

(2)dropout参数

dropout参数的设置可以有效抑制神经网络训练的过拟合。dropout的原理是在模型训练时，以一定的概率让某个神经元失活。目前学术界对dropout的取值方法并无定论，具体到本文模型，采用遍历的方法，通过计算平均准确度(mean Accuracy, mAcc)选取最优值，如式(11)所示:

(11)

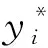
本文尝试了10种不同的dropout比例，实验结果如图3所示，当dropout参数从0.5增大至0.95，mAcc呈现了先增加后减小的变化趋势，在dropout取0.65时mAcc获得最大值95.83%。

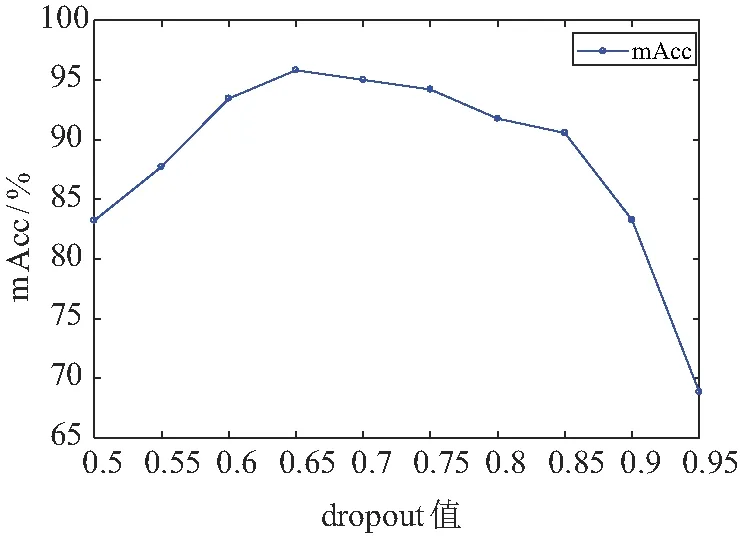
图3 不同dropout参数下负荷预测mAccFig.3 mAcc of load forecasting with different dropout parameters

(3)每批处理样本数量(batch)

在LSTM网络中每批处理样本数量如果值太小，则很容易不收敛；如果取值过大，容易陷入局部最优解。本文选取的方法是以128为分界线，向上乘2，向下乘0.5，训练后比较测试结果，测试结果显示向下更好，向下继续乘0.5，直到结果不再提升为止，最终测试结果该参数值取16。

4 实验分析

实验采用某地区2019-06-16至2019-06-30之间的负荷数据，采样间隔15 min，共计采样点1 440个，以前面12天的数据作为训练样本，后面3天的数据作为测试样本。原始数据集分别由EMD和VMD方法进行分解，原始负荷序列及分解结果分别见图4～图6。

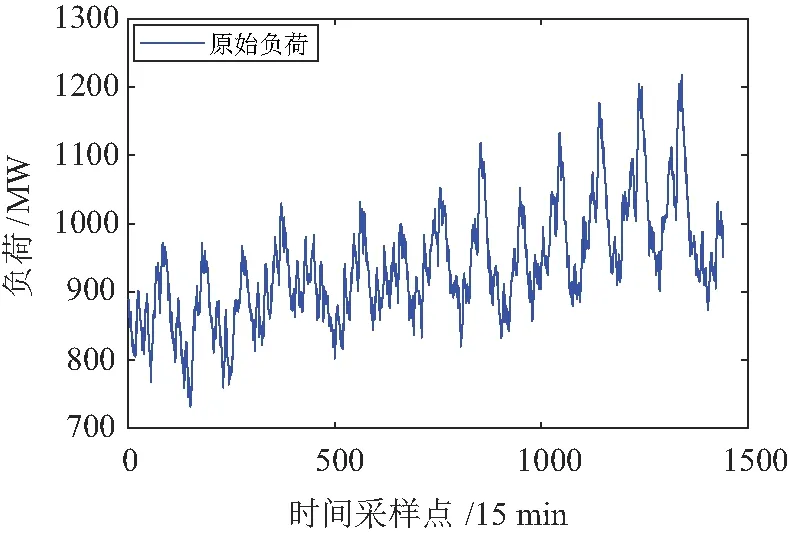
图4 原始负荷序列Fig.4 Original load sequence

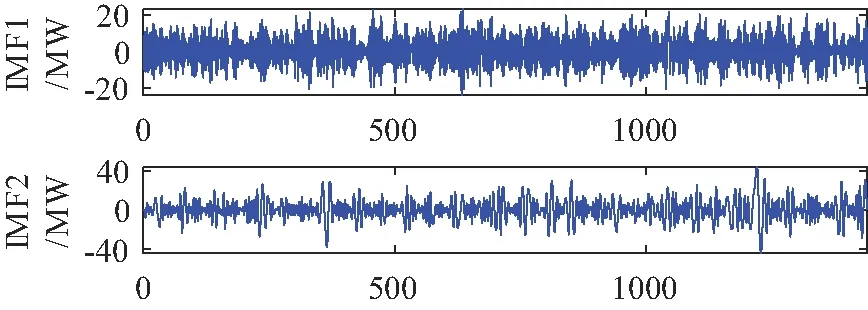
图5 EMD分解结果Fig.5 EMD decomposition results

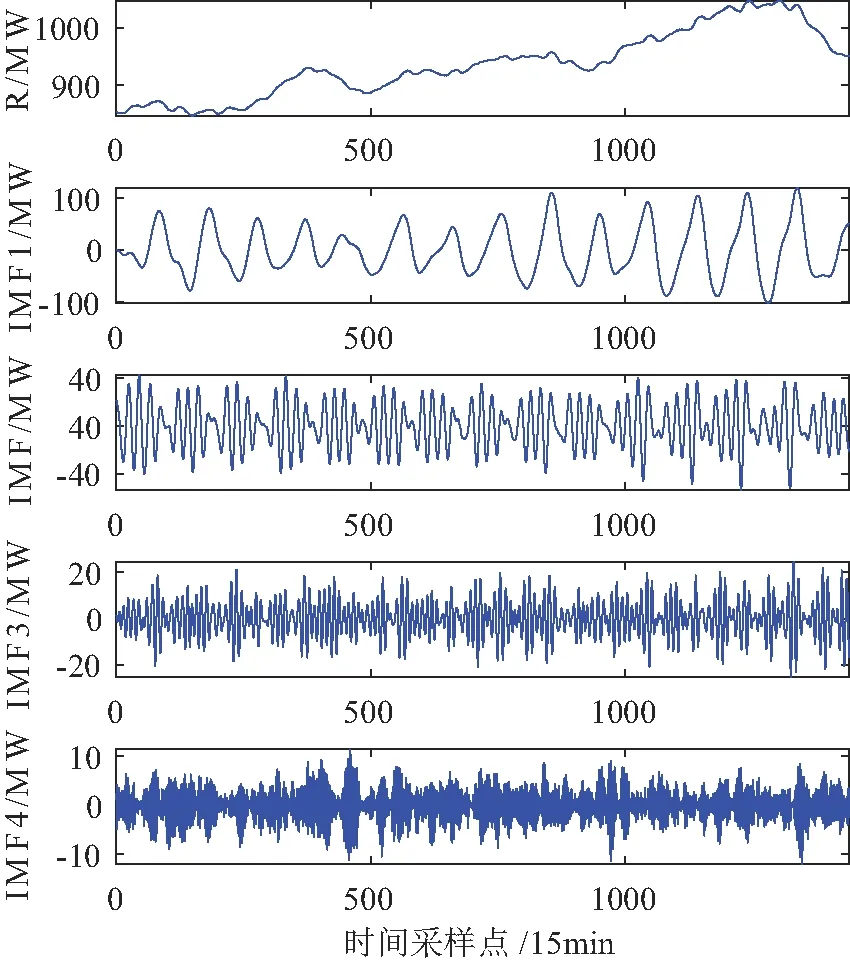
图6 VMD分解结果Fig.6 VMD decomposition results

从图4中可以看出，原始负荷序列的波动性较强，从图5和图6的分解结果可以看出，由EMD分解方法的模态分量多达8个，而VMD分解出来的模态分量只有5个，这大大减少了预测的计算规模；高频分量不以利于预测，可以看出VMD分解出来的高频分量幅值占比更少，有利于减少预测误差；中低频部分VMD分解的分量的规律性则明显比EMD分解的分量规律性要强；两者分解出来的低频部分都较为平缓，可以看出VMD分解出的低频分量更接近原始负荷序列的波动趋势。因此，从两者分解结果来看VMD方法更有利于后续建模预测。

接着根据上一节LSTM网络测试的参数，利用LSTM网络分别对原始负荷数据、EMD及VMD分解的分量序列进行预测，并分别叠加后两种方法的预测结果，得到EMD-LSTM方法和VMD-LSTM方法的最终预测结果。图7中给出了三种方法的预测结果曲线。

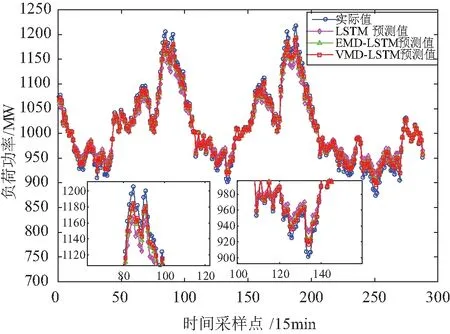
图7 三种方法的预测结果比较Fig.7 Comparison of prediction results of the three methods

科学和全面的指标在对各种负荷预测模型的筛选和纠正中发挥着重要作用。目前评价负荷预测结果的指标众多，通常是采用平均绝对百分误差(Mean Absolute Percentage Error, MAPE)来评估模型优劣，采用均方根误差(Root Mean Square Error, RMSE)来反映预测的精密度，两者数值越小，模型的预测效果越好[17-19]。三种方法的误差统计结果见表2。

(12)

(13)

式中各符号的意义同式(11)。

图7中的放大区域中可以看出单一采用LSTM方法在负荷峰谷值部分预测误差很大，而VMD-LSTM方法略优于EMD-LSTM方法，预测结果比较理想。在表2中，从预测日的平均值角度分析，VMD-LSTM方法的具有最好的预测精度，MAPE为0.62%，RMSE为7.91 MW，验证了该方法具有较好的预测性能。

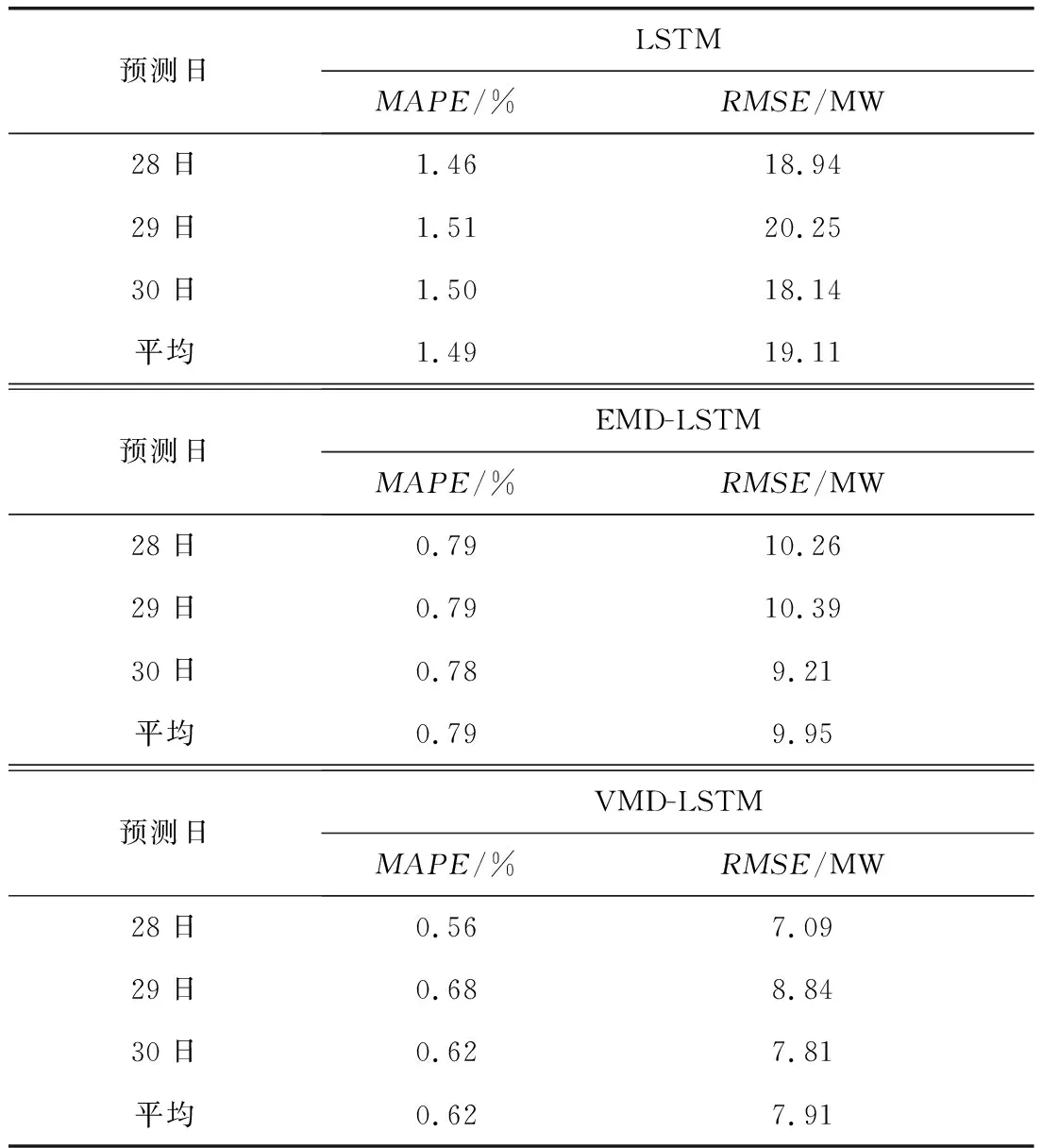
表2 三种方法的误差统计结果Tab.2 Error statistics results of the three methods

5 结束语

文章提出了一种基于VMD-LSTM的短期负荷预测方法。实验验证，在波动性较强的负荷序列中，VMD可有效提取其内在具有紧支撑傅里叶频谱特性的负荷分量。对比EMD方法，VMD方法具有可手动调节模态分量个数的优势，进而可减少预测的计算规模。同时，考虑到LSTM具有预训练方式的特点，可有效缓解传统神经网络易陷入局部最优点问题，可为高精度预测结果提供强力保障。对比LSTM和EMD-LSTM方法，突显了本文方法优越的预测性能，为研究短期负荷预测提供一定的参考意义。

在后续的研究中，可以考虑在输入数据中加入影响负荷变化的特征，比如气象条件、经济因素等；可考虑结合优化算法，对LSTM的权值和阈值进行逐层优化，以达到提升预测精度的目的。