基于多能源需求响应的综合能源系统动态优化控制研究

张娜，王欢，宋坤，程孟增，张明理，叶鹏

(1.辽宁省电力有限公司经济技术研究院， 沈阳 110015； 2.沈阳工程学院 电力学院， 沈阳 110136)

0 引 言

能源问题是支撑人类社会可持续发展的核心问题，伴随着风、光等可再生能源技术的迅猛发展，源端与荷端的能源多样化促使能源系统进一步耦合，打破原有各能源供用系统单独规划、单独设计和独立运行的既有模式，综合能源系统(Integrated Energy System，IES)应运而生[1-3]。

IES是以电力为核心，融合燃气、热力等多种能源，以实现能源高效利用与可再生能源消纳为目的，有机协同能源生产、输配、利用等环节的一体化能源服务系统，其供能子系统的高度耦合，可以有效减少化石能源消耗，实现社会用能效率最优，是构建未来低碳生活的重要途径[4-6]。在综合能源的网络架构下，IDR利用电能、天然气等不同能源间的耦合特性，通过削减、转移用能负荷来参与DR，并可兼顾用户的满意度与舒适度[7-8]。与DR相比，在不同价格方案下，实施IDR的效果明显不同，其削峰填谷效果更明显、用户满意度与舒适度更高[9-11]。

目前国内外学者针对DR在IES中的应用展开了大量研究。文献[12]建立了电价激励型需求响应(PBDR)总规划成本碳排放最小的双目标优化模型，对计及DR计划的区域IES容量配置的经济、环境效益进行了综合评估分析，并应用价格需求弹性系数进行用电负荷曲线修正；文献[13]针对面向DR的储能设备控制问题，基于模型预测控制，建立了相应的储能需求关系模型，利用遗传算法提出了控制优化的求解方法；文献[14]研究了园区IES在考虑DR时的运行优化调控，构建了园区IES的整体框架，并确定了能源供应商、园区运营商、园区用户主从博弈的分析方法；文献[15]提出一种考虑DR及动态天然气潮流的“电-气”IES优化调度新模型；文献[16]建立了包含风电、光伏、燃气轮机以及电热负荷等构成的热电联供园区微网模型。综上所述，IDS作为一个最新的概念，其研究成果还未形成完整的体系，建模较为粗糙，缺少精细化的建模描述，对用户侧的可调资源挖掘不够，应用场景较单一。

文中提出考虑多能源需求响应下的综合能源系统动态优化控制方法。依据电力需求和价格弹性理论，综合考虑了能源价格对电力、天然气等能源消耗量的影响，构建了多元化用能价格需求响应模型；以经济和环境成本最小为目标，建立了基于DR机制的IES多目标动态运行优化模型，并采用HP-NSGA-Ⅱ算法进行求解，为推动综合能源互联网向有利于促进分布式新能源消纳的方向发展提供了有效参考依据。

1 IES的结构

IES不同子系统间存在密切的互补和转换关系，子系统间能否有效配合将直接影响系统效率，同时不同的负荷需求和用能选择也将直接影响调度结果。根据已有研究，IES的结构如图1所示[17-18]。

图1 IES的结构框图Fig.1 System structure block diagram of IES

因分布式电源受地理条件限制明显，实际中的IES多数是以冷热电联供系统(CCHP) 为核心的。CCHP利用燃气轮机或内燃机发电，利用换热器供热、吸收式制冷机供冷，负责用户的冷、热、电负荷。联合运行效率高达 85%，是现今IES中最具潜力及发展前景的运营模式。

2 多元化用能价格需求响应模型

ID与电价密切相关，当电价上涨或可靠性受到威胁时，用户在收到ID信号后，可改变用电模式，调整用电行为，实现资源的优化配置[18]。

在电价弹性理论中，ID价格弹性反应不同时期能源消费对价格的敏感度，它是一定时期负载变化率与价格变比率的比值，其关系如式(1)所示：

(1)

式中βii为i时间段的自弹性系数;ΔQi为i时间段内负载变化量；Δpi为i时间段内能源价格的变化量；Qi、Qi0分别表示i时间段内原始负荷和峰谷分时能源价格实施后的负荷量；pi0、pi分别为i时间段内的原始价格和峰谷分时能源价格实施后的峰、谷分时价格。

i时间段的负荷随j时价格的变化交叉弹性系数βii为:

(2)

式中Δpj为j时能源价格变化量；pj0为j时价格；pj为j时峰谷价格。

假设能量需求为线性函数，根据原始能源价格、峰谷分时价格、原始负荷和价格需求弹性，可以获得实施需求响应后各个时间段的能耗。

为了最大化用户的利益，假设：

(3)

则有

(4)

经济学中常引用的效益函数如下：

(5)

(6)

能量需求和能量价格之间的关系为：

(7)

由于IES内部耦合多个冷、热、电负荷需求，且不同负荷相互影响，所以需要构建多元化的综合型价格需求响应模型。以电力负荷和天然气负荷之间耦合关系为例进行建模分析，两者需求响应模型分别为：

(8)

(9)

式中，QE，i0为需求响应前的电负荷；QE，i为需求响应后的电负荷；QN，i0为需求响应前的天燃气负荷；QN，i为需求响应后的天然气负荷；γel，i为需求响应电价；γg为固定电价；∂fl，i为需求响应天然气价格；∂f为固定天然气价格。

电力负荷和天然气负荷的消减范围为：

(10)

(11)

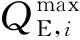
多元化用能价格需求响应模型如下：

(12)

根据上述多能源价格需求响应模型，用户可以在不同时间节点上选择不同种类能源进行替代，选择不同形式的能源输出方式进行供能。

3 综合能源系统中各元件数学模型

3.1 CCHP机组

CCHP系统数学模型如下：

(13)

(14)

(15)

HCCHP=HWHB-UCCHP

(16)

CCHP机组输出冷功率是由燃气轮机余热经由吸收式制冷机转化产生的，因此输出冷功率需小于余热锅炉输出热功率。

HWHB≥UCCHP

(17)

3.2 电转气设备

GP2G≥ηP2GPP2G

(18)

式中GP2G为电转气设备生产的天然气总量；PP2G为需要消纳的风电和光伏发电的功率；ηP2G为电气转化效率。

约束条件为：

(19)

3.3 电锅炉模型

HEB=ηEBPEB

(20)

式中HEB为电锅炉的供热功率；ηEB为电锅炉的供热效率；PEB为电锅炉消耗的电功率。

约束条件为：

(21)

3.4 电制冷机模型

UER=PERCOPER

(22)

式中UER为电制冷机的供冷功率；PER为电制冷机消耗的电功率；COPER为电制冷机的能效系数，取值3.2。

约束条件为：

(23)

3.5 光伏发电系统模型

(24)

式中PV为光伏发电功率；fV为光伏系统的功率降额因数，表示实际输出功率与额定条件下输出功率的比值，取 0.9；YV为光伏阵列容量；IT为地表水平面光照度；IS为标准测试条件下的光照度；αP为功率温度系数；TC为当前光伏电池表面温度；TCS为标准测试条件下的光伏电池温度，取 25 ℃。

约束条件为：

(25)

3.6 风机模型

(26)

式中PWT为风机功率；v为风机轮毂高度处的实际风速；vi、vo分别为切入、切出风速，当实际风速低于切入风速或高于切出风速时，风机不工作；P(v)为正常风速范围内的风机出力，由风速与功率特性曲线插值得到。

约束条件为：

(27)

3.7 储能电池模型

综合能源系统中电储能可以起到削峰填谷的作用，进而消纳更多富裕的光伏发电量和风电量，其储能容量和充放电功率关系模型可表示为：

(28)

约束条件为：

(29)

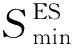
4 综合能源系统动态优化控制模型

4.1 目标函数

多源化能源供应模式下，基于DR的IES运行优化问题是一个典型的多目标优化问题，涉及非线性、随机性、离散性和不确定性等[19-20]。

为了实现IES总运行费用最低、污染物减排率、系统可靠性最高，需要采用多目标、多约束的运行模型进行求解，求解过程中考虑了经济和环境双重目标，其函数表达式为：

F(t)=min([fc(t)，fe(t)]t)

(30)

式中fc、fe分别为经济目标和环境目标；t为时间变量。

经济成本主要考虑购电成本、设备运行维护成本、燃料成本，蓄电池折旧成本等，针对光伏、风机、蓄电池和发电机构成的多能源网络，用下式表示为：

fc(t)=CE(t)+CH(t)+CU(t)+CG(t)

(31)

式中GE(t)、GH(t)、GU(t)、Ggas,max分别为电力Ggas,max、热力、供冷、供气子系统的运行成本。

电力系统的总成本由风、光清洁能源机组、CCHP 机组、储电设备等的外部主网购电成本、初始建设成本折旧额、运维成本及机组启停成本组成，用下式表示：

CE(t)=CB/E(t)+CC/E(t)+CM/E(t)+CS/E(t)

(32)

CB/E(t)=PBUY(t)·PE(t)

(33)

(34)

(35)

(36)

式中N为设备数；PE为外部主网售电价格；CC，n、Cλ，n、Vn、Tn分别为第n台设备的单位容量初始投资成本、容量、寿命、残值；Cn、Pn为单位出力的运维成本系数、发电量；CSS，n为启停成本系数；Un为设备的启停状态。

热力系统的总成本为：

CH(t)=CB/H(t)+CC/H(t)+CM/H(t)+CS/H(t)

(37)

供冷系统的总成本为：

CU(t)=CC/U(t)+CM/U(t)+CS/U(t)

(38)

供气系统的总成本为：

CG(t)=CB/G(t)+CC/G(t)+CM/G(t)+CS/G(t)

(39)

式中CC/G中考虑了P2G设备的影响。

环境成本主要考虑碳排放、其他污染气体及颗粒物排放对环境的影响，下式反映了不同污染排放物的环境影响差异：

(40)

式中Ve，i、Qi、Vi分别为第i项污染物的环境价值、污染物的排放量和污染物所受罚款；n为污染物种类。

4.2 约束条件

IES是一种多能源协调规划的能源供需系统，其电、气、热、冷四种能源的守恒关系为：

(41)

Ggas+GP2G=GCCHP+Gload

(42)

HCCHP+HEB=Hload

(43)

UCCHP+UER=Uload

(44)

式中Pgrid、Ggas分别为系统从大电网购买的功率和从天然气网购买的天然气量。Pload、Gload、Hload和Uload分别为电、气、热、冷四种负荷需求。

外部电能和天然气购买约束：

0≤Pgrid≤Pgrid，max

(45)

0≤Ggas≤Ggas，max

(46)

式中Pgrid,max和Ggas,max分别表示系统从外部购买电能和天然气的上限。

4.3 求解流程

由于优化模型存在多个变量、目标函数较为复杂，为了综合考虑IES中的能量需求、模型特征及每个能源供应单元中的输出功率，以往研究中，主要采用非劣性遗传算法NAGA-Ⅱ进行求解，其流程图如图2所示。

图2 NAGA-Ⅱ算法流程图Fig.2 Flow chart of NAGA-Ⅱ algorithm

NSGA-Ⅱ采用拥挤距离法及精英策略进行排序，有效保证了种群的多样性，在降低计算复杂度的同时加速了Pareto前沿收敛，但其在求解超过2个目标函数的多目标问题时，计算效率较低，且容易陷入局部最优。

针对上述问题，本文引入超平面投影 HP(Hyperplane Projection)的方法，在NSGA-Ⅱ的种群进化过程中，通过构建超平面，将种群投影到单位超平面上，进而平衡解集的收敛性与分布性。HP-NSGA-Ⅱ与NSGA-Ⅱ的不同之处在于父代种群的选择机制，其求解步骤为：

(1)输入原始数据，包括 IES各供能储能设备参数、综合需求响应相关参数、约束条件及典型日负荷曲线等；设种群规模为80，最大迭代次数为50，交叉概率为0.75，变异概率为0.25，Pareto最优个体系数为0.5;

(2)形成初始种群，对各设备出力情况进行编码，构成设备出力集;

(3)根据HP 对种群进行选择，并通过NSGA-Ⅱ的交叉和变异机制形成新子代种群，该过程中，各个体的每个维度需满足约束条件;

(4)判断是否达到最大迭代次数，若达到则可生成Pareto前沿解，否则继续执行上面步骤;

(5)使用 TOPSIS 法从 Pareto 前沿中寻得最理想解，得到最优方案。

5 算例分析

以典型的工业园区综合能源系统为例进行仿真分析。园区现有能源供应系统主要包括风力发电机组、光伏发电机组、储能设备、CCHP系统，电转气设备、电锅炉设备、电制冷设备和储气设备，其中CCHP系统中燃气锅炉排出的烟气将全部供给余热锅炉。表1为各设备运行参数。表2为不同能源污染物排放量、环境成本参数。图3为供电、供气、供冷和供热价格。

表1 设备运行参数Tab.1 Equipment operation parameters

表2 不同能源污染气体排放量、环境成本参数Tab.2 Pollution gas emissions and environmental cost

图3 电、气、冷和热的价格Fig.3 Prices of electricity, gas, cool and heat

结合发电模型与实际负荷，考虑园区自然条件，预测典型日电、热、冷负荷需求，如图4所示。典型日(24 h)供电量如图5所示。

图4 典型日热和电负荷需求Fig.4 Demand of typical daily heating and electric load

图5 典型日供电量Fig.5 Typical daily power supply

5.1 动态优化控制求解

通过价格需求响应模型中式(1)～式(3)，得到园区用户需求响应前、后的电、气、热价格对照如图6所示。随着电、气、热价的改变，需求响应前、后，电、热负荷也发生变化。图7为需求响应电、热负荷变化情况。在需求响应模型的基础上，可以得到电、热需求响应前后的负荷特性，如表3所示。

图6 需求响应前后电、气、热价格对照Fig.6 Comparison of electricity, gas and thermal prices before and after demand response

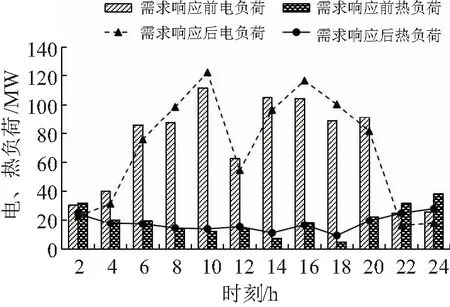
图7 需求响应前后的电、热负荷对照Fig.7 Comparison of electric and thermal load before and after demand response

表3 IDR前、后系统负荷特性Tab.3 Load characteristics before and after IDR

结合图6、图7和表3可知，需求响应前，电力负荷峰值为122.1 MW，负荷谷值为12.6 MW，受电价改变的影响，需求响应后峰值为111.3 1MW，谷值为20.5 MW，需求响应峰谷电力差由原来的109.4 MW降至90.7 MW，降幅约为28.5%。在电价高峰期，系统的功耗明显降低。

同时，对于热负荷，在20 h～6 h，负荷增加约2.3 MW至4.1 MW，其他时间段均有降低，大部分时间段降低约3.7 MW。除了受热价变化的影响，造成这些变化的主要原因是系统中的热能主要由CCHP提供，当电能波动较大时，CCHP机组的运行状态发生改变，并引起热负荷曲线发生变化。

由上述分析可知，价格型需求响应的实施，可以影响用户的负荷需求，有效提升系统内部功能，降低用户负荷峰谷差及系统用电高峰期负荷。同时，需求响应后的负荷特性不仅与能源价格有关，还与能源供应方式相关，因此，P2G等能量转换设备的参与对缓解供电系统在用电高峰期的供电压力，以及系统调度结果也有重要影响。下面通过下述两种工况进行分析。

(1)工况1：不考虑多元化价格需求响应和P2G、电锅炉和电制冷等能量转换设备对系统的影响。

此工况下，IES系统由风力发电机组、光伏发电机组、储能设备、CCHP机组以及外部能源共同作用。CCHP系统通过燃料带动燃气轮机、发电机等燃气发电设备运行，产生的电力供应用户的电力需求，系统发电后排出的余热还能通过余热回收利用设备向用户供热、供冷。优先考虑由风力发电机组和光伏发电机组联合供应电负荷需求，再由CCHP机组中的燃气轮机补足不足，若仍无法满足系统电负荷需求，需要购买外部能源。另外，由于燃气轮机在发电过程中产生的余热经余热锅炉吸收后，可由制冷机或换热装置转换成冷、热能，因此，考虑用该冷、热能满足系统冷、热负荷需求，再由外部能源提供剩余不足。

(2)工况2：考虑多元化价格需求响应和P2G、电锅炉和电制冷等能量转换设备对系统的影响。

若风力发电机组和光伏发电机组满足系统电力负荷需求后仍有剩余，剩余能量可进行储电或经由P2G等转换设备进行电转气、电转冷、电转热，以满足系统中除电能外的其他供能要求。同时，优先利用电锅炉、电制冷等能量转换设备，对系统中的冷、热负荷需求进行供应，再由外部设备提供剩余不足。

图8为不同工况下的供电需求。工况1下，在用电高峰期，风力发电机组和光伏发电机组无法单独满足用电负荷需求，在17 h，两者供电最高87.65 MW，同时需要储能设备、燃气轮机和外部能源共同配合给用户供电；在8 h ～12 h和15 h ～19 h，储能供电约6 MW；在7 h～12 h时和15 h～22 h，燃气轮机供电约26 MW；外部能源供电最高达44.6 MW。工况2下，外部能源供电较少，主要是由于多元化需求影响的实施，使用能结构发生变化。

图8 不同工况下的供电情况Fig.8 Power supply under different working conditions

图9和图10分别为不同工况下的供冷、供热情况，由分析可知，在工况1下，CCHP系统无法满足冷、热负荷的需求，分别经制冷机于15时最高满足了约29.1 MW的冷负荷，经换热装置于21时最高满足了约19.53 MW的热负荷。系统主要依靠外部供能进行冷、热负荷补给；在工况2下，电制冷、电锅炉与CCHP共同参与系统冷、热负荷需求。在23时～6时，电制冷满足了均高于10 MW的冷负荷需求；15时，制冷机满足了最大29.2 MW的冷负荷要求。在0时～5时，电锅炉满足了约21.2 MW的热负荷需求；在22 h，换热装置满足了最大约22.9 MW的热负荷需求，最多仅9.69 MW的电负荷需求由系统外部装置提供。

图9 不同工况下的供冷情况Fig.9 Cooling under different working conditions

图10 不同工况下的供热情况Fig.10 Thermal under different working conditions

实施需求响应前、后调度对比如表4所示。相比于工况1，工况2下系统的净收益增加约20万元，用户总用能支出降低了约17.8万元。其中，用户电、热和冷用能的支出分别降低了16.5万元、1.1万元和0.19万元，CO2等有害气体排放量降低。结合图9、图10，以及表4进行分析可知，在工况2下，多元化的价格需求响应可有效地转移用电、用热等负荷，而电制冷、电锅炉、P2G等能量转化设备能够在用电低谷实施弃能消纳，大幅提高能源的利用率。

表4 实施综合需求响应前、后效益对比Tab.4 Comparison of benefits before and after IDR

5.2 HP-NSGA-Ⅱ算法求解

采用TOPSISN方法分别寻找文中NSGA-Ⅱ和HP-NSGA-Ⅱ两种算法下 Pareto 前沿解中的最理想解，由表5不同算法下各主体收益情况可知，相较于NSGA-Ⅱ，HP-NSGA-Ⅱ 所得调度方案下的各主体经济性均更佳。

表5 不同算法下各主体收益Tab.5 Revenues of agents under different algorithms

6 结束语

本文在IDR研究的基础上，综合考虑了能源价格对电力、天然气、热能等能源消耗量的影响，构建了多元化用能价格需求响应模型；以经济和环境成本最小为目标，建立了基于DR机制的IES多目标动态运行优化模型，并采用基于超平面投影的NSGA-Ⅱ(HP-NSGA-Ⅱ)算法进行求解，通过算例分析验证，得到如下主要结论：

(1)考虑NSGA-Ⅱ在处理多目标动态优化调度中的主要缺陷，引入超平面投影 HP(Hyperplane Projection)的方法，对NSGA-Ⅱ算法进行改进，有效地提高了算法的收敛性;

(2)IES多元价格需求响应的实施，可以有效改变用户的用能习惯，在增大了系统净收益的同时，减小了用户用能的总成本，提高了系统运行经济性，研究成果具有实际工程意义。