基于高斯核密度估计的典型负荷曲线形态聚类算法

严明辉， 谢雄， 李维劼， 吴滇宁， 崔雪， 潘舒宸

(1.昆明电力交易中心有限责任公司，昆明 523000; 2.武汉大学 电气与自动化学院， 武汉 430072)

0 引 言

2019年国家发改委、能源局发布《关于深化电力现货市场建设试点工作的意见》以来，首批8个电力现货试点纷纷启动结算试运行，现货市场建设推进速度明显加快[1]。在现货市场结算中，实时要实时反映电力供需关系变化，因而有时实时电价波动会很剧烈，同时由于现货市场采用价-量结算，故实时电量的准确性决定了现货市场结算的准确性。由于各种计量装置或传输问题，很多用户的电量并不能实时获得，这种用户称为非分时计量用户，此时需要通过电力曲线将该类用户的日电量分解至每日以15 min为间隔的分时电量，该电力曲线可称之为典型负荷曲线。目前广东电力市场非分时计量用户的日电量分解计划是对所有的用户通过每日的峰平谷三个时段进行电量的比例分配[2]。这样对一个用电规律明显的大用户来说，一个时段内的曲线时段上微小的波动引起的电费差距可能很大。相对日电量按固定比例分配，建立一个动态的每日96个点的典型负荷曲线模型能有效提高日电量分解准确率。由于每个区域电力市场包含了海量用户的负荷数据，不能给每个市场化用户建立其典型负荷曲线模型，如何通过有效的负荷曲线形态分类方法来把握不同用户的用电特性，具有相同用电曲线的用户选用相同的典型负荷曲线进行现货市场日电量的分解；同时如何提高典型负荷曲线的日分时电量曲线的准确性成为了关乎现货市场进一步深入推进的关键。

为了解决上述问题，本文选用负荷曲线形态聚类后的聚类中心作为簇内的典型负荷曲线用于簇内所有用户的日分时电量分解。从而可以通过提高聚类中心描述同类簇下所有曲线的能力来提高所有用户日分时电量分解时的准确性。目前国内外关于负荷曲线形态分类问题的研究较为完备，主要通过无监督学习的聚类方法获得。包括快速密度峰值算法[3]、基于斜率提取边缘[4]、模糊c均值聚类和谱聚类[5-7]等聚类算法和利用降维方法来提高聚类效果如强化学习机[8]、自编码器降维[9]、奇异值分解降维[10]、自组织映射降维[11]等。传统聚类算法为了提升分类效率，一定程度上牺牲了聚类中心描述同类簇负荷曲线的能力和准确性。如Kmeans算法是一种基于距离的无监督学习分类方法，其聚类中心是通过同类簇的均值法获得，通过不断迭代计算同类簇下曲线与聚类中心的欧式距离，来获得分类结果[12]。聚类中心只是为了获取分类结果的一个过程比较参数，聚类中心的描述能力仍可进一步提高。同时在传统聚类算法中，核密度估计(Kernel Density Estimation，KDE)只用于选取Kmeans聚类的初始聚类中心，从而来提升分类效果[13]。但是只能保证初始聚类中心在第一次迭代计算中，描述能力是最好的。而在后续的迭代计算中，不能保证典型负荷曲线的簇内描述能力。

基于此，为了提升聚类中心描述同类簇的能力，本文将核密度估计的思想引入Kmeans聚类算法中的聚类中心每一次形成过程，将原有的均值获取聚类中心升级为高斯核密度估计获取最大概率的聚类中心进行迭代计算。典型负荷曲线获取流程如图1所示，利用电力负荷数据进行数据准备和改进Kmeans算法聚类，最后以云南省电力计量数据为例，对提出的算法与传统聚类算法、传统日电量分解方法进行了比较。结果显示基于核密度估计改进聚类中心的Kmeans-KDE算法获得的典型负荷曲线在用于现货市场日电量分解时准确性更高。

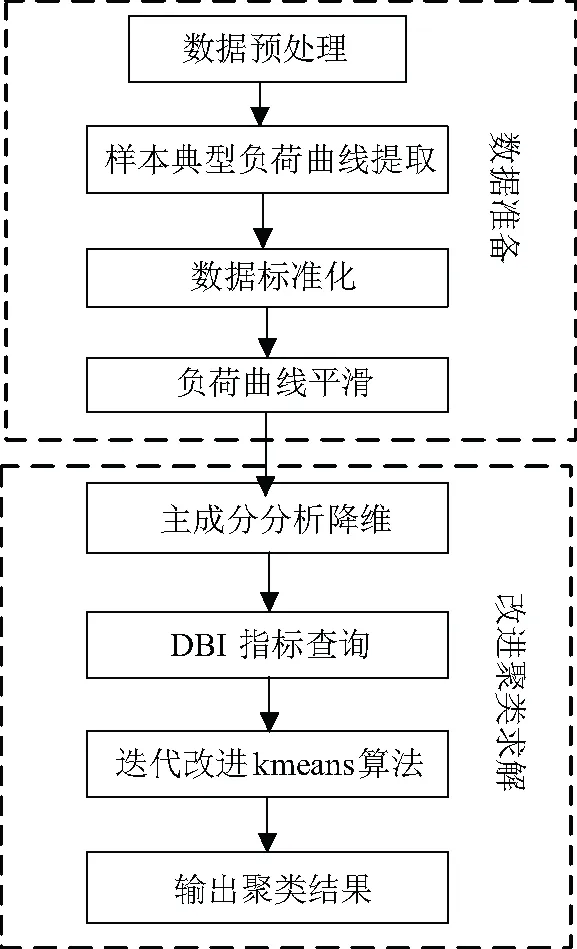
图1 典型负荷曲线形成框架Fig.1 Typical load curves frame

1 负荷数据准备

为了解决非分时计量用户的电量分解问题，选择具有相似用电规律的分时计量用户的典型负荷曲线提供其进行结算。如不具备分时计量的超市参与现货市场时，需要根据具有分时计量超市的典型负荷曲线进行日电量的分解。故需要选择具有分时计量能力的样本用户，为了样本用户能充分模拟真实的全省负荷，样本用户的选取涵盖了各个行业，各个电量等级。由于电力计量状况不一，存在漏数、串数等异常情况，需要对各样本数据进行预处理。

1.1 数据预处理

1.1.1 异常数据处理

对于异常数据，根据计量值累加递增原则即下一个时刻的计量值大于等于此刻的计量值小，记录异常值位置，对该位置的数据做缺失值处理。

1.1.2 缺数处理

对于用户负荷电量缺数较少的情况，采用三次样条插值法[14]进行插补。对于缺值较多的用户，采用垂直修复法进行修复。即选用前一周同一时刻对应的负荷值作为此刻的负荷值。对于缺值太多的用户不宜选为样本用户。

1.2 典型负荷曲线提取

1.2.1 提取样本日负荷曲线

经过数据预处理后，得到了样本用户全年一共35 040个时间序列点计量数据。为了得到特定场景下(特定月份)的样本典型负荷曲线，需要进一步对该样本用户的不同场景(工作日、休息日、节假日)进行日负荷曲线提取。采用基于高斯核函数概率密度分布的方法进行负荷曲线提取。以6月份的工作日场景为例。该场景下任一个时序点的电量等于该月22个工作日的电量数据进行概率密度的叠加。

其中Gaussian核函数K，其计算公式为：

(1)

计算该用户历史负荷数据第k时刻负荷值xk_num对应的概率密度函数fk(xk_num)，其表达式为

(2)

式中K为高斯核函数；T为时序k下的样本点数目；h为带宽；xk_num∈[xk_min,xk_max]；xik为第i日k时刻的负荷值；xk_min为该用户历史负荷数据第k时刻的负荷最小值；xk_max为该用户历史负荷数据第k时刻的负荷最大值。

根据式(2)，形成最大概率密度曲线向量，Xi_mp=[xi_mp_1,xi_mp_2,…xi_mp_k,…,xi_mp_96]T，这条最大概率密度曲线作为该样本用户的典型负荷曲线，其中xi_mp_k为fk(xk_num)取最大值时xk_num对应的数值。

1.2.2 数据标准化

样本用户使用电量的数量级具有较大差异，而典型日负荷曲线提取是为了把握该样本用户的负荷规律，即目的在于曲线的形状而非曲线的电量值。故可以通过数据标准化，对数据按比例缩放，使之落入一个特定区间进行曲线形状的描述。文中设置所有样本用户一天内的96个时序用电量之和为1 000 kWh，便于不同量级的用户能够进行比较和加权，如式所示。

(3)

1.2.3 负荷曲线平滑

用户用电数据存在用户数据由于其一定的用电随机性，负荷曲线容易出现一定的上下波动的情况，而进行负荷曲线预测时，希望把握负荷的曲线变化规律，因此部分曲线出现的噪音点将会干扰负荷波动形态的判断。鉴于上述问题，最后使用高斯滤波(Gauss Filter, GS)进行用户典型曲线的平滑[15]。

原有的用户计量数据为不完整的电量数据，经过前文所述的数据预处理后，可得到任意月份的典型日负荷曲线。经过平滑后的某超市2018年6月的工作日典型负荷曲线如图2所示。

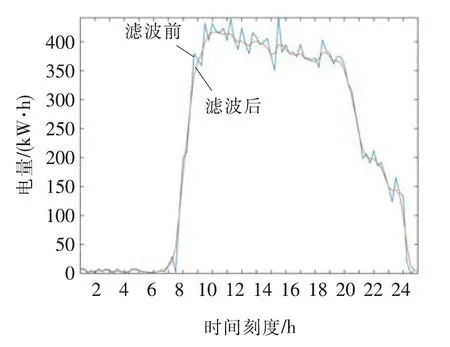
图2 某超市2018年6月工作日典型负荷曲线Fig.2 Typical load curve of working days in June 2018 of supermarktet

2 基于核函数估计的Kmeans聚类

2.1 主成分分析法降维

数据降维可提升后续聚类算法的效率，同时能够舍弃掉噪声影响的数据。文献[16]中指出对于负荷曲线降维，主成分分析降维可取得最佳效果；因而选用主成分分析法进行用户数据降维。

主成分分析基于最大可分性，将样本用户在超平面上实现可分。PCA算法流程如表1所述。其中，降维后维数d根据特征向量的描述能力决定。

表1 主成分分析算法流程Tab.1 Principal component analysis algorithm flow

2.2 改进kmeans聚类算法

2.2.1 聚类有效性评价

数据集中含有N条样本负荷曲线，每条负荷曲线可以表示为96维的向量。由于聚类的样本负荷曲线没有标签，为无监督学习。故为了衡量聚类的效果，引入聚类有效性指标有误差平方和(Sum of Squared Error，SSE)、Davies-Bouldi 指标(Davies-Bouldin Index，DBI)等[17]。根据聚类有效性指标确定最佳聚类数目，实现kmeans聚类数目的准确输入。

(1)SSE指标

误差平方和SSE用于衡量簇内各子类至聚类中心的欧氏距离，即：

(4)

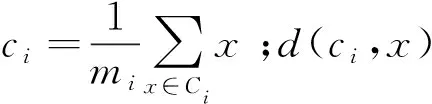
(2)DBI指标

DBI指标能有效描述簇内的相似性和簇之间的相差性。

(5)

式中:

(6)

式中d(Xk)和d(Xj)为簇内样本内部距离；d(ck,cj)为聚类中心的距离；IDBI越小表示聚类效果越好。

2.2.2 基于核密度估计的Kmeans聚类算法

传统Kmeans聚类算法是根据欧式距离来对样本的相似性进行的分类的方法。算法流程如表2所示。在传统Kmeans算法中第10步计算新的均值向量时，采用等权重平均值叠加形成的新的聚类中心。然而在实际中，均值法聚类中心提高了算法效率，但是对聚类中心的聚类质量也有一定下降。为了提高对典型负荷曲线描述用户用电特点的准确性。基于概率统计的思想，提出一种新的聚类中心形成方法，如图3所示。采用高斯核函数概率密度分布函数拟合样本最大概率分布函数，然后根据簇内的其他曲线与最大概率曲线的概率分布进行加权叠加，获得新的聚类中心形成数据的划分。结果显示新聚类中心能更精准描述簇内用户的负荷曲线。

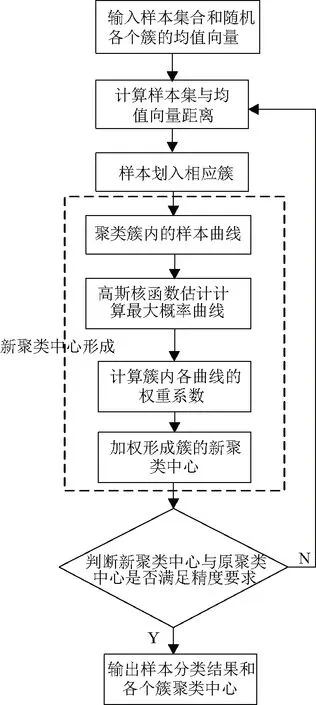
图3 改进Kmeans聚类算法流程Fig.3 Process of clustering center algorithm for kernel density estimation

表2 Kmeans算法流程Tab.2 Kmeans algorithm flow

新的聚类中心形成过程包括

(1)根据式(2)计算时序k的负荷值xk_num对应的概率密度函数fk(xk_num)，其中K为高斯核函数，T为时序k下的样本点数目，h为带宽；xik为簇内的第i条曲线时序k的负荷值；xk_min为簇内历史负荷数据第k时刻的负荷最小值；xk_max为簇内历史负荷数据第k时刻的负荷最大值。

(2)迭代计算各个时刻(1～96)的概率密度函数，形成最大概率负荷曲线Xi_mp=[xi_mp_1,xi_mp_2,…,xi_mp_96]T，其中xmp_k为fk(xk_num)取最大值时xk_num对应的数值。

(3)计算簇Cλj内第i条负荷曲线Xi=[xi1,xi2,…,x96]T相较于最大概率负荷曲线Xi_mp=[xi_mp_1,xi_mp_2,…,xi_mp_96]T的权重wi。

(7)

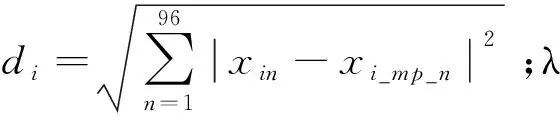
(4)对簇内所有的负荷曲线进行加权叠加，以获得新的聚类中心。

(8)

3 算例分析

文中选用从2018年7月1日至2019年7月1日的云南全省16市1 250,家用户涵盖钢铁、冶炼、金属等大工业用户以及超市、酒店等一般工商业用户以15 min为粒度的负荷计量数据。经过前述提及的数据预处理、提取的典型负荷曲线、数据标准化、曲线平滑后得到的负荷曲线数据进行基于核函数估计的Kmeans聚类分析。

3.1 聚类质量评价

首先，对负荷曲线经进行聚类有效性检测，结果如图4所示，在不同聚类数目时，DBI指标呈现出波动性，当聚类数为8时，DBI指标取至极小值。此时意味着聚类效果最好。因而选择聚类数8进行下一步的聚类。

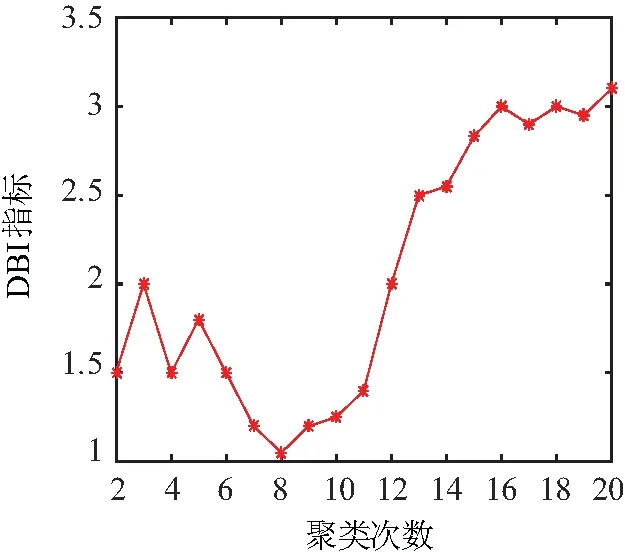
图4 DBI指标确定最佳聚类数目Fig.4 Davies-Bouldi Indexes determine the optimal number of clusters

3.2 负荷数据集聚类结果分析

对样本库典型负荷曲线进行主成分分析后，原有的数据进行了降维。如图5所示，原有的一天96维度的负荷数据经主成分分析后，在保持95%的贡献率下，降维成了13维。此时描述负荷曲线能力没有下降，低维的数据描述了原有的高维曲线特性。

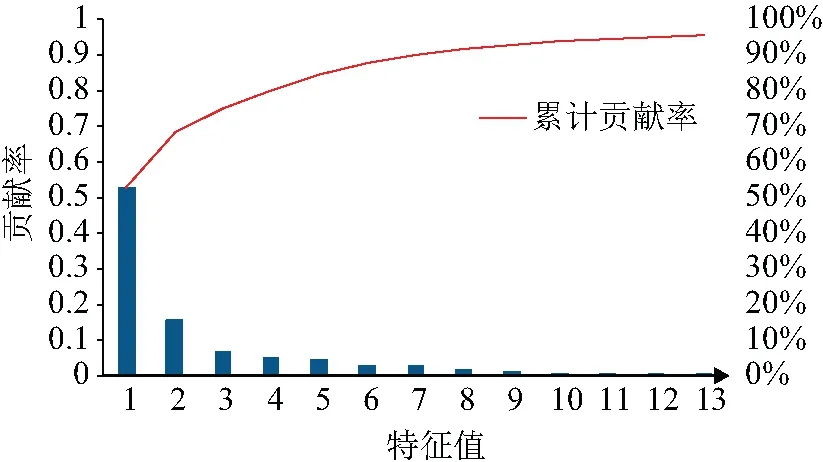
图5 主成分分析结果Fig.5 Principal component analysis results

由于负荷曲线以15 min为分解粒度，故每日共计有96个时序点。每个点对应的值为该15 min内的用电量。利用降维后的负荷数据作为聚类算法的数据矩阵，运用基于核密度估计的Kmeans算法进行聚类。结果如图6所示。

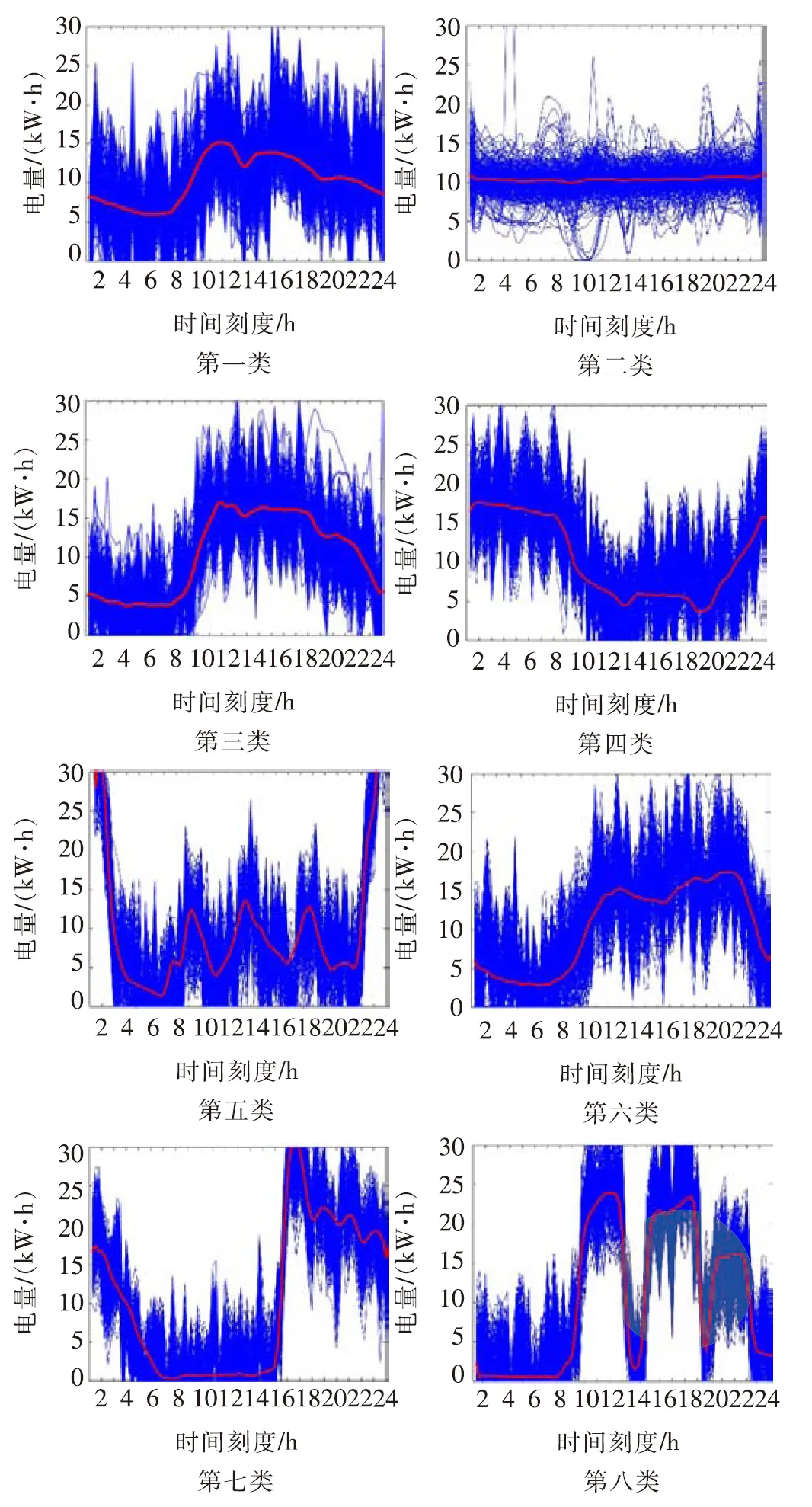
图6 聚类结果示意图Fig.6 Schematic diagram of clustering results

结果显示负荷曲线形态分类效果较好。用电曲线大致分为单峰(第三类)、双峰(第一类、第六类)、三峰(第八类)、避峰(第七类、第五类、第四类)、平峰(第二类)等。大多数大工业用户为追求效率最大化选用全天24小时连续运行，因而呈现出单峰。部分工业用户对电价敏感采用峰谷运行方式，白天少用电，晚上多用电，呈现出避峰的典型负荷曲线形态。对于超市、商业综合体等营业时间考虑人流量和白天的活动时间，从早上至晚上营业。因而呈现出单峰或者双峰的形态。云南采矿业发达，对于小型的页岩砖厂以及小工业用电，其用电特性与工作人员的休息时间息息相关，呈现出三峰的用电曲线形态。聚类结果与实际全省不同用户的不同用电规律相契合。

3.3 曲线描述能力比较

改进kmeans-KDE算法曲线描述能力有了进一步提高，典型负荷曲线能更好的用于日电量的分解。为进一步对新算法下的典型负荷曲线的描述能力有一个更直观的比较，通过不同聚类中心形成方法、不同算法、不同典型负荷曲线分解实例来对改进kmeans-KDE算法的典型负荷曲线描述能力做定量的比较。

选用均值法、正态核(正态分布)[12]、高斯核下产生聚类中心迭代对最终聚类结果的影响进行比较。结果如图7所示，对比可知三种方法产生的聚类中心的形状曲线大致走势相同，但是正态核描摹的聚类中心出现了多处局部突变为零。引入SSE指标量化对比三类方法的误差平方和，结果如表3所示，高斯核密度估计的聚类中心相较传统的均值法聚类中心，误差平方和SSE更小，相较能更好的描述簇内各曲线的相似性。聚类中心作为典型负荷曲线描述能力更强，典型负荷曲线用于现货市场电量分解时，准确性更高。

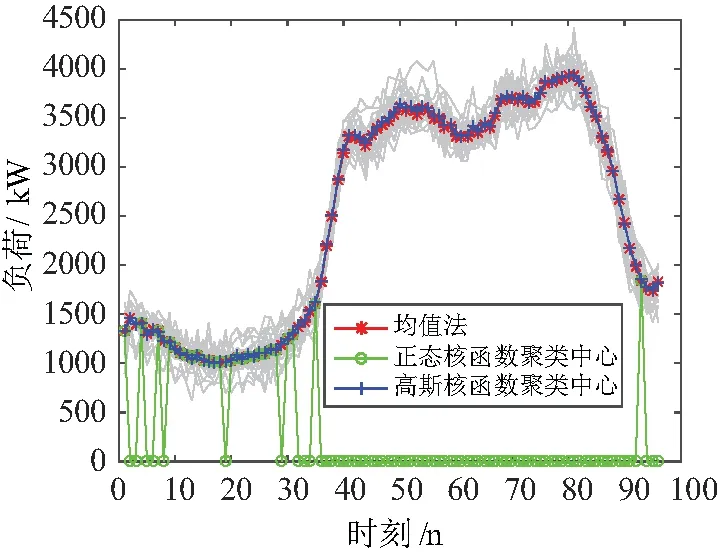
图7 高斯核估计与其他方法聚类中心比较Fig.7 Comparison of Gaussian kernel estimation and other method cluster center

表3 三类方法SSE指标比较Tab.3 SSE index comparison of three methods

选取传统算法聚类和新算法在同一个数据集进行聚类，结果比较如表4所示。经过降维后的基于核密度估计的Kmeans算法相较其他聚类算法虽然在耗时上有所增加，但是在SSE指标聚类中心的误差平方和最小，意味着在同一个簇的各曲线的相似度更高。DBI指标较小，在簇内相似性和簇间相异性均能有较为优异的效果。意味着核密度估计改进聚类中心的新算法相较传统聚类算法不仅提高了典型负荷曲线的描述能力，同时提高了负荷曲线形态分类的效果。

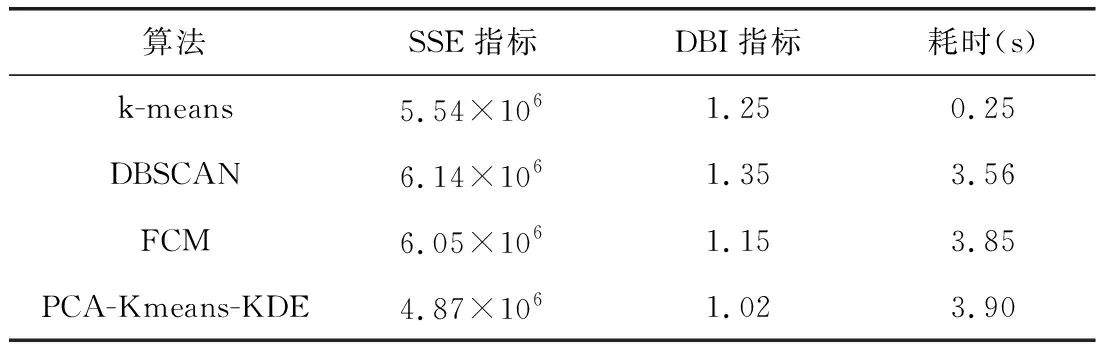
表4 算法结果比较Fig.4 Comparison of algorithm results

算法结果中的各项指标印证了典型负荷曲线相较传统算法描述能力有了提高。为了比较在具体实例中传统算法曲线分解、峰谷平分解、改进Kmeans-KDE算法曲线分解日电量的准确性，以云南省某铝冶炼厂某一日真实计量值为例，负荷采集间隔为15 min。如图8所示。

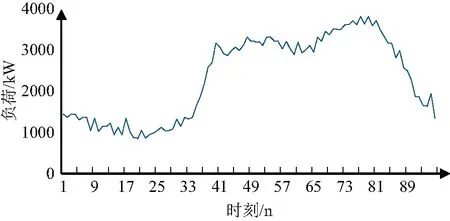
图8 某用户某日真实负荷曲线Fig.8 The real load curve of a user on one day

该用户日电量总计为223 732.5 kW·h。当用户该日所有电量缺失时，需要恢复该日96点真实电量用户现货结算，由于前文采用了数据标准化，故电量恢复公式如下所示:

用户该日真实负荷曲线=该日电量/1 000×96点典型负荷曲线值

当该日分时计量值缺失时(模拟非分时计量用户)，选用三种不同方法进行真实负荷描述能力的比较。

(1)峰谷平曲线D1分解

根据广东电力市场峰谷平曲线D1[2]进行日电量均分分解，即将日电量平均分解至每日峰段、平段和谷段。分解结果如图9所示。

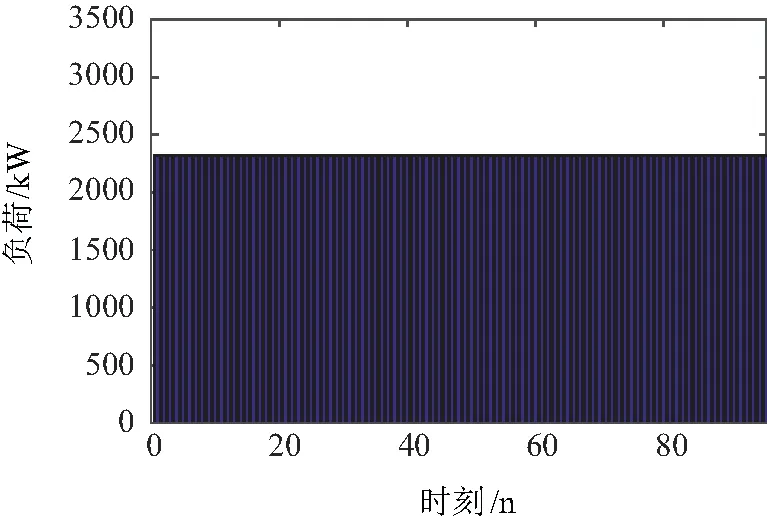
图9 峰谷平D1曲线-电量分解结果Fig.9 Peak valley level D1 curve-result of electric quantity decomposition

(2)传统算法负荷曲线分解

以传统算法中Kmeans算法为例[12]，获得该样本用户的分类结果，利用其典型负荷曲线对日累计电量进行分解，日电量分解结果如图10所示。

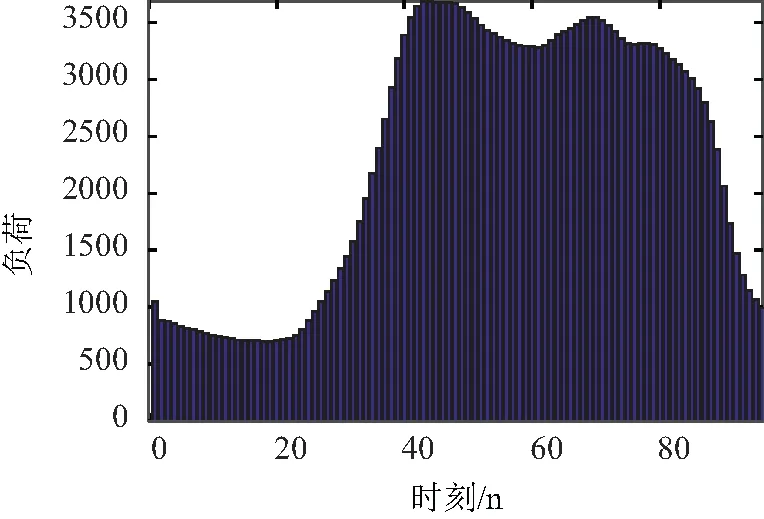
图10 传统聚类算法-电量分解结果Fig.10 Traditional clustering algorithm-power decomposition results

3)改进Kmeans-KDE算法典型负荷曲线分解

利用改进Kmeans-KDE算法提取的典型负荷曲线对日累计电量进行分解，日电量分解结果如图11所示。

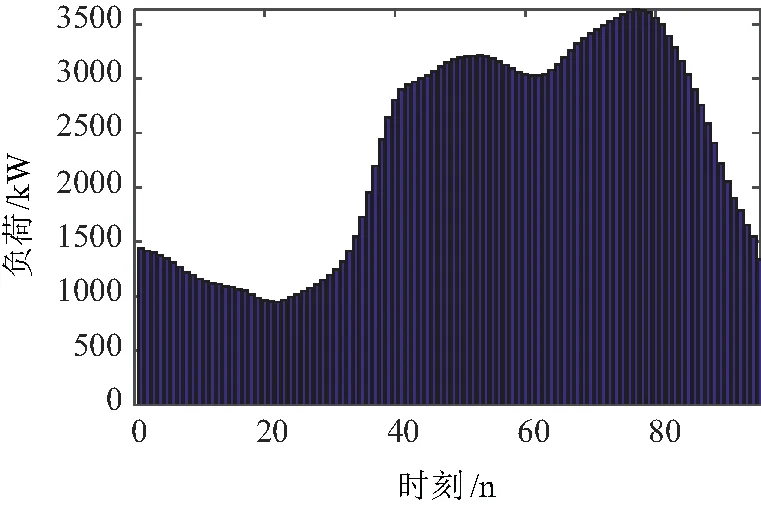
图11 改进Kmeans-KDE算法-电量分解结果Fig.11 Improved Kmeans-KDE algorithm-power decomposition results

以分解后的电量曲线与真实负荷曲线的96个点误差率平均值作比较，其中误差率计算方法如式(9)所示，计算结果如表5所示。

表5 不同曲线分解方法误差率Tab.5 Error rate of different curve decomposition methods

误差率=|真实值-分解值|/真实值

(9)

改进Kmeans-KDE算法获得的典型负荷曲线用于用户日电量分解时，相较其他方法得到的日分时分解曲线，误差率更低，典型负荷曲线描述真实负荷波动时，描述能力更强。

4 结束语

为了解决现货市场背景下，市场化用户日电量分解的准确性问题,文中提出了基于核密度估计改进Kmeans算法的典型负荷曲线形态聚类方法，利用高斯核密度估计获得聚类中心代替原有的均值法获得聚类中心，并将其作为典型负荷曲线参与现货市场日分时电量分解。最后，运用云南省样本用户计量数据进行算例分析，结果显示，文中所提算法不仅负荷曲线形态分类效果较好，同时获取的典型负荷曲线参与现货市场的日电量分解时准确性更高，可为现货市场结算试运行提供了相应的技术撑。