优化负载变换器输入阻抗的输入电流内环控制方法

王 剑 贾鹏宇 李 艳 郑琼林 郭希铮

（北京交通大学电气工程学院 北京 100044）



优化负载变换器输入阻抗的输入电流内环控制方法

王 剑 贾鹏宇 李 艳 郑琼林 郭希铮

（北京交通大学电气工程学院 北京 100044）

摘要为提高级联系统的稳定性，应尽量减小源变换器输出和负载变换器输入阻抗的交集区。一方面，尽量减小源变换器的输出阻抗；另一方面，尽量增大负载变换器的输入阻抗。基于DC-DC变换器的一般性小信号模型，提出以平均输入电流环为内环、输出电压环为外环的双环控制方法，分析在这种控制方式下影响变换器输入阻抗的因素，并给出改变内环电流采样系数前后变换器输入阻抗的量化计算过程。分析表明，当电流内环的截止频率大于电压外环截止频率时，增大电流采样系数，能够提高电流内环环路增益，有效增大负载变换器的输入阻抗。从而在级联系统中，能够有效减小负载变换器的输入阻抗与源变换器输出阻抗的交集，提高级联系统的稳定性。通过仿真和实验验证了所提方法的有效性。

关键词：级联系统 DC-DC变换器 输入阻抗 输入电流 稳定性

北京市科技计划课题资助项目（Z141100003114011）。

0 引言

在级联系统中，源变换器的输出阻抗Zout和负载变换器的输入阻抗Zin是影响级联系统稳定性的重要参数。为提高级联系统的稳定性，应尽量减小源变换器输出和负载变换器输入阻抗的交集区。一方面，减小源变换器的输出阻抗；另一方面，增大负载变换器的输入阻抗。

针对输入阻抗的优化，文献[1]提出了适用于无刷直流电机系统的补偿负阻特性控制方法，以改善变换器的输入阻抗，增加LC滤波器的阻尼，避免系统发生振荡。对变换器应用于功率因数校正（Power Factor Correction,PFC）电路的情况，文献[2,3]根据PFC电路中输出电容较大的特点，简化了变换器模型，分别针对Boost、Cuk和Sepic变换器进行了电流内环控制下的稳定性分析，优化了上述变换器的输入阻抗，减弱了变换器和EMI滤波器之间的相互作用。

本文以改善变换器的输入阻抗为目的，基于DC-DC变换器的通用小信号模型，提出输出电压外环、输入电流内环（Input Current Inner Loop，ICIL）的双环控制方法，并分析在这种双环控制方式下，影响变换器输入阻抗的因素，提出优化的方法，为变换器输入阻抗的设计提供依据。

传统的双环控制方法大多以提高输出响应的快速性为目的，其电流内环的采样点位置不固定，一般根据不同变换器拓扑而改变，且大多采用峰值电流控制，以拓扑中的电感电流为被控量，实现模型的降阶。ICIL双环控制方法以平均电流环为基础，固定采样变换器的输入电流，以DC-DC变换器的小信号模型为出发点进行分析，因此结论具有一般性。

1 采用ICIL控制的DC-DC变换器小信号模型

在级联系统中，源变换器的输出阻抗和负载变换器的输入阻抗相互影响，决定级联系统的稳定性。图1给出了一般性闭环控制的变换器对应的输入阻抗和输出阻抗示意图。

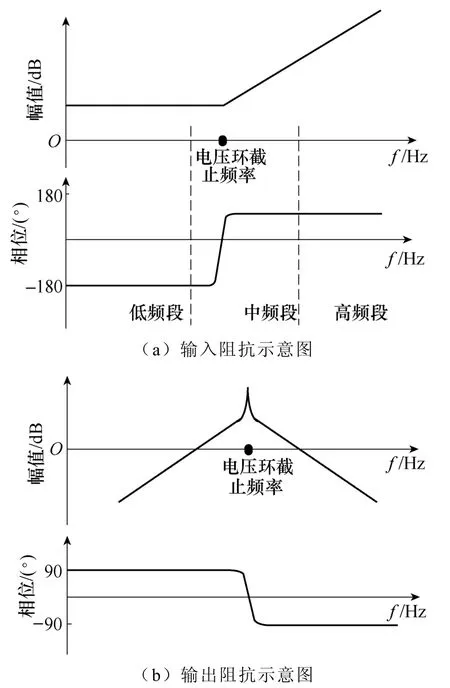
图1　级联系统负载变换器输入阻抗和源变换器输出阻抗典型伯德图Fig.1 Typical Bode plots of input impedance in load converter and output impedance in source converter of a cascaded system

级联系统中的负载变换器大多以控制输出电压为目标，因而负载变换器一般以电压闭环进行控制。所以，负载变换器常处于功率恒定的状态，这里设其功率为PL，并且设输入电压、电流的稳态平均值分别为Vg和Ig。显然，在稳态工况时可得到

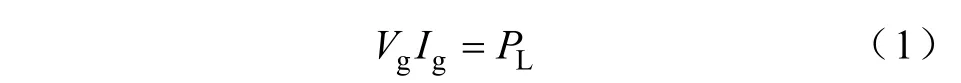
在频率远小于电压环截止频率的低频段，由于电压闭环的作用，变换器的输入功率恒定。当输入电压缓慢变化且其增量为Δvg时，其输入电流必然发生相应变化，假设其增量为Δig，因此有

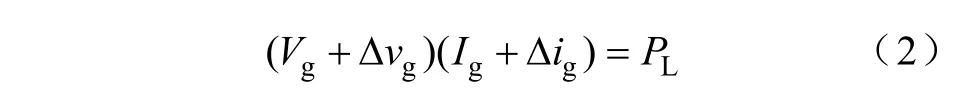
将等式（2）展开，可得

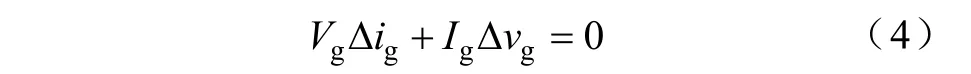
根据输入阻抗的定义，可知在闭环负反馈的作用下，变换器的低频段输入阻抗为

可知，低频段的输入阻抗表现为负阻特性，相频曲线的渐近线等于-180°，如图1a所示。

在大于电压环截止频率的高频段，由于闭环负反馈的作用逐渐减弱，因此其闭环输入阻抗基本等于开环输入阻抗[5,6]。在高频处，由于变换器输入滤波器的影响，其输入阻抗主要受输入滤波电感的影响，所以其幅频曲线呈现20dB/dec的斜率上升，相频曲线的渐近线趋于90°，如图1a所示。

由文献[6-8]可知，变换器的闭环输出阻抗与输出滤波器参数和闭环截止频率相关，呈现出电阻、电感以及电容三者并联的特性，且其谐振峰值的频率取决于电压环截止频率。变换器闭环输出阻抗的示意图如图1b所示。

若输出阻抗和输入阻抗在全频率范围内均无交集，则系统必然稳定，这就是Middlebrook稳定判据。在远低于电压环截止频率的低频段频率范围内，变换器的输入阻抗表现为负阻特性，其相频曲线等于-180°。如果输入、输出阻抗在这一频段内相交，则阻抗比对应的奈奎斯特曲线必定包围（-1，j0）点，不满足稳定判据，此时级联系统必然不稳定[5,7]；在电压环截止频率附近的中频段频率范围内，由于电压环的反馈作用逐渐减弱，因此输入阻抗逐渐偏离负阻特性，如果与输出阻抗在此频段范围内相交，需要判定阻抗比是否满足奈奎斯特稳定判据，从而判断级联系统的稳定性；在远大于电压环截止频率的高频段频率范围内，由于反馈控制环路基本不影响这一频段，变换器的闭环输入阻抗基本等于开环输入阻抗，如果阻抗交截发生在这一频率范围内，也不会产生不稳定现象。

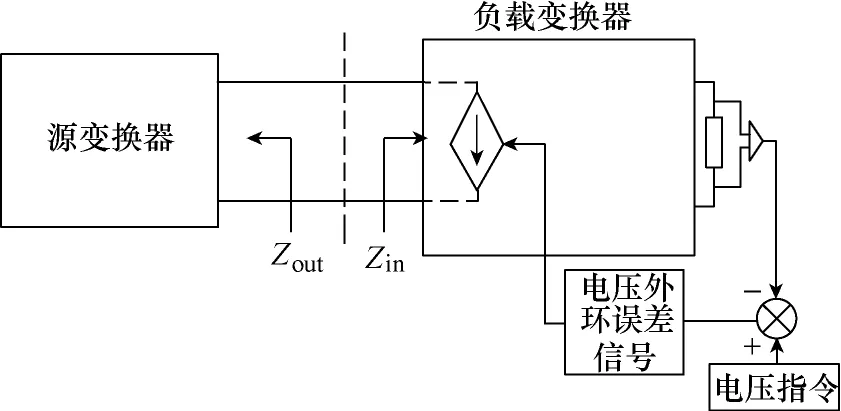
图2　级联系统中负载变换器引入ICIL双环控制方法示意图Fig.2 Sketch map of the ICIL control method in a load converter of the cascaded system

理想电流源的输入阻抗为无穷大，因此其小信号模型等效为开路。如果级联系统中负载变换器的输入电流取代输出电压作为被控量，其输入阻抗将不会呈现负阻特性，而表现为电流特性，此时其输入阻抗得到大幅度提高，级联系统的稳定性将得到改善。然而如果仅控制输入电流，负载变换器的输出电压将会失控，无法完成对后级负载电压的调节作用。因此，如果变换器采用外环恒定输出电压、同时引入ICIL的双环控制策略，将既保证变换器的输出电压可控，又可使变换器的输入阻抗在一定频率范围内表现为电流特性，如图2所示。采用ICIL双环控制时，由于负载变换器存在输出电压外环，因此在远小于电压环截止频率的低频段，变换器依然呈现负阻特性，这是由其功率恒定的特性决定的，如图3所示。在采用双环控制时，电流内环截止频率一般远大于电压外环，因此在电压环截止频率至电流内环截止频率范围的中频段，负载变换器的输入阻抗将表现为电流负载特性，此时变换器的输入阻抗将增大；在频率大于电流环截止频率的高频段，内外环的反馈作用基本不产生影响，因此变换器的输入阻抗表现为开环输入阻抗特性。由上述分析可知，在大于电压外环截止频率而小于内环截止频率范围内，变换器的输入阻抗将得到提高。

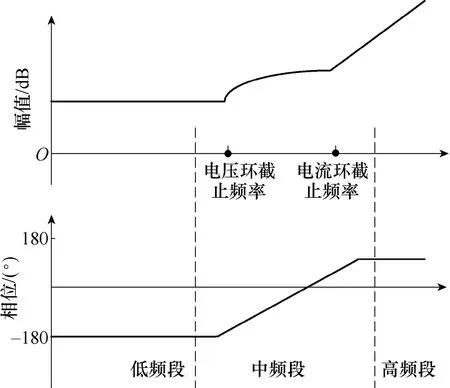
图3　引入ICIL双环控制的输入阻抗伯德图Fig.3 Bode plots of input impedance with ICIL double-loop control

1.1 引入ICIL双环控制的输入阻抗分析

根据DC-DC变换器小信号模型可知，变换器在输入ICIL控制方式下，其闭环小信号模型如图4所示。

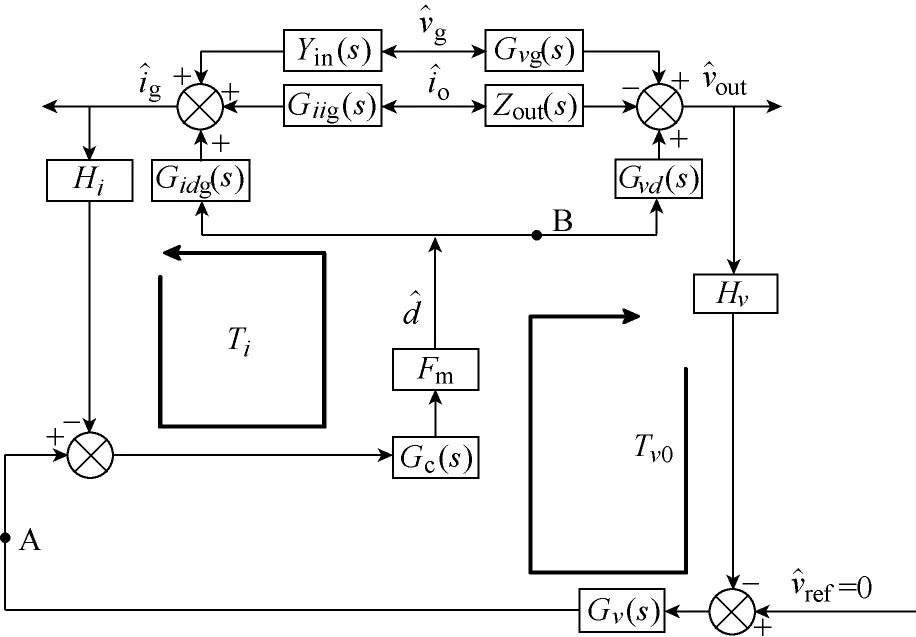
图4　ICIL控制的变换器小信号模型框图Fig.4 Block diagram of the small signal model with ICIL control

在此控制方式下，变换器的输入阻抗Zin_c可表示为

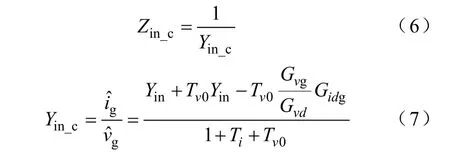
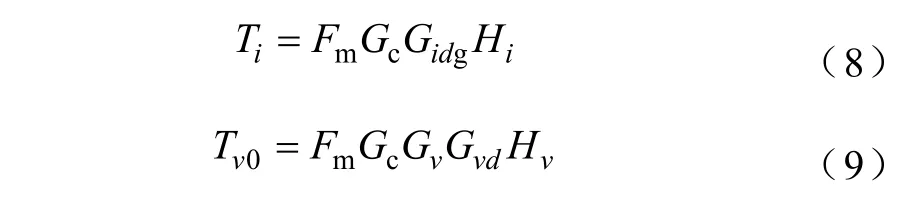
式中，Yin_c表示双环控制对应的闭环输入导纳；Ti表示电流内环的环路增益；Hi和Hv分别表示输入电流、输出电压采样系数；Gc表示电流内环控制器；Gv表示电压外环控制器；Tv0表示当电流采样系数Hi等于零时变换器的外环环路增益。

同样，可通过式（6）～式（9）求得变换器的电流内环闭环传递函数Gicl，即图4中从A点至B点的传递函数为

由式（10）可求得变换器在ICIL双环控制时的电压外环环路增益Tv为

由图4可知，当变换器的输入电流采样系数Hi＝0时，变换器相当于处于单电压环工作模式，定义此时的变换器输入阻抗为Zin_c0，输入导纳为Yin_c0，则有

可知，此时的电压环的环路增益即为式（9）中的Tv0。

根据式（12）和式（13），可将式（7）表示为

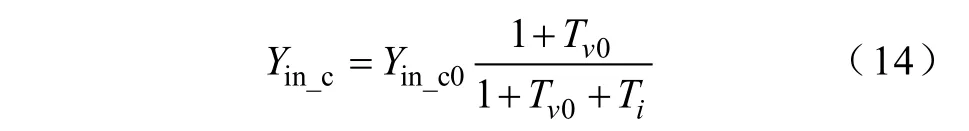
由于在分析变换器的传递函数时，多用频域下的对数坐标系，因此对式（14）两边取对数，可得

由式（15）可得

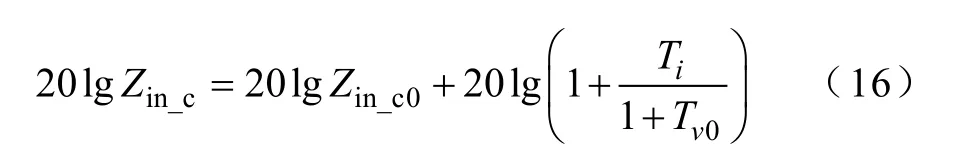
由图4可知，在变换器设计中，一般被控对象传递函数是固定的，因此需要对控制器Gv、Gc以及采样系数Hv、Hi进行分别设计，以实现变换器特性的优化。由式（16）可知，在ICIL控制模式下，输入阻抗与三个变量相关，即电流采样系数Hi＝0时对应的单电压环闭环输入阻抗Zin_c0、环路增益Tv0以及电流内环的环路增益Ti。因此，根据式（16）可知：

（1）当电压外环控制器Gv增大时，由式（9）可知Tv0增大，由式（12）和式（13）可知Zin_c0增大，但由式（8）可知Ti固定不变，根据式（16）此时不容易定性判断输入阻抗的变化趋势。

（2）当电流内环控制器Gc增大时，Tv0、Zin_c0和Ti均增大，此时不易判断输入阻抗的变化趋势。

（3）当电压采样系数Hv增大时，Tv0和Zin_c0均增大，Ti固定不变，此时不易判断输入阻抗的变化趋势。

（4）当电流采样系数Hi增大时，Tv0和Zin_c0均不变，Ti增大，输入阻抗必将增大。

根据上述分析，讨论其他控制参数固定时，电流采样系数Hi对输入阻抗的影响。当Hi＝0时，输入阻抗最小，此时变换器处于单环控制模式，图5给出了环路增益Tv0、Ti和截止频率之间可能的位置关系，环路增益Tv0的截止频率用fv0表示，电流环环路增益Ti的截止频率用fc表示，随着电流采样系数Hi的增加，fc从fc_1至fc_n方向递增。当电流采样系数Hi从零逐渐增大时，电流内环的环路增益Ti逐渐增大，对应的截止频率fc逐渐提高。

如果fc＜＜fv0，在fc～fv0频率范围内，将有不等式Tv0＞＞1＞＞Ti成立，此时式（16）可化简为

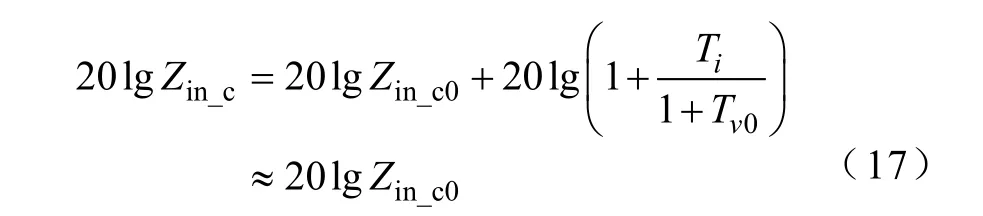
这种情况下，在fc～fv0频率范围内，增大电流采样系数，变换器的输入阻抗逐渐增加，但是变化不大，约等于Zin_c0。

若继续增大Hi使电流环截止频率fc大于fv0时，如图5所示，在fv0～fc频率范围内，一般有Ti＞＞1＞＞Tv0成立，这种情况下，式（16）可化简为

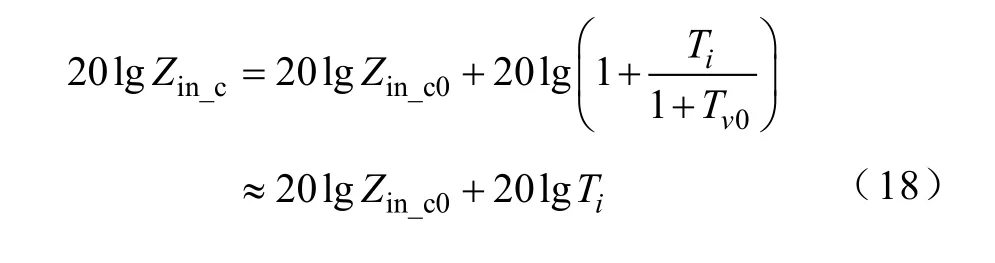
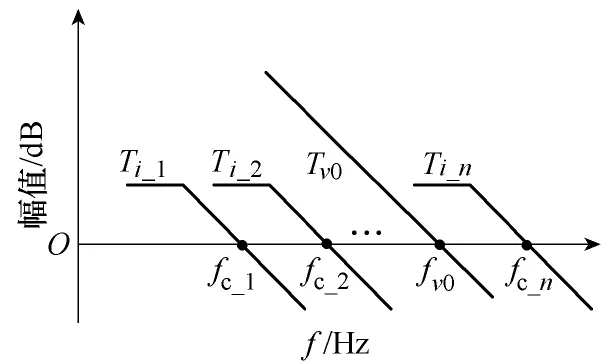
图5　Ti与Tv0的位置关系Fig.5 Position relation between Tiand Tv0

由式（8）可知，如果增大电流采样系数Hi为原来的k倍，则电流内环的环路增益Ti也将变为原来的k倍。根据式（18）可知，电流采样系数增大k倍后的输入阻抗Zi′n_c可表示为

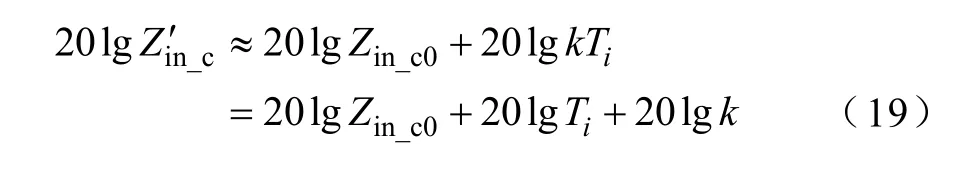
由式（18）和式（19）可知，输入阻抗的增量等于电流内环环路增益的增量。

上述内容是从改善输入阻抗的角度对ICIL控制方法进行的分析，进一步理论分析表明，增大输入电流的采样系数Hi，可有效增大变化器的闭环输入阻抗Zin_c。然而对级联系统中负载变换器的设计，在保证级联系统稳定的基础上，快速性也是设计时需要考虑的主要因素，因此，下文从负载变换器的电压外环响应速度角度进行分析。

1.2 引入ICIL的双环控制方法对电压环的影响

增大输入电流采样系数Hi，将会增大电流内环的环路增益Ti，而不改变Tv0，从而提高变换器的输入阻抗。由式（11）可知，变换器电压外环的环路增益Tv必然减小，截止频率降低，降低了变换器的快速性。这也可从另一个角度进行解释，当级联系统中的负载变换器处于电压外环控制时，在小于电压环截止频率范围内，由于深度负反馈的影响，变换器将体现为恒功率特性，其输入阻抗将表现为负阻特性，与功率相关，约为-Vg2/PL（其中，Vg为输入电压；PL为变换器功率）。当频率大于电压外环截止频率时，变换器的输入阻抗才逐渐偏离负阻特性。因此，如果变换器的电压外环截止频率固定，则在小于截止频率点范围的输入阻抗特性将不易有大的改善。这解释了ICIL双环控制方法在提高电流采样系数时，降低了电压外环环路增益的原因。

综上所述，电流采样系数Hi越大，变换器的输入阻抗也越大。在级联系统中，当前级源变换器的输出阻抗固定时，一般希望后级负载变换器的输入阻抗尽量增大以减少与前级源变换器输出阻抗的交截区。所以，从级联系统的稳定性分析，电流采样系数需要尽量提高；另一方面，电流采样系数Hi越大，会降低变换器电压外环的截止频率，从而影响变换器的快速性。在实际的变换器设计中，往往对级联系统中变换器的截止频率以及级联系统的稳定域度有明确的要求，因此，在实际设计ICIL双环控制的负载变换器时，可综合式（11）、式（18）及式（19）进行输入阻抗Zin_c和电压外环环路增益Tv的设计，进而确定电流采样系数Hi的取值，从而进行稳定性和快速性的折中。本文重点在于改善负载变换器的输入阻抗，提高级联系统稳定性，因此，从稳定性的角度对ICIL双环控制的方法进行实验验证，通过调整电流内环参数Hi，测量变换器的输入阻抗及稳定性。测试变换器输入阻抗的方法如图6所示。图中Ch1和Ch2表示网络分析仪的探头位置，测试输入阻抗用到的电流采样通过0.1Ω电阻实现，即电流采样系数为0.1。利用Ch1和Ch2两点的交流信号电压的比例，即可求得输入阻抗的伯德图[9]。其中，交流正弦信号通过功率放大器传递至隔离变压器一次侧，变压器二次绕组串联接入直流电源，从而产生输入电压的扰动信号。由于变压器的二次绕组流过直流电流，因此变压器需要加入气隙以保证具有一定的抗直流饱和能力，同时要求实验中的变换器输入电流不宜过大。

图6　测试DC-DC变换器输入阻抗的方法Fig.6 Test method for input impedance measurement

2 仿真与实验验证

为验证ICIL双环控制模式下，提高电流采样系数可有效改善负载变换器的输入阻抗，提升级联系统的稳定性，这里将从单变换器和级联系统两方面进行验证。

2.1 单变换器的实验验证

图7为引入ICIL双环控制的Boost变换器原理图，电压环采用比例积分控制器，电流内环采用比例控制器，通过闭环调节实现输出电压恒定。仿真及实验参数见表1。其中，Vm2表示三角调制波的幅值，开关频率100kHz。根据式（16）可知，增大电流采样系数Hi，可增大电流内环的环路增益Ti，而不影响Tv0。这里选用三组电流采样系数，计算并测试变换器的输入阻抗。

图7　采用ICIL双环控制的Boost变换器原理Fig.7 Schematic of Boost converter with ICIL

表1　Boost变换器实验参数Tab.1 Experiment parameters of Boost converter

通过对变换器建模，得到理论计算的电压外环、电流内环的环路增益和输入阻抗分别如图8和图9所示。由图可知，当变换器增大电流采样系数Hi时，其电流内环环路增益Ti逐渐增大，提高了电流内环的截止频率，实现了增大变换器的输入阻抗。

搭建原理如图7所示的实验平台，测试变换器的输入阻抗，以验证上述理论计算结果。受变压器的频率范围限制，测试频率范围为100Hz～10kHz，通过网络分析仪得到三种工况下不同电流采样系数对应的输入阻抗数据，并通过Matlab绘制其输入阻抗曲线如图10所示。与图9相比，测试结果与理论计算结果相吻合。

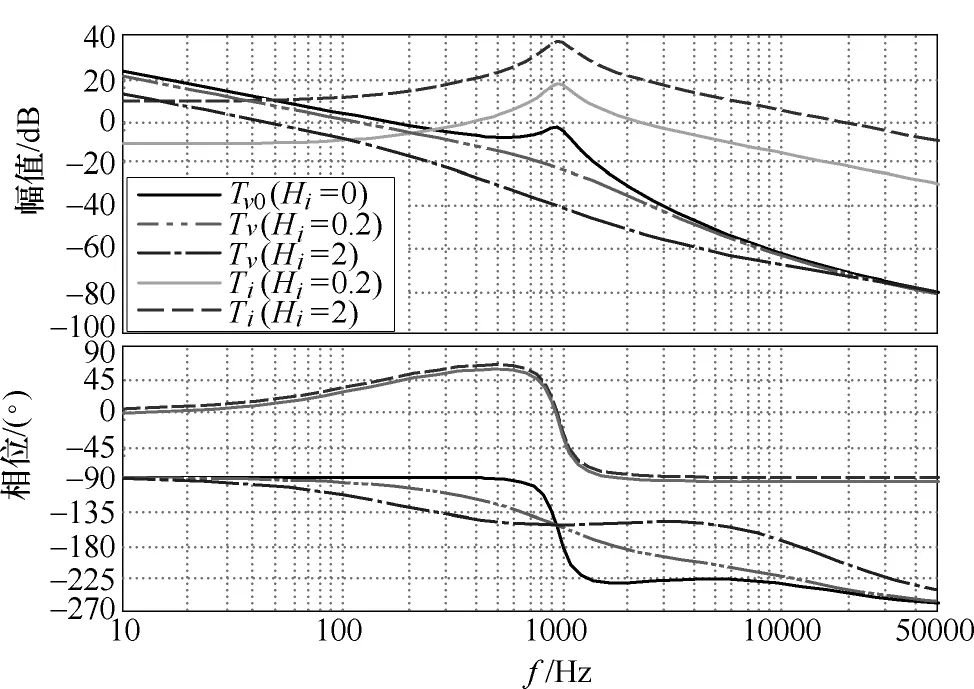
图8　理论计算的环路增益Fig.8 Computed loop gains

图9　理论计算的输入阻抗Fig.9 Computed input impedance

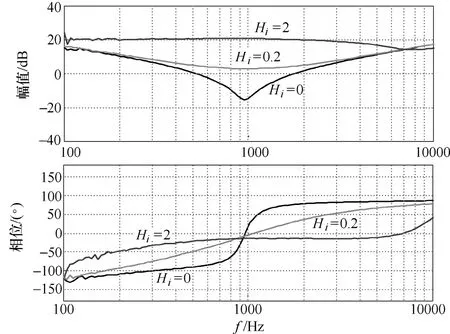
图10　实验测试的输入阻抗结果Fig.10 Test results of the input impedance

2.2 级联系统的仿真与实验验证

采用PSIM仿真软件，搭建原理如图11所示的级联系统仿真平台。其中，级联系统由Buck变换器级联Boost变换器构成，Buck变换器的参数见表2，Vm1表示三角调制波的幅值。Boost变换器的参数见表1。表中电压、电流参数用大写字母表示直流稳态值，开关频率均为100kHz，仿真结果如图12所示。

图11　级联系统原理Fig.11 Schematic of the cascaded system

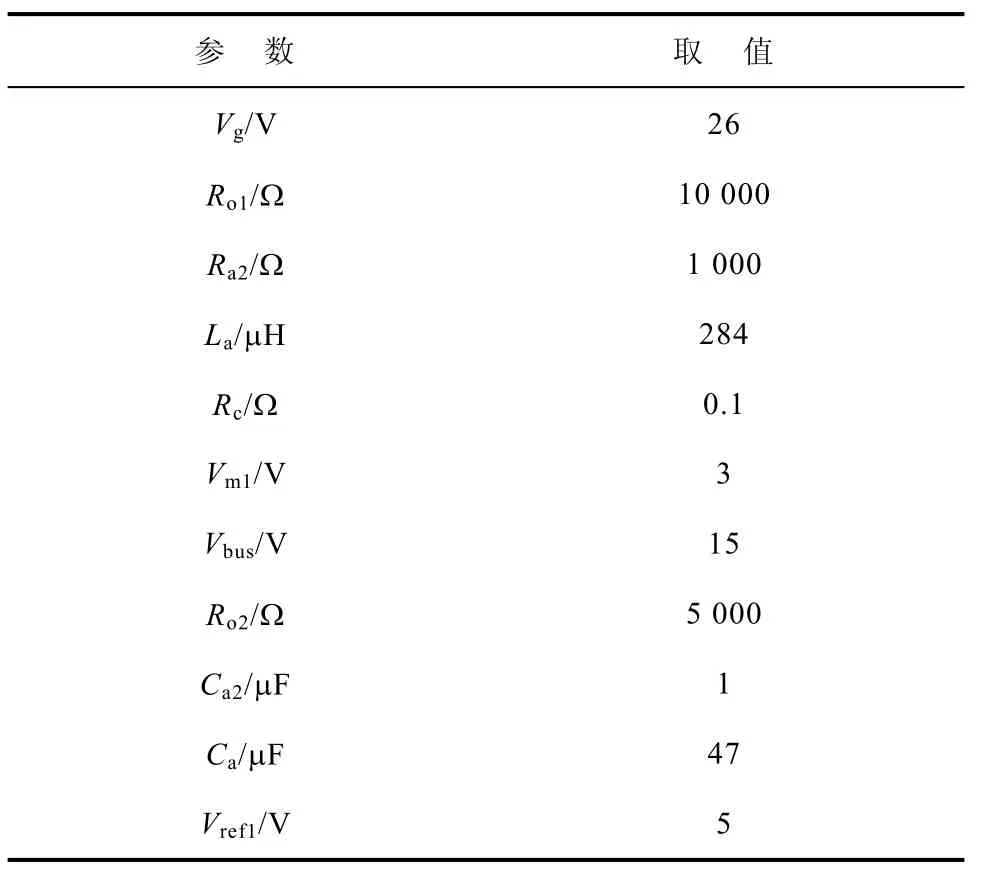
表2　Buck变换器参数Tab.2 Parameters of Buck converter

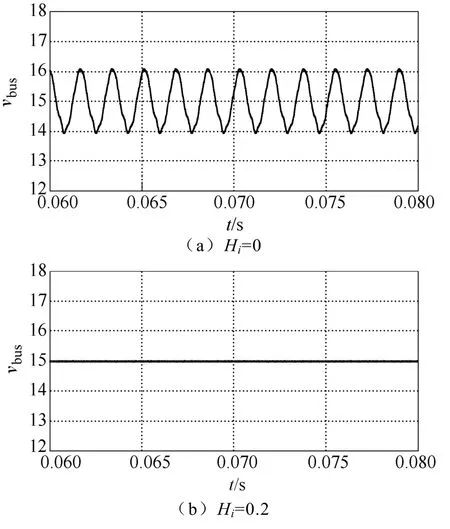
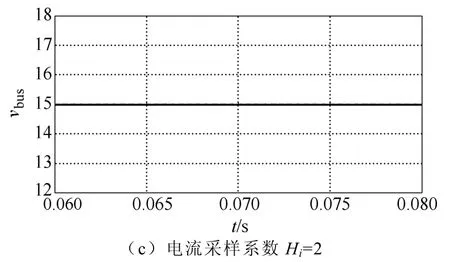
图12　级联系统母线电压仿真结果Fig.12 Simulation results of bus voltage in the cascaded system

由图12可知，当Boost变换器在电流采样系数Hi＝0时，级联系统不稳定，逐渐增大电流采样系数Hi，可使系统趋于稳定。根据表1和表2参数，计算得到Buck变换器的输出阻抗Zout以及Boost变换器的输入阻抗Zin如图13所示，用Matlab根据Zout和Zin计算对应的阻抗比Zout/Zin构成的奈奎斯特曲线和伯德图分别如图14和图15所示。

图13　理论计算的输入、输出阻抗伯德图Fig.13 Computed Bode plots of the input and output impedance

根据传递函数的奈奎斯特曲线和伯德图的关系可知，奈奎斯特曲线与单位圆交点的频率即为伯德图中幅频曲线穿越0dB的频率；奈奎斯特曲线与单位圆的交点距离负实轴的角度，即为伯德图中相频曲线的相位裕度；奈奎斯特曲线与负实轴的交点与（-1，j0）点的距离决定了伯德图中幅频曲线的幅值裕度[10]。

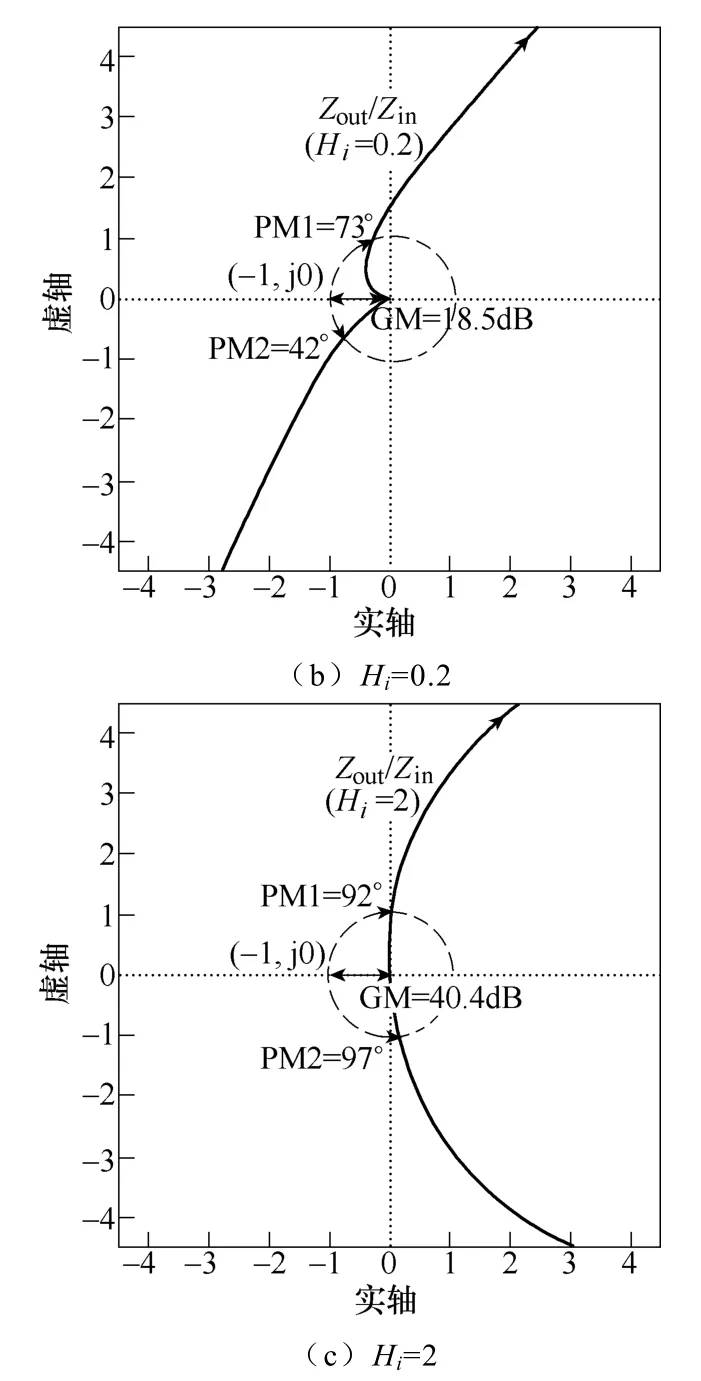
图14　理论计算的阻抗比（Zout/Zin）奈奎斯特曲线Fig.14 Computed Nyquist plots of the impedance ratio（Zout/Zin）

图15　理论计算的阻抗比（Zout/Zin）的伯德图Fig.15 Computed Bode plots of the impedance ratio（Zout/Zin）

由图13～图15可知，当Hi＝0时，在单电压外环的控制下，Boost变换器的输入阻抗Zin与前级Buck变换器的输出阻抗Zout产生大面积的交截区域，阻抗比构成的奈奎斯特曲线包围了（-1，j0）点，级联系统不稳定，此时由于不存在稳定裕度，因此在图14a及图15a中没有标出；当Boost变换器引入输入电流环，Hi＝0.2时，Zin的谐振峰逐渐减小，改善了输入阻抗的阻尼特性，大幅度减少了与前级模块输出阻抗Zout的交截面积，保证了级联系统的稳定；当继续增大电流采样系数至Hi＝2时，Zin的谐振峰值进一步减小，极大程度减小了Zin与Zout间的相互作用，使系统级联逐渐趋于稳定，此时，出现级联系统的阻抗比曲线相交于Hi＝0.2的情况，具有更大的稳定裕度。

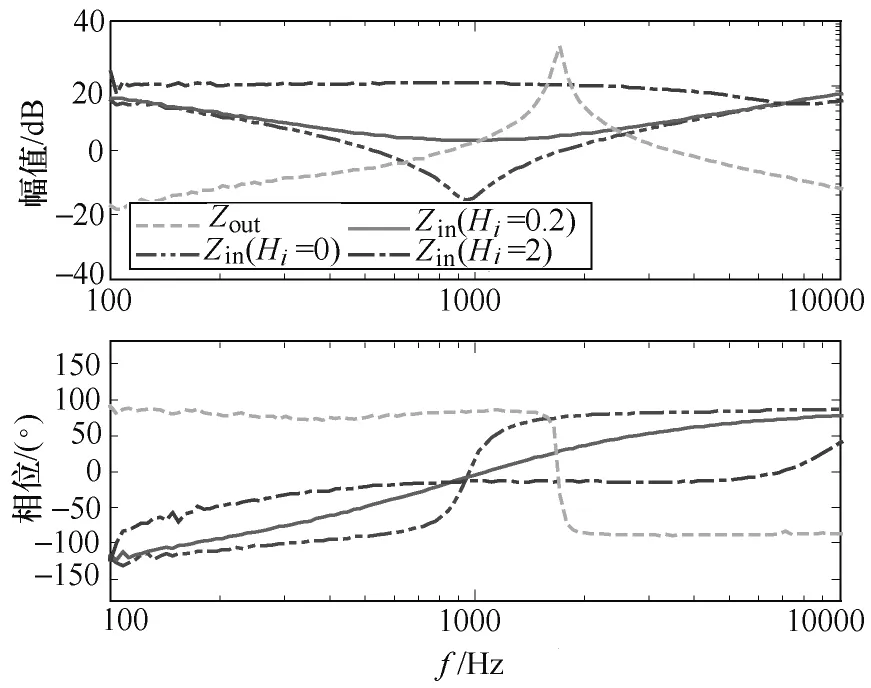
图16　实验测试的输入输出阻抗Fig.16 Test results of input and output impedance

Boost变换器的输入阻抗Zin和Buck变换器的输出阻抗Zout的实验测试结果如图16所示，这与理论计算结果一致（见图13）。搭建如图11所示原理的级联系统实验平台，测试电流采样系数Hi逐渐增大时，变换器级联系统的母线电压vbus（图中为交流分量）、母线电流iLb和Boost变换器的输出电压vout（图中为交流分量），得到实验测试结果如图17所示。

图17　选择不同电流采样系数的级联系统实验波形Fig.17 Experiment results of the cascaded system with different current sampling factors

由图14～图17可知，随着电流采样系数Hi的增大，Boost变换器的输入阻抗随之增大，使其输入阻抗呈现电流性负载的性质，从而消除了Boost变换器输入阻抗中的谐振峰值，改善了其阻尼特性。相应地，随着Boost输入电流采样系数的增大，级联系统中Buck变换器输出阻抗和Boost变换器输入阻抗构成的阻抗比曲线由开始的包含（-1,j0）点逐渐变为不包含（-1,j0）点，说明级联系统从不稳定状态逐渐趋于稳定。另一方面，由图14和图15可知，随着电流采样系数的增大，级联系统的阻抗比曲线的稳定裕度逐渐增大，从而提高了级联系统的稳定性。

3 结论

在级联系统中，源变换器的输出阻抗与负载变换器的输入阻抗是影响级联系统稳定性的重要参数。本文针对DC-DC变换器的小信号模型，提出输入电流内环和输出电压外环的双环控制方法，分析了变换器在双环控制模式下，输入阻抗的构成形式，并得到如下结论：

1）随着内环电流采样系数Hi的增大，变换器的输入阻抗逐渐增大。

2）当电流内环环路增益Ti的截止频率fc大于Tv0的截止频率fv0时，且在fv0～fc频率区间内满足Ti＞＞1，变换器的输入阻抗可大幅度增加，其增量取决于电流内环的环路增益Ti的增量。

3）通过增大电流采样系数，提高电流内环的环路增益，可有效改善变换器的输入阻抗中存在的谐振峰值，使变换器的输入阻抗体现良好的阻尼特性，从而增加阻抗比曲线的稳定裕度，提高级联系统的稳定性。

本文分析了输入电流内环参数对变换器输入阻抗的影响，以及对变换器反馈控制系统设计的闭环控制系统的影响，得到了对于双环控制系统下变换器的稳定性和快速性之间的关系。同时，本文指出输入电流内环参数能够影响输入阻抗的本质是在一定频率范围内将负载变换器的负阻特性改变为恒流特性，从而减小了级联系统中前后级模块的阻抗交截范围。最后，通过单变换器和级联系统中进行的仿真及实验，验证了该控制方法的有效性。

参考文献

[1]Liu Xinyun,Forsyth A J,Cross A M.Negative input-resistance compensator for a constant power load[J].IEEE Transactions on Industrial Electronics,2007,54（6）:3188-3196.

[2]Spiazzi G,Pomilio J A.Interaction between EMI filter and power factor preregulators with average current control:analysis and design considerations[J].IEEE Transactions on Industrial Electronics,1999,46（3）:577-584.

[3]Spiazzi G,Rossetto L,Pomilio J.Analysis of EMI filter induced instabilities in Boost power factor preregulators[C]//29th IEEE Annual Power Elec-tronic Specialists Conference,1998,2:1048-1053.

[4]Erickson R W.Fundamentals of power electronics[M].Springer Netherlands:Kluwer Academic Publishers,2000.

[5]Zhang X,Ruan X,Kim H.Adaptive active capacitor converter for improving stability of cascaded DC power supply system[J].IEEE Transactions on Power Electronics,2013,28（4）:1807-1816.

[6]Abe S,Hirokawa M,Ninomiya T.Output impedance design consideration of three control schemes for bus converter in on-board distributed power system[C]//International Conference on Power Electronics and Drive Systems,2007:1388-1393.

[7]Abe S,Hirokawa M,Shoyama M.Optimal bus capacitance design for system stability in on-board distributed power architecture[C]//Power Electronics and Motion Control Conference,2008:393-399.

[8]Abe S,Hirokawa M,Zaitsu T.Design consideration of full-regulated bus converter for system stability of on-board distributed power system[C]//International Symposium on Power Electronics,Electrical Drives,Automation and Motion,2006:629-633.

[9]Panov Y,Jovanovic M.Practical issues of input/output impedance measurements in switching power supplies and application of measured data to stability analysis[C]//Twentieth Annual IEEE Applied Power Electronics Conference and Exposition,2005,2:1339-1345.

[10]Wildrick C M,Lee F C,Cho B H.A method of defining the load impedance specification for a stable distributed power system[J].IEEE Transactions on Power Electronics,1995,10（3）:280-285.

王 剑 男，1979年生，博士，讲师，研究方向为并网变流器控制策略和大功率电能变换技术。

E-mail:jwang4@bjtu.edu.cn

贾鹏宇 男，1985年生，博士研究生，主要研究方向为直流电源系统稳定性。

E-mail:08117338@bjtu.edu.cn（通信作者）

Input Current Inner Loop Control Method to Increase the Input Impedance of Load Converters

Wang Jian Jia Pengyu Li Yan Zheng Qionglin Guo Xizheng
（School of Electrical Engineering Beijing Jiaotong University Beijing 100044 China）

AbstractTo improve the stability of cascading system,the intersection range of output impedance and input impedance should be decreased.That is,the output impedance of source converter should be decreased,while the input impedance of load converter should be increased.Based on the unified small signal model of DC-DC converter,the double loop control method with input current inner loop（ICIL）and output voltage outer loop is proposed.The input impedance is analyzed under this situation,and the quantization calculation process of the input impedance is provided when the current sampling factor is changed.It is shown that when the cross-over frequency of the current loop is larger than that of the voltage loop,the input impedance increases significantly as the current sampling factor increases.Therefore the impedance intersection of source and load converters will be decreased to improve the stability.

Keywords：Cascaded system,DC-DC converter,input impedance,input current,stability

作者简介

收稿日期2013-12-03 改稿日期 2014-04-14

中图分类号：TM46