面向环境变化监测的天线传感器仿真分析
张菡玫

摘 要:【目的】为了精确检测出固体材料内的环境变化,设计出一种完全开放的、埋于被测材料中的天线传感器,并在此基础上设计出一个可监测环境内各种元素变化的传感器。【方法】利用有限元法来计算天线的输入阻抗,通过建模推导出传感器的灵敏度方程,并进行仿真分析。通过调整天线旁圆柱体的距离和高度来模拟真实环境变化,验证天线传感器对周围环境进行监测的灵敏性。【结果】当圆柱体距离天线传感器在0~50 mm范围内不断移动,且改变圆柱体高度时,圆柱体高度越高,共振就越小,此时的磁场E越大,频率区间的反射系数越大。【结论】由仿真结果可知,天线传感器可测量较近环境(0~50 mm)的变化情况。当圆柱体距离天线传感器位置越近,且高度越高时,灵敏度值就越大,此时监测环境变化的情况就越精确。
关键词:天线传感器;有限元法;灵敏度;输入阻抗
中图分类号:TN821 文献标志码:A 文章编号:1003-5168(2024)04-0014-05
DOI:10.19968/j.cnki.hnkj.1003-5168.2024.04.003
Simulation Analysis of Antenna Sensor for Environmental Change Monitoring
ZHANG Hanmei
(Wuchang Polytechnic College, Wuhan 430000, China)
Abstract:[Purposes] In order to accurately detect environmental changes within solid materials, a completely open antenna sensor embedded in the material being measured is designed, and on this basis,it designs and simulates a sensor that can monitor changes in various elements in the environment. [Methods] The finite element method is used to calculate the input impedance of antennas, and the sensitivity equation required by the sensor is derived through modeling and simulated. Adjust the distance and height of the cylinder next to the antenna to simulate real environmental changes and verify the sensitivity of the antenna sensor in monitoring the surrounding environment. [Findings] When the cylinder is continuously moved within the range of 0~50 mm from the antenna and the height of the cylinder is changed at the same time, the higher the height of the cylinder, the smaller the resonance, the greater the magnetic field E, the greater the reflection coefficient in the frequency range. [Conclusions] After simulation can be that the antenna can measure changes of 0~50 mm in the nearby environment. When the cylinder is closer to the antenna position and the height is higher, the sensitivity value obtained is greater. When the sensitivity value is greater, it indicates the more accurate it is to monitor changes in the environment.
Keywords: antenna sensor; finite element method; sensitivity; input impedance
0 引言
傳统电磁传感器的换能装置是固有的,因此,传感器的价格便宜,且生产相对简单。传统的高频电磁波谐振腔传感器能非常精确地测量出腔体的谐振频率及其阻尼系数,但这类传感器需要将待测材料封闭在外壳中,且高次模式的谐振腔容易受谐振频谱密集及模式竞争现象的影响,导致其性能发挥受限,而开放式谐振腔在一定程度上改善了这些问题[1]。在带有开放式谐振腔的测量系统中,其开放式谐振腔的侧面与被测材料接触,但被测材料与测量装置界面之间的杂质可能会使测量产生很大偏差[2]。因此,本研究设计出一种完全开放、埋于被测材料中的电磁传感器,并通过识别传感器的影响参数来绘制灵敏度图。
本研究在理论分析基础上,设计出小材料天线传感器,再对传感器尺寸进行调整,并进行一系列的试验测试,通过模拟环境变化来验证天线传感器的灵敏度特性。
1 原理分析
本研究所使用的传感器主要由天线组成,而各类天线的输入阻抗特性不相同,且不同天线之间相差较大[3]。输入阻抗是天线向介质发射能量的能力特征,为了能最大限度发挥天线优势,提高发射效率和覆盖效果,本研究对天线输入阻抗进行有限元计算。
1.1 有限元法
有限元法是一种用于近似求解数理边值问题的数值方法,基于伽辽金检验,得到波动方程弱形式,并在指定边界条件下求解电磁场的解。在电磁数值计算领域中,该方法被广泛应用于求解微分方程边界问题[4]。本研究设计的通用天线如图1所示,天线由电流密度为J的电流源激励。在描述复杂媒介时,使用张量形式介电常数[ε]和磁导率[μ]来表示各异性媒介参数。
为了解决边值问题,使用伽辽金方程,并基于高斯定理及柯西边界条件[5],见式(1)。
[vrotT·μ?1r·rot(E)?k20TεrEdV=s0∪specn·[T×(μ-1r·rot(E))]dS-vT·jk0Z0JdV] (1)
式中:E为矢量电场;T为加权函数;[μr]为张量形式的磁导率;[εr]为张量形式的介电常数;[k0]为自由空间中的波数;j为虚数单位。
1.2 输入阻抗计算
为了计算出输入阻抗,分为两种情况进行考虑。
1.2.1 电流源。当使用电流源时,已知电流I的值,可计算出电流密度J,并利用方程[V=?abEdl]推导出体积V中各处的电场E,从而计算出a和b之间的电压[U],并得到天线的输入阻抗[z=UI] 。
1.2.2 电压源。当使用电压源时,已知电压V的值,且假设a和b之间的电场E是均匀的。因此,可利用式(2)计算电流密度J。
[rotμ?1r×rotE?k20εrE= ?jk0Z0J] (2)
式中:[μr]为真空磁导率常数;[εr]为真空介电常数;[k0=ωμ0ε0],[Z0=μ0ε0]。
2 偶极子天线建模
偶极子天线是由Heinrich Rudolph Hertz于1886年左右开发出的,是一种由金属绞线组成的天线,由一对对称放置的导体构成,导体相互靠近的两端分别与馈电线相连,主要用于发射或接收电磁能[6]。
2.1 模型化
通过天线建模,可推导出天线尺寸变化的参数表达式。在设计天线系统时,需要获得系统的介电常数[ε]、电导率[σ]和磁导率[μ],如果天线不固定,也可推导出位移参数,见式(3)。
[vEA×fEBdV=vEB×fEAdV] (3)
式中: [EA]、[EB]为电场;[fEB]、[fEA]为电压源作为电场E的函数。
2.2 灵敏度方程
为了得到灵敏度的表达式,在电压源下对2种不同状态进行建模。在状态A1中,假设天线使用的是电压源V,且结构包括任意介电常数的材料,电场可通过电压密度来计算。在状态 A2 中,介电常数发生变化,对这两种状态进行微分。状态A如图2所示。
在状态B下,设置电压V=d,且其他参数条件已知时,设置材料空间的电场[E= -1]。状态B如图3所示。
通过状态A、B,结合高斯函数,可推导出灵敏度方程,见式(4)。
[δIδεr= ?Ajωε0dξ2dvavecA=Eξ] (4)
式中:E为矢量电场;[ξ]为环境变化参数;[d]为距离参数;[ε0]为自由空间介电常数;j为虚数单位;[ω]为角频率。
3 偶极子天线仿真
在得到理论方程后,需要进行仿真对比。在进行仿真时,需要关注的参数有输入阻抗和反射系数。本研究使用HFSS软件来计算该参数,利用反射系数结果来测量不同环境条件下共振的变化。当维持谐振时,需要将计算出的输入阻抗和理论值进行比较,验证理论结果的可靠性。
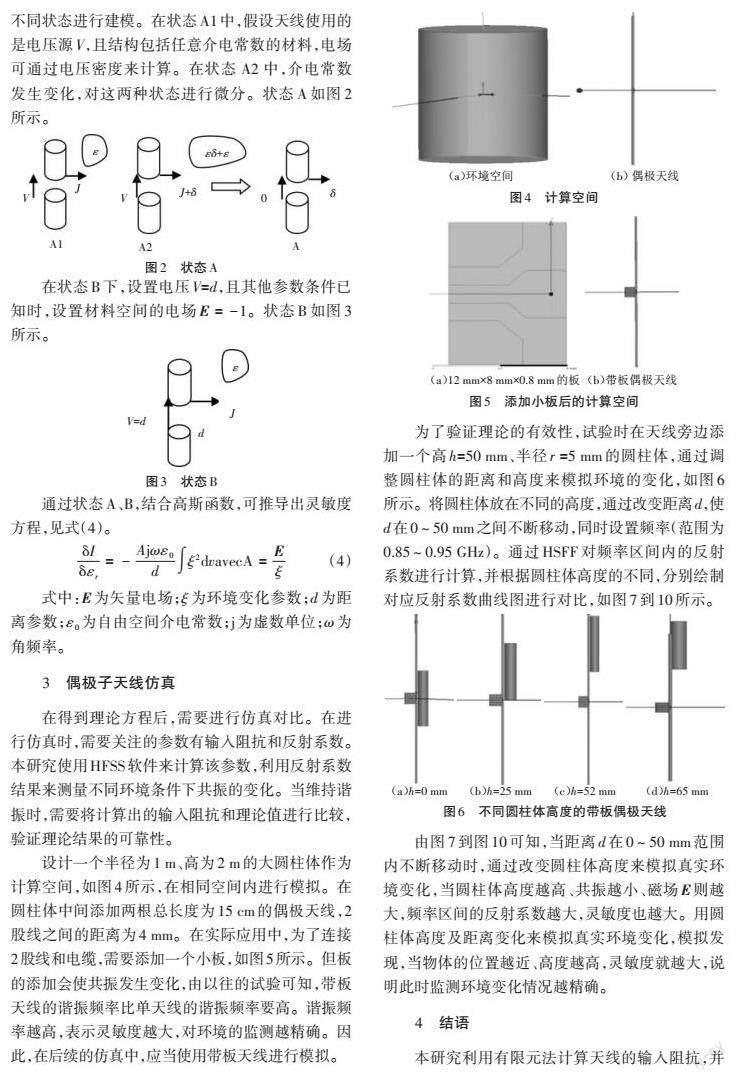
设计一个半径为1 m、高为2 m的大圆柱体作为计算空间,如图4所示,在相同空间内进行模拟。在圆柱体中间添加两根总长度为15 cm的偶极天线,2股线之间的距离为4 mm。在实际应用中,为了连接2股线和电缆,需要添加一个小板,如图5所示。但板的添加会使共振发生变化,由以往的试验可知,带板天线的谐振频率比单天线的谐振频率要高。谐振频率越高,表示灵敏度越大,对环境的监测越精确。因此,在后续的仿真中,应当使用带板天线进行模拟。
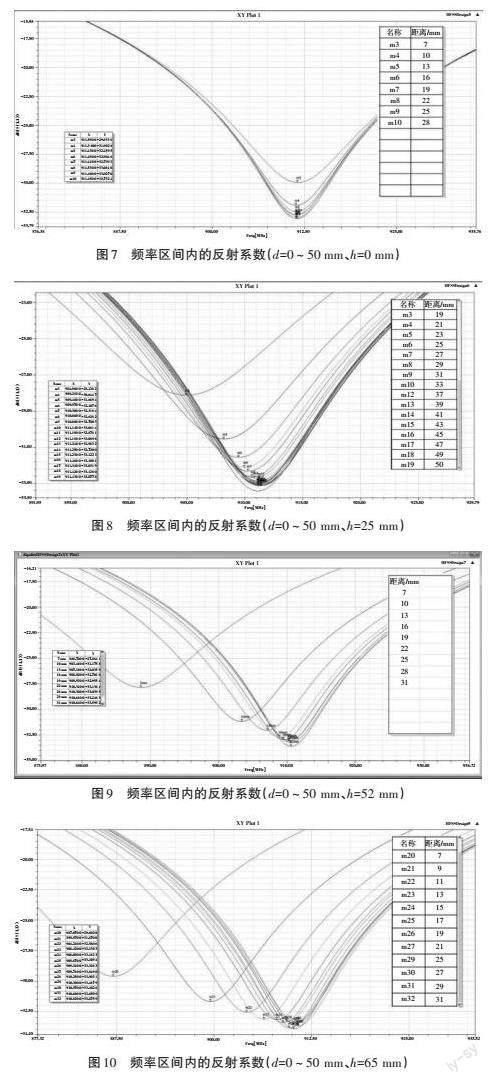
为了验证理论的有效性,试验时在天线旁边添加一个高h=50 mm、半径r =5 mm的圆柱体,通过调整圆柱体的距离和高度来模拟环境的变化,如图6所示。将圆柱体放在不同的高度,通过改变距离d,使d在0~50 mm之间不断移动,同时设置频率(范围为0.85~0.95 GHz)。通过HSFF对频率区间内的反射系数进行计算,并根据圆柱体高度的不同,分别绘制对应反射系数曲线图进行对比,如图7到10所示。
由图7到图10可知,当距离d在0~50 mm范围内不断移动时,通过改变圆柱体高度来模拟真实环境变化,当圆柱体高度越高、共振越小、磁场E则越大,频率区间的反射系数越大,灵敏度也越大。用圆柱体高度及距离变化来模拟真实环境变化,模拟发现,当物体的位置越近、高度越高,灵敏度就越大,说明此时监测环境变化情况越精确。
4 结语
本研究利用有限元法计算天线的输入阻抗,并通过建模来推导出传感器需要的灵敏度方程。通过调整天线旁圆柱体的距离和高度来模拟真实环境变化,从而可以验证天线传感器对于周围环境进行监测的灵敏性。由仿真结果可知,天线可测量较近环境(0~50 mm)的变化情况,当圆柱体距离天线位置越近,且圆柱体高度越高时,获得的灵敏度值就越大;而当灵敏度值越大,表示此时监测环境变化情况越精确。
参考文献:
[1]郭炜.一种新型模式选择开放腔的研究[D].北京:中国科学院研究生院(电子学研究所),2006.
[2]李云飛,韩国栋,王鸣杰,等.面向结构裂纹监测的贴片天线传感器技术研究进展[J].起重运输机械,2023(13):64-70.
[3]袁军,卢光辉.中波发射天线输入特性阻抗分析与选频设计[J].广播与电视技术,2019(7):103-108.
[4]LUO G Q,HONG W,LAI Q H,et al.Frequency-selective surfaces with two sharp sidebands realized by cascading and shunting substrate integrated waveguide cavities[J].IET Microwaves,Antennas & Propagation,2008(1):23-27.
[5]巢俊杰.面向周期电磁结构的频域有限元方法研究及其应用[D].西安:西安电子科技大学,2022.
[6]JIN J M.The Finite Element Method in Electromagnetics[M].New York:Wiley,2002.

