AFM轻敲模式下扫描参数对成像质量影响的研究
陈建超, 安小广, 冯世绪, 王加春
(1.燕山大学 机械工程学院,河北 秦皇岛 066004;2.河北省重型智能制造装备技术创新中心,河北 秦皇岛 066004)
1 引 言
随着微/纳米技术的发展,原子力显微镜(atomic force microscopy, AFM)已被广泛地用于表征微纳结构(微裂纹、微沟槽)和表面的微观几何形貌等[1~10]。虽然原子力显微镜最高能达到纳米级的纵横向分辨率,但不合理的扫描参数(如扫描频率、积分增益、扫描振幅等)设置会引入反馈系统控制误差,从而降低测量精度[11]。
近年来,相关学者已开展了轻敲模式下扫描参数对成像质量的影响研究。Sulchek T等[12]通过推导得出探针扫描上升沿的幅值误差与扫描频率呈线性关系;Kodera N等[13]发现减小幅值设定点有助于增大反馈带宽;Su等[14]发现减小幅值设定点可以提高探针误差增长率;薛勃等[15]研究了扫描频率、积分增益、扫描振幅分别对成像质量的影响规律,得出扫描频率、积分增益及扫描振幅三者决定了AFM闭环系统在工作时对输入信号响应的程度。但这些研究均局限于单一扫描参数对成像质量的影响分析,没有考虑扫描参数之间是否存在耦合影响。而AFM作为一个误差驱动的闭环控制系统,其反馈增益(积分增益、比例增益)的优化依赖于幅值误差(幅值设定点与探针幅值的差值)的大小,而探针幅值又受反馈增益的影响。由此可见AFM扫描参数之间存在明显的耦合效应。
因此,本文在确立合理的AFM成像质量评价指标的基础上,研究了扫描参数对成像质量的影响规律以及对成像质量的耦合作用,为AFM扫描参数的合理选择提供重要的参考依据。
2 成像质量评价依据与实验方法
2.1 成像质量评价依据
AFM的工作原理实质上就是一个闭环控制系统,如图1所示。

图1 AFM闭环控制系统示意图Fig.1 Schematic diagram of closed loop control system of AFM
样品表面形貌变化引起高频振动探针的振动幅值发生变化,而光杠杆能够实时检测探针振动的幅值。在扫描范围内的样品表面上任意一点,光杠杆检测得到的探针振动幅值作为反馈信号与系统设定幅值(幅值设定点)进行比较产生误差信号(幅值误差)[16,17]。该信号经过PI放大器(比例增益、积分增益)的放大,控制压电陶瓷扫描管沿竖直方向运动,使针尖与样品之间的幅值维持在设定幅值,扫描管的位移量即该点的绝对高度值。可见,该点的幅值误差越小压电陶瓷扫描管越能够更准确的记录该点的形貌高度值。因此,可依据幅值误差来表征成像质量的优劣,幅值误差逾小则精度逾高。
针对如何用三维的幅值误差信息去表征三维的表面形貌,进行了大量的实验,对两类不同类型的表面采用了相应的评价策略。
对于周期表面(如台阶结构),AFM探针扫描经过台阶两侧边缘位置时,由于台阶边缘位置高度值变化很大,引入的幅值误差明显高于台阶的其他位置。如图2所示,正的幅值误差是由探针扫描台阶边缘的下降沿(自上而下扫描)产生,负的幅值误差是由探针扫描台阶边缘的上升沿(自下而上扫描)产生。评价AFM成像的优劣可采用幅值误差的峰值(幅值误差的绝对值)为评价指标。

图2 标准台阶轮廓以及对应的幅值误差图Fig.2 Standard step outline and corresponding amplitude error drawing
不同于台阶标样,随机表面形貌特征更加复杂,更具有一般的代表性,如图3所示。

图3 随机表面形貌以及对应的幅值误差图Fig.3 Random surface morphology and corresponding amplitude error drawing
幅值误差图为了反映整个样品表面的成像质量就不能单独取某一细节的幅值误差来表征。因此为了体现幅值误差的整体统计结果,需要定义评价指标表示幅值误差。在三维表面粗糙度评价参数中,表面算术平均偏差Sa和表面十点高度Sz能够很好地反映随机表面三维形貌整体情况以及极值分布情况,所以借鉴这2个参数定义了随机表面的幅值误差图的2个评价指标——幅值误差算术平均误差Eq和幅值误差10点高度Ez:
(1)
(2)
式中:M为快扫(x)方向的采样点数;N为慢扫(y)方向的采样点数;e(xi,yj)为各个采样点处的幅值误差;esi为峰值采样点处的幅值误差;evi为谷值采样点处的幅值误差。
2.2 实验方法
实验使用布鲁克Dimension Icon型原子力显微镜,配备弹性系数为42 N/m的轻敲探针(TESPA,针尖曲率半径为10 nm)。被测样品包括带有周期性表面的标准台阶(VGRP-15,台阶高183 nm,宽 4.5 μm,制造误差为±1%)和随机表面的聚二甲基硅氧烷膜(PDMS-SOFT-1)。本文重在评估AFM闭环控制系统控制探针跟踪样品表面的响应能力,通过限制每根探针扫描图幅的数量保持针尖的锋利度,使“扩宽效应”对样品表面形貌测量的影响维持在较低且相近的水平。从而避免针尖(包括适度磨损的状态下)几何尺寸的“扩宽效应”对所测数据造成影响。实验在大气环境下(室温20~25 ℃)进行。针对周期性表面,首先采用单因素实验法,控制单一扫描参数变量,在同一位置上扫描3次(扫描中若出现疑似污染物导致重影问题,采用更换探针的方法继续完成该组参数的扫描任务,以避免引入针尖受污染后带来的测量假象),且每次以不同频率扫描,获取单一变量下成像质量的变化规律;针对随机表面,采用双因素实验法,将扫描参数两两组合,以每组参数中的其中一个参数作为单一变量,在同一位置上扫描3次,每次还要以另一扫描参数的不同设定值进行扫描,获取在这一变量下成像质量的变化规律,分析这2个扫描参数之间是否存在耦合作用,若存在,则可进一步获取耦合作用对成像质量的影响规律。
3 扫描参数对标准台阶表面成像质量的影响分析
本文对积分增益I、比例增益P、扫描频率fs、幅值设定点S这4个扫描参数对标准台阶成像质量的影响进行了研究。采用单因素实验法,实验设计参数如表1所示,表中自变量指以确定位置对应的扫描参数作为自变量。

表1 扫描台阶标样时的参数设置Tab.1 Scanning parameter settings for standard step surfaces
按照表1的实验设计完成实验,并依据第2节所述数据处理和评价方法,获得扫描参数对成像质量的影响关系曲线,如图4~图7所示。
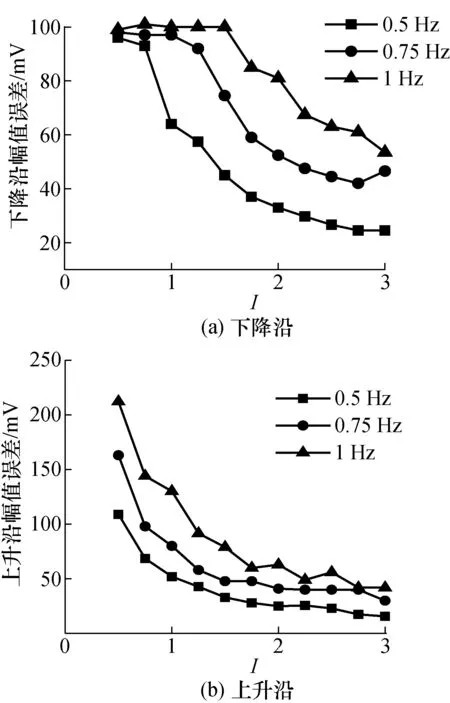
图4 幅值误差与I的关系图Fig.4 The relationship between amplitude error and I
图4为幅值误差与I的关系曲线,在台阶下降沿,随着I增大,幅值误差先保持不变,随后逐渐减小;在台阶上升沿,随着I增大,幅值误差逐渐减小;降低扫描频率,两者的幅值误差都减小。说明增大I、降低fs可以减小幅值误差,提高成像质量。
幅值误差与P的关系曲线如图5所示。在台阶下降沿和上升沿随着P增大,幅值误差的变化趋势并不明显,这说明P对提高成像质量的影响并不大。

图5 幅值误差与P的关系图Fig.5 The relationship between amplitude error and P
幅值误差与fs的关系曲线如图6所示。上升沿和下降沿的幅值误差都随着fs的增大而增大,台阶上升沿的幅值误差呈近似线性上升趋势;这与文献[12]理论推导得出的探针扫描上升沿幅值误差与扫描频率呈线性关系的结论相一致,从侧面也验证了论文评价方法和实验的合理性,也揭示出降低fs可以提高成像质量。
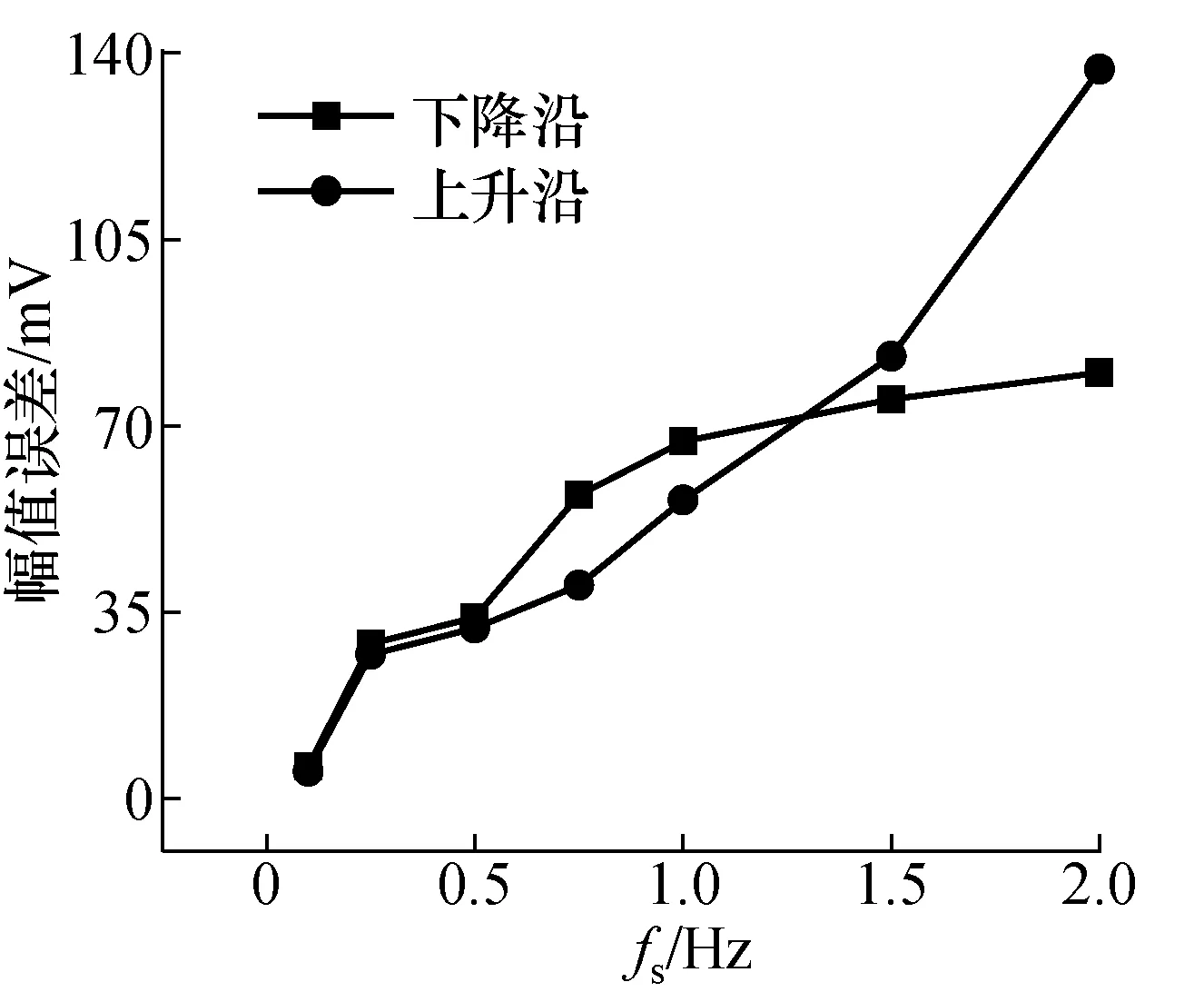
图6 幅值误差与fs的关系图Fig.6 The relationship between amplitude error and fs
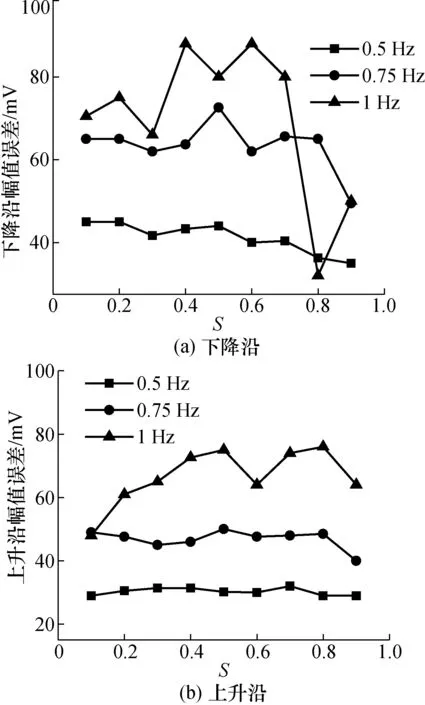
图7 幅值误差与S的关系图Fig.7 The relationship between amplitude error and S
图7为幅值误差与S影响关系曲线,可以看到当以1.0 Hz的速度扫描时,台阶下降沿的幅值误差在S=0.8位置断崖式下降前呈现随设定点增大而震荡上升的趋势,相对地台阶上升沿幅值误差则在0.1~0.5设定点区间稳步上升,随后在0.5~0.9设定点区间小幅度震荡。因此从整体上看,高扫描频率(1.0 Hz)下幅值误差尚存在随着S的增大而增大的趋势。以低速扫描时,幅值误差在下降沿随着S的增大而减小。在上升沿S对幅值误差的影响规律并不明显。说明当fs较大时,减小S可提高成像质量。当S=0.9,fs分别为0.75 Hz和1 Hz时,下降沿幅值误差降至50 mV,等于探针幅值饱和值,这是由于探针脱离样品表面自由振动引起的,并不能说明此时成像质量优良。
从图4中还可以发现,fs对I的选择有明显的影响,在保证扫描质量的前提下,以低速扫描时,I有更宽的选择区间。说明I与fs之间存在耦合影响。为进一步验证这一发现,有必要研究扫描参数对成像质量的耦合影响。
4 扫描参数对随机表面成像质量的影响分析
针对随机表面,实验重点观察各参数之间的耦合作用对成像质量的影响规律。因P对成像质量的影响并不明显,故实验因素仅考虑I、fs和S3个参数。实验参数设置如表2和表3所示,表中变量1和变量2分别表示以确定位置对应的扫描参数作为第1变量和第2变量。

表2 扫描随机表面的参数设置Tab.2 Scanning parameter settings for random surfaces
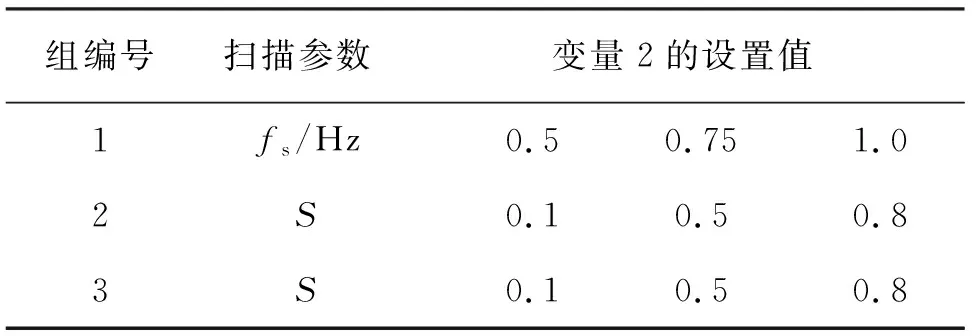
表3 表2中各组内变量2的参数设置Tab.3 Parameter setting of the second variable in Tab. 2
按照表2和表3的实验设计完成实验,获得结果如图8~图11所示。
图8为S=0.8时幅值误差与I的关系曲线,可以看出随着I的增大,幅值误差先逐渐减小,后又逐渐开始增大。这是由于随着I的增大,系统响应加快能够有效地降低稳态误差,从而降低幅值误差。但当I过大时会导致系统发生自激振荡效应,从而引起幅值误差变大。因此,在测量时应选择适当的I值,避免系统出现自激振荡而引入额外的测量误差。此外,曲线也表现出I的选择受fs的影响,出现自激振荡现象的I值随fs的减小而增大。fs和I之间存在明显的耦合关系。

图8 S=0.8时幅值误差与I的关系图Fig.8 The relationship between amplitude error and I when the S=0.8
图9为不同S情况下,fs=2 Hz时I对幅值误差的影响曲线,可发现随着I的增大,幅值误差先逐渐减小,后又逐步增大。

图9 fs=2 Hz时幅值误差与I的关系图Fig.9 The relationship between the amplitude error and the I at fs=2 Hz
随着S减小,最佳I值逐渐增大且产生更低的幅值误差。S=0.1时,I>5才发生自激现象。S与I之间也存在明显的耦合关系。
同样在不同S情况下,fs对幅值误差的影响如图10所示,可以看出随着fs增大,幅值误差逐渐增大,但是S较低时幅值误差缓慢增大,在3.5 Hz时才会出现自激现象,而S=0.8时fs增大到1 Hz就出现自激现象。S较低时,fs与S之间没有明显的耦合关系,而S较高时,fs与S之间的耦合关系比较明显。
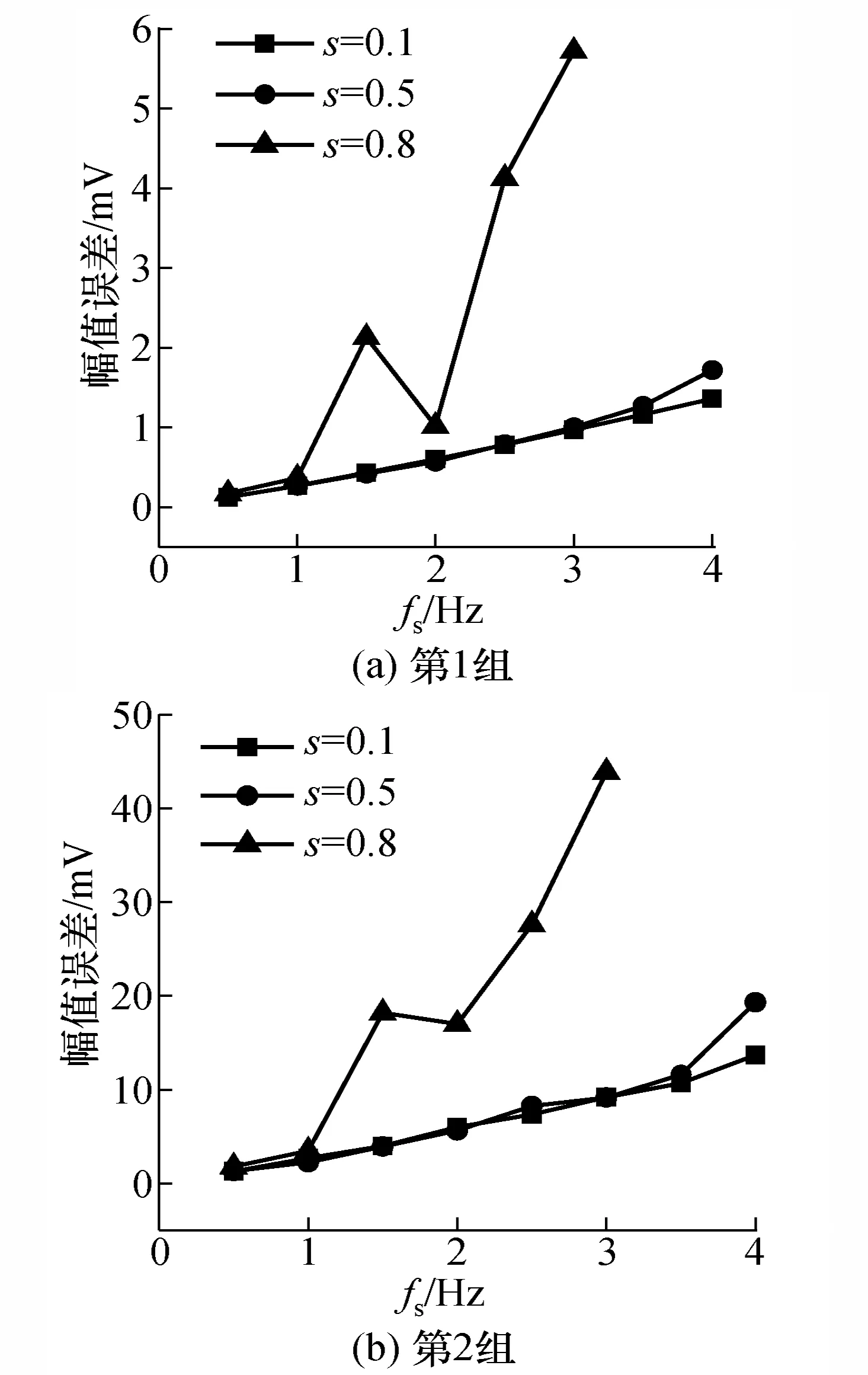
图10 幅值误差与fs的关系图Fig.10 The relationship between amplitude error and fs
横向对比图8(第2组实验)和图9(第2组实验)可发现,图9中fs=2 Hz时的幅值误差与图8中第2组实验中fs=0.5 Hz时的最小幅值误差相当。这说明减小S能够进一步提高fs而不增大幅值误差。为了进一步说明这个问题,将fs提高到3 Hz,得到S=0.1时幅值误差与I的关系图如图11所示。

图11 S=0.1时幅值误差与I的关系图Fig.11 The relationship between amplitude error and the I at S=0.1
从图11中可以看到当I增大至4时,fs=3 Hz设置下产生的幅值误差相比于fs=2 Hz设置下的虽有所增大,但仍低于第1组中S=0.8,fs=1 Hz设置下产生的最小幅值误差。证明了在低幅值设定点下,可以适当提高扫描频率而不会明显增大幅值误差、降低成像质量。
5 结 论
本文以幅值误差作为评价AFM成像质量优劣的指标,通过实验得到了扫描参数对成像质量的影响规律以及扫描参数之间的耦合作用对成像质量的影响规律,对实验结果的进一步分析得出:
(1) 对成像质量影响最大的扫描参数是fs和I, 减小fs, 适当增大I可以显著降低幅值误差,提高成像质量;P对成像质量基本没有影响;在一定范围内,适当减小S,可降低幅值误差,提高成像质量。
(2) 扫描参数I、fs、S两两之间存在耦合影响。
(3)fs设置为较小值时,I有更宽的选择区间以维持较低的幅值误差;S设置为较小值时可允许设置更大的I和fs以维持较低的幅值误差,从而实现高效高质量的表面测量。

