基于频域相位信息的声表面波谐振器回波频率估计
李亚飞, 陈智军,2, 朱卫俊, 黄鸿伟, 熊志强
(1. 南京航空航天大学 自动化学院,江苏 南京 211106; 2.南京航空航天大学高速载运设施的无损检测和监控技术工信部重点实验室,江苏 南京 211106;3.中电科技德清华莹电子有限公司,浙江 德清 313200)
1 引 言
声表面波谐振器(surface acoustic wave resonator, SAWR)可作为传感器使用,对SAWR回波信号载波频率的精确估计是实现精确传感的前提[1]。目前估计SAWR回波频率的方法可分为扫频法[2]和频域变换法[3, 4]2种。扫频法采用扫频测强度的方式,测量速度慢、测量周期长。频域变换法采用快速傅里叶变换(fast Fourier transform, FFT)方法,但频谱分辨率有限。相关文献在FFT基础上提出了Rife插值[5]、抛物线插值[6]等改进算法。当SAWR谐振频率处于FFT幅度谱中峰值谱线频率附近时,Rife插值算法的频率估计精度将大幅度降低[7]。与之相反,当SAWR谐振频率远离FFT峰值谱线时,抛物线插值算法的精度将降低[8]。
本文提出了一种基于频域相位信息的SAWR回波信号频率估计算法。在推导算法的基础上,通过SAWR无线测试系统和仿真回波信号对该算法的性能进行了验证,表明了该算法的有效性。
2 回波信号
SAWR由压电基底、叉指换能器(interdigital transducer, IDT)与反射栅组成,如图1所示。
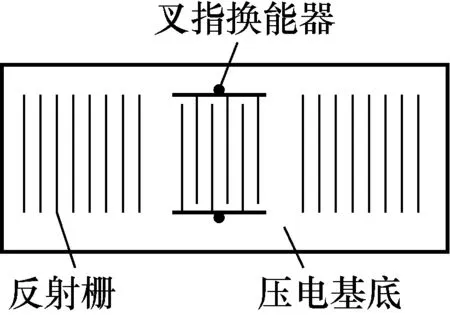
图1 声表面波谐振器Fig.1 Surface acoustic wave resonator
待测对象变化时,SAWR的谐振频率变化。对SAWR施加频率为f1的激励信号,回波响应信号为[9]:
(1)
式中:f0为待估计回波信号的载波频率,与SAWR的谐振频率fSAWR相等;A表示振幅;τ表示幅值衰减因子,与fSAWR及品质因数Q有关,τ=Q/fSAWR[10];φ表示初相位,为[0, 2 π ]范围内的随机变量。
3 算法原理
如式(1)所示的SAWR回波信号为幅度项、调制项、载波项的乘积。对幅度项中的指数衰减项进行抵消,并忽略调制项的影响,回波信号可简化为:
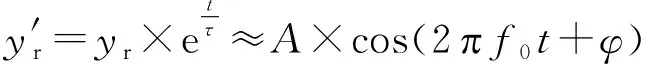
(2)
式中:T为回波信号的持续时间长度。
对回波信号进行离散化采样,可得:
ys(n)=A×cos(2 π f0Tn/N+φ)
(n=0, 1, 2,…,N)
(3)
式中N表示回波采样时间长度T内的采样点数。
对该离散化的回波信号进行FFT,结果为:
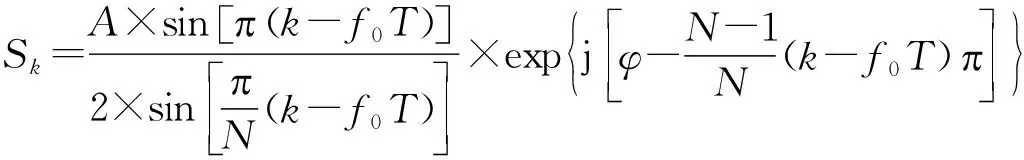
(4)
由式(4)可知,FFT的相位谱中包含了回波载波频率f0。但由于SAWR回波信号的初相位具有随机性,无法直接采用该方案估计回波频率。
对式(3)所示的回波信号进行自相关运算并化简,如式(5)所示:
cos[2 π f0T(n+m)/N+φ]
(5)
当信号采样点数N足够多时,式(5)中第二项的信号强度将趋近于零,可视作噪声信号。式(5)中第一项的信号初相位变为零。
忽略式(5)中噪声信号的影响,对其进行FFT,其相位谱中不再存在初相位。因此,可通过对回波信号自相关后的频域相位信息来估计回波频率。
4 算法验证
采用433 MHz频段的SAWR,通过SAWR无线测试系统对算法进行了验证。回波采样的时间长度T=16.384 μs,直接采用FFT的频率分辨率Δf=1/T=61 kHz,远不能满足实际应用要求,因此需要采用改进的频率估计算法。
改变激励信号的频率f1,回波频率估计结果如表1所示。从表1可知,本文算法的精度不受f1变化的影响,与现有Rife插值、抛物线插值算法相比,频率估计精度提高至少6倍,且稳定性也得到了显著增强。
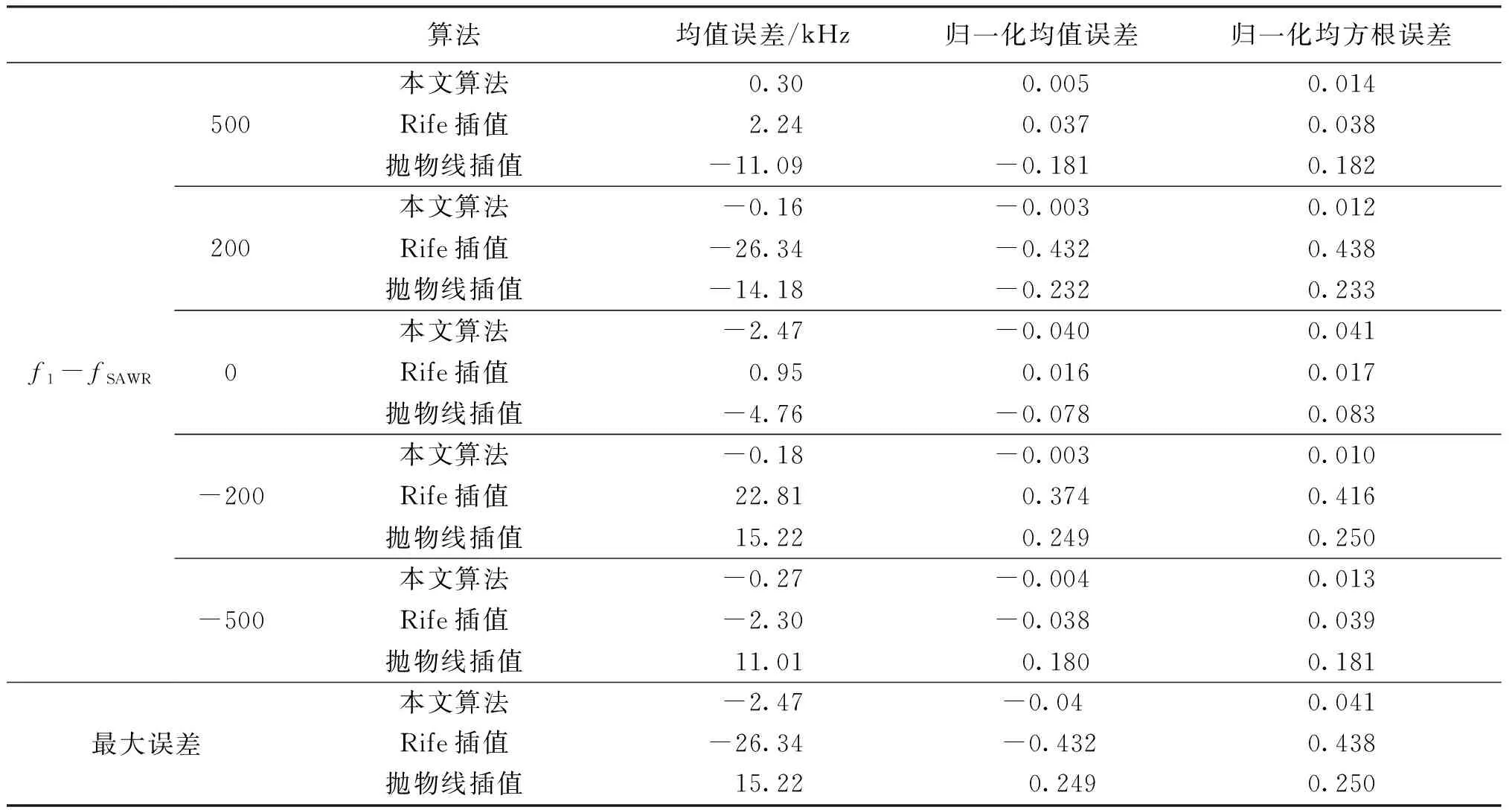
表1 回波频率估计结果随激励信号频率的变化Tab.1 Variation of echo frequency estimation results with excitation signal frequency
为分析fSAWR与FFT峰值谱线频率fM的偏差以及回波信号信噪比(Signal-to-noise ratio, SNR)对算法的影响,本文通过MATLAB构造如式(3)所示的SAWR采样回波信号,fSAWR的变化范围为[fM-Δf/2,fM+Δf/2],SNR采用函数awgn改变。图2为回波频率估计结果随fSAWR的变化。图3为回波频率估计结果随回波信号SNR的变化。
从图2(a)可以看出,本文算法在整个SAWR谐振频率变化范围内具有最佳的回波频率估计精度,远优于两种现有的估计算法。从图2(b)可知,本文算法在稳定性方面也远优于现有算法。由图3可知,无论SAWR谐振频率与FFT峰值谱线频率相等还是差异较大,本文算法的精度和稳定性均介于现有两种插值算法之间,且接近于最佳的算法,克服了Rife插值、抛物线插值算法在相应情况下频率估计误差大的缺点。

图2 回波频率估计结果随SAWR谐振频率的变化(SNR=0 dB)Fig.2 Variation of echo frequency estimation results with SAWR resonance frequency

图3 回波频率估计结果随回波信号信噪比的变化Fig.3 Variation of echo frequency estimation results with SNR of echo signal
5 结 论
本文针对现有SAWR回波频率估计算法存在的问题,提出了一种基于频域相位信息的频率估计新算法。与现有的Rife插值、抛物线插值算法相比,本算法具有以下优势:
(1)频率估计精度不受激励信号频率变化的影响。在激励信号频率与SAWR的谐振频率不相等时,仍可实现高精度的回波频率估计。
(2)在整个SAWR的谐振频率变化范围内都具有较高的频率估计精度和稳定性,不受SAWR谐振频率与FFT峰值谱线频率相对位置关系的影响。

