基于状态估计的海量多元异构智能电网数据压缩存储方法

马兴明， 董 成， 毛新宇， 焦玉新， 李 浩

(1.国网黑龙江省电力有限公司大庆供电公司，黑龙江 大庆 163311；2.武汉国电武仪电气股份有限公司，湖北 武汉 430074)

0 引 言

电力是经济发展的基础，我国对智能电网建设力度逐年加大。在智能电网的运行中，会出现海量多元异构智能电网数据[1-3]，其呈现出多样化的特点，会产生数据重复存储现象，导致智能电网系统资源利用率不高[4-6]。如何处理海量多元异构智能电网数据是智能电网公司亟待解决的难题[7]。

国内学者针对海量多元异构数据展开了众多研究，如闫会玉等[8]，研究工况数据压缩方法，根据从工业电气设备采集到的多维时间序列数据的变化情况设定死区限值大小，收集设备工况信息并标记工况标签，根据标签序列的变化制定设备运行状态分类规则，实现数据的分类压缩与存储。但是该方法在压缩时未能对海量多元异构数据进行数据处理，海量数据中的坏数据加大了计算难度，增加了压缩误差，影响了最终的压缩存储效果。王鹤等[9]研究基于分布式压缩感知的数据压缩存储方法，将设计的自适应联合重构算法应用到以分布式压缩感知为边缘算法的云边协同框架中，分析边缘上传的字典原子和测量值，实现电能质量数据的压缩存储。但是该方法在进行储存前没有对数据进行预处理，导致数据压缩存储过程中的冗余信息较多，增加了运行时间。

状态估计是智能电网基础数据处理方法，通过数据分析，预测智能电网设备质量状态，保证智能电网的正常运行。因此，本文提出基于状态估计的海量多元异构智能电网数据压缩存储方法，提高海量多元异构智能电网数据管理质量。

1 方法研究

1.1 基于状态估计的海量多元异构智能电网数据融合

多元异构数据是一种混合型数据，包括结构化数据和非结构化数据。在智能电网的运行中，数据来源较多，数据类型多种多样，且数据量较为庞大，数据融合的难度较大。因此，本文设计的数据压缩储存方法通过测量数据来识别海量多元异构智能电网数据[10]。状态估计是数据处理的重要方法之一，为提高智能电网数据的分析效率，将采集的海量多元异构智能电网数据进行实时数据处理，以此对数据状态进行估计，实现海量多元异构智能电网数据融合。

为了推导出准确的智能电网数据，依据状态估计的运算结果进行数据处理与参照物比较，识别海量多元异构智能电网数据。智能电网中状态估计数据与海量多元异构数据的融合流程如图1所示。

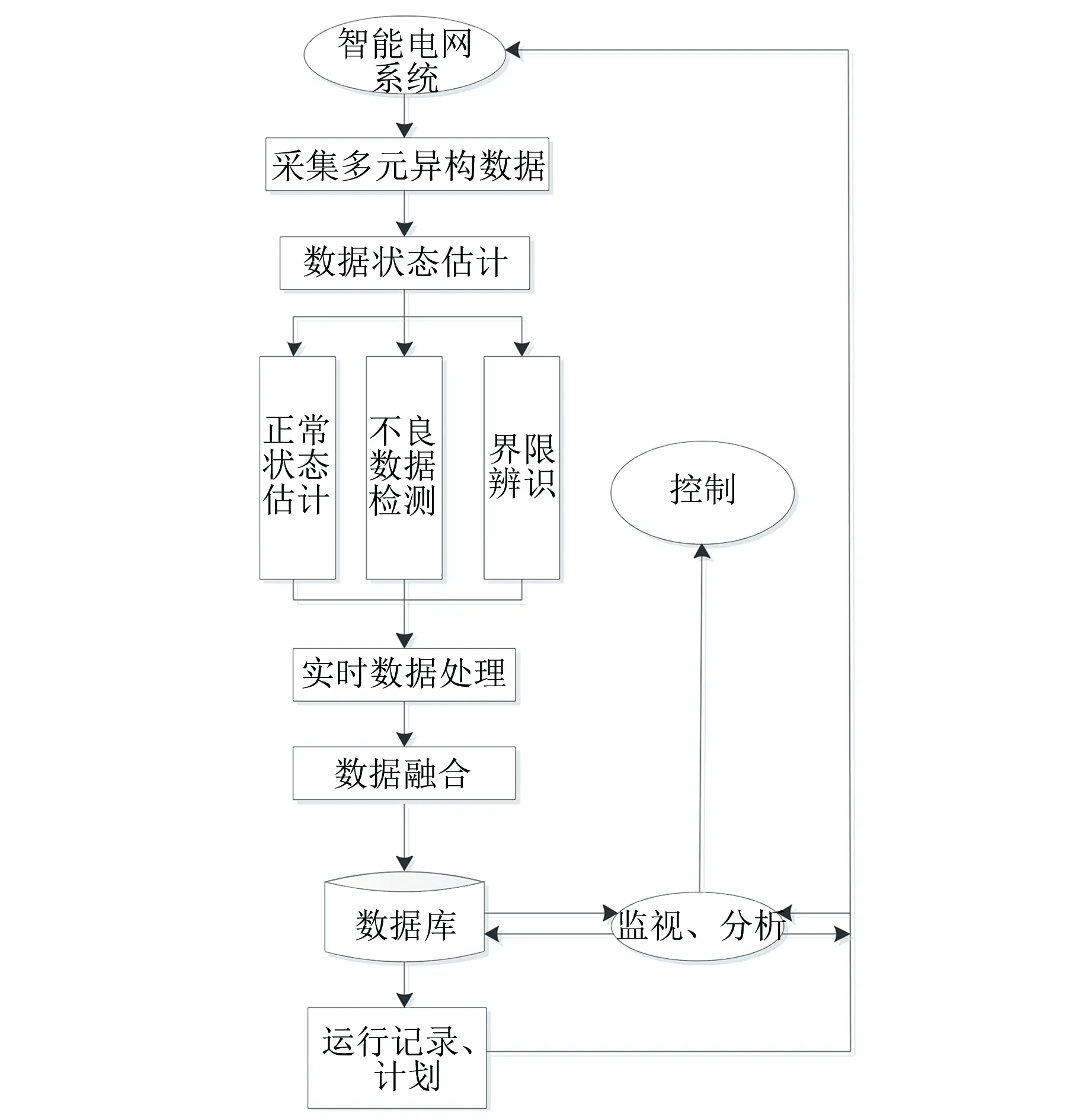
图1 状态估计数据与海量多元异构数据的融合流程

由图1可知，状态估计是智能电网数据处理的核心，利用状态估计实现正常状态估计、不良数据检测和界限辨识，将融合后的多元异构智能电网数据存入数据库[11]，为智能电网的监视、分析和控制提供数据支持。其中状态估计基于加权最小二乘法的状态估计方法实现，流程如图2所示。

图2 状态估计流程

海量多元异构智能电网数据内存在一些坏数据，若直接采用原始数据实施状态估计会降低准确性。为提升海量多元异构智能电网数据的状态估计质量，必须实施数据处理。坏数据处理包括四个环节，其中利用数态重获来查验智能电网的状态和数据来源，实施相关规则进行坏数据检测，采用决策树理论实施坏数据辨识与修补，经可观测性分析后完成坏数据处理。最后采用分解速度快的加权最小二乘法对处理后的数据实施状态估计。

1.2 基于张量Tucker分解的海量多元异构智能电网数据压缩方法

采用张量Tucker分解方法对数据融合后的海量多元异构智能电网数据实施压缩。首先分析海量多元异构智能电网数据，通过张量定义表明，BS∈EIN×It×Im表示数据张量的三个模展开矩阵，用下式描述：

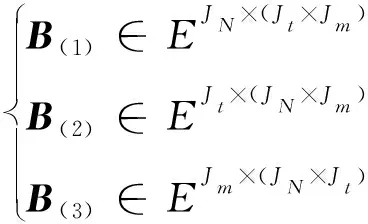
(1)

式中：B(1)为依据站点阶的模展开矩阵；JN为海量多元异构智能电网数据的站点；Jt为海量多元异构智能电网数据的采集时间；Jm为海量多元异构智能电网数据的量测量；B(2)为依据时间阶的模展开矩阵；B(3)为依据量测量阶的模展开矩阵。

通过变换方法分解张量的模展开矩阵，用下式描述：

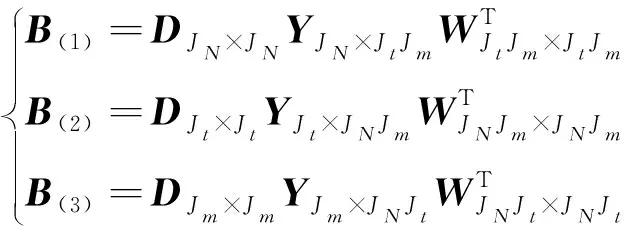
(2)

式中：D、W分别为左、右奇异值矩阵；Y为三个奇异值矩阵。

为获取三个模展开矩阵的近似奇异值分解公式，需选取奇异值τk之后的值，得到下式：

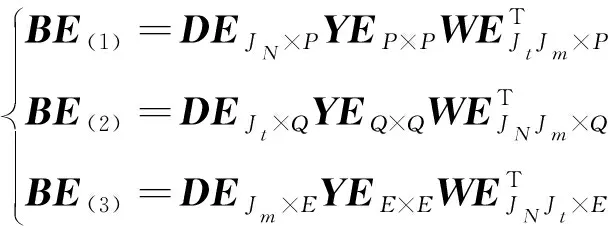
(3)

式中：DE、WE分别为选取的近似左、右奇异值矩阵；YE为第P、Q、E个奇异值中选取的近似奇异值对角阵；BE为奇异值分解近似阵。

通过Tucker分解处理n阶张量Bn，得到下式：

Bn=G×1D1×2D2×…×nDn

(4)

(5)

式中：G为压缩过程中的约束参数；D1、D2、…、Dn分别为对应阶的因子矩阵；H为核心张量。

依据式(5)对海量多元异构智能电网数据张量BY实施Tucker分解，得出压缩后的核心张量，如下所示：

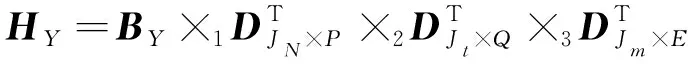
(6)

通过上式说明的正交基和原始张量，计算出核心张量HY∈EP×Q×E。所以原数据张量维度降到P、Q、E。

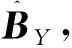
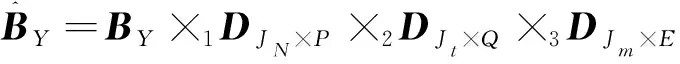
(7)

在海量多元异构智能电网数据中，非结构化的彩色图片、彩色视频和灰度视频数据[12,13]的张量模型阶数不同。

(1) 彩色图片数据。五阶核心张量用HP描述，其中HP∈EP3×Q3×…×D3；用BP表示彩色图片，计算出重构数据张量：

(8)

式中：Jc为图像颜色空间。

(2) 彩色视频数据。压缩后六阶核心张量用HCW描述，其中HCW∈EP2×Q2×…×D2；用BCW表示彩色视频，彩色视频的重构数据张量，用下式描述：

(9)

式中：Jf为图像帧。

(3) 灰度视频数据。压缩后五阶核心张量用HDCW描述，其中HDCW∈EP1×Q1×…×T1；用BDCW表示彩色视频，灰度视频的重构数据张量，用下式描述：

(10)

采用张量Tucker分解方法对数据融合后的海量多元异构智能电网数据实施压缩，流程如图3所示。

图3 张量Tucker分解的数据压缩流程

2 数据存储过程

在海量多元异构智能电网数据压缩后的存储过程中，通过采用可扩展标记语言(XML)技术实施数据预处理，将处理后的数据，利用非关系型的数据库(NoSQL)技术，实现海量多元异构智能电网数据的快速存储。

2.1 数据预处理

因压缩后的海量多元异构智能电网数据具有多样性，在进行数据储存之前，需采用XML技术标记数据、定义数据类型，对全部基础数据实施数据预处理，处理流程如图4所示。

图4 海量多元异构智能电网数据预处理流程

由图4可知，海量多元异构智能电网数据包括非结构化数据与结构化数据，针对不同的数据类型采用不同的数据处理流程，将数据以XML格式数据表存储至海量多元异构智能电网的各节点中，实现数据预处理。

2.2 数据快速存储优化策略

通过NoSQL，对预处理后的海量多元异构智能电网数据实施快速存储。实际数据在NoSQL上分配海量多元异构智能电网数据存储优化的存储策略如下。

(1) 按照内外网原则对海量多元异构智能电网数据主节点实施冗余计算。

(2) 分别储存智能电网的内外网海量多元异构数据，在对应单位的IT资源内存储智能电网的外网数据；智能电网内部IT资源只存储智能电网的内网数据。

(3) 按照不同对象分类存储智能电网外部海量多元异构数据；按照不同属性分类存储智能电网内部海量多元异构数据。

(4) 最小路径分配存储策略的出发点是NoSQL内的主节点，通过XML数据表调用元数据，依据元数据为原始数据配置相对容量的存储空间[14]，假如XML数据表内剩余存储空间较小,无法满足需求，依据相邻最近原则，通过续存方式分配所缺的原始数据存储空间[15]。

(5) 寻找空闲IT资源里智能电网节点路径，依据XML存储优先分配数据，实现快速存储。

3 试验分析

以某地智能电网25个配电站的真实监测数据集作为试验数据，其中包括结构化数据和非结构化数据，验证本文提出的基于状态估计的海量多元异构智能电网数据压缩存储方法的实际应用效果。

在智能电网稳定运行状态下，以某一条输电线路为例，随机选取6小时内的数据，并选取两种试验对比方法，分别为文献[8]面向电气设备的工况识别和数据压缩方法、文献[9]基于分布式压缩感知的配电网电能质量数据压缩存储方法。

3.1 不同方法估计线路电阻、电抗动态参数对比

由于海量多元异构智能电网数据来源较多，电网运行过程中的数据量较为庞大，某时段的电阻与电抗的数据是具有一定波动性的，因此计算电阻与电抗的动态参数能够进一步降低海量多元异构智能电网数据压缩误差。动态参数估计值与实际值越相近，说明该方法准确性越高，越能保证后期海量多元异构智能电网数据压缩效果。分析三种方法估计得到的线路电阻、电抗动态参数，结果如图5和图6所示。

图5 电阻动态参数估计

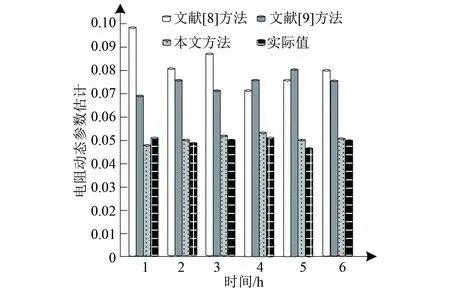
图6 电抗动态参数估计

由图5和图6可知，本文方法估计的线路电阻、电抗动态参数分别为0.032、0.530，结果明显优于其他两种方法，且与实际值非常接近，说明本文方法动态参数的估计准确性较高，能够保证后期海量多元异构智能电网数据的压缩效果。

3.2 不同方法对异常状态估计的结果精度对比

海量多元异构智能电网数据存在较多的变化。由于数据量较大，在数据压缩过程中服务器易出现过载情况。很多伺服驱动器的制动电阻因过载保护方法不当，会产生电阻突变，从而导致动态参数出现突然变化。因此，需要在进行数据压缩的过程中，对电网异常状态进行估计，准确预测动态参数变化趋势，对电网数据异常进行及时预警，实现智能电网数据的压缩存储。测试三种方法对异常状态下电阻动态参数的估计情况，其结果如图7所示。

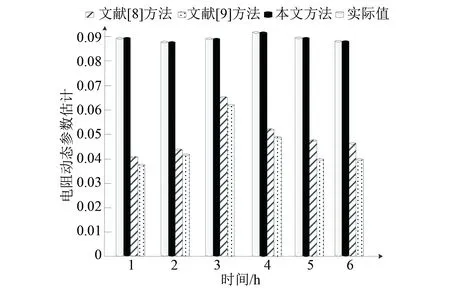
图7 异常状态下电阻动态参数估计

由图7可知，文献[8]方法与文献[9]方法并没有识别出异常状态下电阻动态参数的变化，与实际值差距较大，影响数据压缩效果。而本文方法采用张量Tucker分解对数据进行融合，估计的动态电阻与实际值基本一致，可识别出参数的异常变化，识别精度较高，能够实现异常状态下对参数突变的及时预警，实现智能电网数据的压缩存储。

3.3 不同方法的平均绝对误差和F-范数误差比

海量多元异构智能电网数据类型较多，因此在压缩过程中，很容易由于数据的复杂而增加压缩误差，影响压缩效果。因此计算三种方法的平均绝对误差(MAE)和F-范数误差比(FER)，二者越低，说明该方法的压缩误差越低，压缩效果越好。选取验证本文方法数据压缩效果的信息损失水平指标如下。

(1) 其第h个量测量的MAE如下：

(11)

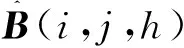
(2) 总体损失水平的FER如下所示：

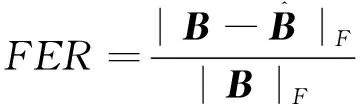
(12)

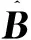
分析三种方法的压缩效果，结果如图8所示。

图8 数据压缩误差结果

由图8可知，本文方法所产生的压缩误差处于平稳并缓慢上升态势，尤其在低压缩比下，本文方法的误差明显低于其他两种方法。本文方法在不同数据压缩比下的压缩MAE、FER分别为0.240、0.025，均比其他两种方法的误差低，证明了本文方法的压缩误差低，压缩效果较好。

3.4 不同方法的运行时间对比

在并行计算模式下，测试三种方法的运行时间，结果如图9所示。由图9可知，本文方法的平均运行时间为213 ms，分别比其他两种方法的平均运行时间快353、257 ms，明显少于其他两种方法，说明本文方法的运行效率高，可实现海量多元异构智能电网数据的快速压缩存储。

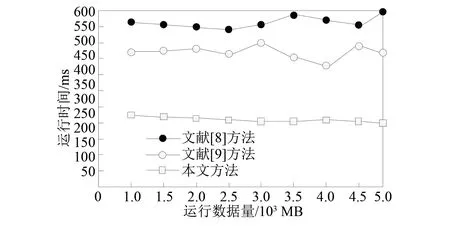
图9 不同方法运行时间

4 结 语

为了提高海量多元异构智能电网数据压缩存储效率，本文提出了基于状态估计的海量多元异构智能电网数据压缩存储方法。采用基于加权最小二乘法的状态估计实施数据融合，结合张量Tucker分解数据压缩方法和NoSQL技术实现海量多元异构智能电网数据的压缩存储。试验结果表明，本文方法的精度高，误差小，运行时间低至213 ms，运行效率高。