两种双边Halbach阵列永磁涡流制动特性对比研究

温建民， 罗 成

(1.中铁第四勘察设计院集团有限公司,湖北 武汉 430063；2.西南交通大学 电气工程学院,四川 成都 610031)

0 引 言

永磁涡流制动通过电磁感应原理，利用永磁体与导体间的相对运动，在导体中感生涡流，从而获得所需的制动力。其具有无接触磨耗、结构简单、噪声小、无断电失效、无线圈能耗等优点，目前已在轨道交通、升降装置等领域得到应用[1-3]。

对于永磁涡流制动技术已有相关研究。Jang等[4]和Sainjargal等[5]计算对比了水平磁化、垂向磁化、Halbach阵列三种单边永磁涡流制动系统的制动力，证明了Halbach阵列永磁涡流制动具有更好的制动能力。王江波等[6]、Jang等[7]和苑一祥等[8]利用麦克斯韦方程组建立磁场方程，结合磁场边界条件求得单边Halbach阵列永磁涡流制动系统磁场及制动力解析解。但单边磁场源除产生制动力外，还会产生影响系统稳定运行的法向力[9]。因此，肖尧等[10]通过有限元仿真对比了双边Halbach阵列及常规双边永磁涡流制动性能，发现双边Halbach阵列永磁涡流制动在高速时具有更好的制动性能。Chen等[11]通过计算发现双边Halbach阵列竖向磁化方向相同时，产生的涡流制动力在100 km/h的速度范围内比阵列竖向磁化方向相反时大得多。但其解析计算公式未考虑阵列磁场边端效应及气隙谐波的影响，计算结果误差较大。而陈殷[12]则利用解析法重点研究了双边Halbach阵列竖向磁化方向相反时的永磁涡流制动在高速磁浮中的制动性能。但其制动力在低速时远小于双边Halbach阵列竖向磁化方向相同时的涡流制动力。

基于以上研究，本文对两种双边Halbach阵列永磁涡流制动系统方案进行研究。首先建立系统解析模型，推导出系统涡流制动力。然后搭建有限元模型，对制动力解析结果进行验证，并利用制动力解析式对比了两种系统方案的制动能力。最后分析系统参数对方案1制动性能的影响。

1 解析计算

两种双边Halbach阵列永磁涡流制动示意图如图1所示。图中，l、h分别为永磁体长度与高度，l1、l2分别为Halbach阵列及导体板长度。

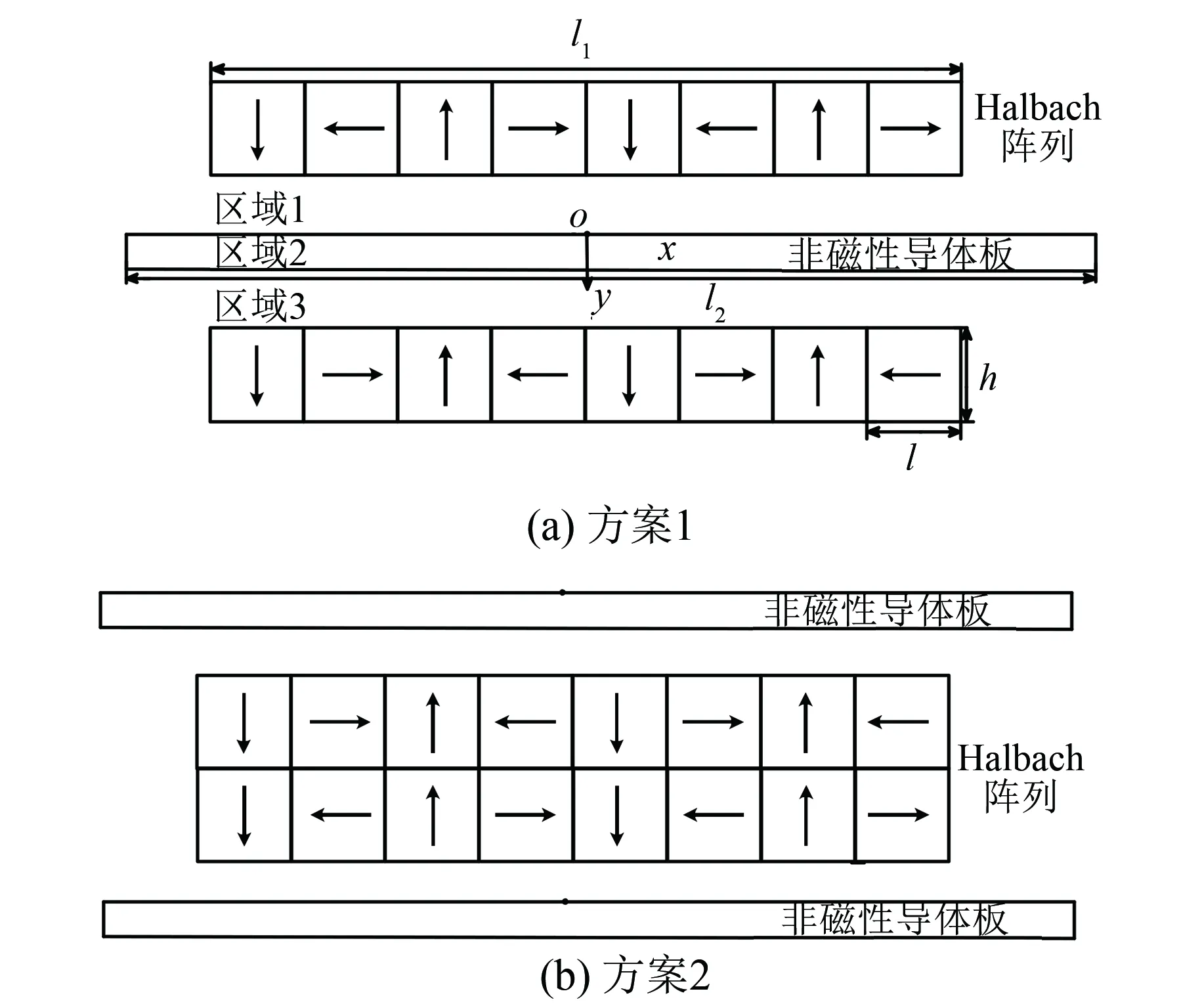
图1 两种双边Halbach阵列永磁涡流制动示意图

1.1 方案1制动力计算

如图1(a)所示，首先求解双边Halbach阵列在空间中产生的源磁场。根据文献[13]，利用面电流法，将单块永磁体产生的磁场等效为两侧面电流在空间中产生的磁场叠加，进而求得双边Halbach阵列产生的源磁场。求解的双边Halbach阵列源磁场已考虑气隙谐波及端部效应，故对其进行傅里叶分解[14]：

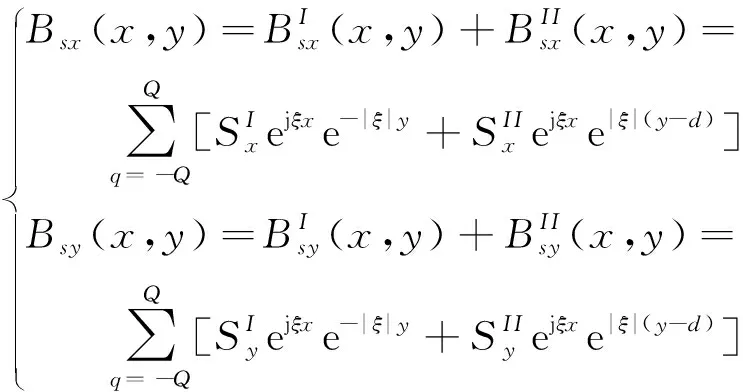
(1)

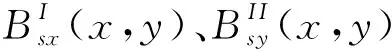
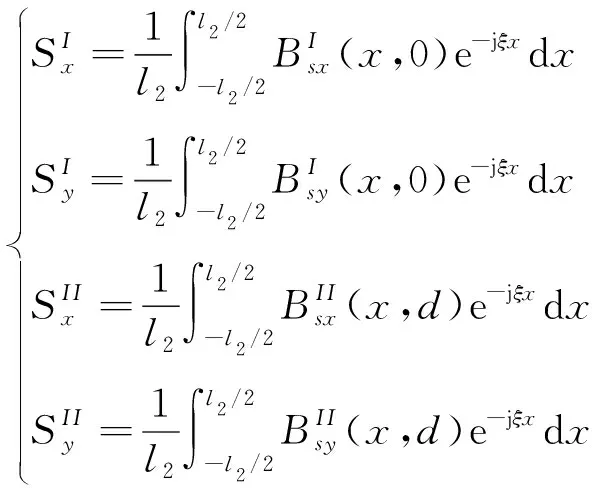
(2)

当双边Halbach阵列与导体板间以速度vx相对运动时，利用麦克斯韦方程组可得矢量磁位A方程为[15]

(3)

式中：ki为传播函数；Js为导体板中的感生涡流，且：

大洋钻探的另一大挑战是钻头必须在操作中期更换。海洋的地壳由火成岩组成，这些岩石在钻头达到预期深度之前就会将其磨损。出现这种情况时，钻工将整个钻杆拉出，安装好新钻头后再插入同一个钻孔。这需要引导钻杆进入漏斗状的再入锥。再入锥的宽度不到15英尺，放置在海底的钻孔口。这一过程在1970年首次完成，它就像把一根长长的意大利面放入奥运会游泳池底部宽0.25英寸的漏斗中一样。确认板块构造

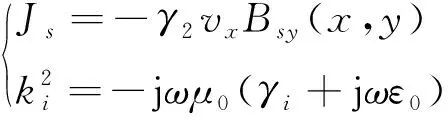
(4)

式中：γ2为导体板电导率；ω为角频率(ω=-ξv)；γi分别为气隙 (i=1,3)和导体板(i=2)的电导率；μ0、ε0分别为真空磁导率及真空介电常数。

由于在二维模型中感应涡流仅包含z方向分量。故根据式(4)的矢量方程得到各区域标量方程为

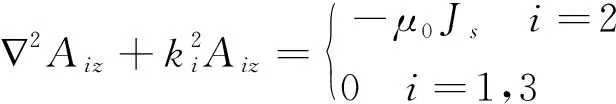
(5)

根据文献[14]，矢量磁位方程(5)的通解可利用分离变量法及磁场边界条件求得。将求得的感生涡流磁场与双边Halbach源磁场求和，可得系统磁场为

(6)

根据麦克斯韦张量法，可求得制动力解析式为[16-18]

(7)

式中：w2为导体板横向宽度。

1.2 方案2制动力计算

如图1(b)所示，方案2为中间双边Halbach阵列与两侧导体板间做相对切割运动，在两侧导体板感生涡流产生所需的制动力。为简化运算，忽略背靠背Halbach阵列磁场的相互耦合，将其等效为两个单边永磁涡流制动。因此，根据麦克斯韦张量法可求得方案2制动力解析式为[16-18]

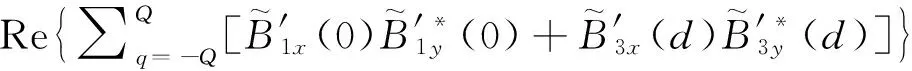
(8)

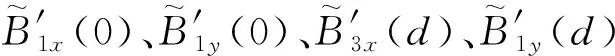
2 有限元验证

根据表1所示的有限元模型参数，利用Ansys Maxwell软件分别搭建方案1、方案2双边Halbach阵列永磁涡流制动有限元模型，并对推导的制动力解析解进行验证，得到两种方案的磁感应强度如图2所示。

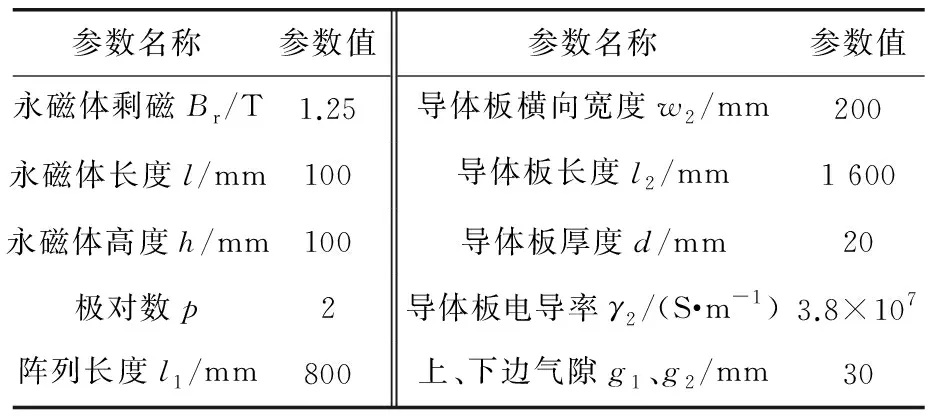
表1 模型参数

从图2(b)可以看出，方案2中背靠背Halbach阵列磁场存在明显的相互耦合。

不同速度下，制动力解析模型与有限元模型计算结果对比如图3所示。由图3可见，方案1制动力解析解与有限元计算结果十分吻合，其计算平均相对误差仅为0.87%。而由于解析计算忽略了背靠背Halbach阵列磁场耦合效应，方案2解析计算结果比有限元计算结果大，二者平均相对误差为7.21%。且方案1为上、下阵列磁场叠加，方案2为两个单边Halbach永磁涡流制动力的叠加，故低速段方案1制动力接近方案2制动力的2倍，而随着速度的提高，由于集肤效应，二者制动力趋于相近。

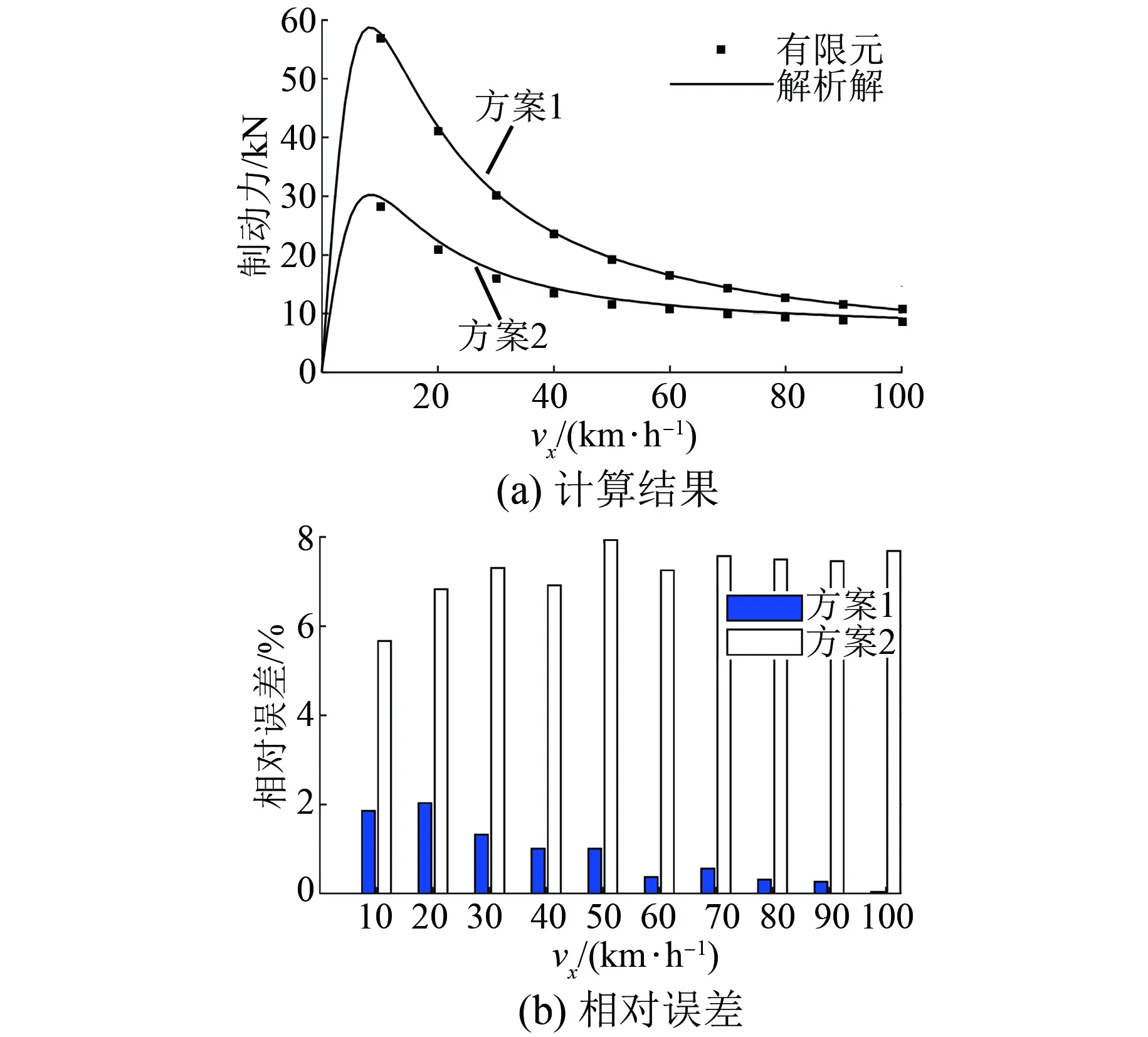
图3 制动力解析模型与有限元模型计算结果对比

3 参数分析

影响永磁涡流制动性能的参数主要有永磁体尺寸、气隙、导体板电导率及厚度。考虑到永磁体尺寸的变化会影响其体积和质量，因此除了考虑其对制动力的影响外，本文还选取最大制动力与永磁阵列体积比作为分析目标。在分析气隙及导体板参数对制动性能的影响时，由于永磁阵列参数不变，仅分析其对制动力的影响。由第2节分析可知，方案1的制动能力在低速段明显优于方案2，故本节仅分析方案1参数对其制动力的影响。除了分析参数的变化外，其他参数如表1所示。

3.1 永磁体长度及高度

永磁体长度和高度变化对制动力的影响分别如图4、图5所示。由图4、图5可见，制动力随着永磁体长度或高度的增加而增大，但增大幅度在逐渐减小。且永磁体长度或高度的变化不影响取得最大制动力时的速度(v=8 km/h)。选取最大制动力Fxmax与双边Halbach阵列体积Vm之比，分析其随永磁体长度和高度的变化曲线，如图6、图7所示。

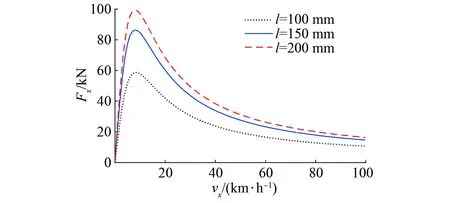
图4 永磁体长度变化对制动力的影响

图5 永磁体高度变化对制动力的影响

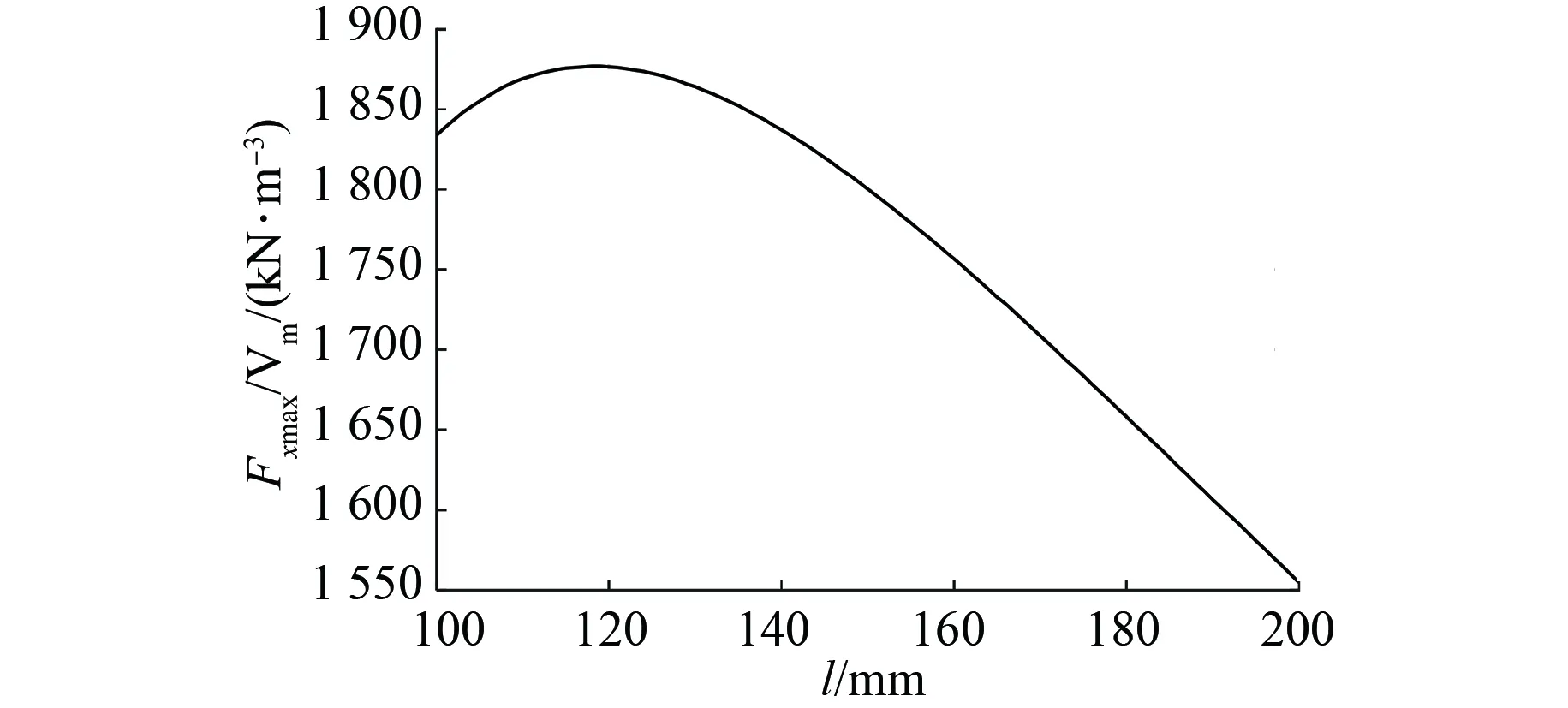
图6 Fxmax/Vm随永磁体长度的变化曲线(h=100 mm)

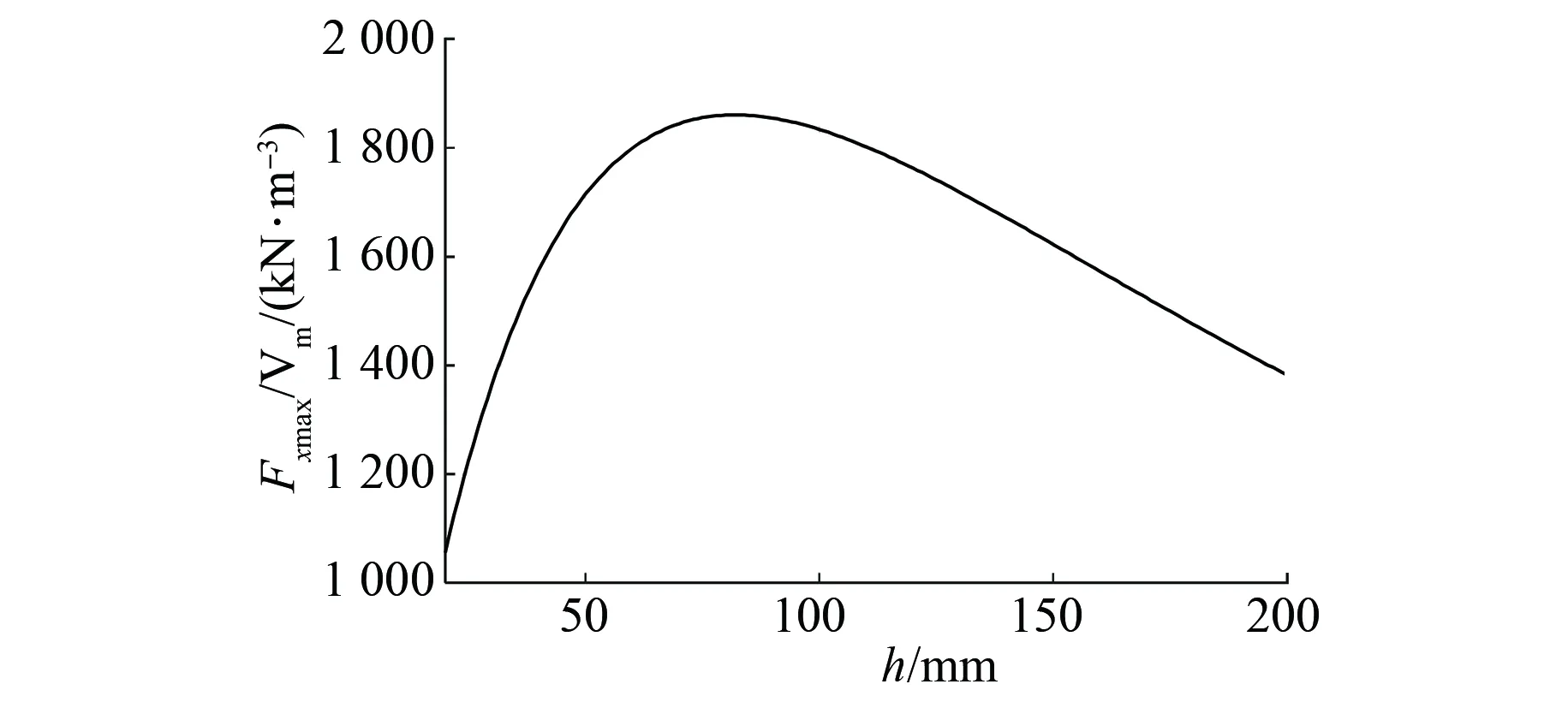
图7 Fxmax/Vm随永磁体高度的变化曲线(l=100 mm)

由图6、图7可见，随着永磁长度或高度的增大，Fxmax/Vm先增后减，其基本在永磁体长度与高度比l/h=1.2时取得最大值。因此，为取得最大制动效率，永磁体长高比应取1.2。

3.2 气隙

制动力及法向力随气隙变化的曲线如图8所示。其中，系统法向力Fy可根据麦克斯韦张量法求得[16-18]。

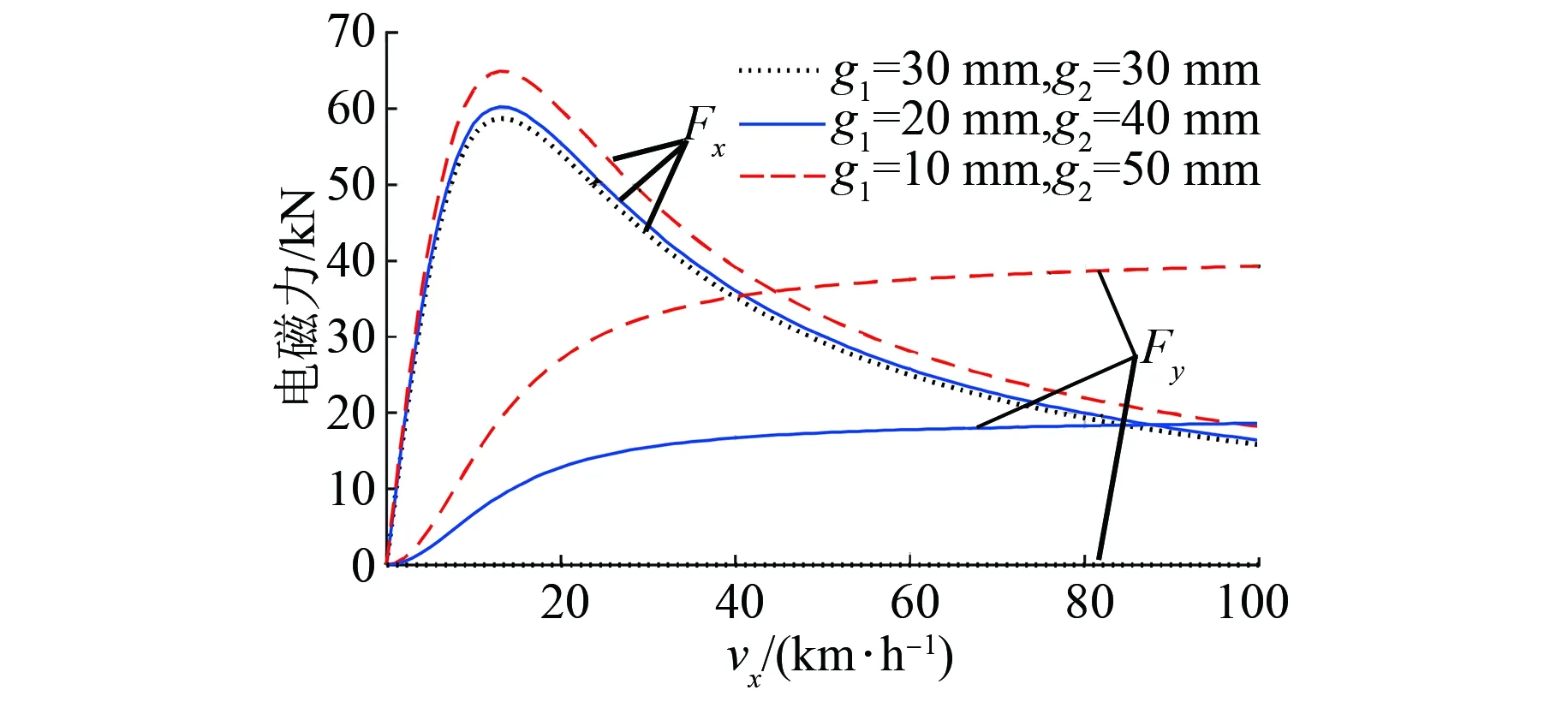
图8 气隙变化对制动力的影响

由图8可见，单边气隙的减小，可适当增大制动力，但法向力也随之迅速增大。法向力的产生会影响系统的稳定运行，因此上、下部气隙应相等。

3.3 导体板电导率及厚度

导体板电导率和厚度变化对制动力的影响如图9、图10所示。

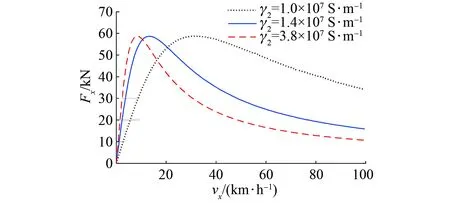
图9 导体板电导率变化对制动力的影响

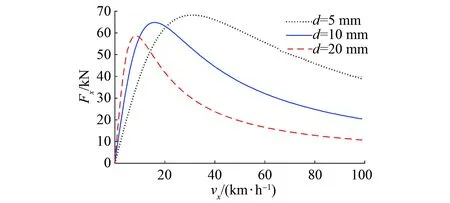
图10 导体板厚度变化对制动力的影响

由图9、图10可见，导体板电导率的变化不影响最大制动力，但会改变最大制动力的速度。电导率越大，最大制动力对应的速度就越小。导体板厚度的减小会增大制动力及其对应的速度。

4 结 语

本文推导了两种双边Halbach阵列永磁涡流制动方案制动力的解析解。对比分析了两种制动方案的制动力，得到低速段时方案1制动力接近方案2制动力的2倍。分析了永磁体尺寸、气隙、导体板参数对方案1制动性能的影响，得到以下结论。

(1) 制动力随着永磁体长度或高度的增加而增大，但增大幅度逐渐减小，且永磁体尺寸的变化不影响取得最大制动力时的速度。为取得最大制动效率，永磁体长高比应取1.2。

(2) 气隙的减小可适当增大制动力，但法向力也随之迅速增大。法向力的产生会影响系统的稳定运行，因此上、下部气隙应相等。

(3) 导体板电导率增大，最大制动力不变，但其对应的速度减小。导体板厚度的减小会增大制动力及其对应的速度。

(4) 本文研究的两种双边Halbach阵列永磁涡流制动，克服了单边永磁涡流制动法向力，提升了制动性能，对需要大制动力及稳定运行要求高的轨道交通和机械装置，具有较高的实用价值。