基于负序故障附加网络模型识别的有源配电网保护*

韩 笑， 丁煜飞， 夏寅宇， 汪缪凡， 齐沛锋

(南京工程学院 电力工程学院,江苏 南京 211167)

0 引 言

“碳达峰、碳中和”目标提出后，我国电网呈现出高比例清洁能源与高比例电力电子器件的“双高”态势。以太阳能与风能为代表的清洁能源分布式发电得到了快速的发展与推广，并可以预见，未来配电网将采用分布式电源高度渗透的有源配电网[1-2]。因此研究适用于新型配电网的继电保护原理与解决方案，对提高新型配电网故障切除速度、保证供电可靠性有重要意义。

基于单端量的传统电流保护很难适应有源配电网的故障特征，容易出现保护误动、拒动问题[3-8]。为解决有源配电网保护存在的难题，针对有源配电网的新故障特征，以多端信息量构成的纵联保护逐渐成为主流[9-11]。但配电网网络拓扑多样，存在不可测负荷分支的影响，对纵联差动保护的整定造成了很大困扰[12-14]。利用幅值比信息、电流相似性比较等方案能提高保护含不可测负荷分支线路的可靠性。上述方案均基于正常运行下潮流方向不发生改变的情况来设计保护判据，但有源配电网运行方式多样，存在分布式电源向上级线路输送潮流的运行状态，这对保护的识别能力又提出了新的要求。

因此，针对目前研究的不足，本文讨论了含分布式电源与不可测负荷分支的配电网故障特征，基于不同故障下被保护线路模型之间的不同，提出了一种基于模型识别的保护原理，利用负序故障附加网络中被保护线路是否判断为有源来设计保护判据，并在含有不可测负荷分支的工况下进行理论分析与仿真验证，最后通过PSCAD仿真软件，验证了本文所提方案在含不可测负荷分支线路中的可行性。

1 含不可测负荷分支线路的故障分析

1.1 区内不对称故障时的模型特征

含分布式电源的配电网拓扑如图1所示。

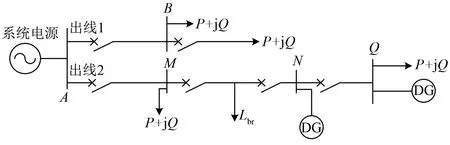
图1 含分布式电源的配电网拓扑

图1中，Lbr为不可测负荷分支，DG为分布式电源。分布式电源的故障模型一般采用正序受控电压源，因此可以在故障后的负序网络中等效为开路。取线路中MN段进行故障分析，对负荷采用恒阻抗模型进行等效，MN段线路对应的负序附加网络图如图2所示。

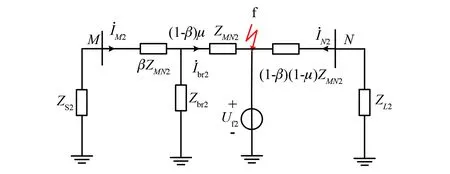
图2 区内故障MN线路负序附加网络图

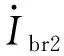
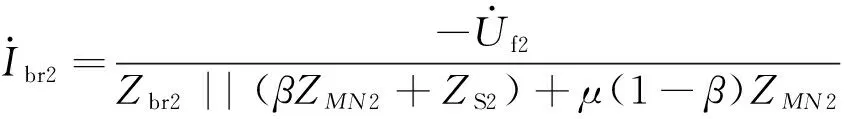
(1)

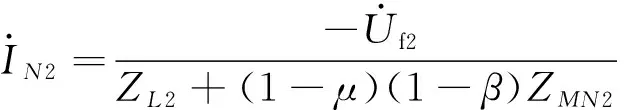
(2)

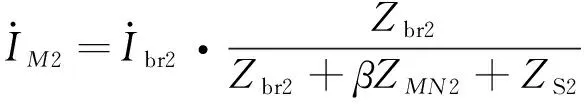
(3)

由于Zbr2远大于ZMN2，且故障时负荷分支流过的电流可以忽略不计，故可以认为Zbr2=∞，可以将式(3)进行化简得：

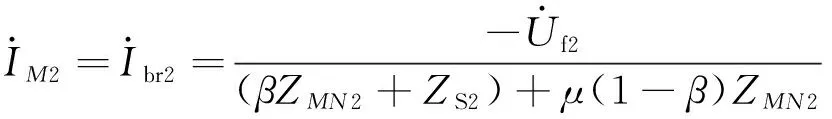
(4)

由两侧保护安装处的负序电流可以推出两侧保护安装处的负序电压为

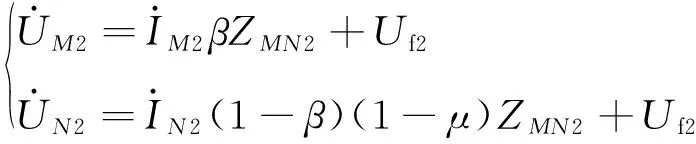
(5)

1.2 区外不对称故障时的模型特征

被保护线路的区外故障包含上游故障与下游故障两类，本文以线路MN下游发生不对称故障为例进行分析，系统的负序故障附加网络图如图3所示。

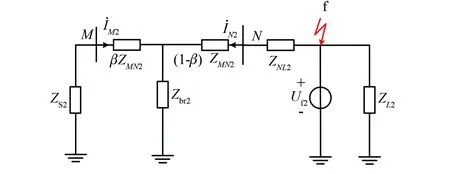
图3 区外故障MN线路负序附加网络图

图3中，故障点下游线路与负载阻抗合并，统称为ZL2，ZNL2为N侧母线到故障点多额等值阻抗，其他阻抗定义与区内故障分析时一致，此时流过两侧保护安装处的电流为

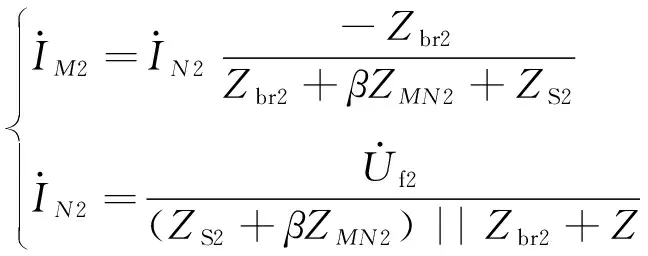
(6)

式中:Z=(1-β)ZMN2+ZNL2。

由于Zbr2远大于ZMN2, 且故障时负荷分支流过的电流可以忽略不计，故可以认为Zbr2=∞，可以将式(6)进行化简得：

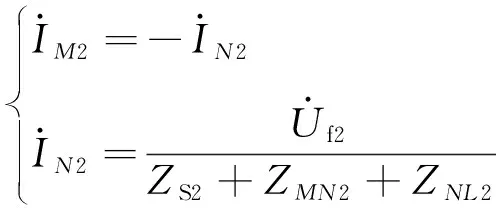
(7)

由两侧保护安装处的负序电流可以推出两侧保护安装处的负序电压为

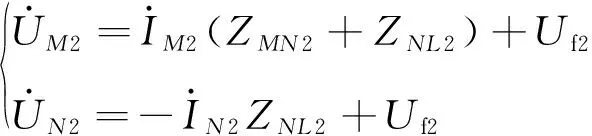
(8)

2 保护判据设计

2.1 方案原理

由上文故障分析可知，当区内发生故障时，线路MN的等值模型中包含等值电压源Uf2，而区外发生故障时，MN等值模型中不包含等值电压源Uf2。通过瞬时对称分量法，可将瞬时故障电压分量和瞬时故障电流分量分解为正序、负序和零序分量，得到负序故障分量瞬时功率表达式为

p2=ua2ia2+ub2ib2+uc2ic2=

3U2I2cos(φu2-φi2)

(9)

式中：U2、I2为负序分量有效值；φu2、φi2分别为负序电压、电流的相角。

对于同一故障，故障分量负序功率的瞬时值是一个具有单极性特点的恒定值，故通过对其极性的分析可以判断故障的区段。对于区内故障，由于在负序故障附加网络中有等值电压源Uf2的存在，其在一个数据窗内吸收的能量W(t0,t)为负值，对于区外故障，线路等值网络中不包含虚拟电压源Uf2，其在一个数据窗内吸收的能量W(t0,t)为正值。借助此差别，可以构建模型识别保护判据为W(t0,t)<0。为保证判别的可靠性，数据窗的长度应为一个完整的工频周波，即20 ms。

2.2 保护判据验证

将上文分析得到的负序电流与负序电压代入式(9)进行分析。当发生区内故障时，线路M侧的负序电压与电流夹角为

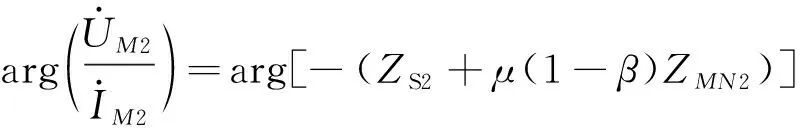
(10)

当发生区内故障时，负序故障分量瞬时功率小于0恒成立。通过对一定时间窗内负序故障分量瞬时功率的积分得到的W(t0,t)<0，可以判别为区内存在等值电压源，进而判别为保护区内部存在故障。

当发生区外故障时,以上文分析的下游区外故障为例，线路M侧的负序电压与电流夹角为

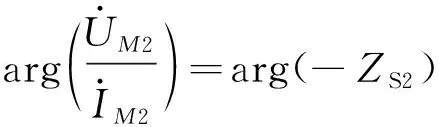
(11)

综上分析，线路负序附加模型的区外故障与区内故障可以分别被证明为无源网络与有源网络，验证了本文所提方案的可行性。

2.3 保护流程

针对有源配电网的模型识别，可以根据被保护对象负序故障网络两侧电压、电流的相关性，构造基于模型识别的保护判据，有效解决保护误动、拒动问题。保护的整体流程图如图4所示，整体流程步骤如下：

(1) 当保护启动装置检测到发生不对称故障时，保护启动，采集线路两侧一个周波的电压、电流数据，通过终端装置上传到主站；

(2) 根据采集到一个周波的两侧电气量计算负序电压与负序电流有效值与相角；

(3) 将计算得到负序电压、电流有效值与相角代入W(t0,t)表达式，并计算W(t0,t)；

(4) 若满足W(t0,t)<0则保护动作，否则返回步骤(1)。

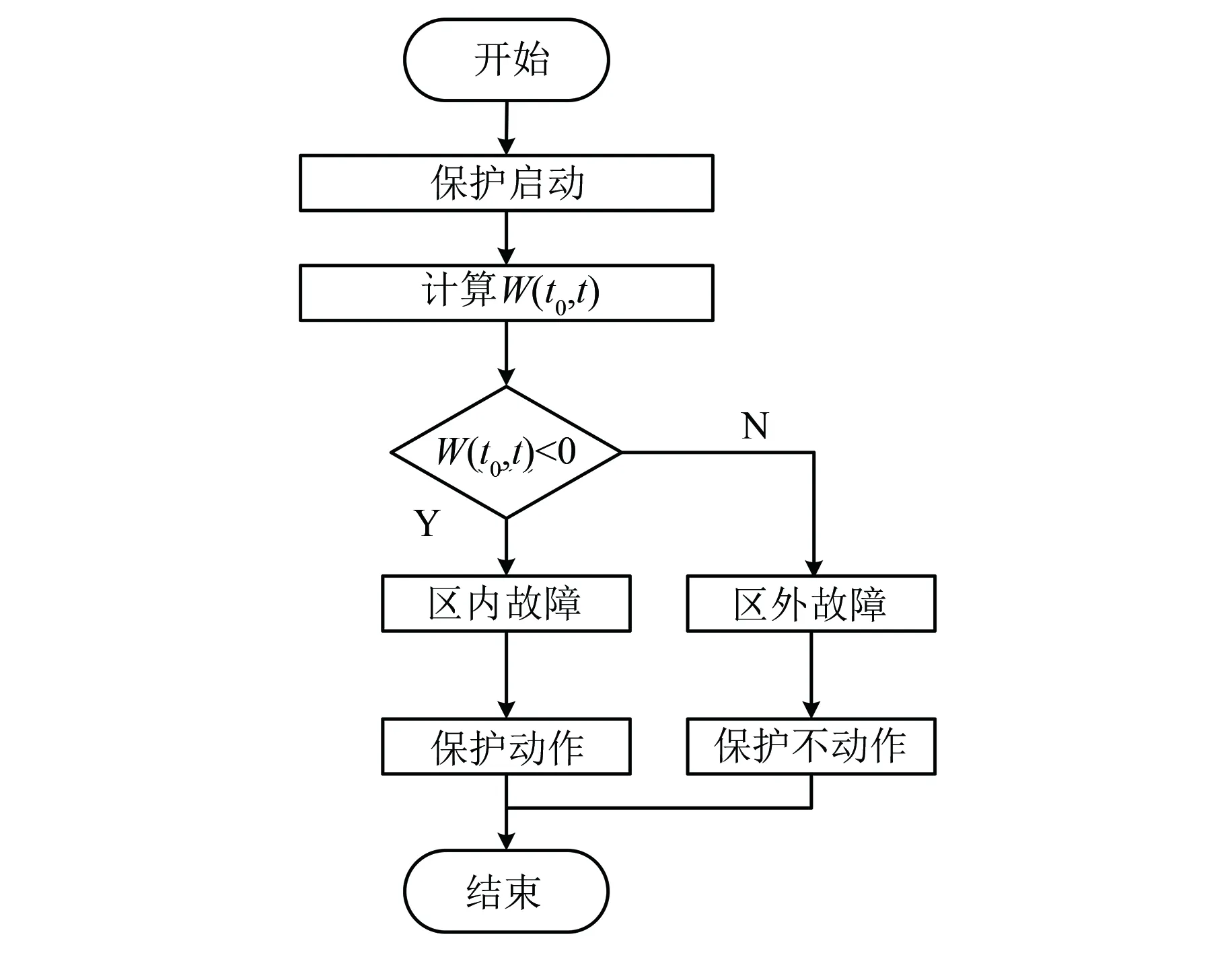
图4 保护方案流程图

3 算例分析

为了验证基于线路负序模型识别的保护原理对有源配电网故障保护的有效性，在PSCAD仿真软件中搭建了如图1所示的仿真模型，被保护对象为线路MN，线路AB、AM、MN、NQ的长度分别为5、3、4、2 km，单位线路长度参数为Z=0.12+j0.43 Ω/km。分布式电源容量为1.5 MVA，接入母线N侧，设置出线1线路末端负荷为3 MVA，出线2线路末端负荷为3 MVA，负荷功率因数均为0.85。

3.1 区内故障下保护动作情况

假设线路MN的75%处发生故障，不可测负荷分支接于线路50%处，通过改变故障类型、不可测负荷分支容量占下游总负荷的比值、不同的故障过渡电阻Rg，对保护的有效性进行验证。考虑到故障后逆变器需要进行低电压穿越，维持并网点电压稳定，短时间内产生大量杂乱的谐波，需要一定的控制调整时间，故仿真取保护检测到故障10 ms后的电气量进行故障判别。故障类型设置的过渡电阻值与对应的W(t0,t)与保护动作结果如表1与表2所示。

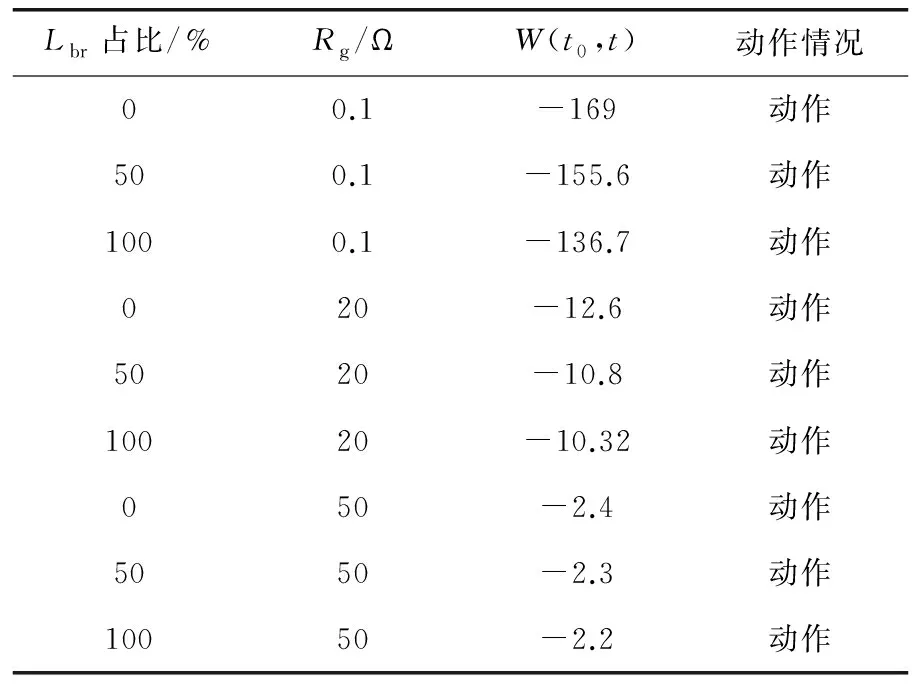
表1 区内单相接地故障仿真结果与动作情况

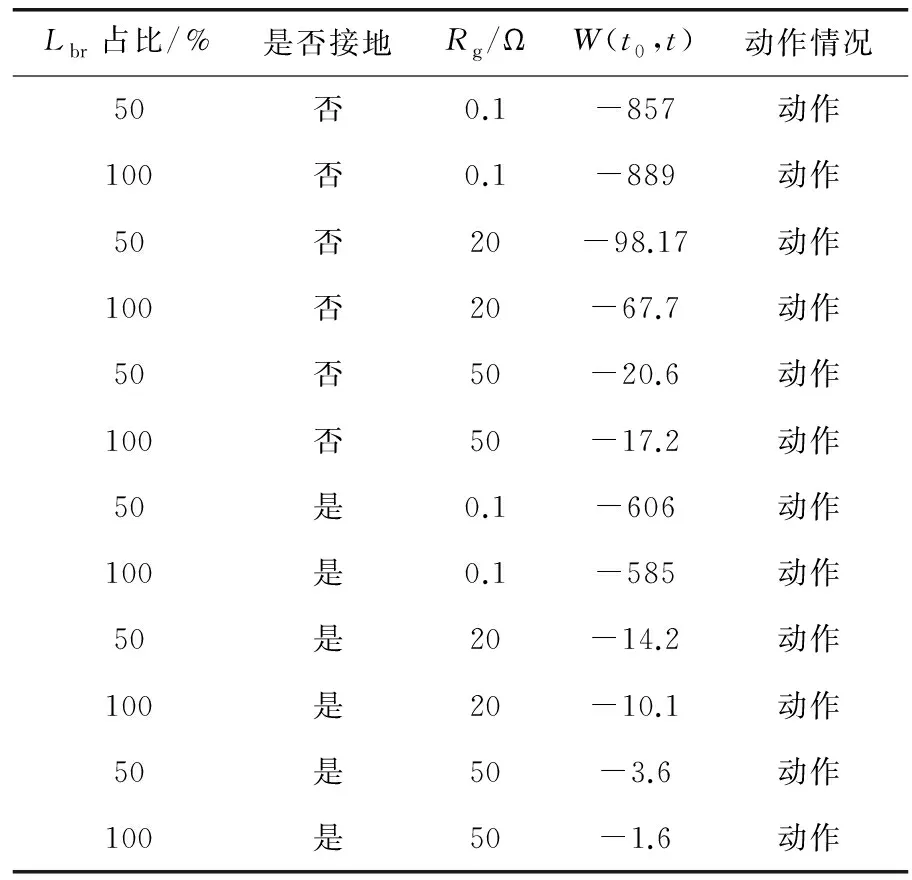
表2 区内两相短路故障仿真结果与动作情况

由表1与表2可知，在不考虑过渡电阻的情况下，当发生区内故障时，保护方案能准确判别故障位置，并存在一定区分度。过渡电阻增大时，故障电流减小，导致W(t0,t)数值下降，在考虑到50 Ω的过渡电阻时，保护判据依然有一定区分度。因此对于含不可测负荷分支的区内故障，本文所提保护方案有较强的抗过渡电阻能力与保护灵敏性。

3.2 区外故障下保护动作情况

区外故障包含分布式电源接入点上游故障与下游故障。假定故障点均位于对应线路中点处，当发生区外故障时，各种故障类型下的区外故障与对应保护动作情况如表3与表4所示。

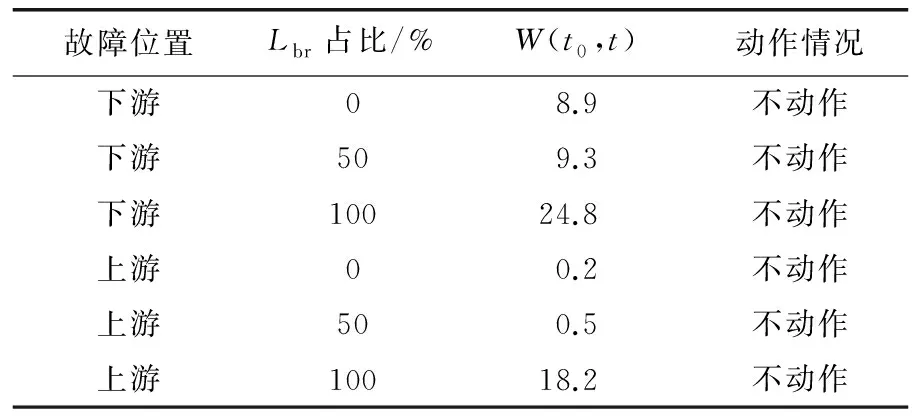
表3 区外单相接地故障仿真结果与动作情况

表4 区外两相短路仿真结果与动作情况

由表3与表4可知，当分布式电源接入点下游线路或上游线路发生故障时，计算得到的W(t0,t)均大于0，保护不动作。

3.3 下游负荷占比较小时保护动作情况

分布式电源大多具有间歇性、随机性的特点。比如光伏电源，当日照充足时，光伏电源输出功率大，当下游负荷容量小于光伏电源出力时，光伏电源就会向上游线路输出反向潮流；而日照不充足时，光伏电源出力小，光伏电源仅向下游输出功率。即在一天的运行周期中分布式电源可能存在向上游输出潮流的情况，而现有的不可测负荷分支检测方案大都建立在潮流方向确定的网络中。这些方案不能正确反应故障方向，使其保护判据不再适用。

而本文所提方案不受有源配电网运行方式的影响，在下游负荷突然减小、分布式电源向上游输出潮流的情况下，其负荷变化在负序网络中没有体现，所以保护不会误动。

4 结 语

分布式电源的接入使传统配电网演变成了有源配电网，容易造成继电保护的误动作。而不可测负荷分支的接入也导致保护配置与配合出现难题。本文提出一种针对含不可测负荷分支线路的配电网模型识别保护方案，通过计算负序网络在一定时间窗内的功率积分来分辨故障位置。经过理论分析与仿真分析，验证了本文所提保护方案在多种运行方式与不对称故障工况下的可靠性。