一类非交换群环的单位群和零因子*

黄逸飞 郭述锋*

(桂林航天工业学院 理学院，广西 桂林 541004)

群环是一个重要的环类，它不仅与群论、环论有关，而且与域论、线性代数、代数数论、代数拓扑等理论有紧密的联系。近年来，群环在密码、通信等领域都有着广泛的应用。研究群环的代数性质和结构一直是群环研究中的一个重要课题，因为这对于群环的应用是非常重要的。整群环的单位群在研究群环代数性质方面非常广泛，比如文献[1-3]等，但是对群代数FG的单位群的结构刻画的较少。M.KHAN和R.K.SHARMA等分别在文献[4-5]中研究了FS4和FA4的单位群结构。本文对FDm的代数结构、单位群和零因子给出来了一个较为具体的刻画。

1 基本概念与记号

记FG为群G在域F上的群代数，若群H是群G的一个正规子群，则从G到G/H的自然同态可以扩张到FG到F[G/H]的代数同态，定义作∑g∈Gagg∑g∈GaggH，记这个同态的核为△(G,H)，△(G,H)是FG中由{h-1|h∈H}生成的一个理想，显然有FG/△(G,H)≅F[G/H]。△(G)是群代数FG的增广理想，那么FG/△G≅F，意味着群代数FG的Jacobson根J(FG)包含在△(G)中.对任意理想，若I⊆J(FG)，从FG到FG/I的自然同态可诱导一个从群代数FG的单位群u(FG)到u(FG/I)的同态满射，并且核为1+I，显然我们可以得到u(FG)/1+I≅u(FG/I)。

设R为一个有单位元的环，D(R)表示环R的零因子集合，|D(R)|为环R的零因子个数。M(n,F)表示在域F上的n阶全矩阵，GL(n,F)表示域F上的n阶一般线性群，charF是域F的特征，而F*表示域F中非零元构成的乘法群，F2是F的二次扩域。

2 若干引理

为证明本文主要结果，下面给出若干必要的引理：

引理1(文献[7]命题3.6.11)设K是一个特征为p的域，p>0，G是一个含有正规p-子群P的有限群，若p†|G/P|，则J(KG)=△(G,P)。

引理3(文献[7]命题3.3.3)集合BH={q(h-1):q∈T,h∈H,h≠1}是△(G,H)在R上的基，其中T是H在G中的陪集代表系。

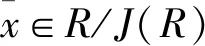
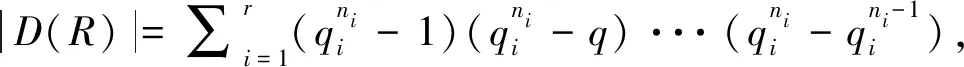
其中：qi是素数的方幂，n1，…，nr，r为自然数。

3 主要结果

定理1设FS3为三次对称群S3在有限域F上的群代数，J(FS3)为FS3的Jacobson根，则：

1)若|F|=2n，则FS3/J(FS3)≅M(2,F)⊕F，

2)若|F|=3n，则FS3/J(FS3)≅F⊕F，其中J(FS3)=△(D5,H)，H={1,a,a2}，

3)若|F|=pn，charF=P>3，则FS3≅M(2,F)⊕F⊕F。

证明：1)若|F|=2n，则dimFJ(FS3)=1，那么dimFFS3/J(FS3)=5，又因为FS3/J(FS3)是非交换的，所以FS3/J(FS3)≅M(2,F)⊕F。

2)易验证H◁S3，且|S3/H|=2，那么charF†|S3/H|，根据引理1知：J(FS3)=△(G,H)。又根据引理3知：{a-1,a2-1,b(a-1),b(a2-1)}为△(S3,H)在F上的一组基，所以△(S3,H)在F上的维数为4，即dimFJ(FS3)=4，那么dimFFS3/J(FS3)=2，从而FS3/J(FS3)只可能同构于以下两种形式：

FS3/J(FS3)≅F⊕F，FS3/J(FS3)≅F2，

又因为FS3不是局部环，所以不可能是FS3/J(FS3)≅F2，因此FS3/J(FS3)≅F⊕F。

3)若|F|=pn，charF=P>3，则FS3为半单环，根据引理2知：

FS3≅M(n1,D1)⊕M(n2,D2)⊕…⊕M(nr,Dr)，

其中：Di是域F上的有限维除环，又F有限，所以Di是有限域，而且FS3是非交换的，那么至少存在一个i，使得ni>1，因为dimFZ(FS3)=3，所以FS3所有可能同构的情况如下：

FS3≅M(2,F)⊕F⊕F，

FS3≅M(2,F)⊕F2，

推论1设u(Z(FS3))是三次对称群S3在有限域F上群代数的单位群，V=1+J(FS3)，其中J(FS3)表示FS3的Jacobson根，则：

1)若|F|=2n，则u(FS3)/V≅GL(2,F)⊕F*。

2)若|F|=3n，则u(FS3)/V≅F*⊕F*。

3)若|F|=pn，charF=P>3，则u(FS3)≅GL(2,F)⊕F*⊕F*。

如果R是一个有限环，那么R/J(R)也是有限环，而在有限环中，u(R)=R-D(R)，由引理4知，x∈D(R)⟺x+J(R)∈D(R/J(R))，那么我们可以得出以下推论：

推论2设FS3为三次对称群S3在有限域F上的群代数，J(FS3)为FS3的Jacobson根，则：

1)若|F|=2n，则D(FS3)=∪(x+J(FS3))，

其中：

x+J(FS3)∈D(FS3/J(FS3))，D(FS3/J(FS3))≅D(M(2,F)⊕F)。

2)若|F|=3n，则D(FS3)=∪(x+J(FS3))，

其中：

x+J(FS3)∈D(FS3/J(FS3))，D(FS3/J(FS3))≅D(F⊕F)。

3)若|F|=2n，则D(FS3)≅D(M(2,F)⊕F⊕F)。

定理2设FD5为10阶二面体群D5在有限域F上的群代数，J(FD5)为FD5的Jacobson根，则：

1)若|F|=5n，则FD5/J(FD5)≅F⊕F，其中J(FD5)=△(D5,H)，H={1,a,a2,a3,a4}。

2)若|F|=pn，charF=p>3,5|(p-1)或n为偶数，则：

FD5≅M(2,F)⊕M(2,F)⊕F⊕F。

证明：(1)易验证H◁D5，且|D5/H|=2，那么charF†|D5/H|，根据引理1知：J(FD5)=△(D5,H).又根据引理3知：

{a-1,a2-1,a3-1,a4-1,b(a-1),

b(a2-1),b(a3-1),b(a4-1)}

为△(D5,H)在F上的一组基，所以△(D5,H)在F上的维数为8，即dimFJ(FD5)=8，那么dimFFD5/J(FD5)=2，从而FD5/J(FD5)只可能同构于以下两种形式：

FD5/J(FD5)≅F⊕F，FD5/J(FD5)≅F2。

又因为FD5不是局部环，所以不可能是FD5/J(FD5)≅F2，因此FS3/J(FD5)≅F⊕F。

3)若p为不等于2，5的素数，那么p†|D5|，所以FD5是一个半单环，根据引理2有：

FD5≅M(n1,D1)⊕M(n2,D2)⊕…⊕M(nr,Dr)，

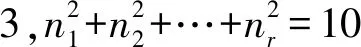
FD5≅M(2,F)⊕M(2,F)⊕F⊕F，

FD5≅M(2,F)⊕M(2,F)⊕F2，

FD5≅M(2,F2)⊕F⊕F，

FD5≅M(2,F2)⊕F2。

情况一：当5|(p-1)时，那么对所有的n:pn≡1(mod5)，则：

2）专题要素，土地用途区、土地现状用途、允许建设区、有条件建设区和重要产业项目与基础设施项目名称及布局；

情况二：当5†(p-1)且n为偶数时：

若a2p=a2，a3p=a3，则p≡1(mod5)，这与5†(p-1)矛盾。

若a2p=a3，a3p=a2，则2p≡3(mod5)，3p≡2(mod5)，从而p≡1(mod5)，这与5†(p-1)矛盾。

FD5≅M(2,F)⊕M(2,F)⊕F⊕F。

推论3设u(Z(FD5))是10阶二面体群D5在有限域F上群代数的单位群，V=1+J(FD5)，其中：J(FD5)表示FD5的Jacobson根，则：

1)若|F|=5n，则u(FD5)/V≅F*⊕F*，

2)若|F|=pn，charF=p>3,5|(p-1)或n为偶数，则：

u(FD5)≅GL(2,F)⊕GL(2,F)⊕F*⊕F*。

推论4设FD5为10阶二面体群D5在有限域F上的群代数，J(FD5)为FD5的Jacobson根，则：

1)若|F|=5n，则D(FD3)=∪(x+J(FD5))，

其中：

x+J(FD5)∈D(FD5/J(FD5))，

D(FD5/J(FD5))≅D(F⊕F)。

2)若|F|=pn，charF=p>3,5|(p-1)或n为偶数，则：

D(FD5)≅D(M(2,F)⊕M(2,F)⊕F⊕F)。