变宽截面箱梁剪力滞效应研究

卢敏锋， 丁南宏

(兰州交通大学 土木工程学院，兰州 730070)

1 引 言

受地形条件和交通的限制，横向变宽度桥梁运用越来越广泛，但变宽度箱梁的理论研究还较少。剪力滞是由于箱梁翼缘板的剪切变形不均匀，造成弯曲正应力沿梁宽方向不均匀分布的现象。文献[1]应用变分法分析了等截面箱梁的剪力滞效应，提出了分析简支箱梁及连续箱梁剪力滞效应的方法。文献[2,3]运用能量变分原理对多箱室等截面箱梁建立了相应的控制微分方程和边界条件。文献[4-7]应用能量变分法，分析了波形钢腹板组合箱梁的剪力滞效应，给出了计算组合箱梁剪力滞系数的解析方法。文献[8-12]分别考虑了梗腋、翼板厚度变化、悬臂板宽度以及腹板剪切变形等因素对箱形梁剪力滞的影响，运用能量变分原理导出了计算箱梁剪力滞效应的公式。文献[13]应用能量变分原理,对变高度梯形截面箱梁的剪力滞及剪切变形效应进行了分析，导出了箱梁在横向荷载作用下的剪力滞控制微分方程和边界条件，获得相应的闭合解。文献[14]用能量变分法分析了变宽截面波形钢腹板组合箱梁剪力滞，推导出了简支箱梁在均布荷载和集中荷载作用下剪力滞系数的计算公式。文献[14]为四箱单室箱梁，纵向位移函数为二次函数，未考虑顶板宽度变化对箱梁正应力的影响。文献[15]以等截面箱梁控制方程为基础，推导出变高度波形钢腹板箱梁的控制微分方程，应用差分法得到变高度箱梁的剪力滞系数计算公式。

上述文献主要针对等截面箱梁及变高度箱梁的剪力滞效应进行了研究。目前，对于变宽度箱梁剪力滞效应的研究较少，研究方法主要是有限元分析，且箱梁的结构形式和截面参数变化情况也不相同。本文以三次抛物线作为箱梁纵向翘曲位移的分布函数，应用能量变分原理，建立控制微分方程。考虑到顶板宽度沿梁的线性变化时截面参数I(x)和h(x)的变化以及对箱梁正应力的影响，采用差分法计算箱梁在集中荷载和均布荷载作用下的正应力，总结顶板变宽箱梁的剪力滞效应分布规律。

2 基本假定

(1) 中和轴仍位于按初等梁理论计算的位置。

(2) 腹板变形符合平截面假定，只考虑纵向弯曲变形势能，忽略横向弯曲变形势能。

(3) 翼缘板的竖向无挤压即εz=0，板平面外剪切变形γx z与γy z以及横向变形εy均忽略不计。

(4) 箱梁在竖向对称荷载作用下，翼板的纵向位移假设为

(1)

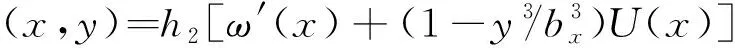
(2)

(3)

顶板宽度沿梁长的变化函数为

(4)

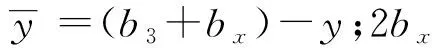
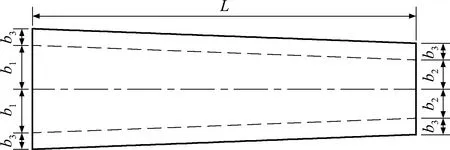
图1 变宽箱梁平面图

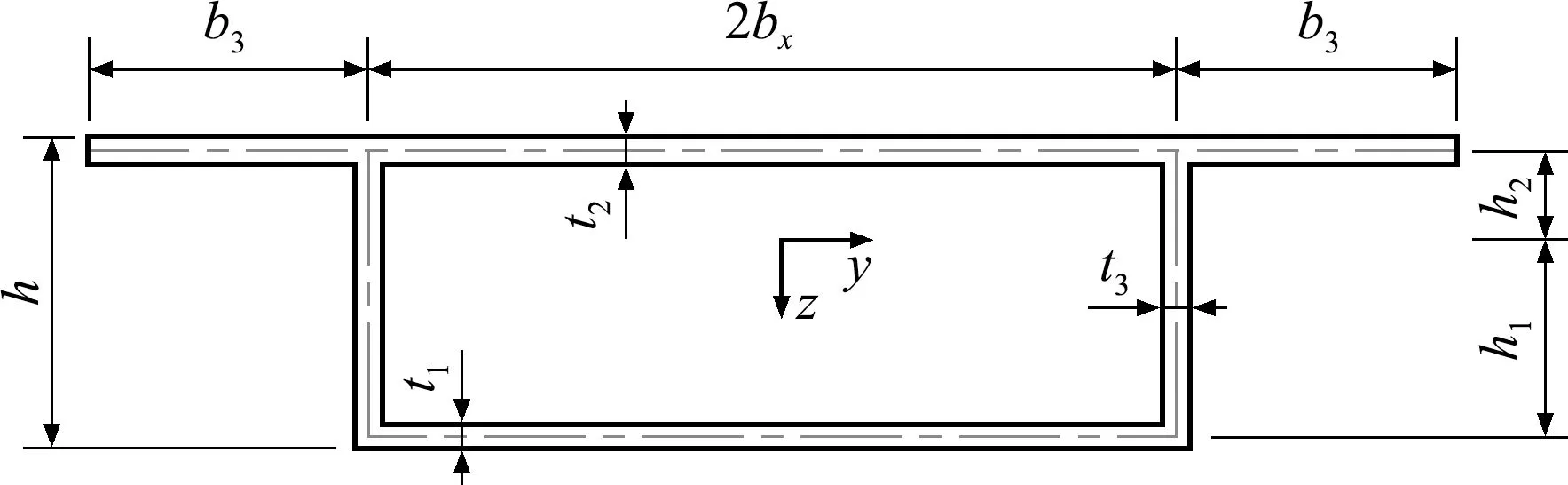
图2 箱梁横截面

3 变宽度箱梁控制微分方程及其解答

3.1 总势能表达式

当箱形梁弯曲时，外力势能

(5)

组成箱梁各板的应变能为

(6)

(7)

将式(1～3)分别代入式(6，7)得

底板应变能为

(8)

顶板应变能为

(9)

悬臂板应变能为

(10)

腹板应变能为

(11)

体系总势能为

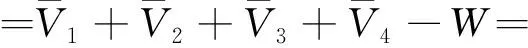
(12)

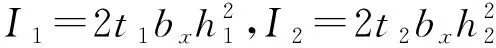
3.2 控制微分方程的建立

根据最小势能原理，在外力作用下结构处于平衡状态时，当有任何虚位移时，体系总势能的变分为零[1]。

(13)

将总势能变分，整理得控制微分方程为

(14)

(15)

边界条件为

(16)

当b1=b2=b3=b时，为等截面箱梁，即α=0，此时的剪力滞效应控制微分方程和边界条件退化为

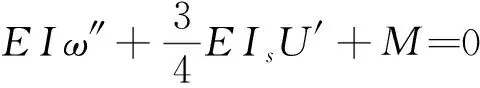
与文献[1]一样，说明本文方法具有一般性。

3.3 控制微分方程的求解

对式(14)两边求导，代入式(15)，移项整理得到关于剪切转角U(x)的方程为

(17)

将式(14)代入式(16)，可得边界条件

(18)

将式(17)中U″(x)的系数化为1，整理简化后为

(19)

底板正应力为

(20)

顶板正应力为

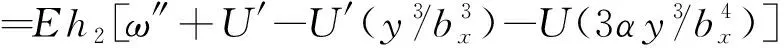
(21)

悬臂板正应力为

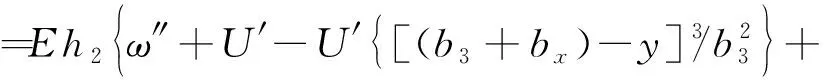
(22)

由于直接求解U(x)比较复杂，因此采用差分法来求解U(x)，沿梁长度方向划分网格，步长为λ，则点i纵向位移差函数U(x)的差分形式由文献[15,16]可知

(dU/dx)i=(Ui +1-Ui -1)/2λ

(d2U/dx2)i=(Ui +1-2Ui+Ui -1)/λ2

(23)

将式(23)代入式(19)整理后得

Ui -1(2-miλ)+Ui(-4+2λ2ki)+

Ui +1(2+miλ)=2λ2fi

(24)

式中fi=-ai[M/(EI)]′-di[M/(EI)]

边界条件的差分形式为

网格内的每一点利用式(24)列出方程，在边界点采用相应的边界条件，得到差分方程组，求解方程组得到变宽截面箱梁剪力滞效应纵向位移差函数U(x)，然后根据式(20～22)求出箱梁截面正应力。

4 算 例

已知简支钢箱梁的跨长L=30 m，其L/4位置和L/2位置截面尺寸如图3所示，材料特性为E=2.06×105MPa，G=0.79×105MPa，泊松比μ=0.31。(1) 在沿跨长腹板顶面，对称地作用均匀线荷载q=50 kN/m； (2) 在跨中腹板的顶面上对称地作用一对集中力2P=2×50 kN。计算在两种荷载作用下的箱梁截面应力。

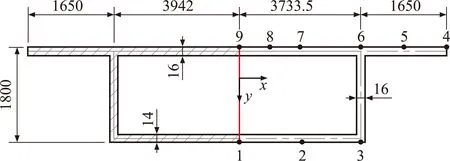
图3 箱梁L /4和L /2位置横截面(单位：mm)

利用有限元软件建立薄壁钢箱梁板壳单元模型，单元采用SHELL181单元。根据文献[16,17]可知，网格会对计算结果产生影响。因此需要对不规则的网格进行单独划分，以免影响结果的准确性。根据ANSYS模型得到应力结果列入表1和表2。

表1 均布荷载作用下简支箱梁截面应力(单位：MPa)

按变分法与有限元法计算在集中荷载和均布荷载作用下箱梁L/4和L/2位置截面应力，计算结果列入表1和表2，沿跨长腹板顶面应力如 图4 和图5所示。可以看出，变分法结果与有限元结果相吻合，表明本文的方法是可行的。但由于有限元法考虑的因素较多，网格划分以及差分法求解时，步长的选取也会对计算结果的精度产生影响，因此变分法的结果与有限元结果存在一定误差。

图4 均布荷载作用下变分解与有限元解

图5 集中荷载作用下变分解与有限元解

对变宽箱梁和等截面箱梁的跨中截面顶板进行比较，分析变宽箱梁和等截面箱梁的剪力滞分布差异。等截面梁的尺寸如图3(1/2横截面)所示，在相同荷载条件下等截面梁和变宽截面梁的跨中截面顶板应力分布如图6和图7所示，等截面简支箱梁的应力计算方法根据文献[1]得到。

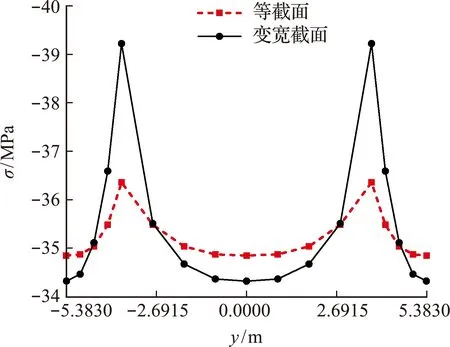
图6 均布荷载下跨中截面顶板应力(单位：MPa)

图7 集中荷载下跨中截面顶板应力(单位：MPa)

从图6可以看出，均布荷载作用下变宽度梁和等截面梁的跨中截面应力为正剪力滞分布；变宽箱梁与等截面腹板顶面应力相差约7.86%；变宽箱梁跨中截面的顶板应力分布变化较大，最大和最小应力相差14.25%。等截面梁最大和最小应力相差4.32%。由此可知，在均布荷载作用下，变宽截面的顶板应力变化幅度大，峰值更高，顶板的宽度变化对剪力滞效应影响比较大。

从图7可以看出，集中荷载作用下变宽度梁和等截面梁的跨中截面应力为正剪力滞分布。变宽箱梁与等截面腹板顶面应力相差0.099%，顶板中心应力相差2.69%，二者应力分布曲线拟合较好。由此可见，在集中荷载作用下，变宽度梁与等截面梁的顶板应力分布相似，在悬臂板端部和顶板中心略有差异，顶板的宽度变化对剪力滞效应影响较小。

5 结 论

(1) 当箱梁顶板、底板和悬臂板宽度沿跨长相等时，推导的剪力滞效应控制微分方程退化为等截面箱梁剪力滞效应控制微分方程，说明本文的方法具有一般性。应用能量法与有限元法计算结果相吻合，二者应力分布曲线拟合较好。

(2) 在均布荷载作用下，变宽箱梁和等截面箱梁跨中截面应力为正剪力滞分布，与等截面梁相比，变宽截面梁应力变化幅度更大，腹板顶面应力峰值也更高，宽度的变化对剪力滞影响较大。

(3) 在集中荷载作用下，变宽箱梁和等截面箱梁跨中截面应力为正剪力滞分布。二者应力分布曲线相似，在悬臂板端部和顶板中心略有差异，故箱梁宽度的变化对剪力滞的影响较小。