HLLE++格式在高马赫数空腔流动模拟中的应用

张培红， 罗 磊， 贾洪印， 赵 炜， 张耀冰， 吴晓军

(中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000)

1 引 言

空腔流动现象广泛存在于内埋武器舱、起落架舱和表面缝隙等航空飞行器工程实际中，由于其巨大的工程实际意义和流动的复杂性，长期以来受到广泛关注和研究[1]。特别是数值模拟方法的发展，为空腔流动的研究提供了新的强有力的工具和手段。相关的研究表明[2-5]，采用RANS方程进行数值模拟得到的结果，在空腔静态流动形态、底板中心线平均压力分布系数等方面与试验结果吻合较好。如早期采用MacCormack显式二步预估差分格式计算亚声速和超声速空腔流动[3]，以及采用Brailovskays差分算法[4]、三阶迎风TVD格式和隐式格式[5]等，都取得了很好的效果。

数值格式是数值求解的基础和灵魂，数值格式的发展，大大促进了数值模拟在空腔流动研究中的应用。Jameson等[6]提出了著名的JST格式，通过构造人工粘性很好地解决了激波附近的振荡问题。随后，迎风格式的研究极大推进了数值求解技术的发展，Godunov格式的提出[7]为迎风格式的发展提供了新的方向。特别是针对Godunov格式中求解Riemann问题计算量大的缺陷，Roe[8]提出了对激波和接触间断都有很好分辨率的近似Riemann求解器，更是把数值模拟的应用推向了巨大成功。Hamed等[9]采用三阶Roe格式，研究了马赫数1.19的空腔流动，得到了与实验数据较为一致的结果。Arunajatesan等[10]采用数值模拟方法研究了空腔不同长宽比的影响。

侯中喜等[11]采用高精度和高分辨率格式开展了超声速开式空腔流动特性研究。马明生等[12]通过求解可压缩流动，研究了不同L/D对空腔流动特性的影响，分析了空腔流动类型随L/D增大转变的机理。李晓东等[13]通过求解N-S方程，对亚音速空腔流动进行研究。肖虹等[14]利用求解雷诺平均N-S方程研究了飞行器腹部空腔绕流情况。文献[15，16]对亚、跨和超声速条件下空腔流场特性进行了较为深入系统的研究。

上述研究多是针对马赫数2以下的空腔流动开展研究，而对于马赫数大于2的高马赫数空腔流动研究较少。高马赫数空腔流动的强激波和强剪切的流动特点，对数值格式的数值精度和稳定性提出了更高的要求。HLLE++格式兼具了Roe格式的数值精度与HLLE+格式的稳定性，具有可在2个网格内捕捉到激波、无熵增、边界层耗散小、精确捕捉接触间断和可大大降低红玉现象的发生等优点。

本文结合非结构网格和HLLE++格式的特点，通过改进激波探测的求解，把HLLE++格式应用到高马赫数空腔流动的数值模拟中，有效解决了高马赫数空腔流动中激波捕捉和流动分离模拟对数值精度和稳定性的要求，取得了较好的效果，为开展高马赫数空腔流动研究提供了可靠手段。

2 HLLE++格式及其改进

HLL族格式是由Harten等[17]提出的一族Godunov格式，HLL格式用内部状态的平均值来简化单元界面处的Riemann问题解。最简单的HLL格式假设在最大左行波和右行波之间只有一个内部状态，如图1所示。Einfeldt[18]基于最简单的HLL格式假设，提出了HLLE格式。HLLE格式具有很好的鲁棒性，但存在扩散性过大和接触间断信息丢失的缺点。

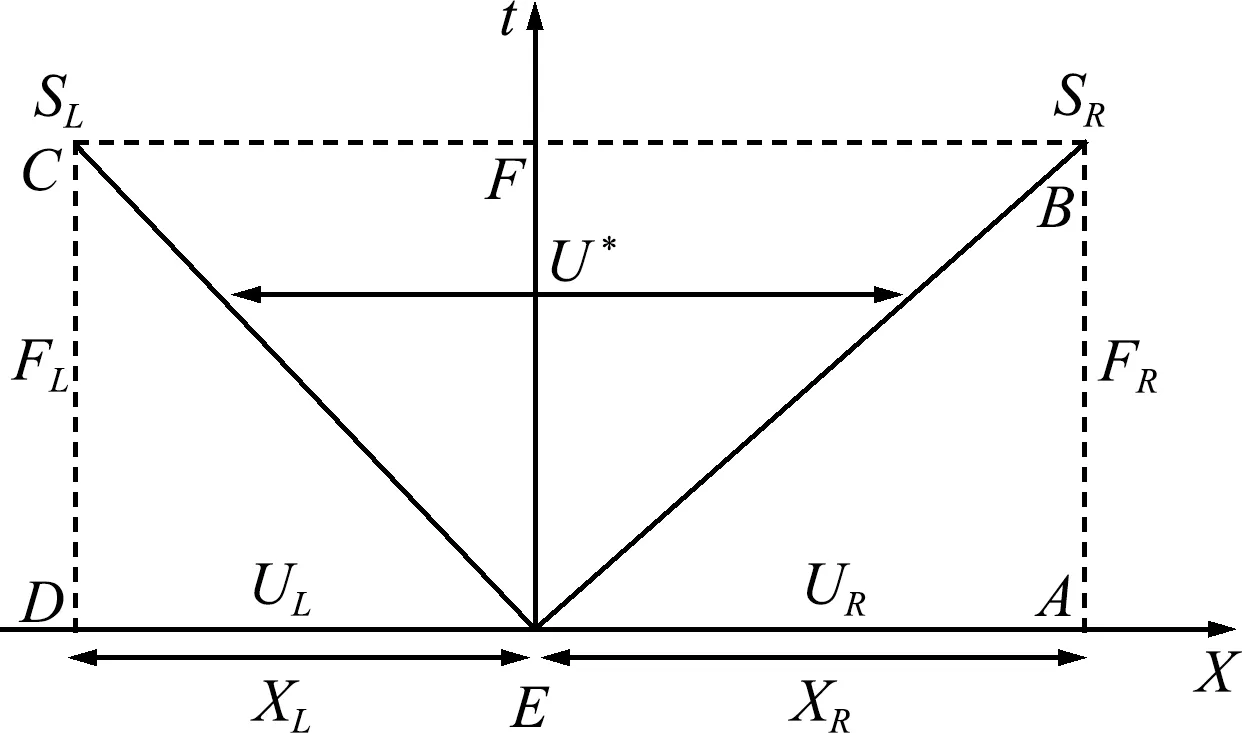
图1 HLL格式假设

针对HLLE格式的缺点，Einfeldt[18]在HLLE格式的基础上增加了针对线性特征场的反扩散项，发展了HLLEM格式。Park等[19]注意到利用 HLLEM 格式的形式，选择不同的波速和接触间断速度，可以分别得到HLLE，HLLEM和Roe格式，故提出结合HLLEM格式的波速判断和Roe格式的接触间断速度判断，形成了HLLE+格式。Tramel等[20]在HLLE+的基础上，采用新的开关函数，同时将特征值替换为HLLE+的特征值和Roe的耗散形式的特征值的混合组合形式，形成HLLE++格式，可表示为

(1)

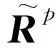
(2,3)

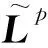
(4)

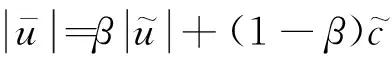
(5)

式中β为开关函数，

βHLLE + +=MAX(βHLLE + +, 0.4)

βHLLE + +=MIN(βNEW,C 1,βNEW,C 2)

(6)

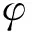
Swi,j,k=MAXl =i -1, i +1m =j -1, j +1n =k -1, k +1(kpl,m,n)

(7)

非结构网格不像结构网格那样具有明确的i,j和k三个方向[21，22]，式(7)的激波探测公式不再适用。本文针对非结构网格的特点，对激波探测的求解方式进行了改进，目的是最大可能地探测网格点i周围的激波单元，提高格式的数值精度和稳定性，可表示为

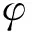
(8)

式中j为与单元i共点的所有单元，包括i自身。

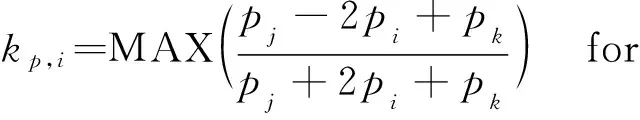
(9)

式中j和k为与单元i共面的单元。

δ为输入参数，取值范围为0～1，取值越小，格式耗散越大，稳定性越好，一般取为0.1。

3 HLLE++格式验证

为了验证HLLE++格式对高马赫数流动的模拟能力，以超声速无粘斜坡为算例，采用Roe，HLLC和HLLE++三种格式进行对比计算分析。无粘斜坡的计算条件为M=4.0，H=0 km，斜坡坡度为30°。图2给出了无粘斜坡计算网格。图3～图5分别给出了不同格式计算得到的密度云图。

图2 无粘斜坡计算网格

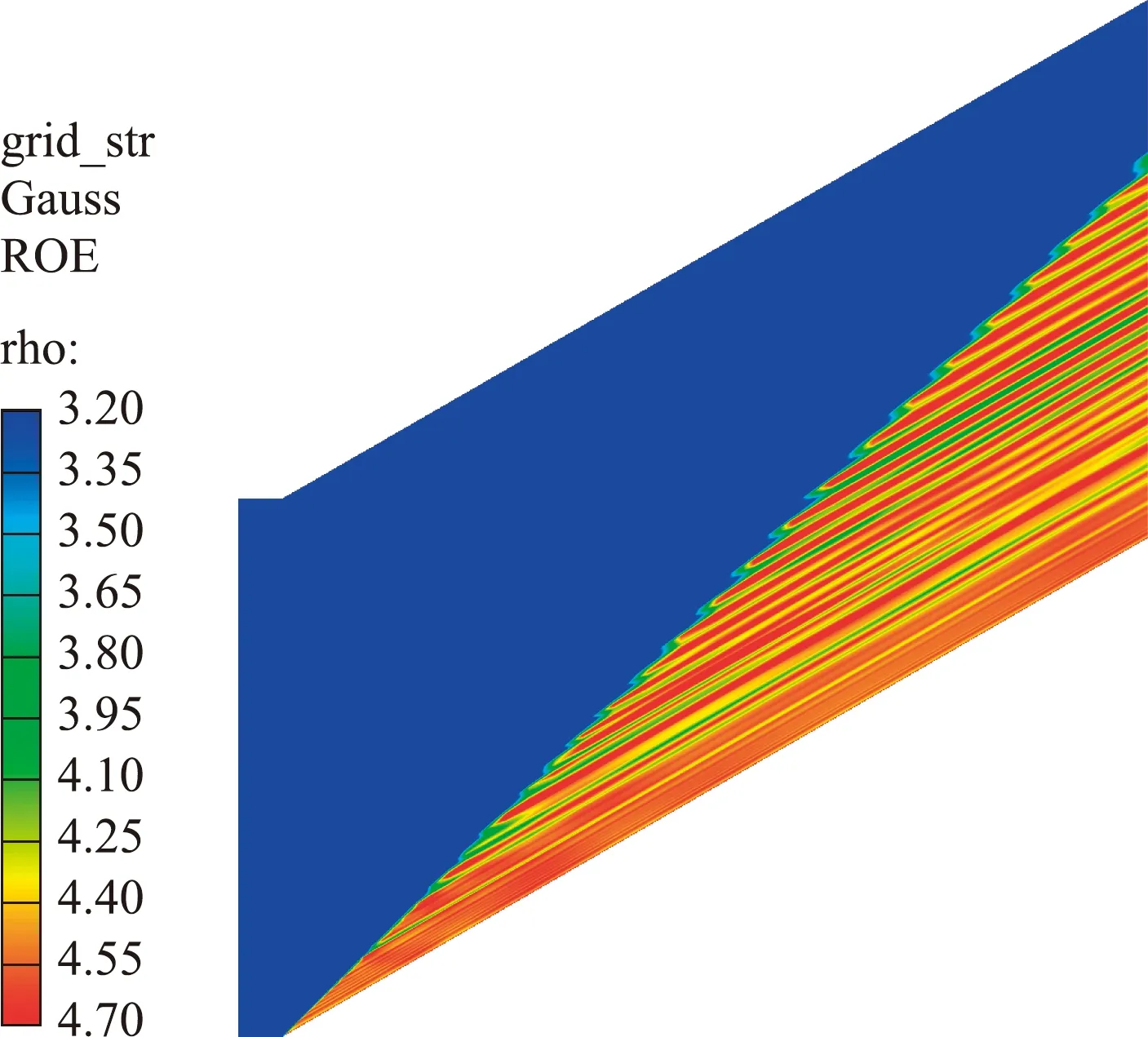
图3 Roe格式计算结果

图4 HLLC格式计算结果

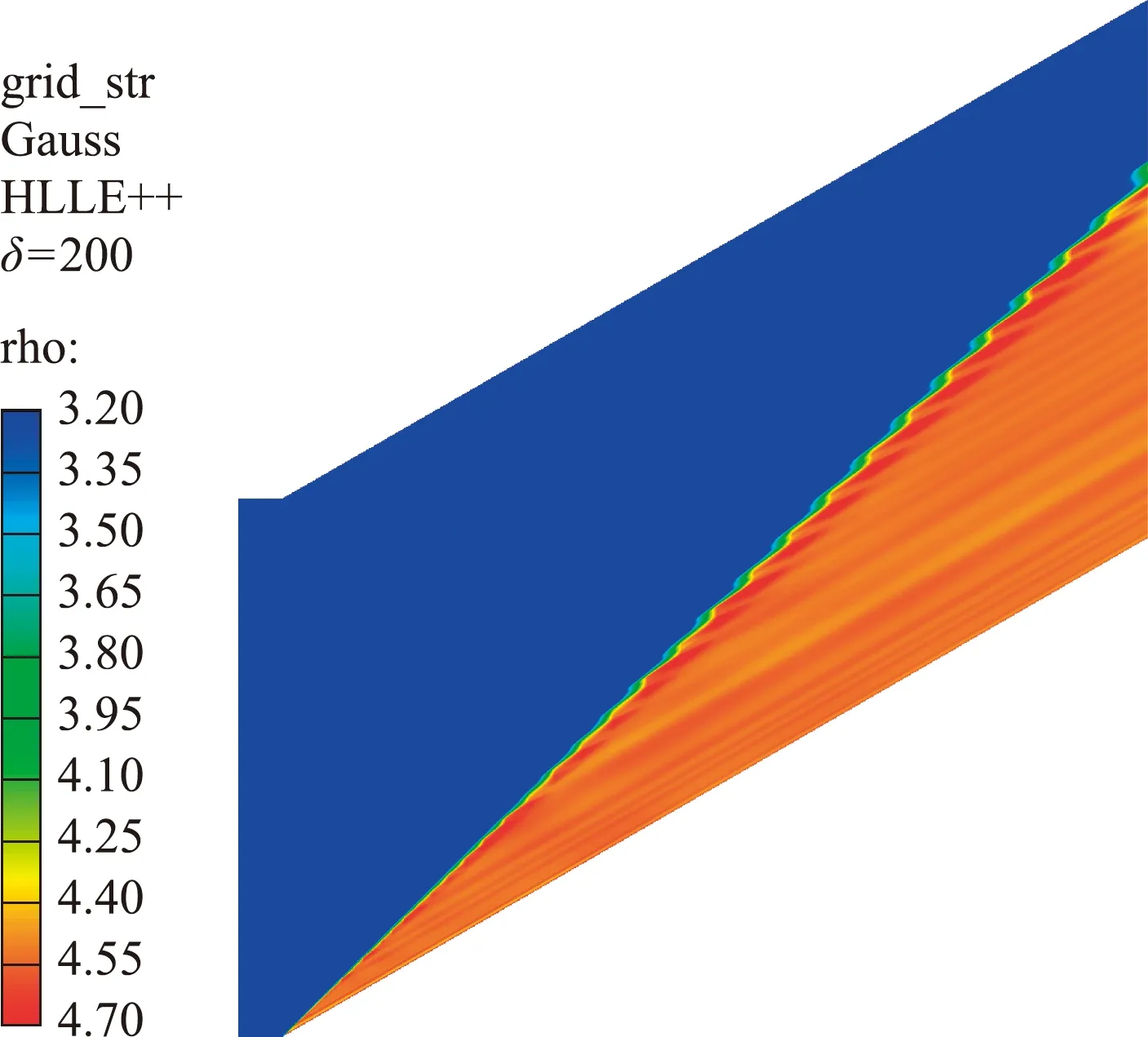
图5 HLLE++格式计算结果

可以看出，对于不是沿激波排列的网格，Roe格式和HLLC格式在斜坡超声速激波附近出现了明显的红玉现象，沿网格分布激波出现明显的台阶状，产生的误差传播到激波的下游。出现这种现象的原因是Roe和HLLC等近似Riemann解格式都是从一维流动推导而来，当推广到二维和三维时，会带来数值误差源。近似Riemann解格式对网格沿激波排列具有高度的敏感性，当网格没有沿激波排列时，在不同方向上的Riemann问题就会发生交叉耦合现象。穿过激波的守恒变量的强跳跃受Riemann求解器在非排列网格的各个方向上错误的表征为其他特征变量的强跳跃，对于具有数值耗散的格式，这将会带来格式的数值误差。由于其直接放大了单元界面的法向速度，如果单元面法向速度方向刚好是激波的切线方向，会导致本来很小的速度分量错误放大。而在单元界面的切向方向由于耗散的缺乏，造成交叉耦合扰动或者放大，或者保持中立稳定，即扰动无阻尼地传播。在这两种情况下，解的质量严重退化，就会产生非物理特性，通常称为红玉现象。HLLE++格式大大改善了这种缺陷，在捕捉高超声速激波时不会发生红玉现象，同时保持在光滑区域的低数值耗散特性。

为进一步验证HLLE++在边界层区域的低耗散特性和在激波捕捉时能够避免红玉现象发生的能力，采用本文数值方法模拟了高马赫数经典标准算例双椭球的流场和热流分布。双椭球模型为两个具有不同轴长的同心半椭球垂直相贯形成，后段接一等截面椭圆柱构型，模型全长215 mm，横向最大尺寸131.6 mm，最大高度105.3 mm。计算马赫数7.8，攻角0°，来流静温74.42 K，壁温296.0 K。计算时网格量为1322184，其中四面体539466，三棱柱777832，金字塔4886。物面网格为267582个三角形，附面层第一层为1.6×10-6m，对应网格雷诺数为45，增长率为1.2。图6给出了计算得到的双椭球对称面流场。可以看出座舱前的分离、再附和二次分离以及头部弓形激波、激波/激波干扰等流动特征得到很好的模拟，在头部激波附近未出现红玉现象。图7给出了计算得到的双椭球对称面中心线热流分布与试验比较。热流计算对数值方法在边界层区域的低耗散特性提出了更高要求，可以看出，计算值与试验值吻合较好，说明本文数值方法在边界层区域保持了低耗散特性。

图6 双椭球对称面流场

图7 双椭球对称面中心线热流分布

4 高马赫数空腔流动数值模拟

4.1 网格影响研究

为验证HLLE++格式模拟高马赫数空腔流动的可靠性和有效性，以文献[23]的空腔试验模型为算例，开展了数值模拟和网格影响研究。

该试验模型的空腔后壁板和侧壁板均可活动，用以调节空腔的长深比和长宽比，空腔前后壁板和底板上沿对称面布置了多个测压孔，如图8所示。本次计算采用的是长深比为24的空腔模型，空腔模型的主要几何参数和来流参数列入表1。

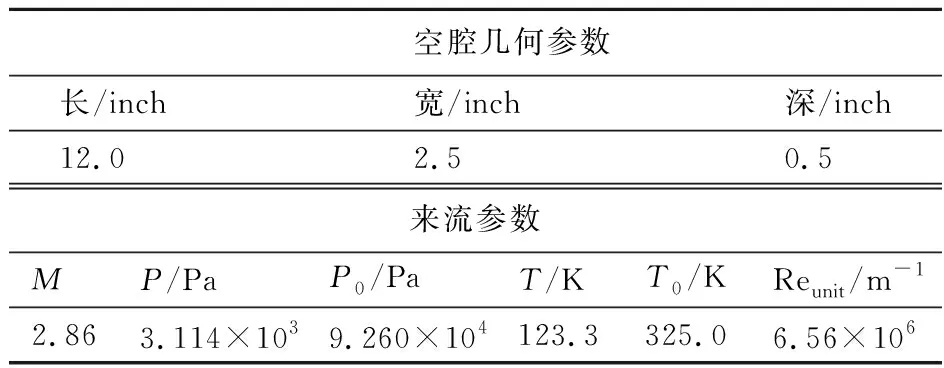
表1 空腔模型参数和来流参数

图8 空腔试验模型

计算网格是影响数值模拟精度的主要因素之一，只有网格分布合理和网格量足够时，模拟结果才会受网格影响较小或者与网格无关，因此数值模拟中通常会开展网格的无关性或网格的收敛性研究。本文采用4套网格由疏到密，网格量分别约为400万、1000万、2400万和4200万，并按此顺序分别命名为Grid1,Grid2,Grid3和Grid4。网格划分采用非结构的四面体+三棱柱+六面体单元的混合网格策略，在空腔内全部使用六面体(矩形)单元以保证较好的正交性，空腔外为混合网格单元。图9 给出了Grid3的对称面网格。计算时，无粘通量采用HLLE++格式离散，湍流模型采用k-ωSST两方程模型。

图9 空腔对称面网格

图10给出了4套网格的残值收敛曲线。可以看出，四套网格计算收敛都很好，残差下降5个量级以上。图11给出了不同网格计算得到的对称面上空腔底部、前缘平板和后缘平板上的压力系数分布与试验结果比较。图12给出了不同网格计算得到的对称面上空腔前壁板和后壁板上的压力系数分布与试验结果比较。其中，FP,RP,FL,FF和RF分别指空腔前缘平板、空腔后缘平板、空腔底板、空腔前壁板和空腔后壁板上的试验测量结果。

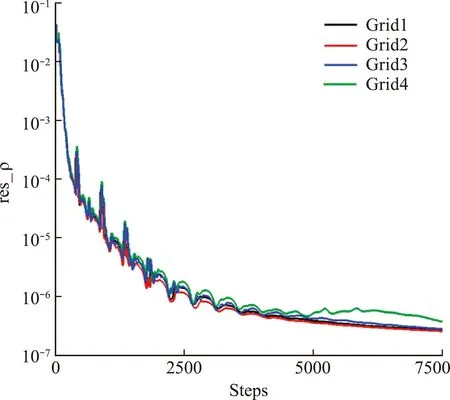
图10 不同网格残差收敛曲线

从图11和图12可以看出，对于上述4套网格，空腔上游流动、前壁板分离流动和两激波间附着平行流动处的模拟结果与试验符合较好。数值计算结果与试验结果的差异主要体现在后壁板分离流动和空腔下游流动的预测上。从图11可以看出，数值计算预测的后壁板分离流动在底板上的分离点位置相比于试验靠前，且网格越粗预测的分离点位置越靠前，与试验值偏离越远；随网格不断加密，分离点位置逐渐向后移动，靠向试验值；可以看出，对于较密的两套网格Grid3和Grid4，其计算结果几乎没有差别，但分离点位置与试验值相比仍有差异，这也导致了后壁板分离涡处空腔底板以及空腔后缘平板上的压力系数分布与试验存在一定差异。图12的结果同样表明，空腔后壁板上压力分布的预测结果随着网格加密逐渐接近试验结果，但网格加密到一定程度后，计算结果不再变化，且与试验结果存在一定差异。上述不同疏密网格的计算结果表明，本文采用的数值计算方法具有网格收敛性，空间离散误差随着网格加密迅速降低。同时，说明本文建立的HLLE++方法可以较好地模拟高马赫数空腔流动。

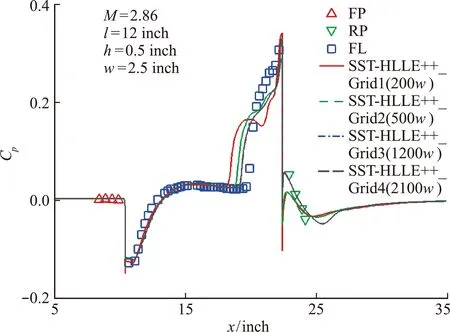
图11 不同网格对空腔对称面压力分布影响

图12 不同网格对空腔前后壁压力分布影响

4.2 湍流模型影响研究

对于激波、剪切层和大分离涡之间具有显著相互作用的高马赫数空腔流动而言，湍流模型会对数值模拟结果产生较为明显的影响。基于4.1节的空腔算例，考察了工程中常用的S -A一方程湍流模型和Menter的k-ωSST两方程湍流模型对模拟结果的影响。计算时网格采用Grid3网格。

图13和图14给出了S -A一方程模型和k-ωSST两方程模型的计算结果对比。可以看出，两种湍流模型对于空腔后台阶(前壁板)处分离涡尺度的模拟结果和对空腔内两分离涡之间的压力平台模拟结果基本一致，均与试验值符合较好。对于空腔前台阶(后壁板)处的分离流动，两种模型对分离点位置的预测差异不大；分离点后两种湍流模型计算结果，特别是后壁板附近底部压力分布差异较大，SST模型的计算结果与试验值更接近，而S -A模型的计算结果明显高于试验值。这说明两种湍流模型对空腔前台阶处分离区流动的计算结果存在明显差异。

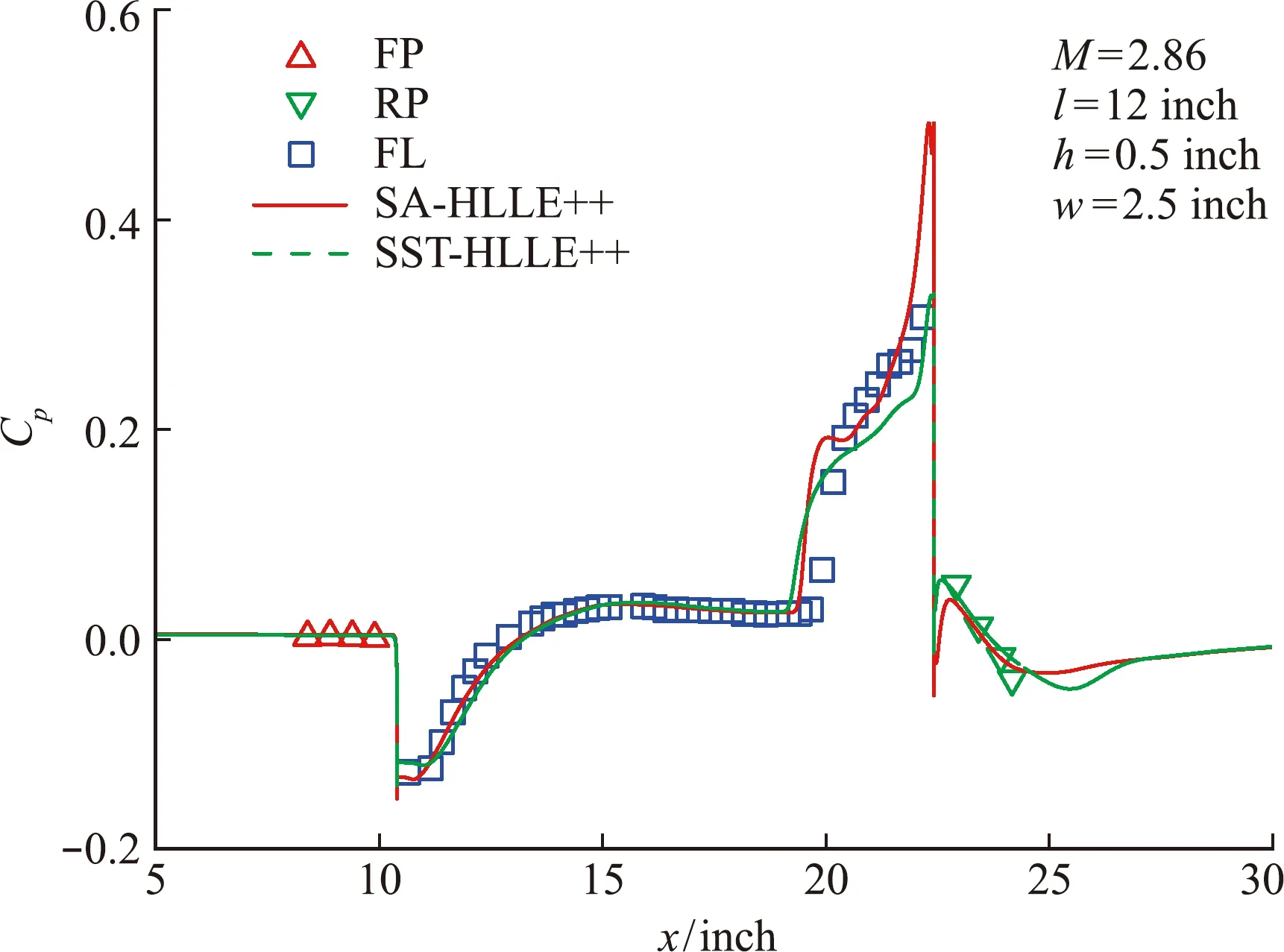
图13 不同湍流模型对空腔对称面压力分布影响

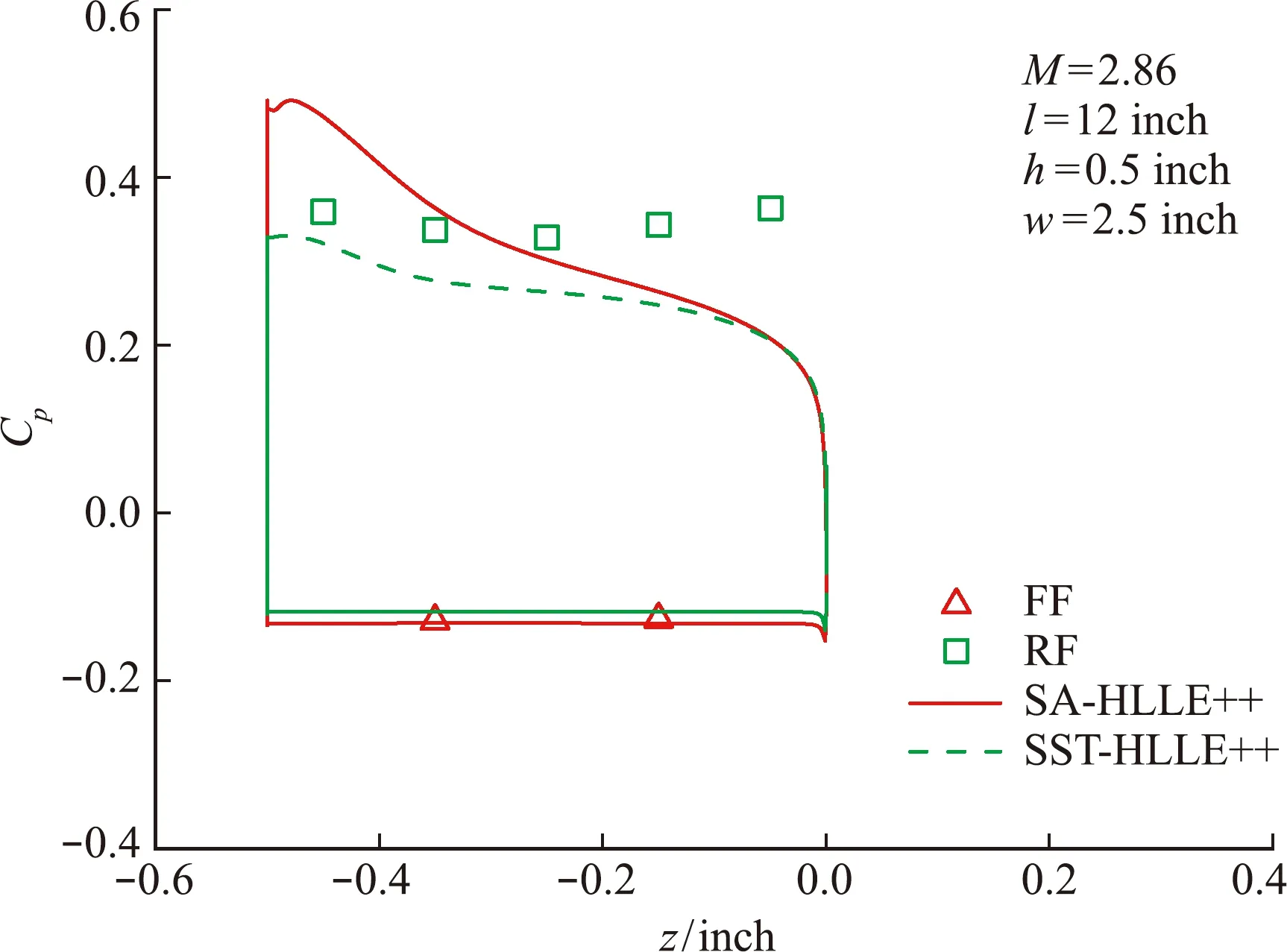
图14 不同湍流模型对空腔前后壁压力分布影响

图15～图17分别给出了两种湍流模型计算得到的空腔对称面压力系数云图、马赫数云图和总压恢复系数云图。其中，总压恢复系数定义为当地总压与来流总压之比。通过对比发现S -A模型计算的空腔前台阶(后壁板)处的分离涡尺度要明显大于SST模型的计算结果，主要体现在方向z上分离涡高度，S -A模型计算结果明显大于SST模型计算结果。同时可以注意到，S -A模型计算的剪切层厚度要明显大于SST模型，这对空腔外流动的影响表现为激波后总压恢复系数存在一定差异。由此可以看出，湍流模型主要影响的是剪切流动的计算结果，具体体现在剪切层/边界层厚度、分离区尺度和剪切输运效果的差异上，这些差异又同时导致了空腔外的流动状态，如激波强度和压缩/膨胀波传播角度等存在差异。结合图13和图14压力系数对比结果，可以看出，k-ωSST两方程湍流模型在对高马赫数流动问题的模拟上，相比于S -A模型更加接近真实流动情况。

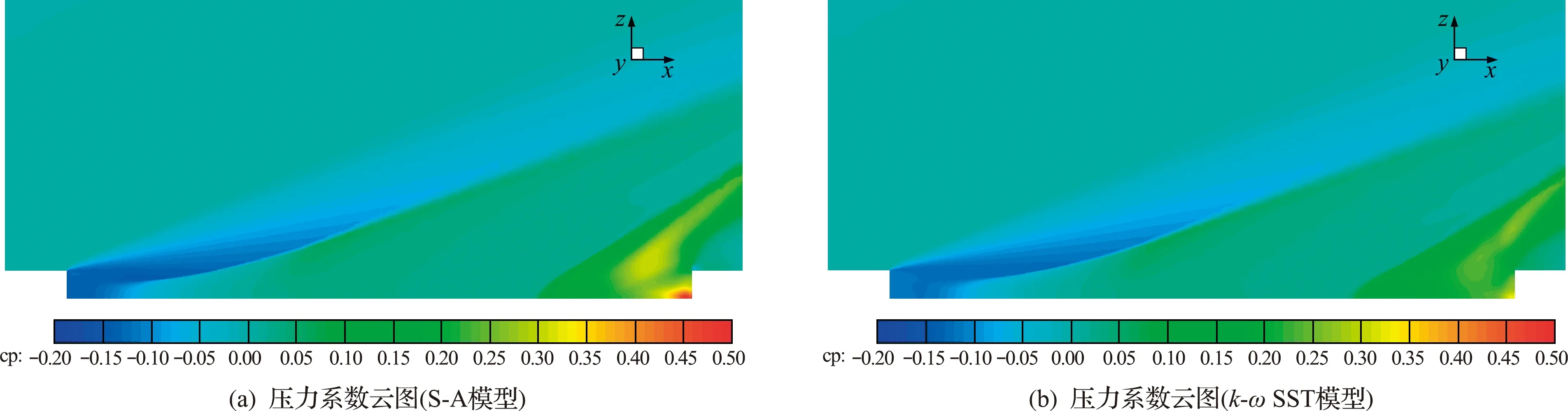
图15 不同湍流模型得到的压力云图比较

图16 不同湍流模型得到的马赫数云图比较

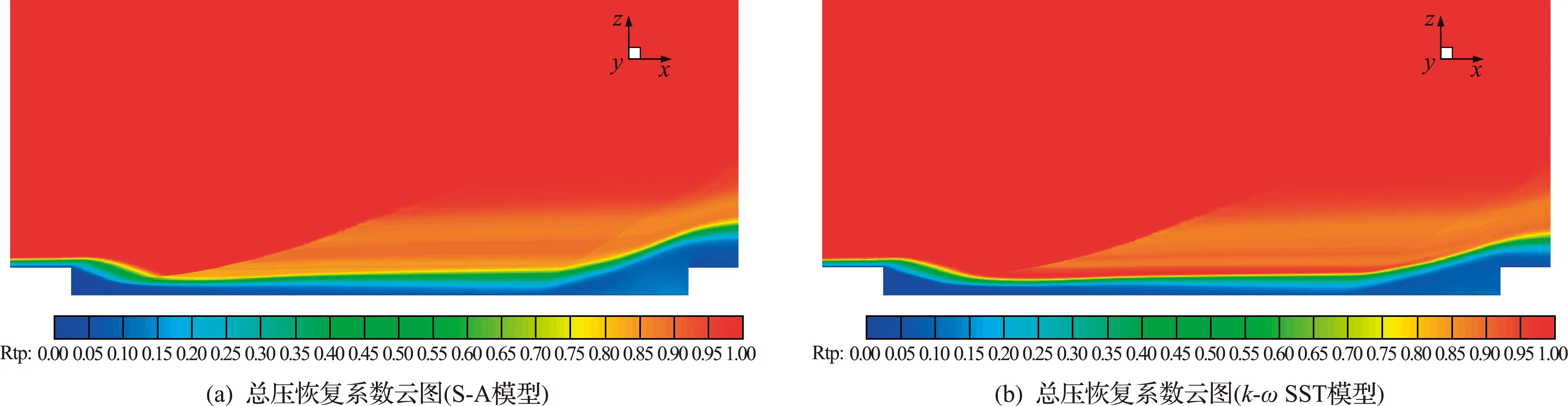
图17 不同湍流模型得到的总压恢复系数云图比较

5 结 论

针对非结构混合网格，通过改进激波探测的求解方法，建立了基于非结构混合网格的HLLE++计算方法，并应用于高马赫数空腔流动的模拟，可以得到以下结论。

(1) HLLE++格式在边界层区域可以较好地保持低数值耗散特性，在捕捉高超声速激波时可以有效避免红玉现象的发生。

(2) HLLE++格式可以较好地模拟高马赫数空腔流动特性，数值计算方法具有网格收敛性。

(3)k-ωSST两方程湍流模型在对高马赫数流动问题的模拟上，相比于S -A模型更加接近真实流动情况。